15.2: Косети та групи факторів

Last updated
Save as PDF

Page ID: 65070

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Розглянемо групу$\left[\mathbb{Z}_{12};+_{12}\right]\text{.}$ Як ми бачили в попередньому розділі, ми можемо зобразити її циклічні властивості за допомогою string art рисунка 15.1.1. Тут нас будуть цікавити негенератори, як 3. Суцільні лінії$\PageIndex{1}$ на малюнку показують, що лише третина прихватки були досягнуті, починаючи з нуля і стрибнувши до кожної третьої прихватки. Цифри цих прихваток відповідають$\langle 3 \rangle = \{0, 3, 6, 9\}\text{.}$

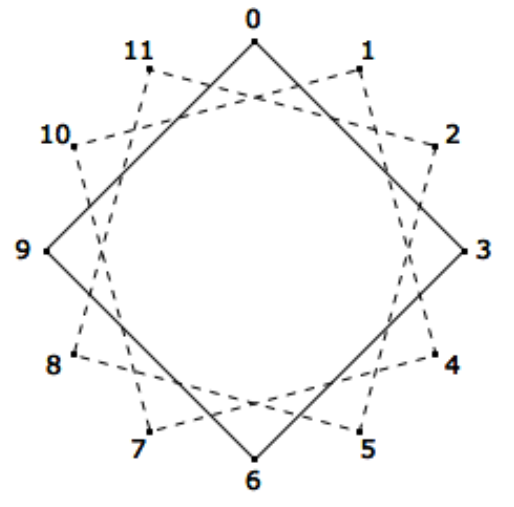$clipboard_e0957551dd6fd9f8cedb5b262f24867f8.png$ Малюнок$\PageIndex{1}$: Косети «Струнний арт»

Що станеться, якщо почати з однієї з невикористаних прихваток і знову перестрибнути на кожну третю прихватку? Два розбиті шляхи на малюнку$\PageIndex{1}$ показують, що утворюються однакові квадрати. Таким чином, прив'язки розділені на дуже схожі підмножини. Підмножини$\mathbb{Z}_{12}$, яким вони відповідають, є$\{0, 3, 6, 9\}\text{,}$$\{1, 4, 7, 10\}\text{,}$ і$\{2, 5, 8, 11\}\text{.}$ Ці підмножини називаються косетами. Зокрема, вони називаються косетами підгрупи.$\{0, 3, 6, 9\}\text{.}$ Ми побачимо, що за певних умов, косети підгрупи можуть утворювати власну групу. Перш ніж продовжувати цей приклад далі, ми розглянемо загальну ситуацію.

Визначення $\PageIndex{1}$: Coset

Якщо$[G;*]$ є групою,$H \leq G$ а$a \in G\text{,}$ лівою косетою, що$H$ генерується,$a$ є

\ begin {рівняння*} a*h =\ {a*h | h\ in H\}\ end {рівняння*}

і правильна косет$H$ генерується$a$ є

\ begin {рівняння*} h*a =\ {h*a | h\ in H\}. \ end {рівняння*}

Примітка$\PageIndex{1}$

$H$сама по собі є як лівою, так і правою косетами, оскільки$e*H = H*e = H\text{.}$
Якщо$G$ є абелівським,$a*H = H*a$ а ліво-праворуч різниця для косетів може бути скинута. Зазвичай ми будемо використовувати позначення лівої косети в цій ситуації.

Визначення$\PageIndex{2}$: Cost Representative

Будь-який елемент косети називається представником тієї косети.

Можна задатися питанням, чи$a$ є якимось чином спеціальний представник,$a*H$ оскільки він, здається, визначає косет. Це не так, як ми побачимо.

Зауваження$\PageIndex{1}$: A Duality Principle

Принцип подвійності може бути сформульований щодо косетів, оскільки ліва та права косети визначаються подібними способами. Будь-яка теорема про ліву і праву косети дасть другу теорему, коли «лівий» і «правий» обмінюються на «правий» і «лівий».

Теорема$\PageIndex{1}$

Якщо$b\in a*H\text{,}$ то$a*H = b*H\text{,}$ і якщо$b \in H*a\text{,}$ тоді$H*a = H*b\text{.}$

Доказ

У світлі наведеного вище зауваження нам потрібно лише довести першу частину цієї теореми. Припустимо, що$x \in a*H\text{.}$ Нам потрібно лише знайти спосіб вираження$x$ як «$b$часи елемент$H\text{.}$» Тоді ми доведемо це$a*H \subseteq b*H\text{.}$ За визначенням$a*H\text{,}$ так$b$ і$x$ є$a*H\text{,}$ там,$h_1$ і$h_2$ в$H$ таких що$b = a*h_1$ і$x = a*h_2\text{.}$ задано ці два рівняння,$a = b h_1^{-1}$ і

\ begin {рівняння*} x = a*h_2 = (b*h_1^ {-1}) *h_2 = b* (h_1^ {-1} *h_2)\ end {рівняння*}

Так як$h_1,h_2 \in H\text{,}$$h_1^{-1}*h_2 \in H\text{,}$ і ми закінчили з цією частиною доказу. Для того, щоб показати, що$b*H \subseteq a*H\text{,}$ можна виконати по суті ті ж кроки, які ми дозволимо читачеві заповнити.

Приклад$\PageIndex{1}$

На малюнку$\PageIndex{1}$ ви можете почати з 1 або 7 і отримати той самий шлях, роблячи стрибки по три прихватки на кожному кроці. Таким чином,

\ begin {рівняння*} 1+_ {12}\ {0, 3, 6, 9\} = 7 +_ {12}\ {0, 3, 6, 9\} =\ {1, 4, 7, 10\}. \ end {рівняння*}

Набір лівих (або правих) косетів підгрупи розділити групу особливим чином:

Теорема$\PageIndex{2}$: Cosets Partition a Group

Якщо$[G; *]$ є групою, а$H\leq G\text{,}$ набір лівих косет$H$ є розділом$G\text{.}$ Крім того, всі ліві косети$H$ мають однакову кардинальність. Те ж саме стосується правильних косетів.

Доказ

Те, що кожен елемент$G$ належить до лівої косети, зрозуміло, тому що$a \in a*H$ для всіх$a \in G\text{.}$ If$a*H$ і$b*H$ є left cosets, ми доведемо, що вони або рівні, або неспільні. Якщо$a*H$ і не$b*H$ є нероз'єднаними,$a*H\cap b*H$ є непорожнім, а якийсь елемент$c \in G$ належить до перетину. Тоді за теоремою$\PageIndex{1}$,$c\in a*H \Rightarrow a*H = c*H$ а$c \in b*H \Rightarrow b*H = c*H\text{.}$ звідси$a*H = b*H\text{.}$

Ми завершуємо доказ, показуючи, що кожен лівий косет має таку ж кардинальність, як$H\text{.}$ Для цього ми просто спостерігаємо, що якщо$a \in G\text{,}$$\rho:H \to a*H$ визначено$\rho(h)= a*h$ це біекція, і, отже,$\lvert H\rvert =\lvert a *H\rvert\text{.}$ Ми залишимо доказ цього твердження читачеві.

Функція$\rho$ має приємну інтерпретацію з точки зору нашого вступного прикладу. Якщо$a \in \mathbb{Z}_{12}\text{,}$ графік повернуто$\{0, 3, 6, 9\}$ так,$(30a)^{\circ}$ щоб збігатися з однією з трьох косет$\{0, 3, 6, 9\}\text{.}$

Слідство$\PageIndex{1}$: A Coset Counting Formula

Якщо$\lvert G\rvert < \infty$ і$H\leq G\text{,}$ кількість різних лівих косет$H$ дорівнює З цієї причини ми використовуємо$\frac{\lvert G\rvert }{\lvert H\rvert }\text{.}$ для$G/H$ позначення множини лівих косет$H$ in$G$

Доказ: Це випливає з$G$ поділу на однакові за розміром набори, одним з яких є$H\text{.}$

Приклад$\PageIndex{2}$

Множина цілих чисел, кратних чотирьом,$4\mathbb{Z}\text{,}$ є підгрупою з$[\mathbb{Z}; +]\text{.}$ Чотири різних косет$4\mathbb{Z}$ розділення цілих чисел. Вони є$4\mathbb{Z}\text{,}$$1+4\mathbb{Z}\text{,}$$2+4\mathbb{Z}\text{,}$ і$3+4\mathbb{Z}\text{,}$ де, наприклад, також$1+4\mathbb{Z} = \{1+4k | k \in \mathbb{Z}\}\text{.}$$4\mathbb{Z}$ можуть бути написані$0+4\mathbb{Z}\text{.}$

Конвенція$\PageIndex{1}$: Distinguished Representatives

Хоча ми і бачили, що будь-який представник може описати косету, часто зручно вибрати відмінного представника з кожної косети. Перевага цього полягає в тому, що для кожної косети існує унікальна назва з точки зору її видатного представника. У числових прикладах, таких як наведений вище, видатний представник, як правило, є найменшим ненегативним представником. Пам'ятайте, це чисто зручність і немає абсолютно нічого поганого в письмовій формі$-203+4\mathbb{Z}\text{,}$$5+4\mathbb{Z}\text{,}$ або$621+4\mathbb{Z}$ замість$1+4\mathbb{Z}$ тому, що$-203, 5, 621 \in 1+4\mathbb{Z}\text{.}$

Перш ніж завершити основну спрямованість цього розділу, відзначимо значний підтекст теореми$\PageIndex{2}$. Оскільки скінченна група ділиться на косети загального розміру будь-якою підгрупою, можна зробити висновок:

Теорема$\PageIndex{3}$: Lagrange's Theorem

Порядок підгрупи скінченної групи повинен ділити порядок групи.

Одне з безпосередніх наслідків теореми Лагранжа полягає в тому, що якщо$p$ є простим, не$\mathbb{Z}_p$ має належних підгруп.

Зараз ми опишемо операцію на косетах, яка за певних обставин призведе до групи. Для більшої частини цього розділу ми будемо вважати, що$G$ це абелінова група. Це одне достатнє (але не обов'язкове) умова, яке гарантує, що набір лівих косет сформує групу.

Визначення$\PageIndex{3}$: Operation on Cosets

Дозволяти$C$ і$D$ бути залишені$H\text{,}$ косети підгрупи$G$ з представниками$c$ і$d\text{,}$ відповідно. Тоді

\ begin {рівняння*} C\ otimes D = (C*h)\ час (D*h) = (c*d) * H\ end {рівняння*}

Операція$\otimes$ називається операцією, індукованою на лівих косетах шляхом$*\text{.}$

У$\PageIndex{4}$ теоремі пізніше в цьому розділі ми доведемо, що якщо$G$ це абелева група,$\otimes$ це дійсно операція. На практиці, якщо група$G$ є адитивною групою, символ$\otimes$ замінюється на такий,$+\text{,}$ як у наступному прикладі.

Приклад$\PageIndex{3}$: Computing with Cosets of $4\mathbb{Z}$

Розглянемо косети, описані в прикладі$\PageIndex{2}$. Для стислості, ми перейменуємо$0+4\mathbb{Z}\text{,}$$1+4\mathbb{Z}\text{,}$$2+4\mathbb{Z}\text{,}$$\bar{0}\text{,}$$\bar{1}\text{,}$$\bar{2}\text{,}$ і$3+4\mathbb{Z}$ з символами і$\bar{3}\text{.}$ Давайте зробимо типовий розрахунок,$\bar{1}+\bar{3}\text{.}$ Ми побачимо, що результат завжди буде$\bar{0}$, незалежно від того, які представники ми вибираємо. Наприклад,$9 \in \bar{1}\text{,}$$7\in \bar{3}\text{,}$ і$9+7=16 \in \bar{0}\text{.}$ наш вибір представників$\bar{1}$ і$\bar{3}$ був абсолютно умовним.

Взагалі, обчислити$C \otimes D$ можна різними способами, і тому необхідно показати, що вибір представників ніяк не впливає на результат. Коли результат, який ми отримуємо,$C \otimes D$ завжди не залежить від нашого вибору представників, ми говоримо,$\otimes$ що «чітко визначено». Додавання косет - це чітко визначена операція на лівих косетах 4$\mathbb{Z}$ і зведена в наступній таблиці. Ви помічаєте щось знайоме?

\ begin {рівняння*}\ begin {масив} {c|cccc}\ otimes &\ бар {0} &\ бар {1} &\ бар {2} &\ бар {3}\\ hline\ бар {0} &\ бар {1} &\ бар {2} &\ бар {3}\\ бар {1} &\ бар {1}\ бар {1} &\ бар {1} & бар {2} &\ бар {3} &\ бар {0}\\ бар {2} &\ бар {2} &\ бар {3} &\ бар {0} &\ бар {1}\\\ бар {3} &\ bar {3} &\ bar {0} &\ bar {1} &\ бар {2}\\ кінець {масив}\ кінець {рівняння*}

Приклад$\PageIndex{4}$: Cosets of the Integers in the Group of Real Numbers

Розглянемо групу дійсних чисел$[\mathbb{R}; +]\text{,}$ та її підгрупу цілих чисел,$\mathbb{Z}\text{.}$ Кожен елемент$\mathbb{R}/\mathbb{Z}$ має ту ж кардинальність, що і$\mathbb{Z}\text{.}$ нехай$s, t\in \mathbb{R}\text{.}$$s\in t+\mathbb{Z}$ якщо$s$ може бути записана$t+n$ для деяких$n \in \mathbb{Z}\text{.}$ Отже$s$ і$t$ належать до тієї ж косети, якщо вони відрізняються цілим числом. (Див. Вправа$\PageIndex{6}$ для узагальнення цього факту.)

Тепер розглянемо косет$0.25+\mathbb{Z}\text{.}$ Реальні числа, які відрізняються цілим числом від 0,25 є$1.25, 2.25, 3.25, \ldots$ і$-0.75, -1.75, -2.75, \ldots\text{.}$ Якщо вибрано будь-яке дійсне число, існує представник його косети, який більше або дорівнює 0 і менше 1. Цього представника ми назвемо шановним представником косети. Наприклад, 43.125 належить до косети, представленої 0,125;$-6.382+\mathbb{Z}$ має 0,618 як свого видатного представника. Операцію на$\mathbb{R}/\mathbb{Z}$ прийнято називати додавання по модулю 1. Кілька типових розрахунків$\mathbb{R}/\mathbb{Z}$ в

\ begin {рівняння*}\ почати {масив} {c} (0.1+\ mathbb {Z}) + (0.48+\ mathbb {Z}) = 0.58+\ mathbb {Z}\ (0.7+\ mathbb {Z}) + (0.31+\ mathbb {Z}) = 0.01+\ mathbb {Z}\ - (0.01+\ mathbb {Z} 41+\ mathbb {Z}) = -0.41+\ mathbb {Z} = 0.59+\ mathbb {Z}\\ textrm {і взагалі,} - (a+\ mathbb {Z}) = (1 - a) +\ mathbb {Z}\ end {масив}\ текст {.} \ end {рівняння*}

Приклад$\PageIndex{5}$: Cosets in a Direct Product

Розглянемо,$F = (\mathbb{Z}_4\times \mathbb{Z}_2 )/H\text{,}$ де$H=\{(0,0),(0,1)\}\text{.}$$\mathbb{Z}_4 \times \mathbb{Z}_2$ Since має порядок 8, кожен елемент$F$ - це косет, що містить дві впорядковані пари. Ми залишимо це читачеві, щоб переконатися, що чотири різні косети є$(0, 0)+H\text{,}$$(1,0) +H\text{,}$$(2, 0)+H$ і$(3, 0)+H\text{.}$ Читач також може перевірити, що$F$ є ізоморфним$\mathbb{Z}_4$, оскільки$F$ є циклічним. Освічена здогадка повинна дати вам генератор.

Приклад$\PageIndex{6}$

Розглянемо групу$\mathbb{Z}_2{}^4 = \mathbb{Z}_2\times \mathbb{Z}_2\times \mathbb{Z}_2\times \mathbb{Z}_2$. $H$$\langle (1,0,1, 0)\rangle\text{,}$Дозволяти циклічну підгрупу$\mathbb{Z}_2{}^4$ генерувати по (1,0,1,0). Так як

\ begin {рівняння*} (1,0,1, 0) + (1,0,1, 0) = (1+_21,0+_20,1+_21,0+_20) = (0,0,0,0)\ end {рівняння*}

порядок$H$ дорівнює 2 і,$\mathbb{Z}_2{}^4/H$ має$\lvert \mathbb{Z}_2^4 /H\rvert =\frac{\lvert \mathbb{Z}_2^4\rvert }{\lvert H\rvert }=\frac{16}{2}= 8$ елементи. Типовою косетою є

\ почати {рівняння*} C = (0, 1, 1, 1) +H =\ {(0, 1, 1, 1), (1, 1, 0, 1)\}\ кінець {рівняння*}

Зауважимо, що оскільки$2(0, 1, 1, 1) = (0, 0, 0, 0)\text{,}$$2C = C\otimes C = H\text{,}$ тотожністю для операції на$\mathbb{Z}_2{}^4/H\text{.}$ порядках неідентичних елементів цієї групи факторів є все 2, і можна показати, що група факторів ізоморфна до$\mathbb{Z}_2{}^3\text{.}$

Теорема $\PageIndex{4}$: Coset Operation is Well-Defined (Abelian Case)

Якщо$G$ є абелевою групою, і$H \leq G\text{,}$ операція, індукована на$H$ косетах операцією,$G$ добре визначена.

Доказ

Припустимо, що$a\text{,}$$b\text{,}$ і$a'\text{,}$$b'\text{.}$ є два варіанти для представників косети$C$ і$D\text{.}$ Тобто, що$a, a' \in C\text{,}$$b, b' \in D\text{.}$ Ми покажемо, що$a*b$ і$a'*b'$ є представниками однієї і тієї ж косети. Теорема$\PageIndex{1}$ має на увазі, що$C = a*H$$a' \in a*H$ і$D = b*H\text{,}$ таким чином ми маємо і$b' \in b*H\text{.}$ тоді існує$h_1, h_2 \in H$ таке, що$a' = a*h_1$$b' = b*h_2$ і так

\ begin {рівняння*} a'*b' = (a*h_1) * (b*h_2) = (a*b) * (h_1*h_2)\ end {рівняння*}

за різними властивостями групи і припущенням, що$G$ є абелевим, що дозволяє нам змінити порядок, в якому$b$ і$h_1$ з'являються в ланцюжку рівностей. Цей останній вираз для$a'*b'$ означає, що$a'*b' \in (a*b)*H$$h_1*h_2 \in H$ оскільки оскільки$H$ є підгрупою$G\text{.}$ Таким чином, ми отримуємо однакову косету для обох пар представників.

Теорема$\PageIndex{5}$

Дозволяти$G$ бути групою і$H \leq G\text{.}$ Якщо операція індукована на лівих$H$ косетах операцією$G$ добре визначена, то набір лівих косетів утворює групу під цією операцією.

Доказ

Нехай$C_1$$,C_2\text{,}$ і$C_3$ будуть ліві косети з представниками$r_1\text{,}$$r_2\text{,}$ і$r_3\text{,}$ відповідно. Значення$C_1 \otimes \left(C_2 \otimes C_3\right)$ і$\left(C_1\ \otimes C_2\right)\otimes C_3$ визначаються$r_1 * \left(r_2 * r_3\right)$$\left(r_1 * r_2\right) * r_3\text{,}$ відповідно. За асоціативністю$*$ в$G\text{,}$ цих двох групах елементи рівні і тому два косетних вирази повинні бути рівними. Тому індукована операція носить асоціативний характер. Що стосується ідентичності та зворотних властивостей, то тут нікого не здивуєш. Ідентифікаційна косет - це$H\text{,}$ або$e*H\text{,}$ косет, який містить$G$ ідентичність. Якщо$C$ це косет з представником,$a\text{;}$ тобто, якщо$C = a*H\text{,}$ тоді$C^{-1}$ є$a^{-1}*H\text{.}$

\ begin {рівняння*} (A*h)\ раз\ ліворуч (a^ {-1} *H\ праворуч) =\ ліворуч (a*a^ {-1}\ праворуч) * H =\ textrm {ідентичність}\ textrm {coset}\ text {.} \ end {рівняння*}

Визначення $\PageIndex{4}$: Factor Group

$G$Дозволяти група і$H \leq G\text{.}$ Якщо множина лівих косет$H$ утворює групу, то ця група називається множником групи «по$G$ модулю$H\text{.}$» Він позначається$G/H\text{.}$

Примітка$\PageIndex{2}$

Якщо$G$ абелева, то кожна підгрупа$G$ дає групу факторів. Ми відкладемо подальший розгляд неабелевої справи до розділу 15.4.

Зауваження$\PageIndex{2}$: On Notation

Для роботи прийнято використовувати той самий символ, що і для операції. Причина, яку ми використовували різні символи в цьому розділі, полягала в тому, щоб чітко розмежувати дві операції.$G/H$$G\text{.}$

Вправи

Вправа$\PageIndex{1}$

Розглянемо$\mathbb{Z}_{10}$ і підмножини$\mathbb{Z}_{10}\text{,}$$\{0, 1, 2, 3, 4\}$ і$\{5, 6, 7, 8, 9\}\text{.}$ Чому операція індукована на ці підмножини за модулем 10 додавання недостатньо чітко визначена?

Відповідь: Приклад коректної відповіді: Викликати підмножини$A$ і$B$ відповідно. Якщо ми$5 \in B$ вибираємо$0 \in A$ і$0 +_{10} 5 =5 \in B\text{.}$ отримуємо З іншого боку, якщо ми вибираємо$3 \in A$ і$8 \in B\text{,}$ отримуємо$3 +_{10} 8 = 1 \in A\text{.}$ Отже, індукована операція не визначена на$\{A,B\}\text{.}$

Вправа$\PageIndex{2}$

Чи можете ви придумати групу$G\text{,}$ з$H$ такою підгрупою, що$\lvert H\rvert = 6$ і$\lvert G/H\rvert = 6\text{?}$ Ваша відповідь унікальна?

Вправа$\PageIndex{3}$

Для кожної групи та підгрупи, що є$G/H$ ізоморфним?

$G = \mathbb{Z}_4 \times \mathbb{Z}_2$і$H = \langle (2, 0)\rangle\text{.}$ Порівняти з прикладом$\PageIndex{5}$.
$G = [\mathbb{C}; +]$і$H = \mathbb{R}\text{.}$
$G$=$\mathbb{Z}_{20}$ і$H = \langle 8\rangle\text{.}$

Відповідь

Чотири різні косети в$G/H$ є$H = \{(0, 0), (2, 0)\}\text{,}$$(1, 0) + H= \{(1,0),(3,0)\}\text{,}$$(0, 1) + H= \{(0,1),(2,1)\}\text{,}$ і$(1, 1) + H= \{(1,1),(3,1)\}\text{.}$ Жодна з цих косетів генерує,$G/H\text{;}$ отже, не$G/H$ є циклічною. Отже,$G/H$ повинен бути ізоморфним до$\mathbb{Z}_2\times \mathbb{Z}_2\text{.}$
Група факторів ізоморфна до$[\mathbb{R}; +]\text{.}$ Кожній косети$\mathbb{R}$ є лінією в комплексній площині, яка паралельна осі х:$\tau :\mathbb{C}/\mathbb{R}\to \mathbb{R}\text{,}$ де$T(\{a + b i\mid a\in \mathbb{R}\}) = b$ - ізоморфізм.
$\langle 8\rangle = \{0, 4, 8, 12, 16\} $$\Rightarrow$$\lvert \mathbb{Z}_{20}/\langle 8\rangle \rvert =4\text{.}$Чотири косети:$\bar{0}\text{,}$$\bar{1}\text{,}$$\bar{2}\text{,}$ і$\bar{3}\text{.}$ 1 генерує всі чотири косети. Група факторів ізоморфна,$[\mathbb{Z}_4; +_4]$ тому що$\bar{1}$ є генератором.

Вправа$\PageIndex{4}$

Для кожної групи та підгрупи, що є$G/H$ ізоморфним?

$G = \mathbb{Z}\times \mathbb{Z}$і$H = \{(a, a) | a \in \mathbb{Z}\}\text{.}$
$G = \left[\mathbb{R}^*; \cdot \right]$і$H = \{1, -1\}\text{.}$
$G =\mathbb{Z}_2{}^5$і$H = \langle (1, 1, 1, 1, 1)\rangle\text{.}$

Вправа$\PageIndex{5}$

Припустімо, що$G$ це група,$H \leq G\text{,}$ і$a, b \in G\text{.}$ довести, що$a*H= b*H$ якщо і тільки якщо$b^{-1}*a \in H\text{.}$

Відповідь: \ begin {рівняння*}\ почати {спліт} A*h = B*h &\ Стрілка вліворуч a\ in b H\\ &\ Стрілка вліворуч a = b * h\ textrm {для деяких} h\ in H\\ &\ Стрілка вліворуч b ^ {-1} *a = h\ textrm {для деяких} h\ в H\\ &\ Ліворуч Стрілка b^ {-1} *a\ in H\\ end {split}\ end {рівняння*}

Вправа$\PageIndex{6}$

Реальне додавання по модулю$r\text{,}$$r > 0\text{,}$ можна описати як операцію, індуковану на косетах звичайного додавання.$\langle r\rangle$ Охарактеризуйте систему видатних представників для елементів$\mathbb{R}/\langle r\rangle\text{.}$
Розглянемо тригонометричну функцію синус. З огляду$\sin (x+2\pi k) = \sin x$ на, що для всіх$x\in \mathbb{R}$ і$k\in \mathbb{Z}\text{,}$ показати, наскільки виділяються представники$\mathbb{R}/\langle 2\pi \rangle$ можуть стати в нагоді при розробці алгоритму обчислення синуса того чи іншого числа.

Вправа$\PageIndex{7}$

Завершіть доказ теореми,$\PageIndex{2}$ доводячи, що якщо$a \in G\text{,}$$\rho:H \to a*H$ визначено$\rho(h)= a*h$, це біекція.