15.1: Циклічні групи

Last updated
Save as PDF

Page ID: 65080

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Групи класифікуються за розмірами і структурою. Структура групи виявляється шляхом вивчення її підгруп та інших властивостей (наприклад, чи є вона абелевою), які можуть дати її огляд. Циклічні групи мають найпростішу будову з усіх груп.

Визначення$\PageIndex{1}$: Cyclic Group

Група$G$ є циклічною, якщо існує$a \in G$ така, що циклічна підгрупа генерується$a\text{,}$$\langle a \rangle\text{,}$ рівною всім That is,$G = \{n a |n \in \mathbb{Z}\}\text{,}$ в цьому випадку$a$ називається генератором. Читач повинен$G\text{.}$ зауважити, що адитивні позначення використовуються для$G\text{.}$$G\text{.}$

Приклад$\PageIndex{1}$: A Finite Cyclic Group

$\mathbb{Z}_{12} = [\mathbb{Z}_{12}; +_{12} ]\text{,}$де$+_{12}$ додається по модулю 12, являє собою циклічну групу. Щоб перевірити це твердження, все, що нам потрібно зробити, це продемонструвати, що якийсь елемент$\mathbb{Z}_{12}$ є генератором. Одним з таких елементів є 5; тобто ще$\langle 5 \rangle = \mathbb{Z}_{12}\text{.}$ одним очевидним генератором є 1. Насправді, 1 є генератором кожного читача$[\mathbb{Z}_n; +_n]\text{.}$ просять довести, що якщо елемент є генератором, то його зворотний також є генератором. Таким чином,$-5 = 7$ і$-1 = 11$ є іншими генераторами$\mathbb{Z}_{12}\text{.}$ Решта вісім елементів групи не є генераторами.

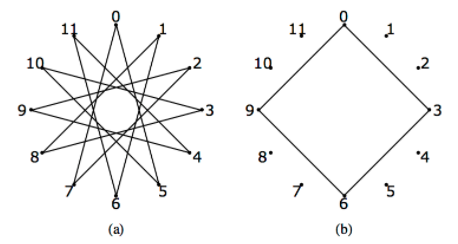$clipboard_e9f92697da347bcde751b04e8fecf8bb5.png$ Малюнок $\PageIndex{1}$: Скопіюйте та вставте підпис тут. (Авторське право; автор через джерело)

Рисунок$\PageIndex{1}$ (а) є прикладом «струнного мистецтва», який ілюструє, як 5 генерує$\mathbb{Z}_{12}\text{.}$ Дванадцять прихваток розміщуються рівномірно навколо кола і нумеруються від 0 до 11. Рядок прив'язується до прихватки 0, а потім петельно навколо кожної п'ятої прихватки. В результаті числа досягнутих тактів є точно впорядкованими кратними 5 по модулю 12:5, 10, 3,..., 7, 0. Зауважте, що якби використовувалася кожна сьома прихватка, буде створено однакові ілюстрації. Якби кожна третя прихватка була з'єднана, як на малюнку$\PageIndex{1}$ (b), отримана петля використовувала б лише чотири прихватки; таким чином 3 не генерує$\mathbb{Z}_{12}\text{.}$

Приклад$\PageIndex{2}$: The Group of Integers is Cyclic

Адитивна група цілих чисел,$[\mathbb{Z}; +]\text{,}$ циклічна:

\ begin {рівняння*}\ mathbb {Z} =\ кут 1\ діапазон =\ {n\ cdot 1 |n\ in\ mathbb {Z}\}\ кінець {рівняння*}

Це спостереження не означає, що кожне ціле число є добутком цілого числа на 1. Це означає, що

\ почати {рівняння*}\ mathbb {Z} =\ {0\}\ чашка\ {\ накладення {1+1+\ cdots +1} ^ {n\ textrm {terms}}\ mathbb {P}\ чашка\ {\ накладення {(-1) +\ cdots + (-1) +\ cdots + (-1)} ^ {n\ текст m {terms}}\ середина n\ in\ mathbb {P}\}\ end {рівняння*}

Теорема$\PageIndex{1}$: Cyclic Implies Abelian

Якщо$[G;*]$ циклічний, то він абелевий.

Доказ

$a$Дозволяти будь генератор$G$ і нехай$b, c \in G\text{.}$ За визначенням генератора групи існують цілі числа$m$ і$n$ такі, що$b = m a$ і$c = n a\text{.}$ Таким чином, використовуючи теорему 11.3.9,

\ begin {рівняння*}\ почати {спліт} b* c &= (м а) * (n a)\\ &= (м + n) a\\ &= (n + m) a\\ &= (n a) * (m a)\ &= c*b\\\ end {спліт}\ кінець {рівняння*}

Одним з перших кроків у доведенні властивості циклічних груп є використання того факту, що існує генератор. Тоді кожен елемент групи може бути виражений у вигляді деякого кратного генератору. Зверніть особливу увагу на те, як це використовується в теоремах цього розділу.

До теперішнього часу ми використовували лише адитивні позначення для обговорення циклічних груп. Теорема$\PageIndex{1}$ фактично виправдовує цю практику, оскільки при обговоренні абелевих груп прийнято використовувати адитивні позначення. Звичайно, деякі конкретні групи, для яких ми використовуємо мультиплікативні позначення, є циклічними. Якщо один з його елементів,$a\text{,}$ є генератором,

\ begin {рівняння*}\ кут a\ діапазон =\ лівий\ {a^n\ mid n\ in\ mathbb {Z}\ право\}\ end {рівняння*}

Приклад$\PageIndex{3}$: A Cyclic Multiplicative Group

Група натуральних чисел по модулю 11 з множенням по модулю 11,$[\mathbb{Z}_{11}^* ;\times_{11}]\text{,}$ є циклічною. Одним з його генераторів є 6:$6^1 = 6\text{,}$$6^2 = 3\text{,}$$6^3= 7\text{,}$$\ldots$,$6^9=2\text{,}$ і$6^{10}=1\text{,}$ ідентичність групи.

Приклад$\PageIndex{4}$: A Non-Cyclic Group

Дійсні числа з додаванням,$[\mathbb{R};+]$ є нециклічною групою. Доказ цього твердження вимагає трохи більшої загальності, оскільки ми говоримо, що для всіх$r \in \mathbb{R}\text{,}$$\langle r \rangle$ є належною підмножиною$\mathbb{R}\text{.}$ Якщо$r$ ненульова, кратні$r$ розподіляються по дійсній лінії, як на малюнку$\PageIndex{2}$. Зрозуміло тоді, що існує багато дійсних чисел$r/2\text{,}$, таких як не в$\langle r \rangle\text{.}$

$clipboard_e8cc675a8ee91924fa0ab8ec3bc0145ae.png$ Малюнок$\PageIndex{2}$: Елементи$\langle r \rangle, r>0$

Наступні два докази використовують теорему 11.4.1.

Наступна теорема показує, що циклічна група ніколи не може бути дуже складною.

Теорема$\PageIndex{2}$: Possible Cyclic Group Structures

Якщо$G$ це циклічна група, то$G$ вона або скінченна, або зліченно нескінченна. Якщо$G$ скінченний і$\lvert G\rvert=n\text{,}$ ізоморфний до$[\mathbb{Z}_n; +_n]\text{.}$ If$G$ нескінченний, він ізоморфний до$[\mathbb{Z};+]\text{.}$

Доказ

Випадок 1:$\lvert G\rvert < \infty\text{.}$ Якщо$a$ є генератором$G$ і$\lvert G\rvert =n\text{,}$$\phi:\mathbb{Z}_n \to G$ визначено$\phi(k) = k a$ для всіх$k \in \mathbb{Z}_n\text{.}$

Оскільки$\langle a \rangle$ є кінцевим, ми можемо використовувати той факт, що елементи$\langle a \rangle$ є першими$n$ невід'ємними кратними$a\text{.}$ з цього спостереження, ми бачимо, що$\phi$ це сюрекція. Сюркція між скінченними множинами однакової кардинальності повинна бути біекцією. Нарешті, якщо$p,q \in \mathbb{Z}_n\text{,}$

\ begin {рівняння*}\ почати {спліт}\ phi (p) +\ phi (q) &= p a + q a\\ &= (p+q) a\\ &= (p +_n q) a\ quad\ textrm {див. вправу 15.1.10}\\ & =\ phi (p +_n q)\\ кінець {спліт}\ кінець {рівняння*}

Тому$\phi$ є ізоморфізм.

Випадок 2:$\lvert G\rvert =\infty\text{.}$ Ми залишимо цю справу як вправу.

Теорема$\PageIndex{3}$: Subgroups of Cyclic Groups

Кожна підгрупа циклічної групи є циклічною.

Доказ: $G$Дозволяти циклічний з генератором$a$ і$H \leq G\text{.}$ нехай$H = \{e\}\text{,}$$H$$e$ If має як генератор. Тепер ми можемо припустити, що$\lvert H\rvert \geq 2$ і$a \neq e\text{.}$$m$ Дозволяти бути найменш позитивним цілим таким, що$m a$ належить$H\text{.}$ Це ключовий крок. Це дозволяє нам отримати наші руки на генератор$H\text{.}$ Ми тепер покажемо, що$c= m a$ породжує$H\text{.}$ Звичайно,$\langle c \rangle \subseteq H\text{,}$ але припустимо, що$\langle c \rangle \neq H\text{.}$ Тоді існує$b \in H$ таке, що$b \notin \langle c \rangle\text{.}$ Зараз, оскільки$b$ є$G\text{,}$ там існує$n \in \mathbb{Z}$ таке, що$b = n a\text{.}$ Тепер ми застосовуємо властивість поділу і ділимо$n$ на$m\text{.}$$b = n a = (q m+r)a = (q m)a+r a\text{,}$ де$0 \leq r < m\text{.}$ ми зауважимо, що$r$ не може бути нулем, бо інакше ми б мали$b = n a = q(m a) = q c \in \langle c \rangle\text{.}$ Тому,$r a = n a - (q m) a \in H\text{.}$ Це суперечить нашому вибору,$m$ тому що$0 < r < m\text{.}$

Приклад$\PageIndex{5}$: All Subgroups of $\mathbb{Z}_{10}$

Єдиними власними підгрупами$\mathbb{Z}_{10}$ є$H_1 = \{0, 5\}$ і$H_2 = \{0, 2, 4, 6, 8\}\text{.}$ Вони обидва циклічні:$H_2 = \langle 2 \rangle = \langle 4 \rangle = \langle 6 \rangle = \langle 8 \rangle\text{.}$ в$H_1= \langle 5 \rangle\text{,}$ той час як$\mathbb{Z}_{10}$ генератори 1, 3, 7 і 9.

Приклад$\PageIndex{6}$: All Subgroups of $\mathbb{Z}$

За винятком$\{0\}\text{,}$ усіх підгруп$\mathbb{Z}$ ізоморфних до$\mathbb{Z}\text{.}$ If,$H \leq \mathbb{Z}\text{,}$ то$H$ циклічна підгрупа, породжена найменш позитивним елементом It нескінченна, і тому за теоремою$\PageIndex{3}$ вона ізоморфна$H\text{.}$$\mathbb{Z}\text{.}$

Наведемо корисну теорему для обчислення порядку циклічних підгруп циклічної групи:

Теорема$\PageIndex{4}$: The Order of Elements of a Finite Cyclic Group

Якщо$G$ є циклічною групою порядку$n$ і$a$ є$G\text{,}$ генератором порядку$k a$$d$ є$n/d\text{,}$ де найбільший спільний дільник$n$ і$k\text{.}$

Доказ: Доказ цієї теореми залишається читачеві.

Приклад$\PageIndex{7}$: Computation of an Order in a Cyclic Group

Для обчислення порядку$\langle 18 \rangle$ в$\mathbb{Z}_{30}\text{,}$ ми спочатку спостерігаємо, що 1 є генератором$\mathbb{Z}_{30}$ і$18= 18(1)\text{.}$ Найбільшим спільним дільником 18 і 30 є 6. Значить, порядок$\langle 18 \rangle$ становить 30/6, або 5.

На цьому етапі ми представимо ідею швидкого суматора, відносно сучасного застосування (Winograd, 1965) давньої теореми, китайської теореми про залишок. Ми представимо лише огляд теорії і спираємося насамперед на приклади.

З необхідності додавання цілих чисел за допомогою комп'ютера є додавання по модулю$n\text{,}$ для$n$ деякого більшого числа. Розглянемо випадок,$n$ коли маленький, як 64. Тоді додавання передбачає складання шестизначних двійкових чисел. Розглянемо процес додавання 31 і 1. Припустимо, що суматор комп'ютера приймає як вхідні два бітові рядки$a = \left\{a_0,a_1,a_2,a_3,a_4,a_5\right\}$$b=\left\{b_0,b_1,b_2,b_3,b_4,b_5\right\}$$a$ і виводить$s = \left\{s_0,s_1,s_2,s_3,s_4,s_5\right\}\text{,}$ суму$a = 31 = (1, 1, 1, 1, 1, 0)$ і$b\text{.}$ тоді, якщо і$b = 1 = (1, 0, 0, 0, 0, 0)\text{,}$$s$ буде (0, 0, 0, 0, 0, 1), або 32. Вихід$s_{ }=1$ не може бути визначено, поки не будуть визначені всі інші виходи. Якщо додавання виконується за допомогою кінцевої машини, як у прикладі 14.3.5, час, необхідний для отримання,$s$ складе шість одиниць часу, де одна одиниця часу - це час, необхідний для отримання одного виходу з машини. В цілому час, необхідний для отримання,$s$ буде пропорційно кількості бітів. Теоретично цей час можна зменшити, але пояснення вимагало б тривалого відступу, і наші відносні результати не зміниться так сильно. Ми будемо використовувати правило, що кількість одиниць часу, необхідних для виконання складання по модулю$n$, пропорційна$\left\lceil \log_2n\right\rceil\text{.}$

Тепер ми представимо гіпотетичну проблему, яку будемо використовувати для ілюстрації ідеї швидкого суматора. Припустимо, що нам довелося додати 1000 чисел$27720 = 8 \cdot 9 \cdot 5 \cdot 7\cdot 11\text{.}$ по модулю за правилом вище, так як$2^{14} < 27720 < 2^{15}\text{,}$ кожне додавання займе 15 одиниць часу. Якщо сума ініціалізується нулем, знадобиться 1000 доповнень; таким чином, 15 000 одиниць часу знадобиться для виконання доповнень. Ми можемо значно покращити цей час, застосувавши китайську теорему про залишок.

Теорема$\PageIndex{5}$: Chinese Remainder Theorem (CRT)

$n_1\text{,}$$n_2\text{,}$$\ldots\text{,}$$n_p$Дозволяти цілі числа, які не мають спільного коефіцієнта більше одиниці між будь-якою парою з них; тобто, вони є відносно простими. Дозвольте$n = n_1n_2\cdots n_p\text{.}$ визначити

\ begin {рівняння*}\ thet a:\mathbb {Z} _n\ до\ mathbb {Z} _ {n_1}\ раз\ mathbb {Z} _ {n_2}\ час\ cdots\ час\ mathbb {Z} _ {n_p}\ кінець {рівняння*}

від

\ begin {рівняння*}\ тета (k) =\ лівий (k_1, k_2,\ ldots, k_p\ правий)\ end {рівняння*}

де для$1\leq i\leq p\text{,}$$0\leq k_i < n_i$ і$k\equiv k_i\left(\textrm{mod } n_i\right)\text{.}$ Тоді$\theta$ - ізоморфізм з$\mathbb{Z}_n$ в$\mathbb{Z}_{n_1}\times \mathbb{Z}_{n_2}\times \cdots \times \mathbb{Z}_{n_p}\text{.}$

Китайська теорема про залишок може бути викладена в декількох різних формах, і її доказ можна знайти в багатьох текстах абстрактної алгебри.

Як ми бачили в главі 11,$\mathbb{Z}_6$ є ізоморфним до$\mathbb{Z}_2 \times \mathbb{Z}_3$. Це найменший випадок, до якого може застосовуватися ЕПТ. Ізоморфізм між$\mathbb{Z}_6$ і$\mathbb{Z}_2 \times \mathbb{Z}_3$ є

\ begin {рівняння*}\ почати {масив} {cc}\ тета (0) = (0,0) &\ тета (3) = (1,0)\\ тета (1) = (1, 1) &\ тета (4) = (0, 1)\\ тета (2) = (0, 2) &\ тета (5) = (1,2)\\ кінець {масив} {рівняння*}

Розглянемо дещо більший випадок. Ми почнемо з вибору модуля, який може бути врахований у добуток відносно простих цілих чисел:$n=21,600=2^5 3^3 5^2\text{.}$ У цьому випадку множники є$2^5=32\text{,}$$3^3=27\text{,}$ і$5^2=25\text{.}$ Вони не повинні бути степенями простих чисел, але легко розбити множники на цю форму, щоб забезпечити відносно прості числа. Для додавання$\mathbb{Z}_n\text{,}$ нам потрібні одиниці$\left\lceil \log _2n\right\rceil =15$ часу. Нехай$G=\mathbb{Z}_{32}\times \mathbb{Z}_{27}\times \mathbb{Z}_{25}\text{.}$ ЕПТ дає нам ізоморфізм між$\mathbb{Z}_{21600}$ і$G\text{.}$ Основна ідея швидкого суматора, проілюстрована на малюнку$\PageIndex{3}$, полягає в тому, щоб використовувати цей ізоморфізм. Позначення x += a інтерпретується як інструкція додати значення a до змінної x.

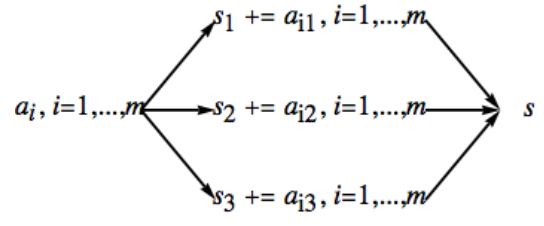$clipboard_e1ed5154c9c034939fac27b264b70829c.png$ Малюнок$\PageIndex{3}$: Швидка схема суматора

Припустимо, у нас є кілька цілих$a_1, \ldots , a_m$ чисел, які потрібно додати. Тут ми припускаємо, що$m= 20\text{.}$ ми обчислюємо суму s, щоб порівняти наш результат з цією істинною сумою.

a=[1878,1384,84,2021,784,1509,1740,1201,2363,1774,
   1865,33,1477,894,690,520,198,1349,1278,650]
s =0
for t in a:
    s+=t
s

Хоча наша сума є цілим обчисленням, ми поставимо наше обчислення в контексті цілих чисел по модулю 21600. Ізомофізм від$\mathbb{Z}_{21600}$ в Sage$G=\mathbb{Z}_{32}\times \mathbb{Z}_{27}\times \mathbb{Z}_{25}$ визначається як тета. Крім того, ми демонструємо, що операції в цих групах зберігаються за допомогою тета.

G=cartesian_product([Integers(32),Integers(27),Integers(25)])
def theta(x):
    return G((x%32,x%27,x%25))
[theta(1878)+theta(1384),theta(1878+1384)]

Ми ініціалізуємо суми в кожному множнику діапазону тета до нуля і розкладаємо кожну суму$t$ на трійку$\theta(t)=\left(t_1,t_2,t_3\right)\in G\text{.}$

sum=G((0,0,0))
for t in a:
    sum+=theta(t)
sum

Додавання в$G$ може бути зроблено паралельно так, що кожен новий проміжний підсумок у вигляді трійки$(s_1,s_2, s_3)$ займає лише стільки часу, щоб обчислити, скільки потрібно, щоб додати найбільший модуль, одиниці$\log _232=5$ часу, якщо обчислення проводяться паралельно. За правилом часу, яке ми встановили, додавання чисел 20 можна зробити в одиницях$20\cdot 5= 100$ часу, на відміну від одиниць$20\cdot 15 =300$ часу, якщо ми робимо обчислення в$\mathbb{Z}_{21600}\text{.}$ Однак результат є потрійним у$G\text{.}$ Функція, яка виконує зворотну тета вбудована в більшість математичні програми, в тому числі Sage. У Sage функція crt. Ми використовуємо цю функцію для обчислення зворотного нашого потрійного, який є елементом$\mathbb{Z}_{21600}\text{.}$ Результат не є істинною сумою, оскільки модуль 21600 недостатньо великий. Однак ми перевіряємо, що наш результат збігається з істинною сумою за модулем 21600.

isum=crt([12,13,17],[32,27,25])
[isum,(s-isum)%(21600)]

Для того щоб отримати справжню суму з нашої схеми, модуль потрібно було б збільшити, перейшовши від 21600 до, наприклад,$21600*23=496800\text{.}$ Відображення в нову групу,$G=\mathbb{Z}_{32}\times \mathbb{Z}_{27}\times \mathbb{Z}_{25}\times \mathbb{Z}_{23}$ займе трохи більше часу, як і процес інверсії з crt, але додавання доданих, які знаходяться у вигляді чотирикраток можна зробити без додаткового часу.

Обчислення$\theta^{-1}\left(s_1,s_2,s_3\right)$ цього здійснюється за допомогою функції Sage crt може бути здійснено різними способами. Всі вони в кінцевому підсумку спрощуються тим, що також$\theta^{-1}$ є ізоморфізмом. Один з підходів полягає у використанні властивості ізоморфізму, щоб зрозуміти, що значення$\theta^{-1}\left(s_1,s_2,s_3\right)$ є$s_1\theta^{-1}(1,0,0)+s_2\theta^{-1}(0,1,0)+s_3\theta^{-1}(0,0,1)\text{.}$ Арифметика в цьому виразі знаходиться в області$\theta$ і є більш трудомістким, але це потрібно зробити лише один раз. Ось чому швидкий суматор практичний лише в тих ситуаціях, коли необхідно виконати багато доповнень, щоб отримати єдину суму.

Обернені зображення «одиничних векторів» можна обчислити достроково.

u=[crt([1,0,0],[32,27,25]),
   crt([0,1,0],[32,27,25]),crt([0,0,1],[32,27,25])]
u

Результат, який ми обчислили раніше, можна обчислити безпосередньо в більшому модулі.

(7425*12 + 6400*13+ 7776* 17)%21600

Щоб додатково проілюструвати потенціал швидких суматорів, розгляньте можливість збільшення модуля до$n=2^53^35^27^211\cdot 13\cdot 17\cdot 19\cdot 23\cdot 29\cdot 31\cdot 37\cdot 41\cdot 43\cdot 47\approx 3.1\times 10^{21}\text{.}$ Кожне додавання за допомогою звичайного$n$ додавання по модулю з повними суматорами займе 72 одиниці часу. Розкладаючи кожен сумунт на 15-кортежі відповідно до ЕПТ, час скорочується до одиниць$\left\lceil \log _249\right\rceil =6$ часу на додавання.

Вправи

Вправа$\PageIndex{1}$

Які генератори крім 1$[\mathbb{Z}; +]$ мають?

Відповідь: Єдиним іншим генератором є$-1\text{.}$

Вправа$\PageIndex{2}$

Припустимо,$[G;*]$ це циклічна група з генератором$g\text{.}$ Якщо ви будуєте граф з вершинами з елементів$G$ та набору ребер, як$E= \{(a, g*a) \mid a\in G\}\text{,}$ виглядатиме графік? Якщо$G$ група парного порядку, як$E'= \{(a, g^2*a) \mid a\in G\}$ виглядатиме графік із набором країв?

Вправа$\PageIndex{3}$

Доведіть, що якщо$\lvert G \rvert >2$ і$G$ циклічний,$G$ має принаймні два генератори.

Відповідь

Якщо$\lvert G \rvert = m\text{,}$$m>2\text{,}$ і$G = \langle a \rangle\text{,}$ тоді$a\text{,}$$a^2,\ldots\text{,}$$a^{m-1}$,$a^m=e$ є окремими елементами$G\text{.}$ Крім того,$a^{-1}= a^{m-1}\neq a\text{,}$ Якщо$1 \leq k \leq m\text{,}$$a^{-1}$ генерує$a^k\text{:}$

\ begin {рівняння*}\ почати {спліт}\ ліворуч (a^ {-1}\ праворуч) ^ {м-k} &=\ ліворуч (a^ {м-1}\ праворуч) ^ {м-k}\\ & = a^ {m^2-м-м k + k}\\ & =\ ліворуч (a^m\ праворуч) ^ {м-k-1} *a^k\\ = e*^a* k=a^k\\ кінець {спліт}\ кінець {рівняння*}

Аналогічно, якщо$G$ нескінченно, а$G = \langle a\rangle\text{,}$ потім$a^{-1}$ генерує$G\text{.}$

Вправа$\PageIndex{4}$

Якщо ви хочете перерахувати генератори,$\mathbb{Z}_n$ вам доведеться лише перевірити перші$n/2$ натуральні числа. Чому?

Вправа$\PageIndex{5}$

Які з перерахованих нижче груп є циклічними? Поясніть.

$\displaystyle [\mathbb{Q}; +]$
$\displaystyle [\mathbb{R}^+;\cdot ]$
$[6\mathbb{Z}; +]$де$6\mathbb{Z} = \{6n |n \in \mathbb{Z}\}$
$\displaystyle \mathbb{Z} \times \mathbb{Z}$
$\displaystyle \mathbb{Z}_2\times \mathbb{Z}_3 \times \mathbb{Z}_{25}$

Відповідь

Ні. Припустимо, що$q \in \mathbb{Q}$ генерує$\mathbb{Q}\text{.}$ Тоді$\langle q\rangle = \{n q : n \in \mathbb{Z}\}\text{.}$ Але це дає нам не більше цілих кратних$q\text{,}$ не кожен елемент в$\mathbb{Q}\text{.}$
Ні. Подібні міркування до частини а.
Так. 6 - це генератор$6\mathbb{Z}\text{.}$
Ні.
Так,$(1,1, 1)$ є генератором групи.

Вправа$\PageIndex{6}$

Для кожної групи і елемента визначте порядок циклічної підгрупи, що генерується елементом:

$\mathbb{Z}_{25}$, 15
$\mathbb{Z}_4\times \mathbb{Z}_9$,$(2, 6)$ (застосувати вправу$\PageIndex{8}$)
$\mathbb{Z}_{64}$, 2

Вправа$\PageIndex{7}$

Як теорема може$\PageIndex{4}$ бути застосована до переліку генераторів$\mathbb{Z}_n\text{?}$ Що таке генератори$\mathbb{Z}_{25}\text{?}$ Of$\mathbb{Z}_{256}\text{?}$

Відповідь: Теорема$\PageIndex{4}$ передбачає, що$a$ генерує$\mathbb{Z}_n$ тоді і тільки тоді, коли найбільший спільний дільник$n$ і$a$ дорівнює 1. Тому список генераторів$\mathbb{Z}_n$ є цілими числами$\mathbb{Z}_n$, які є відносно$n\text{.}$ простими до генераторів$\mathbb{Z}_{25}$ всіх ненульових елементів, крім 5, 10, 15 та 20. Генератори$\mathbb{Z}_{256}$ є непарними цілими числами в$\mathbb{Z}_{256}$ починаючи з 256$2^8\text{.}$

Вправа$\PageIndex{8}$

Доведіть, що якщо найбільший спільний дільник$n$ і$m$ є 1, то (1, 1) є генератором$\mathbb{Z}_n\times \mathbb{Z}_m\text{,}$ і, отже,$\mathbb{Z}_n\times \mathbb{Z}_m$ ізоморфний до$\mathbb{Z}_{n m}\text{.}$

Вправа$\PageIndex{9}$

Проілюструйте, як швидкий суматор може бути використаний для додавання чисел 21, 5, 7 і 15, використовуючи ізоморфізм між$\mathbb{Z}_{77}$ і$\mathbb{Z}_7\times \mathbb{Z}_{11}\text{.}$
Якщо ж ізоморфізм використовується для додавання чисел 25, 26 і 40, яким буде результат, чому б він був неправильним, і чим би відповідь відрізнялася від відповіді в частині a?

Відповідь

$\theta :\mathbb{Z}_{77} \to \mathbb{Z}_7 \times \mathbb{Z}_{11}$відображає задані цілі числа наступним чином:
\ begin {рівняння*}\ begin {масив} {ccc} 21 &\ до & (0,10)\\ 5 &\ to & (5,5)\\ 7 &\ to & (0,7)\\ 15 &\ до &\\ підкреслення {(1,4)}\\ textrm {сума} =48 &\ leftarrow & (6,4)\\ = текст {сума}\\ кінець {масив}\ кінець { рівняння*}
Остаточна сума, 48, отримана за допомогою фактів, що$\theta ^{-1}(1,0) =22$ і$\theta ^{-1}(0,1)=56$
\ починаються {рівняння*}\ починаються {спліт}\ тета^ {-1} (6,4) = 6\ times_ {77}\ theta ^ {-1} (1,0) + 4\ times_ {77}\ theta^ {-1} (0,1)\\ & =6\ times_ {77} +_ {77}} 4\ часі_ {77} 56\\ & =55 +_ {77} 70\\ & =48\\\ кінець {спліт}\ текст {.} \ end {рівняння*}
Використання того ж ізоморфізму:
\ begin {рівняння*}\ begin {масив} {ccc} 25 &\ to & (4,3)\\ 26 &\ to & (5,4)\\ 40 &\ to & (5,7)\\ & &\ textrm {сума} =( 0,3)\\ кінець {масив}\ кінець {рівняння*}
\ begin {рівняння*}\ begin {спліт}\ тета ^ {-1} (0,3) &= 3\ times_ {77}\ тета ^ {-1} (0,1)\\ & = 3\ times_ {77} 56\\ & =14\\ кінець {спліт}\ текст {.} \ end {рівняння*}
Фактична сума дорівнює 91. Наш результат невірний, оскільки 91 не в$\mathbb{Z}_{77}\text{.}$ Примітці, що 91 і 14 відрізняються на 77. Будь-яка помилка, яку ми отримуємо, використовуючи цю техніку, буде кратна 77.

Вправа$\PageIndex{10}$

Доведіть,$G$ що якщо циклічна група порядку$n$ з генератором,$a\text{,}$ а$p, q \in \{0, 1, \ldots , n - 1\}\text{,}$ потім$(p+q)a = \left(p+_nq\right)a\text{.}$