12.4: Похідні
- Page ID
- 61371
Середній підліток у Сполучених Штатах відкриває двері холодильника приблизно 25 разів на день. Імовірно, цей середній показник перевищує 10 років тому, коли середній підліток відкривав двері холодильника 20 разів на день 1. За оцінками, телевізор увімкнено вдома 6.75 годин на день, тоді як батьки витрачають приблизно 5, 5 хвилин на день, маючи змістовну розмову зі своїми дітьми. Ці середні показники теж не такі, як вони були 10 років тому, коли телебачення було на приблизно 6 годин на день у типовому домогосподарстві, а батьки витрачали 12 хвилин на день у змістовній розмові зі своїми дітьми. Що спільного у цих сценаріїв? Функції, що їх представляють, змінювалися з плином часу. У цьому розділі ми розглянемо методи обчислення таких змін з плином часу.
Пошук середньої швидкості зміни функції
Функції, що описують наведені вище приклади, передбачають зміну з часом. Зміна, поділена на час, є одним із прикладів ставки. Темпи змін у попередніх прикладах різні. Іншими словами, одні змінювалися швидше за інших. Якби ми графували функції, ми могли б порівняти швидкості, визначаючи нахили графіків.
Дотична лінія до кривої - це лінія, яка перетинає криву лише в одній точці, але не перетинає її там. (Дотична лінія може перетинати криву в іншій точці від точки інтересу.) Якщо ми збільшимо криву в цій точці, крива виглядає лінійною, а нахил кривої в цій точці близький до нахилу дотичної лінії в цій точці.
Малюнок\(\PageIndex{1}\) представляє функцію\(f(x)=x^3−4x\). Ми можемо бачити нахил в різних точках вздовж кривої.
- ухил при\(x=−2\) дорівнює 8
- ухил при\(x=−1\) дорівнює —1
- ухил при\(x=2\) дорівнює 8
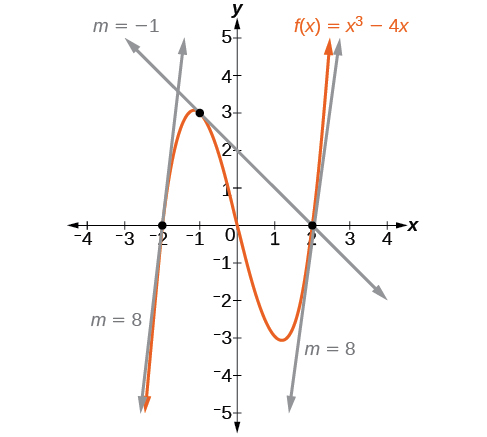
Уявімо точку на кривій функції в,\(x=a\) як показано\(f\) на малюнку\(\PageIndex{1}\). Координати точки є\((a,f(a))\). З'єднайте цю точку з другою точкою на кривій трохи праворуч від\(x=a\), зі значенням x, збільшеним на деяке невелике дійсне число\(h\). Координати цієї другої точки є\((a+h,f(a+h))\) для деякого позитивного значення\(h\).
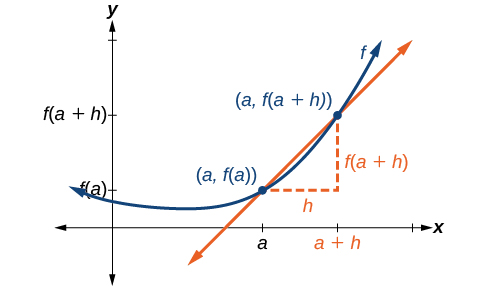
Ми можемо обчислити нахил лінії, що з'єднує дві точки\((a,f(a))\) і\((a+h,f(a+h))\), звану січною лінією, застосувавши формулу нахилу,
\[ \mathrm{slope = \dfrac{change \; in \; y}{change \; in \; x}} \]
Використовуємо позначення\(m_{sec}\) для представлення нахилу січної лінії, що з'єднує дві точки.
\[\begin{align} m_{sec} &= \dfrac{f(a+h)−f(a)}{(a+h)−(a) } \\ &= \dfrac{f(a+h)−f(a)}{\cancel{a}+h−\cancel{a}} \end{align}\]
Нахил\(m_{sec}\) дорівнює середній швидкості зміни між двома точками\((a,f(a))\) і\((a+h,f(a+h)).\)
\[m_{sec}=\dfrac{f(a+h)−f(a)}{h}\]
СЕРЕДНЯ ШВИДКІСТЬ ЗМІНИ МІЖ ДВОМА ТОЧКАМИ НА КРИВІЙ
Середня швидкість зміни (AROC) між двома точками\((a,f(a))\) і\((a+h,f(a+h))\) на кривій -\(f\) це нахил лінії, що з'єднує дві точки і задається
\[\text{AROC}=\dfrac{f(a+h)−f(a)}{h}\]
Приклад\(\PageIndex{1}\): Finding the Average Rate of Change
Знайти середню швидкість зміни, що з'єднують точки\((2,−6)\) і\((−1,5)\).
Рішення
Ми знаємо, що середня швидкість зміни, що з'єднує дві точки, може бути дана
\[\text{AROC}=\dfrac{f(a+h)−f(a)}{h}\]
Якщо одна точка є\((2,−6)\), або\((2,f(2))\), то\(f(2)=−6.\)
Значення\(h\) -\(2\) зсув від до\(−1\), яке дорівнює\(−1−2=−3.\)
Для іншої точки\(f(a+h)\) - це y -координата at\(a+h\), яка є\(2+(−3)\) або близько\(−1,\) того\(f(a+h)=f(−1)=5\).
\[\begin{align} \text{AROC} &= \dfrac{f(a+h)−f(a)}{h} \\ &=\dfrac{5−(−6)}{−3} \\&=\dfrac{11}{−3} \\ &=−\dfrac{11}{3} \end{align}\]
Вправа\(\PageIndex{1}\)
Знайти середню швидкість зміни, що з'єднує точки\((−5,1.5)\) і\((−2.5,9)\)
Рішення
3
Розуміння миттєвої швидкості змін
Тепер, коли ми можемо знайти середню швидкість зміни, припустимо, що ми робимо\(h\) на малюнку\(\PageIndex{2}\) менше і менше. Потім\(a+h\) буде\(a\) наближатися як\(h\) стає менше, все ближче і ближче до 0. Точно так само і другий пункт\((a+h,f(a+h))\) буде наближатися до першого пункту,\((a,f(a))\). Як наслідок, сполучна лінія між двома точками, звана січною лінією, буде ставати все ближче і ближче до того, щоб бути дотичною до функції в\(x=a\), а нахил січної лінії буде все ближче і ближче до нахилу дотичної в\(x=a\) (рис.\(\PageIndex{3}\)).
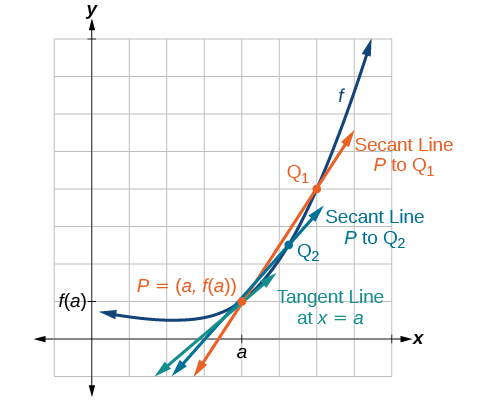
Оскільки ми шукаємо нахил дотичної в\(x=a\), ми можемо думати про міру нахилу кривої функції\(f\) в даній точці як швидкість зміни в конкретний момент. Ми називаємо цей нахил миттєвою швидкістю зміни, або похідну функції на\(x=a.\) обох можна знайти, знайшовши межу нахилу прямої, що з'єднує точку в\(x=a\) з другою точкою, нескінченно закритою вздовж кривої. Для функції як миттєва швидкість зміни функції,\(f\) так і похідна функції at\(x=a\) записуються як\(f'(a),\) і ми можемо визначити їх як двосторонню межу, яка має однакове значення незалежно від того, наближається зліва чи справа.
\[f′(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h}\]
Вираз, за допомогою якого знайдено межу, відомий як різницевий коефіцієнт.
ВИЗНАЧЕННЯ МИТТЄВОЇ ШВИДКОСТІ ЗМІНИ ТА ПОХІДНОЇ
Похідна, або миттєва швидкість зміни функції\(f\) at\(x=a\), задається
\[ f'(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h}\]
Вираз\(\frac{f(a+h)−f(a)}{h}\) називається різницевим коефіцієнтом.
Використовується різницевий коефіцієнт для оцінки межі швидкості зміни функції як\(h\) наближається до 0.
Похідні: тлумачення та позначення
Похідна функції може інтерпретуватися по-різному. Його можна спостерігати як поведінку графіка функції або розраховувати як числову швидкість зміни функції.
- Похідна функції\(f(x)\) в точці\(x=a\) - це нахил дотичної лінії до кривої\(f(x)\) в\(x=a\). Пишуть похідну\(x=a\) від\(f(x)\) at\(f′(a)\).
- Похідна\(f′(a)\) вимірює, як змінюється крива в точці\((a,f(a))\).
- Похідна\(f′(a)\) може розглядатися як миттєва швидкість зміни функції\(f(x)\) при\(x=a\).
- Якщо функція вимірює відстань як функцію часу, то похідна вимірює миттєву швидкість в часі\(t=a\).
ПОЗНАЧЕННЯ ДЛЯ ПОХІДНОЇ
Рівняння похідної функції\(f(x)\) записується як\(y′=f′(x)\), де\(y=f(x)\). Позначення\(f′(x)\) читається як «\(f\)просте з»\(x\). Альтернативні позначення для похідної включають наступне:
\[f′(x)=y′=\dfrac{dy}{dx}=\dfrac{df}{dx}=\dfrac{d}{dx} f(x)=Df(x)\]
Вираз тепер\(f′(x)\) є функцією\(x\); ця функція дає нахил кривої\(y=f(x)\) при будь-якому значенні\(x\). \(x=a\)Позначається похідна функції\(f(x)\) в точці\(f′(a)\).
how to: Задано функцію\(f\), find the derivative by applying the definition of the derivative.
- Розрахувати\(f(a+h)\).
- Розрахувати\(f(a)\).
- Підставляємо і спрощуємо\(\frac{f(a+h)−f(a)}{h}\).
- Оцініть ліміт, якщо він існує:\(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}\).
Приклад\(\PageIndex{1}\): Finding the Derivative of a Polynomial Function
Знайти похідну від функції\(f(x)=x^2−3x+5\) при\(x=a.\)
Рішення
У нас є:
\[ f′(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \;\;\;\;\;\;\;\; \text{Definition of a derivative}\]
Замінник\(f(a+h)=(a+h)^2−3(a+h)+5\) і\(f(a)=a^2−3a+5.\)
\[ \begin{align} f′(a) &= \lim \limits_{h \to 0} \dfrac{(a+h)(a+h)−3(a+h)+5−(a^2−3a+5)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{a^2+2ah+h^2−3a−3h+5−a^2+3a−5}{h} && \text{Evaluate to remove parentheses.} \\ & = \lim \limits_{h \to 0} \dfrac{\cancel{a^2}+2ah+h^2−\cancel{3a}−3h+\cancel{5}−\cancel{a^2}+\cancel{3a}−\cancel{5}}{h} && \text{Simplify.} \\ & = \lim \limits_{h \to 0} \dfrac{2ah+h^2−3h}{h} && \text{Factor out an }h. \\ & =2a+0−3 && \text{Evaluate the limit.} \\ &=2a−3 \end{align} \]
Вправа\(\PageIndex{1}\)
Знайти похідну від функції\(f(x)=3x^2+7x\) при\(x=a\)
Рішення
\(f′(a)=6a+7\)
Пошук похідних від раціональних функцій
Щоб знайти похідну від раціональної функції, ми іноді спростимо вираз за допомогою алгебраїчних прийомів, які ми вже вивчили.
Приклад\(\PageIndex{1}\): Finding the Derivative of a Rational Function
Знайти похідну від функції\(f(x)=\dfrac{3+x}{2−x}\) при\(x=a.\)
\[\begin{align} f′(a) &= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{\frac{3+(a+h)}{2−(a+h)}−(\frac{3+a}{2−a})}{h} && \text{Substitute }f(a+h) \text{ and }f(a) \\ &= \lim \limits_{h \to 0} \dfrac{(2−(a+h))(2−a)[ \frac{3+(a+h)}{2−(a+h)}−(\frac{3+a}{2−a}) ]}{(2−(a+h))(2−a)(h)} && \text{Multiply numerator and denominator by } (2−(a+h))(2−a) \\ & =\lim \limits_{h \to 0}\dfrac{(\cancel{2−(a+h)})(2−a)(\frac{3+(a+h)}{\cancel{(2−(a+h))}})−(2−(a+h))\cancel{(2−a)}(\frac{3+a}{\cancel{2−a}})}{(2−(a+h))(2−a)(h)} && \text{Distribute} \\ & =\lim \limits_{h \to 0} \dfrac{6−3a+2a−a^2+2h−ah−6+3a+3h−2a+a^2+ah}{(2−(a+h))(2−a)(h)} && \text{Multiply} \\ &=\lim \limits_{h \to 0} \dfrac{5 \cancel{h}}{(2−(a+h))(2−a)(\cancel{h})} && \text{Combine like terms} \\ & = \lim \limits_{h \to 0} \dfrac{5}{(2−(a+h))(2−a)} && \text{Cancel like factors} \\ & =\dfrac{5}{(2−(a+0))(2−a)}=\dfrac{5}{(2−a)(2−a)}=\dfrac{5}{(2−a)^2} && \text{Evaluate the limit} \end{align}\]
Вправа\(\PageIndex{1}\):
Знайти похідну функції за\(f(x)=\frac{10x+11}{5x+4}\) адресою\(x=a\).
\[f′(a)=\dfrac{−15}{(5a+4)^2}\]
Пошук похідних функцій з коренями
Щоб знайти похідні функцій з коренями, ми використовуємо методи, які ми навчилися знаходити межі функцій з коренями, в тому числі множення на кон'югат.
Приклад\(\PageIndex{1}\): Finding the Derivative of a Function with a Root
Знайти похідну від функції\(f(x)=4\sqrt{x}\) при\(x=36.\)
У нас є
\[\begin{align} f′(a) &=\lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{4\sqrt{a+h}−4\sqrt{a}}{h} && \text{Substitute }f(a+h) \text{ and }f(a) \end{align}\]
Помножте чисельник і знаменник на сполучений:\(\frac{4\sqrt{a+h}+4\sqrt{a}}{4\sqrt{a+h}+4\sqrt{a}}\).
\[\begin{align} f′(a) &= \lim \limits_{h \to 0}\bigg( \dfrac{4\sqrt{a+h}−4\sqrt{a}}{h} \bigg)⋅ \bigg(\dfrac{4\sqrt{a+h}+4\sqrt{a}}{4\sqrt{a+h}+4\sqrt{a}} \bigg) \\ &=\lim \limits_{h \to 0} \bigg( \dfrac{16(a+h)−16a}{h4(\sqrt{a+h}+4\sqrt{a})} \bigg) && \text{Multiply.} \\ &=\lim \limits_{ h \to 0} \bigg( \dfrac{\cancel{16a}+16h\cancel{−16a}}{h4(\sqrt{a+h}+4\sqrt{a})} \bigg) && \text{Distribute and combine like terms.} \\ &= \lim \limits_{h \to 0}\bigg(\dfrac{16\cancel{h}}{\cancel{h}(4\sqrt{a+h}+4\sqrt{a})} \bigg) && \text{Simplify.} \\ & = \lim \limits_{h \to 0} \bigg( \dfrac{16}{4\sqrt{a+h}+4\sqrt{a}} \bigg) && \text{Evaluate the limit by letting } h=0. \\ & =\dfrac{16}{8\sqrt{a}}=\dfrac{2}{\sqrt{a}} \\ f′(36) &= \dfrac{2}{\sqrt{36}} && \text{Evaluate the derivative at } x=36. \\ &=\dfrac{2}{6} \\ & =\dfrac{1}{3} \end{align}\]
Вправа\(\PageIndex{1}\):
Знайти похідну від функції\(f(x)=9\sqrt{x}\) при\(x=9.\)
\(\frac{3}{2}\)
Пошук миттєвих темпів змін
Багато застосувань похідної передбачають визначення швидкості зміни в даний момент функції з незалежним змінним часом - саме тому використовується термін миттєвий. Розглянемо висоту м'яча, кинутого вгору з початковою швидкістю 64 футів в секунду, задана\(s(t)=−16t^2+64t+6\), де\(t\) вимірюється в секундах і\(s(t)\) вимірюється в футах. Ми знаємо, що шлях - це парабола. Похідна розповість нам, як змінюється висота в будь-який момент часу. Висота кулі показана на малюнку як функція часу. У фізиці ми називаємо це «s - t графом».
Приклад\(\PageIndex{1}\): Finding the Instantaneous Rate of Change
Використовуючи функцію вище\(s(t)=−16t^2+64t+6\), яка миттєва швидкість кулі в 1 секунду і 3 секунди в його польоті?
Швидкість при\(t=1\) і\(t=3\) - це миттєва швидкість зміни відстані за час, або швидкість. Зверніть увагу, що початкова висота становить 6 футів. Щоб знайти миттєву швидкість, знаходимо похідну і оцінюємо її при\(t=1\) і\(t=3\):
\[\begin{align} f′(a) &= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{−16(t+h)^2+64(t+h)+6−(−16t^2+64t+6)}{h} && \text{Substitute } s(t+h) \text{ and } s(t). \\ &= \lim \limits_{h \to 0} \dfrac{−16t^2−32ht−h^2+64t+64h+6+16t^2−64t−6}{h} && \text{Distribute} \\ & =\lim \limits_{h \to 0} \dfrac{−32ht−h^2+64h}{h} && \text{Simplify.} \\ &= \lim \limits_{h \to 0} \dfrac{\cancel{h}(−32t−h+64)}{\cancel{h}} && \text{Factor the numerator.} \\ & =\lim \limits_{h \to 0}−32t−h+64 && \text{ Cancel out the common factor} h. \\ s′(t) &=−32t+64 && \text{Evaluate the limit by letting} h=0. \end{align}\]
Для будь-якого значення\(t\),\(s′(t)\) говорить нам швидкість при цьому значенні\(t\).
Оцініть\(t=1\) і\(t=3\).
\[\begin{align}s′(1) &=−32(1)+64=32 \\ s′(3) &=−32(3)+64=−32 \end{align}\]
Швидкість м'яча через 1 секунду становить 32 фути в секунду, оскільки він знаходиться на шляху вгору.
Швидкість м'яча через 3 секунди становить −32 фути в секунду, оскільки він знаходиться на шляху вниз.
Вправа\(\PageIndex{1}\):
Положення м'яча задається\(s(t)=−16t^2+64t+6.\) Яка його швидкість 2 секунди в польоті?
0
Використання графіків для пошуку миттєвих темпів зміни
Ми можемо оцінити миттєву швидкість зміни при\(x=a\) спостереженні нахилу кривої функції\(f(x)\) в\(x=a\). Ми робимо це, намалювавши лінію, дотичну до функції at\(x=a\) і знайшовши її нахил.
how to: Задано графік функції\(f( x )\), find the instantaneous rate of change of the function at \(x=a\).
- Знайдіть\(x=a\) на графіку функції\(f(x)\).
- Намалюйте дотичну лінію, лінію, яка проходить\(x=a\) в\(a\) будь-якій іншій точці кривої та не в ній. Простягніть лінію досить далеко, щоб обчислити її нахил як
\[\dfrac{\text{change in }y}{\text{change in }x.}\]
Приклад\(\PageIndex{1}\): Estimating the Derivative at a Point on the Graph of a Function
З графіка функції,\(y=f(x)\) представленого на малюнку, оцініть кожне з наступних дій:
\(f(0) ; f(2) ; f'(0) ; f'(2)\)
Щоб знайти функціональне значення\(f(a)\), знайдіть y -координату at\(x=a\).
Щоб знайти похідну при\(x=a, f′(a),\) малюванні дотичної лінії\(x=a,\) і оцінити нахил цієї дотичної лінії. Див. Малюнок.
- \(f(0)\)є y -координата at\(x=0\). Точка має координати\((0,1)\), таким чином\(f(0)=1\).
- \(f(2)\)є y -координата at\(x=2\). Точка має координати\((2,1)\), таким чином\(f(2)=1\).
- \(f′(0)\)знаходить шляхом оцінки нахилу дотичної лінії до кривої в\(x=0\). Дотична лінія до кривої на\(x=0\) виглядає горизонтальною. Горизонтальні лінії мають нахил 0, таким чином\(f′(0)=0\).
- \(f′(2)\)знаходить шляхом оцінки нахилу дотичної лінії до кривої в\(x=2\). Спостерігайте за шляхом дотичної лінії до кривої на\(x=2\). Коли\(x\) значення рухається на одну одиницю вправо,\(y\) значення рухається вгору на чотири одиниці в іншу точку на лінії. Таким чином, ухил дорівнює 4, так\(f′(2)=4\).
Вправа\(\PageIndex{1}\):
Використовуючи графік функції,\(f(x)=x^3−3x\) показаний на малюнку, оцінюємо:\(f(1), f′(1), f(0)\), і\(f′(0)\).
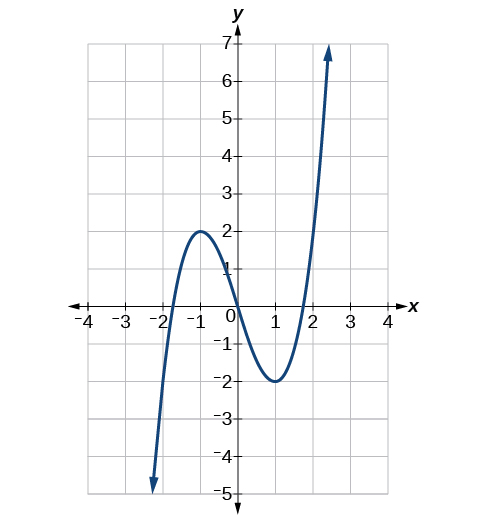
−2, −2,0, 0, −3
Використання миттєвих темпів змін для вирішення реальних проблем
Інший спосіб інтерпретувати миттєву швидкість зміни в\(x=a\) - це спостереження за функцією в реальному контексті. Одиницею для похідної функції\(f(x)\) є
\[\dfrac{\text{output units}}{\text{input unit}}\]
Така одиниця показує, на скільки одиниць змінюється вихід за кожну одиницю зміни вхідного сигналу. Миттєва швидкість зміни в даний момент показує те ж саме: одиниці зміни виходу на одиницю зміни вхідного сигналу.
Одним із прикладів миттєвої швидкості зміни є гранична вартість. Наприклад, припустимо, що виробничі витрати компанії на\(C(x)\) виробництво\(x\) предметів дається в тисячах доларів. Похідна функція говорить нам, як змінюється вартість для будь-якого значення\(x\) в області функції. Іншими словами,\(C′(x)\) трактується як гранична вартість, додаткові витрати в тисячах доларів виробництва ще одного товару, коли\(x\) товари були виготовлені. Наприклад,\(C′(11)\) це приблизна додаткова вартість в тисячах доларів виробництва 12-ї позиції після того, як 11 найменувань були виготовлені. \(C′(11)=2.50\)означає, що коли 11 одиниць були виготовлені, виробництво 12-го елемента збільшить загальну вартість приблизно на 2500.00 доларів.
Приклад\(\PageIndex{1}\): Finding a Marginal Cost
Вартість в доларах виробництва\(x\) портативних комп'ютерів в доларах є\(f(x)=x^2−100x.\) У точці, де було випущено 200 комп'ютерів, яка приблизна вартість виробництва 201 одиниці?
Якщо\(f(x)=x^2−100x\) описується вартість виробництва\(x\) комп'ютерів,\(f′(x)\) опишемо граничну вартість. Нам потрібно знайти похідну. Для цілей обчислення похідної ми можемо використовувати наступні функції:
\[\begin{align} f(a+b) &=(x+h)^2−100(x+h) \\ f(a) &=a ^2−100a \end{align}\]
\[\begin{align} f′(x) &=\dfrac{f(a+h)−f(a)}{h} && \text{Formula for a derivative} \\ &=\dfrac{(x+h)^2−100(x+h)−(x^2−100x)}{h} \\ \text{Substitute }f(a+h) \text{ and }f(a). \\ & =\dfrac{x^2+2xh+h^2−100x−100h−x^2+100x}{h} && \text{Multiply polynomials, distribute.} \\ &= \text{2xh+h^2−100h}{h} && \text{Collect like terms.} \\ &=\dfrac{\cancel{h}(2x+h−100)}{\cancel{h}} && \text{Factor and cancel like terms.} \\ &=2x+h−100 && \text{Simplify.} \\ &=2x−100 && \text{Evaluate when }h=0. \\ f′(x) &=2x−100 && \text{Formula for marginal cost} \\ f′(200) &=2(200)−100=300 && \text{Evaluate for 200 units.} \end{align}\]
Гранична вартість виробництва 201 одиниці становитиме приблизно 300 доларів.
Приклад\(\PageIndex{1}\):Interpreting a Derivative in Context
Автомобіль виїжджає з перехрестя. Відстань, яку вона проходить у милі, задається функцією\( f(t)\), де\(t\) представляє години. Поясніть наступні позначення:
\(f(0)=0 f′(1)=60 f(1)=70 f(2.5)=150\)
Спочатку нам потрібно оцінити функцію\(f(t)\) і похідну функції\(f′(t)\), і розрізнити їх між ними. Коли ми оцінюємо функцію\(f(t)\), ми знаходимо відстань, яку автомобіль пройшов за\(t\) годинами. Коли ми оцінюємо похідну f′ (t), f′ (t), ми знаходимо швидкість автомобіля після\(t\) години.
- \(f(0)=0\)означає, що за нульові години автомобіль проїхав нуль миль.
- \(f′(1)=60\)означає, що через годину в поїздці автомобіль їде 60 миль на годину.
- \(f(1)=70\)означає, що за годину до поїздки автомобіль проїхав 70 миль. У якийсь момент протягом першої години, потім, автомобіль, мабуть, їхав швидше, ніж був на 1-годинній позначці.
- \(f(2.5)=150\)означає, що за дві години тридцять хвилин до поїздки автомобіль проїхав 150 миль.
Вправа\(\PageIndex{1}\)
Бігун біжить по прямій дорозі схід-захід. Функція\(f(t)\) дає, скільки футів на схід від своєї початкової точки вона знаходиться через\(t\) секунди. Інтерпретуйте кожне з наступних дій, як це стосується бігуна.
\(f(0)=0 ; f(10)=150 ; f′(10)=15 ; f′(20)=−10 ; f(40)=−100\)
- Через нуль секунд вона пройшла 0 футів.
- Через 10 секунд вона подорожувала 150 футів на схід.
- Через 10 секунд вона рухається на схід зі швидкістю 15 футів/сек.
- Через 20 секунд вона рухається на захід зі швидкістю 10 футів/сек.
- Через 40 секунд вона знаходиться на 100 футах на захід від своєї відправної точки.
Пошук точок, де похідна функції не існує
Щоб зрозуміти, де похідна функції не існує, нам потрібно згадати, що зазвичай відбувається, коли функція\(f(x)\) має похідну at\(x=a\). Припустимо, ми використовуємо графічну утиліту для збільшення масштабу\(x=a\). Якщо функція\(f(x)\) диференційована, тобто якщо це функція, яку можна диференціювати, то чим ближче збільшується, тим ближче графік наближається до прямої. Ця характеристика називається лінійністю.
Подивіться на графік на малюнку. Чим ближче ми збільшуємо масштаб точки, тим більш лінійною виглядає крива.
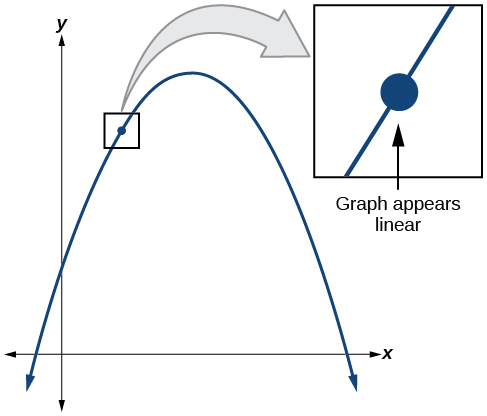
Графік функції\(f(x)=| x |\), з віссю x від —0,1 до 0,1 та осі y від —0,1 до 0,1.
Які характеристики графіка, який не диференціюється в точці? Ось кілька прикладів, в яких функція\(f(x)\) не диференційовна на\(x=a\).
На малюнку ми бачимо графік
\[f(x)=\begin{cases} x^2, &&x≤2 \\ 8−x, &&x>2.\end{cases} .\]
Зверніть увагу, що при\(x\) підходах 2 зліва ліва межа може спостерігатися рівною 4, тоді як при\(x\) підходах 2 праворуч може спостерігатися праворуч межа 6. Ми бачимо, що він має розрив при\(x=2\).
Графік\(f(x)\) має розрив при\(x=2\).
На малюнку ми бачимо графік\(f(x)=|x|\). Ми бачимо, що графік має кутову точку в\(x=0\).
Графік\(f(x)=| x |\) має кутову точку в\(x=0\).
На малюнку ми бачимо, що графік\(f(x)=x^{\frac{2}{3}}\) має крок на\(x=0\). Кап має унікальну особливість. Відходячи від перевороту, як ліва, так і права межі наближаються або до нескінченності, або негативної нескінченності. Зверніть увагу, що дотичні лінії,\(x\) коли наближається 0 як зліва, так і справа, здається, стають все більш крутішими, але один має негативний нахил, інший має позитивний нахил.
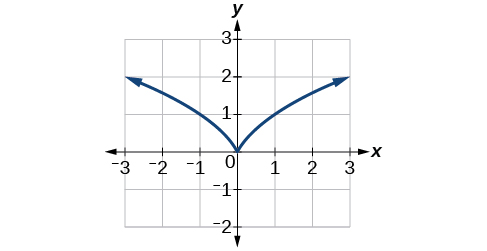
Графік\(f(x)=x^\frac{2}{3}\) має розріз в\(x=0\).
На малюнку ми бачимо, що граф\(f(x)=x^{frac{1}{3}}\) має вертикальну дотичну в\(x=0\). Нагадаємо, що вертикальні дотичні - це вертикальні лінії, тому там, де існує вертикальний тангенс, нахил лінії невизначений. Ось чому похідної, яка вимірює ухил, там не існує.

Графік\(f(x)=x^\frac{1}{3}\) має вертикальну дотичну в\(x=0\).
диференційованість
\(f(x)\)Функція диференційовна,\(x=a\) якщо похідна існує в\(x=a\), що означає, що\(f′(a)\) існує.
Існує чотири випадки, для яких функція\(f(x)\) не диференційована в точці\(x=a\).
- Коли відбувається розрив при\(x=a\).
- Коли є кутова точка на\(x=a\).
- Коли є порізка при\(x=a\).
- Будь-який інший час, коли є вертикальний тангенс в\(x=a\).
Приклад\(\PageIndex{1}\): Determining Where a Function Is Continuous and Differentiable from a Graph
Використовуючи Figure, визначте, де знаходиться функція
- безперервний
- переривчастий
- диференційований
- не диференційований
У точках, де графік є переривчастим або не диференційованим, вкажіть чому.
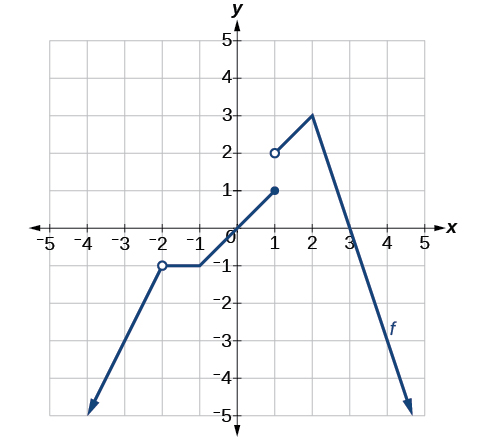
Три інтервали, де функція безперервна
Графік диференційований на\((−∞,−2)∪(−2,−1)∪(−1,1)∪(1,2)∪(2,∞)\). Графік не диференціюється в\(x=−2\) тому, що це точка розриву, в\(x=−1\) через гострий кут, в\(x=1\) тому що це точка розриву, і\(x=2\) через гострий кут.\(f(x)\) Див. Малюнок.
П'ять інтервалів, де функція диференційована
Вправа\(\PageIndex{1}\):
Визначте, де функція,\(y=f(x)\) показана на малюнку, є безперервною і диференційованою від графіка.
Графік\(f\) неперервний на\((−∞,1)∪(1,3)∪(3,∞).\) Графік f f є переривчастим в\(x=1\) а\(x=3\). Графік\(f\) диференційовний на\((−∞,1)∪(1,3)∪(3,∞)\). Графік не\(f\) диференційовний при\(x=1\) і\(x=3\).
Пошук рівняння прямої дотичної до графа функції
Рівняння дотичної лінії до кривої функції\(f(x)\) at\(x=a\) походить від точково-нахилу форми прямої,\(y=m(x−x_1)+y_1\). Нахил прямої - це нахил кривої в\(x=a\) і, отже, дорівнює\(f′(a),\)\(x=a.\) похідній\(f(x)\) at Координатна пара точки на лінії в\(x=a\) є\((a,f(a))\).
Якщо ми підставимо в точку-нахил форми, ми маємо
Рівняння дотичної прямої дорівнює
\[y=f'(a)(x−a)+f(a)\]
F
Рівняння прямої дотичної до кривої функції\(f\) в точці\(x=a\) дорівнює
\[y=f'(a)(x−a)+f(a)\]
how to: Задано функцію\(f\), find the equation of a line tangent to the function at \(x=a\).
- Знайти похідну від\(f(x)\) at\(x=a\) використання\(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}.\)
- Оцініть функцію за адресою\(x=a\). Це\(f(a)\).
- \(f′(a)\)Підставляємо\((a,f(a))\) і в\(y=f'(a)(x−a)+f(a)\).
- Запишіть рівняння дотичної прямої у вигляді\(y=mx+b\).
Приклад\(\PageIndex{1}\): Finding the Equation of a Line Tangent to a Function at a Point
Знайти рівняння прямої дотичної до кривої\(f(x)=x^2−4x\) при\(x=3.\)
Використання:
\[f'(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h}\]
Замінник\(f(a+h)=(a+h)^2−4(a+h)\) і\(f(a)=a^2−4a.\)
\[\begin{align} f′(a) &= \lim \limits_{h \to 0}\dfrac{(a+h)(a+h)−4(a+h)−(a2−4a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{a^2+2ah+h^2−4a−4h−a^2+4a}{h} && \text{Remove parentheses.} \\ &= \lim \limits_{h \to 0} \dfrac{\cancel{a^2}+2ah+h^2−\cancel{4a}−4h−\cancel{a^2}+\cancel{4a}}{h} && \text{Combine like terms.} \\ &= \lim \limits_{h \to 0} \dfrac{2ah+h^2−4h}{h} \\ &= \lim \limits_{h \to 0} \dfrac{\cancel{h}(2a+h−4)}{h} && \text{Factor out }h. \\ &=2a+0−4 \\ f′(a)&=2a−4 && \text{Evaluate the limit.} \\ f′(3)&=2(3)−4=2 \end{align}\]
Рівняння дотичної прямої при\(x=3\):
\[\begin{align} y &= f'(a)(x−a)+f(a) \\ y &=f'(3)(x−3)+f(3) \\ y &=2(x−3)+(−3) \\ y &=2x−9 \end{align}\]
Аналіз
Ми можемо використовувати графічну утиліту для графіків функції та дотичної лінії. При цьому ми можемо спостерігати точку дотику в,\(x=3\) як показано на малюнку.
Графік підтверджує точку дотику в\(x=3\).
Вправа\(\PageIndex{1}\):
Знайти рівняння дотичної прямої до кривої функції\(f(x)=5x^2−x+4\) в\(x=2\).
\(y=19x−16\)
Пошук миттєвої швидкості частинки
Якщо функція вимірює положення проти часу, похідна вимірює зміщення проти часу або швидкість об'єкта. Зміна швидкості або напрямку відносно зміни часу відома як швидкість. Швидкість в даний момент відома як миттєва швидкість.
Намагаючись знайти швидкість або швидкість об'єкта в даний момент, ми, здається, стикаємося з протиріччям. Зазвичай ми визначаємо швидкість як пройдену відстань, розділену на минулий час. Але в одну мить не проїжджається відстань, і часу не проходить. Як розділимо нуль на нуль? Використання похідної вирішує цю проблему. Похідна дозволяє сказати, що навіть поки швидкість об'єкта постійно змінюється, вона має певну швидкість в даний момент. Це означає, що якби об'єкт подорожував з такою точною швидкістю протягом одиниці часу, він проїхав би задану відстань.
МИТТЄВА ШВИДКІСТЬ
Нехай функція\(s(t)\) представляє положення об'єкта в час\(t.\) Миттєва швидкість або швидкість об'єкта в час\(t=a\) задається
\[s′(a)= \lim \limits_{h \to 0} \dfrac{s(a+h)−s(a)}{h}\]
Приклад\(\PageIndex{1}\): Finding the Instantaneous Velocity
М'яч кидається вгору з висоти 200 футів з початковою швидкістю 36 футів/сек. Якщо висота м'яча в футах через\(t\) секунди задається,\(s(t)=−16t^2+36t+200,\) знайдіть миттєву швидкість м'яча при\( t=2\).
По-перше, ми повинні знайти похідну\(s′(t)\). Потім оцінюємо похідну при\(t=2\), використовуючи\(s(a+h)=−16(a+h)^2+36(a+h)+200\) і\(s(a)=−16a^2+36a+200.\)
\[\begin{align} s′(a)= \lim \limits_{h \to 0} \dfrac{s(a+h)−s(a)}{h} \\ &= \lim \limits_{h \to 0}\dfrac{−16(a+h)^2+36(a+h)+200−(−16a^2+36a+200)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{−16(a^2+2ah+h^2)+36(a+h)+200−(−16a^2+36a+200)}{h} \\ &= \lim \limits_{h \to 0}\dfrac{−16a^2−32ah−16h^2+36a+36h+200+16a^2−36a−200}{h} \\ &= \lim \limits_{h \to 0}\dfrac{\cancel{−16a^2}−32ah−16h^2+\cancel{36a}+36h+\cancel{200}+\cancel{16a^2}−\cancel{36a}−\cancel{200}}{h} \\ &= \lim \limits_{h \to 0}\dfrac{−32ah−16h^2+36h}{h} \\ &= \lim \limits_{h \to 0}\dfrac{\cancel{h}(−32a−16h+36)}{\cancel{h}} \\ &= \lim \limits_{h \to 0}(−32a−16h+36) \\&=−32a−16⋅0+36 \\ s′(a) &=−32a+36 \\ s′(2) &=−32(2)+36 \\ & =−28 \end{align}\]
Аналіз
Цей результат означає, що в\(t=2\) секунди часу м'яч опускається зі швидкістю 28 футів/сек.
Вправа\(\PageIndex{1}\):
Ракета-феєрверк вистрілюється вгору з ями на 12 футів під землею зі швидкістю 60 футів/сек. Його висота в ногах через\(t\) секунди задається\(s=−16t^2+60t−12.\) Яка його миттєва швидкість через 4 секунди?
—68 футів/сек, він опускається назад на Землю зі швидкістю 68 футів/с.
Отримайте доступ до цих онлайн-ресурсів для додаткової інструкції та практики з похідними.
Відвідайте цей веб-сайт для додаткових питань практики від Learningpod.
Ключові рівняння
| середня швидкість зміни | \(\text{AROC}=\frac{f(a+h)−f(a)}{h}\) |
| похідна функції | \(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}\) |
Ключові поняття
- Нахил січної лінії, що з'єднує дві точки, є середньою швидкістю зміни функції між цими точками. Див. Приклад.
- Похідна, або миттєва швидкість зміни, - це міра нахилу кривої функції в заданій точці або нахилу прямої дотичної до кривої в цій точці. Див. розділ Приклад , Приклад та Приклад.
- Коефіцієнт різниці - це частка у формулі миттєвої швидкості зміни:
\(\frac{f(a+h)−f(a)}{h}\)
- Миттєві темпи змін можуть бути використані для пошуку рішень багатьох реальних проблем. Див. Приклад.
- Миттєву швидкість зміни можна знайти, спостерігаючи нахил функції в точці на графіку, намалювавши лінію, дотичну до функції в цій точці. Див. Приклад.
- Миттєві темпи змін можуть бути інтерпретовані для опису реальних ситуацій. Див. Приклад і Приклад.
- Деякі функції не диференційовані в точці або точках. Див. Приклад.
- Точка-нахил форми прямої може бути використана для пошуку рівняння прямої дотичної до кривої функції. Див. Приклад.
- Швидкість - це зміна положення щодо часу. Миттєва швидкість описує швидкість об'єкта в даний момент. Середня швидкість описує швидкість, що підтримується протягом проміжку часу.
- Використання похідної дає можливість обчислити миттєву швидкість, навіть якщо немає витраченого часу. Див. Приклад.
Розділ вправи
Вербальний
Як нахил лінійної функції подібний до похідної?
Нахил лінійної функції залишається однаковим. Похідна загальної функції варіюється в залежності від\(x\). Як нахил прямої, так і похідна в точці вимірюють швидкість зміни функції.
У чому різниця між середньою швидкістю зміни функції на інтервалі\([ x,x+h ]\) та похідною функції при\(x\)?
Автомобіль проїхав 110 миль за період часу з 14:00 до 16:00 Яка середня швидкість автомобіля? Рівно о 14:30 швидкість автомобіля зареєструвала рівно 62 милі на годину. Як інша назва швидкості автомобіля о 14:30? Чому ця швидкість відрізняється від середньої швидкості?
Середня швидкість - 55 миль на годину. Миттєва швидкість о 14:30 - 62 милі на годину. Миттєва швидкість вимірює швидкість автомобіля в один момент часу, тоді як середня швидкість дає швидкість автомобіля протягом інтервалу.
Поясніть поняття нахилу кривої в точці\(x\).
Припустимо, вода надходить в резервуар з середньою швидкістю 45 галонів в хвилину. Переведіть це твердження на мову математики.
Середня швидкість зміни кількості води в резервуарі становить 45 галонів в хвилину. Якщо\(f(x)\) є функція, що дає кількість води в баку в будь-який час\(t\), то середня швидкість зміни\(f(x)\) між\(t=a\) і\(t=b\) становить\(f(a)+45(b−a).\)
алгебраїчна
Для наступних вправ використовуйте визначення похідної\(\lim \limits_{h to 0} \frac{f(x+h)−f(x)}{h}\) для обчислення похідної кожної функції.
\(f(x)=3x−4\)
\(f(x)=−2x+1\)
\(f′(x)=−2\)
\(f(x)=x^2−2x+1\)
\ (f (x) = 2x^2+x−3
\(f′(x)=4x+1\)
\(f(x)=2x^2+5\)
\(f(x)=\frac{−1}{x−2}\)
\(f′(x)=\frac{1}{(x−2)^2}\)
\(f(x)=\frac{2+x}{1−x}\)
\(f(x)=\frac{5−2x}{3+2x}\)
\(\frac{−16(}{3+2x)^2}\)
\(f(x)=\sqrt{1+3x}\)
\(f(x)=3x^3−x^2+2x+5\)
\(f′(x)=9x^2−2x+2\)
\(f(x)=5\)
\(f(x)=5π\)
\(f′(x)=0\)
Для наступних вправ знайдіть середню швидкість зміни між двома точками.
\((−2,0)\)і\((−4,5)\)
\((4,−3)\)і\((−2,−1)\)
\(−\frac{1}{3}\)
\((0,5)\)і\((6,5)\)
\((7,−2)\)і\((7,10)\)
невизначений
Для наступних поліноміальних функцій знайдіть похідні.
\(f(x)=x^3+1\)
\(f(x)=−3x^2−7x=6\)
\(f′(x)=−6x−7\)
\(f(x)=7x^2\)
\(f(x)=3x^3+2x^2+x−26\)
\(f′(x)=9x^2+4x+1\)
Для наступних функцій знайдіть рівняння дотичної лінії до кривої в заданій точці\(x\) на кривій.
\(f(x)=2x^2−3x \;\;\; x=3\)
\(f(x)=x^3+1 \;\;\;\; x=2\)
\(y=12x−15\)
\(f(x)=\sqrt{x} \;\;\;\; x=9\)
Для наступної вправи знайдіть\(k\) таке, щоб задана лінія була дотичною до графіка функції.
\(f(x)=x^2−kx, \;\;\; y=4x−9\)
\(k=−10\)або\(k=2\)
Графічний
Для наступних вправ розглянемо графік функції\(f\) та визначаємо, де функція є безперервною/розривною та диференційованою/не диференційованою.
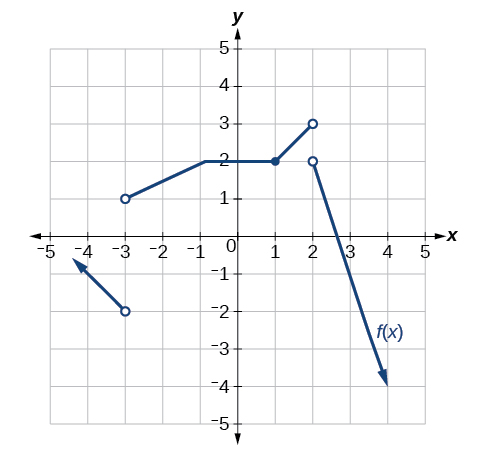
\(x=−2\)Переривчастий при і\(x=0\). Не диференціюється при —2, 0, 2.
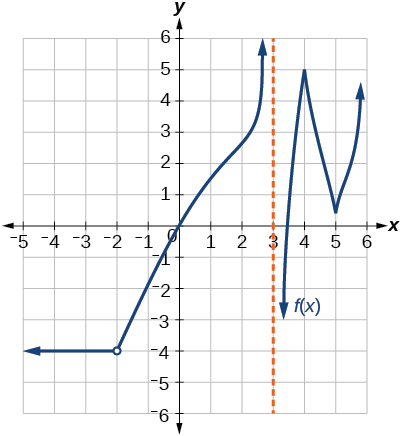
Розрив при\(x=5\). Не диференціюється при -4, —2, 0, 1, 3, 4, 5.
Для наступних вправ використовуйте Figure для оцінки функції за заданим значенням\(x\) або похідною при заданому значенні\(x\), як зазначено.
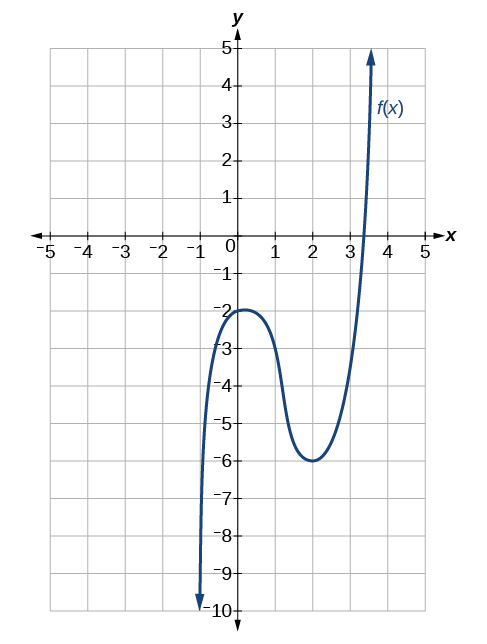
\(f(−1)\)
\(f(0)\)
\(f(0)=−2\)
\(f(1)\)
\(f(2)\)
\ (f (2) =−6f (2) =−6
\(f(3)\)
\(f′(−1)\)
\(f′(−1)=9\)
\(f′(0)\)
\(f′(1)\)
\(f′(1)=−3\)
\(f′(2)\)
\(f′(3)\)
\(f′(3)=9\)
Намалюйте функцію на основі наведеної нижче інформації:
\(f′(x)=2x, f(2)=4\)
Технологія
Чисельно оцінюємо похідну. Дослідіть поведінку графіка\(f(x)=x^2\) навколо\(x=1\), побудувавши функцію на наступних областях:\([ 0.9,1.1 ], [ 0.99,1.01 ], [ 0.999,1.001 ],\) і\([0.9999, 1.0001]\). Ми можемо використовувати функцію на нашому калькуляторі, яка автоматично встановлює Ymin та Ymax для встановлених нами значень Xmin та Xmax. (На деяких часто використовуваних графічних калькуляторах ця функція може називатися ZOOM FIT або ZOOM AUTO). Вивчаючи відповідні значення діапазону для цього вікна перегляду, наближають, як змінюється крива при цьому\(x=1,\), наближають похідну при\(x=1.\)
Відповіді різняться. Нахил дотичної лінії поблизу\(x=1\) дорівнює 2.
Реальні програми
Для наступних вправ поясніть позначення словами. \(f(t)\)Обсяг бака бензину, в галонів,\(t\) хвилин після полудня.
\(f(0)=600\)
\(f'(30)=−20\)
О 12:30, швидкість зміни кількості галонів у резервуарі становить —20 галонів на хвилину. Тобто бак втрачає 20 галонів в хвилину.
\(f(30)=0\)
\(f'(200)=30\)
Через 200 хвилин після полудня обсяг галонів в резервуарі змінюється зі швидкістю 30 галонів в хвилину.
\(f(240)=500\)
Для наступних вправ поясніть функції словами. Висота\(s\) снаряда через\(t\) секунди задається\(s(t)=−16t^2+80t.\)
\(s(2)=96\)
Висота снаряда через 2 секунди становить 96 футів.
\(s'(2)=16\)
\(s(3)=96\)
Висота снаряда в\(t=3\) секундах становить 96 футів.
\(s'(3)=−16\)
\(s(0)=0,s(5)=0.\)
Висота снаряда дорівнює нулю при\(t=0\) і знову в\(t=5\). Іншими словами, снаряд запускається на землю і знову падає на землю через 5 секунд.
Для наступних вправ\(V\) обсяг сфери щодо її радіуса\(r\) задається\(V=\frac{4}{3}πr^3.\)
Знайти середню швидкість зміни\(V\) як\(r\) зміни від 1 см до 2 см.
Знайти миттєву швидкість зміни\(V\) при r=3 см. r=3 см.
\(36π\)
Для наступних вправ дохід, отриманий від продажу\(x\) предметів, надається\(R(x)=2x^2+10x\).
Знайдіть середню зміну функції доходу у міру\(x\) зміни від\(x=10\) до\(x=20\).
Знайти\(R'(10)\) і інтерпретувати.
$50.00 за одиницю, що є миттєвою швидкістю зміни виручки, коли продаються рівно 10 одиниць.
Знайти\(R'(15)\) і інтерпретувати. Порівняйте\(R'(15)\)\(R'(10),\) і поясніть різницю.
Для наступних вправ вартість виробництва\(x\) мобільних телефонів описується функцією\(C(x)=x^2−4x+1000.\)
Знайти середню швидкість зміни загальної вартості при\(x\) зміні від\(x=10\) до\(x=15.\)
$21 за одиницю
Знайдіть приблизну граничну вартість, коли 15 мобільних телефонів були виготовлені, виробництва 16-го мобільного телефону.
Знайдіть приблизну граничну вартість, коли 20 мобільних телефонів були виготовлені, виробництва 21 st мобільний телефон.
$36
Розширення
Для наступних вправ використовуйте визначення для похідної в точці\(x=a\),\(\lim \limits_{x \to a}\frac{f(x)−f(a)}{x−a},\) щоб знайти похідну функцій.
\(f(x)=\frac{1}{x^2}\)
\(f(x)=5x^2−x+4\)
\(f'(x)=10a−1\)
\(f(x)=−x^2+4x+7\)
\(f(x)=\frac{−4}{3−x^2}\)
\(\frac{4}{(3−x)^2}\)
Розділ Огляд Вправи
Пошук меж: числовий та графічний підхід
Для виконання наступних вправ використовуйте рис.
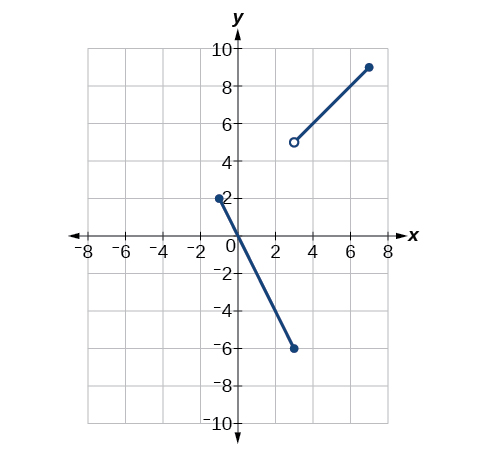
\(\lim \limits_{x \to −1^+}f(x)\)
2
\(\lim \limits_{x \to −1^−}f(x)\)
\(\lim \limits_{x \to −1} f(x)\)
не існує
\(\lim \limits_{x \to 3}f(x)\)
При яких\(x\) значеннях функції розриваються? Яка умова безперервності порушується?
Переривчастий at\(x=−1\) (\(\lim \limits_{x \to a} f(x)\)не існує),\(x=3\) (стрибок розриву), і\(x=7\) (\ lim\ limits_ {x\ to a} f (x)\) не існує).
Використання таблиці, оцінка\(\lim \limits_{x \to 0}f(x).\)
| \(x\) | \(F(x)\) |
| −0.1 | 2.875 |
| −0,01 | 2.92 |
| −0,001 | 2.998 |
| 0 | Невизначений |
| 0,001 | 2.9987 |
| 0,01 | 2.865 |
| 0.1 | 2.78145 |
| 0,15 | 2.678 |
3
Для наступних вправ із застосуванням графічної утиліти використовуйте числові або графічні докази для визначення лівої та правої меж функції, наведеної як\(x\) підходи\(a\). Якщо функція має ліміт як\(x\) підходи\(a\), вкажіть його. Якщо ні, обговоріть, чому немає меж.
\(f(x)=\begin{cases} | x |−1, && \text{if }x≠1 \\ x^3, \text{if }x=1 \end{cases} a=1\)
\(f(x)=\begin{cases} \frac{1}{x+1}, && \text{if }x=−2 \\ (x+1)^2, && \text{if }x≠−2 \end{cases} a=−2\)
\(\lim \limits_{x \to −2} f(x)=1\)
\(f(x)= \begin{cases} \sqrt{x+3} && \text{if } x < 1 \\ −\sqrt[3]{x} && \text{if }x>1 \end{cases} a=1\)
Пошук меж: властивості меж
Для наступних вправ знайдіть межі, якщо\(\lim \limits_{x \to c} f(x)=−3\) і\(\lim \limits_{x \to c} g(x)=5\).
\(\lim \limits_{x \to c} (f(x)+g(x))\)
2
\(\lim \limits_{x \to c} \frac{f(x)}{g(x)}\)
\(\lim \limits_{x to c}(f(x)⋅g(x))\)
\(−15\)
\(\lim \limits_{x \to 0^+}f(x),f(x)= \begin{cases} 3x^2+2x+1 && x>0 \\ 5x+3 && x<0 \end{cases}\)
\(\lim \limits_{x \to 0^-}f(x),f(x)= \begin{cases} 3x^2+2x+1 && x>0 \\ 5x+3 && x<0 \end{cases}\)
3
\(\lim \limits_{x \to 3^+}(3x−〚x〛)\)
Для наступних вправ оцініть межі, використовуючи алгебраїчні прийоми.
\(\lim \limits_{h \to 0}(\frac{(h+6)^2−36}{h})\)
12
\(\lim \limits_{x \to 25}(\frac{x^2−625}{\sqrt{x}−5)}\)
\(\lim \limits_{x \to 1}(\frac{−x^2−9x}{x})\)
−10
\(\lim \limits_{x \to 4}\frac{7−\sqrt{12x+1}}{x−4}\)
\(\lim \limits_{x \to −3}(\frac{\frac{1}{3}+\frac{1}{x}}{3+x})\)
\(−\frac{1}{9}\)
Безперервність
Для наступних вправ використовуйте числові докази, щоб визначити, чи існує межа на\(x=a\). Якщо немає, опишіть поведінку графіка функції за адресою\(x=a\).
\(f(x)=\frac{−2}{x−4}; a=4\)
\(f(x)=\frac{−2}{(x−4)^2}; a=4\)
При\(x=4\), функція має вертикальну асимптоту.
\(f(x)=\frac{−x}{x^2−x−6}; a=3\)
\(f(x)=\frac{6x^2+23x+20}{4x^2−25}; a=−\frac{5}{2}\)
знімний розрив при\(a=−\frac{5}{2}\)
\(f(x)=\frac{\sqrt{x}−3}{9−x}; a=9\)
Для наступних вправ визначте, де дана функція\(f(x)\) є безперервною. Там, де він не є безперервним, стан яких умов не вдається, і класифікувати будь-які розриви.
\(f(x)=x^2−2x−15\)
безперервний на\((−∞,∞)\)
\(f(x)=\frac{x^2−2x−15}{x−5}\)
\(f(x)=\frac{x^2−2x}{x^2−4x+4}\)
знімний розрив\(x=2. f(2)\) при не визначено, але межі існують.
\(f(x)=\frac{x^3−125}{2x^2−12x+10}\)
\(f(x)=\frac{x^2−\frac{1}{x}}{2−x}\)
розрив при\(x=0\) і\(x=2\). Обидва\(f(0)\) і\(f(2)\) не визначені.
\(f(x)=\frac{x+2}{x^2−3x−10}\)
\(f(x)=\frac{x+2}{x^3+8}\)
знімний розрив при\(x=–2. f(–2)\) не визначено.
похідні
Для наступних вправ знайдіть середню швидкість зміни\(\frac{f(x+h)−f(x)}{h}\).
\(f(x)=3x+2\)
\(f(x)=5\)
0
\(f(x)=\frac{1}{x+1}\)
\(f(x)= \ln (x)\)
\(\frac{\ln (x+h)− \ln (x)}{h}\)
\(f(x)=e^{2x}\)
Для наступних вправ знайдіть похідну функції.
\(f(x)=4x−6\)
\(=4\)
\(f(x)=5x^2−3x\)
Знайдіть рівняння дотичної прямої до графіка\(f(x)\) за вказаною\(x\) величиною.
\(f(x)=−x^3+4x; x=2.\)
\(y=−8x+16\)
Для наступних вправ за допомогою графічної утиліти поясніть, чому функція не диференційована скрізь у своїй області. Вкажіть точки, де функція не диференційована.
\(f(x)=\frac{x}{| x |}\)
Враховуючи, що обсяг правого кругового конуса дорівнює\(V=\frac{1}{3}πr^2h\) і що даний конус має фіксовану висоту 9 см і змінну довжину радіуса, знайдіть миттєву швидкість зміни об'єму щодо довжини радіуса, коли радіус дорівнює 2 см. Дайте точну відповідь з точки зору\(π\)
\(12π\)
Практика Тест
Для наступних вправ використовуйте графік на\(f\) малюнку.
\(f(1)\)
3
\(\lim \limits_{x \to −1^+}f(x)\)
\(\lim \limits_{x \to −1^-}f(x)\)
0
\(\lim \limits_{x \to −1}f(x)\)
\(\lim \limits_{x \to −2}f(x)\)
\(−1\)
При яких значеннях\(x\) є\(f\) переривчастим? Яке властивість наступності порушується?
Для наступних вправ із застосуванням графічної утиліти використовуйте числові або графічні докази для визначення лівої та правої меж функції, наведеної як\(x\) підходи\(a\). Якщо функція має ліміт у міру\(x\) наближення\(a\), вкажіть його. Якщо ні, обговоріть, чому немає меж
\(f(x)=\begin{cases} \frac{1}{x}−3, && \text{if }x≤2 \\ x^3+1, && \text{if } x>2 \end{cases} a=2\)
\(\lim \limits_{x \to 2^−} f(x)=−\frac{5}{2}a\)І\(\lim \limits_{x \to 2^+} f(x)=9\) Таким чином, межі функції як\(x\) наближається 2 не існує.
\(f(x)=\begin{cases} x^3+1, && \text{if }x<1 \\ 3x^2−1, && \text{if } x=1 \\ −\sqrt{x+3}+4, && \text{if } x>1 \end{cases} a=1\)
Для наступних вправ оцініть кожну межу за допомогою алгебраїчних прийомів.
\(\lim \limits_{x \to −5}(\frac{\frac{1}{5}+\frac{1}{x}}{10+2x})\)
\(−\frac{1}{50}\)
\(\lim \limits_{h \to 0} (\frac{\sqrt{h^2+25}−5}{h^2})\)
\(\lim \limits_{h \to 0} (\frac{1}{h}−\frac{1}{h^2+h})\)
1
Для наступних вправ визначте, чи є дана функція\(f\) безперервною чи ні. Якщо він безперервний, покажіть чому. Якщо він не є безперервним, станьте, які умови не вдаються.
\(f(x)=\sqrt{x^2−4}\)
\(f(x)=\frac{x^3−4x^2−9x+36}{x^3−3x^2+2x−6}\)
знімний розрив при\(x=3\)
Для наступних вправ використовуйте визначення похідної, щоб знайти похідну заданої функції при\(x=a\).
\(f(x)=\frac{3}{5+2x}\)
\(f(x)=\frac{3}{\sqrt{x}}\)
\(f'(x)=−\frac{3}{2a^{\frac{3}{2}}}\)
\(f(x)=2x^2+9x\)
переривчастий при —2,0, не диференційований при —2,0, 2.
Для наступних вправ за допомогою графічної утиліти поясніть, чому функція не диференційована скрізь у своїй області. Вкажіть точки, де функція не диференційована.
\(f(x)=| x−2 |−| x+2 |\)
\(f(x)=\frac{2}{1+e^{\frac{2}{x}}}\)
не диференційований на\(x=0\) (без обмежень)
Для наступних вправ поясніть позначення словами, коли висота снаряда в ногах\(s\), є функцією часу t t в секундах після запуску і задається функцією\(s(t)\).
\(s(0)\)
\(s(2)\)
висота снаряда в\(t=2\) секундах
\(s'(2)\)
\(\frac{s(2)−s(1)}{2−1}\)
середня швидкість від\(t=1\) до\(t=2\)
\(s(t)=0\)
Для наступних вправ використовуйте технологію оцінки межі.
\(\lim \limits_{x \to 0} \frac{\sin (x)}{3x}\)
\(\frac{1}{3}\)
\(\lim \limits_{x \to 0} \frac{\tan ^2 (x)}{2x}\)
\(\lim \limits_{x \to 0}\frac{\sin (x)(1−\cos (x))}{2x^2}\)
0
Оцініть ліміт вручну.
\(\lim \limits_{x \to 1}f(x), \text{where } f(x)= \begin{cases} 4x−7 && x≠1 \\ x^2−4 &&x=1 \end{cases}\)
При якому значенні (s)\(x\) є функція нижче розривної?
\(f(x)= \begin{cases} 4x−7 && x≠1 \\ x^2−4 &&x=1 \end{cases}\)
Для наступних вправ розглянемо функцію, графік якої відображається на малюнку.
Знайти середню швидкість зміни функції від\(x=1\) до\(x=3\).
2
Знайти всі значення\(x\) при якому\(f'(x)=0\).
\(x=1\)
Знайти всі значення\(x\) при яких\(f'(x)\) не існує.
Знайдіть рівняння дотичної прямої до графіка\(f\) зазначеної точки:\(f(x)=3x^2−2x−6, x=−2\)
\(y=−14x−18\)
Для наступних вправ використовуйте функцію\(f(x)=x(1−x)^{\frac{2}{5}}\).
Графік функції\(f(x)=x(1−x)^{\frac{2}{5}}\) шляхом введення,\(f(x)=x((1−x)^2)^{\frac{1}{5}}\) а потім шляхом введення\(f(x)=x((1−x)^{\frac{1}{5}})^2\).
Дослідіть поведінку графіка\(f(x)\) навколо,\(x=1\) намалювавши функцію на наступних областях, [0.9, 1.1], [0.99, 1.01], [0.999, 1.001] та [0.9999, 1.0001]. Використовуйте цю інформацію, щоб визначити, чи видається функція диференційованою на\(x=1\).
Графік не диференційовний на\(x=1\) (cusp).
Для наступних вправ знайдіть похідну кожної з функцій за допомогою визначення:\(\lim \limits_{h \to 0} \frac{f(x+h)−f(x)}{h}\)
\(f(x)=2x−8\)
\(f(x)=4x^2−7\)
\(f′(x)=8x\)
\(f(x)=x−\frac{1}{2}x^2\)
\(f(x)=\frac{1}{x+2}\)
\(f'(x)=−\frac{1}{(2+x)^2}\)
\(f(x)=\frac{3}{x−1}\)
\(f(x)=−x^3+1\)
\(f′(x)=−3^x2\)
\(f(x)=x^2+x^3\)
\(f(x)=\sqrt{x−1}\)
\(f'(x)=\frac{1}{2\sqrt{x−1}}\)
Виноски
- 1 www.csun.edu/наука/здоров'я/д... tv&health.html Джерело надано.
Глосарій
- середня швидкість зміни
- нахил лінії, що з'єднує дві точки\((a,f(a))\) і\((a+h,f(a+h))\) на кривій\(f(x)\); він задається
\[\text{AROC}=\dfrac{f(a+h)−f(a)}{h}.\]
- похідний
- нахил функції в заданій точці; позначається\(f′(a)\), в точці\(x=a\) вона є\(f′(a)=\lim \limits_{h \to 0}\frac{f(a+h)−f(a)}{h}\), за умови, що межа існує.
- диференційований
- функція,\(f(x)\) для якої похідна існує\(x=a.\) в Іншими словами, якщо існує f′ (a) f′ (a) f′ (a).
- миттєва швидкість зміни
- нахил функції в заданій точці; в\(x=a\) ньому задається\(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}\).
- миттєва швидкість
- зміна швидкості або напрямку в даний момент; функція\(s(t)\) представляє положення об'єкта в той час\(t\), а миттєва швидкість або швидкість об'єкта в час\(t=a\) задається\(s′(a)=\lim \limits_{h \to 0}\frac{s(a+h)−s(a)}{h}\).
- січна лінія
- лінія, яка перетинає дві точки на кривій
- дотична лінія
- лінія, яка перетинає криву в одній точці
