12.3: Безперервність

Арізона відома своєю сухою спекою. У певний день температура може піднятися настільки ж високо, як\(118^∘F\) і опуститися лише до жвавого\(95^∘F.\) Рисунок\(\PageIndex{1}\) показує функцію\(T\), де на виході\(T(x)\) є температура в градусах Фаренгейта, а вхід\(x\) - це час доби, використовуючи цілодобовий годинник на особливий літній день.

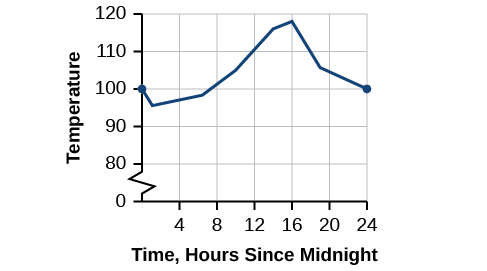
Малюнок\(\PageIndex{1}\): Температура як функція часу утворює безперервну функцію.

Коли ми аналізуємо цей графік, ми помічаємо конкретну характеристику. У графіку немає перерв. Ми могли простежити графік, не взявши в руки наш олівець. Це єдине спостереження говорить нам багато про функцію. У цьому розділі ми будемо досліджувати функції з перервами і без них.

Визначення того, чи є функція безперервною за числом

Розглянемо конкретний приклад температури з точки зору дати і місця розташування, такий як 27 червня 2013 року в Феніксі, штат Арізона. Графік на малюнку\(\PageIndex{1}\) вказує на те, що о 2 годині ранку температура була\(96 ^∘F\). До 14:00 температура піднялася\(116^∘F,\) і до 4 вечора це було\(118 ^∘F.\) десь між 2 ранку і 16:00 температура зовні, мабуть, була точно\(110.5 ^∘ F\). Насправді будь-яка температура між\(96 ^∘ F\) і\(118 ^∘ F\) виникла в якийсь момент того дня. Це означає, що всі дійсні числа на виході між\(96 ^∘ F\) і\(118 ^∘ F\) генеруються в якийсь момент функцією відповідно до теореми проміжного значення,

Подивіться ще раз на Малюнок\(\PageIndex{1}\). У графіку функції для цього 24-годинного періоду немає перерв. Ні в якому разі температура не перестала існувати, а також не було точки, в якій температура миттєво підскочила на кілька градусів. Функція, яка не має дірок або розривів у своєму графіку, відома як безперервна функція. Температура як функція часу є прикладом безперервної функції.

Якщо температура являє собою безперервну функцію, яка функція не була б безперервною? Розглянемо приклад доларів, виражених як функція годин паркування. Давайте створимо функцію\(D\), де\(D(x)\) є висновок, що представляє вартість в доларах за\(x\) кількість годин паркування (рис.\(\PageIndex{2}\)).

Припустимо, паркувальний гараж стягує 4,00 доларів на годину або частку години, з максимальною зарядкою 25 доларів на день. Паркуйтеся на дві години і п'ять хвилин, а плата становить 12 доларів. Паркуйте додаткову годину і плата становить 16 доларів. Ми ніколи не можемо стягувати $13, $14 або $15. Існують дійсні числа між 12 і 16, які функція ніколи не виводить. У графіку функції за цей 24-годинний період є перерви, бали, при яких ціна паркування миттєво скаче на кілька доларів.

Малюнок\(\PageIndex{2}\): Паркувально-гаражні збори утворюють переривчасту функцію.

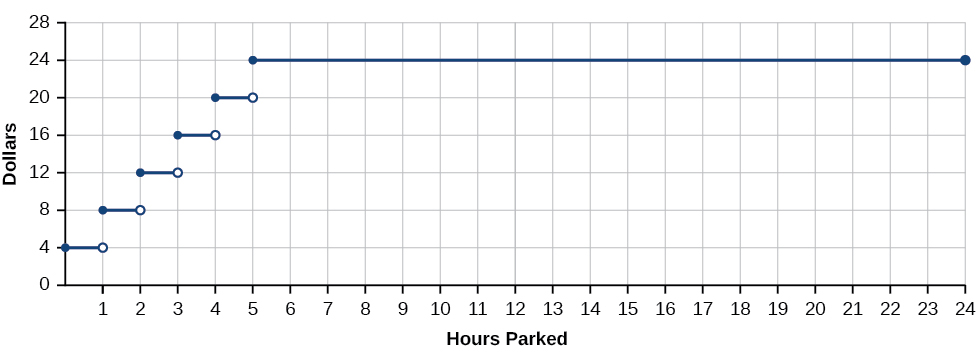
Функція, яка залишається рівнем для інтервалу, а потім миттєво переходить до більш високого значення, називається ступеневою функцією. Ця функція є прикладом.

Функція, яка має будь-яку дірку або розрив у своєму графіку, відома як переривчаста функція. Ступінчаста функція, така як паркувально-гаражні збори як функція годин, припаркованих, є прикладом переривчастої функції.

Так як ми можемо вирішити, якщо функція безперервна на певне число? Ми можемо перевірити три різні умови. Давайте використаємо функцію,\(y=f(x)\) представлену на малюнку як приклад.

Малюнок_12_03_004">Рисунок.

Рисунок_12_03_003">Фігура наближається\(x=a\) зліва і справа, наближається та ж y -координата. Тому умова 2 виконується. Однак у графіку все ще може бути діра на\(x=a\).

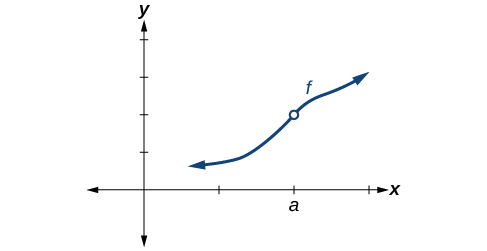
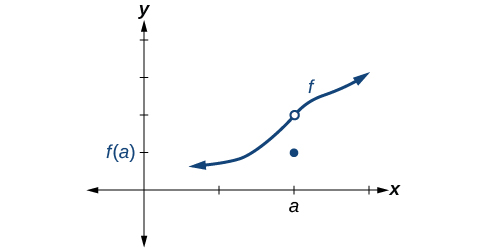
Умова 3 Відповідно до Умови 3, відповідна координата y y при\(x=a\) заповнює дірку на графіку\(f\). Про це написано\(\lim \limits_{x \to a} f(x)=f(a)\).

Задоволення всіх трьох умов означає, що функція безперервна. Усі три умови виконуються для функції, представленої на рисунку, тому функція є безперервною як\(x=a\).

Всі три умови виконані. Функція безперервна при\(x=a\).

Рисунок через рисунок наведено кілька прикладів графіків функцій, які не є безперервними в\(x=a\) і умови або умови, які не працюють.

Умова 2 виконано. Умови 1 і 3 обидва виходять з ладу.

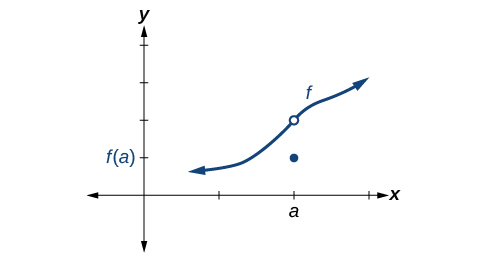
Умови 1 і 2 виконуються обидва. Умова 3 не вдається.

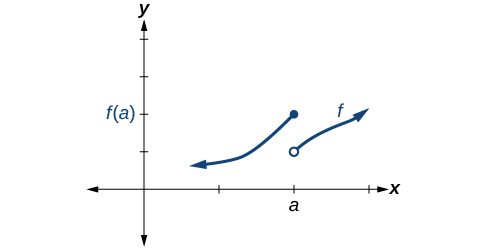
Умова 1 виконано. Умови 2 і 3 виходять з ладу.

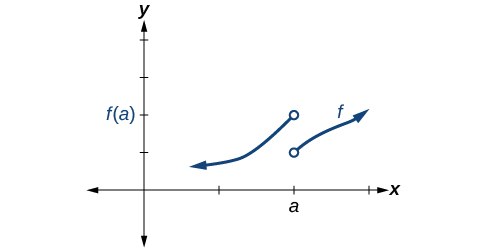
Умови 1, 2 і 3 все не вдається.

Визначення безперервності

Функція\(f(x)\) є безперервною за\(x=a\) умови виконання всіх трьох наступних умов:

• Умова 1:\(f(a)\) існує.
• Умова 2:\(\lim \limits_{x \to a} f(x)\) існує в\(x=a\).
• Умова 3:\(\lim \limits_{x \to a} f(x)=f(a)\)

Якщо функція не\(f(x)\) є безперервною в\(x=a\), функція переривається в\(x=a\).

Визначення розриву стрибка

Розрив може відбуватися по-різному. Ми бачили в попередньому розділі, що функція може мати ліву межу і праву межу, навіть якщо вони не рівні. Якщо ліві та праві межі існують, але різні, графік «стрибає» на\(x=a\). Кажуть, що функція має стрибок розриву.

Як приклад розглянемо графік функції на\(y=f(x)\) малюнку. Зверніть увагу,\(a\) як\(x\) підходить, як вихід наближається до різних значень зліва і справа.

Графік функції з розривом стрибка.

РОЗРИВ СТРИБКА

Функція\(f(x)\) має стрибок розриву,\(x=a\) якщо ліві та праві межі існують, але не рівні:\( \lim \limits_{x \to a^−} f(x)≠ \lim \limits_{x \to a^+} f(x)\)

Визначення знімних розривів

Деякі функції мають розрив, але в цей момент можна перевизначити функцію, щоб зробити її безперервною. Цей тип функції, як кажуть, має знімний розрив. Давайте розглянемо функцію,\(y=f(x)\) представлену графіком на малюнку. Функція має обмеження. Однак є дірка при\(x=a\). Дірку можна заповнити шляхом розширення області для включення вхідних даних\(x=a\) і визначення відповідного виходу функції при цьому значенні як межа функції at\(x=a\).

Графік функції\(f\) зі знімним розривом в\(x=a\).

знімний розрив

Функція f (x) f (x) має знімний розрив,\(x=a\) якщо межа\(\lim \limits_{x \to a} f(x),\) існує, але або

1. \(f(a)\)не існує або
2. \(f(a)\), Значення функції при\(x=a\) не дорівнює межі,\(f(a)≠ \lim \limits_{x \to a} f(x)\).

Приклад\(\PageIndex{1}\): Identifying Discontinuities

Визначте всі розриви для наступних функцій як стрибок або знімний розрив.

1. \(f(x)=\frac{x^2−2x−15}{x−5}\)
2. \[ g(x)= \begin{cases} x+1, & x<2 \\ −x, & x≥2 \end{cases} \]

1. Зверніть увагу, що функція визначається скрізь, крім at\(x=5\).

   Таким чином,\(f(5)\) не існує, умова 2 не виконується. Оскільки умова 1 виконується, межа при\(x\) наближенні 5 дорівнює 8, а умова 2 не задовольняється.Це означає, що є знімний розрив при\(x=5\).

2. Умова 2 виконана, тому що\(g(2)=−2.\)

   Зверніть увагу, що функція є кусковою функцією, і для кожного фрагмента функція визначається скрізь у своїй області. Розглянемо Умова 1, визначивши ліву і праву межі як\(x\) підходи 2.

   Ліва межа:\(\lim \limits_{x \to 2^−} (x+1)=2+1=3\). Ліва межа існує.

   Правостороння межа:\(\lim \limits_{x \to 2^+} (−x)=−2\). Правий ліміт існує. Але

   \[\lim \limits_{x \to 2^−} f(x)≠ \lim \limits_{x \to 2^+} f(x).\]

   Отже,\(\lim \limits_{x \to 2} f(x)\) не існує, і умова 2 виходить з ладу: немає знімного розриву. Однак, оскільки ліві та праві межі існують, але не рівні, умови розриву стрибка виконуються при\(x=2\).

Вправа\(\PageIndex{1}\):

Визначте всі розриви для наступних функцій як стрибок або знімний розрив.

1. \(f(x)=\frac{x^2−6x}{x−6}\)
2. \(g(x)= \begin{cases} \sqrt{x}, & 0≤x<4 \\ 2x, & x≥4 \end{cases} \)

1. знімний розрив при\(x=6\);
2. стрибок розриву при\(x=4\)

Розпізнавання безперервних та переривчастих функцій реального числа

Багато функцій, з якими ми стикалися в попередніх розділах, є безперервними всюди. У них ніколи не буває дірки, і вони ніколи не перестрибують з одного значення на інше. Для всіх цих функцій\(f(x)\) межа as\(x\) наближається до a така ж, як і значення\(f(x)\) коли\(x=a\). Отже\(\lim \limits_{x \to a} f(x)=f(a)\). Є деякі функції, які є безперервними скрізь, а деякі, які є лише безперервними, де вони визначені на їхньому домені, оскільки вони не визначені для всіх дійсних чисел.

ПРИКЛАДИ НЕПЕРЕРВНИХ ФУНКЦІЙ

Наступні функції є безперервними всюди:

Поліноміальні функції	Ex:\(f(x)=x^4−9x^2\)
Експоненціальні функції	Ex:\(f(x)=4^{x+2}−5\)
Функції синуса	Ex:\(f(x)=\sin (2x)−4\)
Функції косинуса	Ex:\(f(x)=− \cos (x+\frac{π}{3})\)

Наступні функції є безперервними скрізь, де вони визначені на їх області:

Логарифмічні функції	Ex:\(f(x)=2 \ln (x), x>0\)
Функції дотичної	Ex:\(f(x)= \tan (x)+2, x≠ \frac{π}{2}+kπ, k\) є цілим числом
раціональні функції	Ex:\(f(x)=\frac{x^2−25}{x−7}, x≠7\)

how to:задано функцію\(f(x)\), determine if the function is continuous at \(x=a\).

1. Перевірте Умова 1:\(f(a)\) існує.
2. Перевірте Умова 2:\(\lim \limits_{x \to a} f(x)\) існує в\(x=a\).
3. Перевірити умову 3:\(\lim \limits_{x \to a} f(x)=f(a).\)
4. Якщо всі три умови виконані, функція безперервна при\(x=a\). Якщо якась одна з умов не виконується, функція не є безперервною при\(x=a\).

Приклад\(\PageIndex{2}\): Determining Whether a Piecewise Function is Continuous at a Given Number

Визначте, чи\(f(x)= \begin{cases} 4x, & x≤3 \\ 8+x, & x>3 \end{cases}\) є функція безперервною при

1. \(x=3\)
2. \(x=\frac{8}{3}\)

Щоб визначити, чи\(f\) є функція безперервною,\(x=a,\) ми визначимо, чи задовольняються три умови безперервності в\(x=a\).

1. Умова 1: Чи\(f(a)\) існує?

   \[\begin{align} f(3)=4(3)=12 \\ ⇒ \text{Condition 1 is satisfied.} \end{align} \]

   Умова 2: Чи\(\lim \limits_{x \to 3} f(x)\) існує?

   Зліва\(x=3, f(x)=4x;\) праворуч від\(x=3, f(x)=8+x.\) Ми повинні оцінити ліву і праву межі як\(x\) підходи 1.

   • Ліва межа:\(\lim \limits_{x \to 3^−} f(x)= \lim \limits_{x \to 3^−} 4(3)=12\)
   • Правостороння межа:\(\lim \limits_{x \to 3^+} f(x)= \lim \limits_{x \to 3^+}(8+x)=8+3=11\)

   Тому що\(\lim \limits_{x \to 1^−} f(x)≠ \lim \limits_{x \to 1^+} f(x), \lim \limits_{x \to 1} f(x)\) не існує.

   \[⇒ \text{Condition 2 fails.}\]

   Далі йти не потрібно. Умова 2 не вдається при\(x=3\). Якщо будь-яка з умов безперервності не задовольняється при\(x=3\), функція не\(f(x)\) є безперервною при\(x=3\).

2. \(x=\frac{8}{3}\)

   Умова 1: Чи\(f(\frac{8}{3})\) існує?

   \[\begin{align} f(\frac{8}{3})=4(\frac{8}{3})=\frac{32}{3} \\ ⇒\text{Condition 1 is satisfied.} \end{align}\]

   Умова 2: Чи\(\lim \limits_{x \to \frac{8}{3}} f(x)\) існує?

   Зліва від\(x=\frac{8}{3}\),\(f(x)=4x\); праворуч від\(x=\frac{8}{3}, f(x)=8+x\). Нам потрібно оцінювати ліву та праву межі як\(x\) підходи\(\frac{8}{3}\).

   • Ліва межа:\(\lim \limits_{x \to \frac{8}{3}^−} f(x)= \lim \limits_{x \to \frac{8}{3}^−} 4(\frac{8}{3})=\frac{32}{3}\)
   • Правостороння межа:\(\lim \limits_{x \to \frac{8}{3}^+} f(x)= \lim \limits_{x \to \frac{8}{3}^+} (8+x)=8+\frac{8}{3}=\frac{32}{3}\)

   Тому що\(\lim \limits_{x \to \frac{8}{3}} f(x)\) існує,

   \[⇒ \text{Condition 2 is satisfied.}\]

   Умова 3: Чи є\(f(\frac{8}{3})=\lim \limits_{x \to \frac{8}{3}} f(x)\)?

   \[\begin{align} f(\frac{32}{3})=\frac{32}{3}=\lim \limits_{x \to \frac{8}{3}} f(x) \\ ⇒ \text{Condition 3 is satisfied.} \end{align}\]

   Оскільки всі три умови безперервності задовольняються на\(x=\frac{8}{3}\), функція\(f(x)\) є безперервною в\(x=\frac{8}{3}\).

Вправа\(\PageIndex{2}\):

Визначте, чи\(f(x)= \begin{cases} & \frac{1}{x}, && x≤2 \\ & 9x−11.5, && x>2 \end{cases}\) є функція безперервною в\(x=2\).

так

Приклад\(\PageIndex{3}\): Determining Whether a Rational Function is Continuous at a Given Number

Визначте, чи\(f(x)=\frac{x^2−25}{x−5}\) є функція безперервною в\(x=5\).

Щоб визначити, чи\(f\) є функція безперервною в\(x=5\), ми визначимо, чи задовольняються три умови безперервності при\(x=5\).

Стан 1:

\[\begin{align} f(5) \text{ does not exist.} \\ ⇒ \text{Condition 1 fails.} \end{align}\]

Далі йти не потрібно. Умова 2 не вдається при\(x=5\). Якщо будь-яка з умов безперервності не задовольняється at\(x=5\), функція f f не є безперервною at\(x=5\).

Аналіз

Див. Малюнок. Зверніть увагу, що для умови 2 ми маємо

\[\begin{align} \lim \limits_{x \to 5} \dfrac{x^2−25}{x−5} &= \lim \limits_{x \to 3} \dfrac{\cancel{(x−5)}(x+5)}{\cancel{x−5}} \\ &= \lim \limits_{x \to 5}(x+5) \\ &=5+5=10 \\ &⇒ \text{Condition 2 is satisfied.} \end{align}\]

При x=5, x=5 існує знімний розрив. Див. Малюнок.

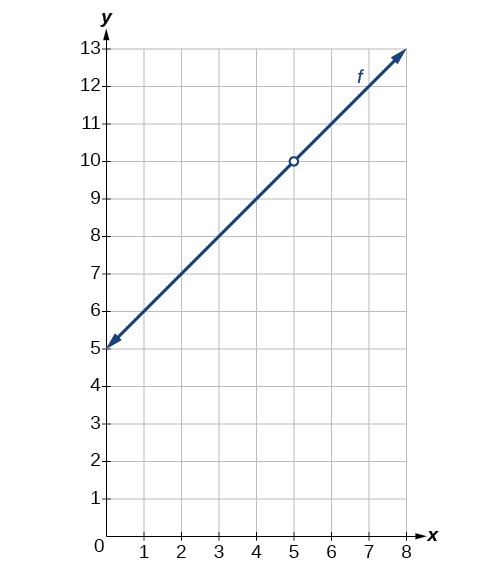
Вправа\(\PageIndex{3}\):

Визначте, чи\(f(x)=\frac{9−x^2}{x^2−3x}\) є функція безперервною в\(x=3\). Якщо ні, вкажіть тип розриву.

Ні, функція не є безперервною в\(x=3\). Існує знімний розрив при\(x=3\).

Визначення вхідних значень, для яких функція є переривчастою

Тепер, коли ми можемо визначити безперервні функції, розриви стрибків та знімні розриви, ми розглянемо більш складні функції, щоб знайти розриви. Тут ми проаналізуємо кускову функцію, щоб визначити, чи існують будь-які дійсні числа, де функція не є безперервною. Кусково функція може мати розриви в граничних точках функції, а також всередині функцій, які її складають.

Для визначення дійсних чисел, для яких кускова функція, складена з поліноміальних функцій, не є безперервною, нагадаємо, що самі поліноміальні функції є неперервними на множині дійсних чисел. Будь-який розрив буде в граничних точках. Отже, нам потрібно дослідити три умови неперервності в граничних точках кускової функції.

how to: За допомогою кускової функції визначити, чи є вона безперервною в граничних точках

1. Для кожної\(a\) граничної точки кускової функції визначте ліву та праву межі\(a, \) як\(x\) підходи, так і значення функції в\(a\).
2. Перевірте кожну умову для кожного значення, щоб визначити, чи всі три умови виконані.
3. Визначте, чи задовольняє кожне значення умові 1:\(f(a)\) існує.
4. Визначте, чи задовольняє кожне значення умові 2:\(\lim \limits_{x \to a} f(x)\) існує.
5. Визначте, чи задовольняє кожне значення умові 3:\(\lim \limits_{x \to a} f(x)=f(a).\)
6. Якщо всі три умови виконані, функція безперервна при\(x=a\). Якщо будь-яка з умов не виходить з ладу, функція не є безперервною при\(x=a\).

Приклад\(\PageIndex{4}\): Determining the Input Values for Which a Piecewise Function Is Discontinuous

Визначте, чи є функція f переривчастою для будь-яких дійсних чисел.

\[fx= \begin{cases} x+1, &x<2 \\ 3, &2≤x<4 \\ x^2−11, & x≥4 \end{cases} \]

Аналіз

Див. Малюнок. При\(x=4\), існує стрибок розриву. Зверніть увагу, що функція безперервна на\(x=2\).

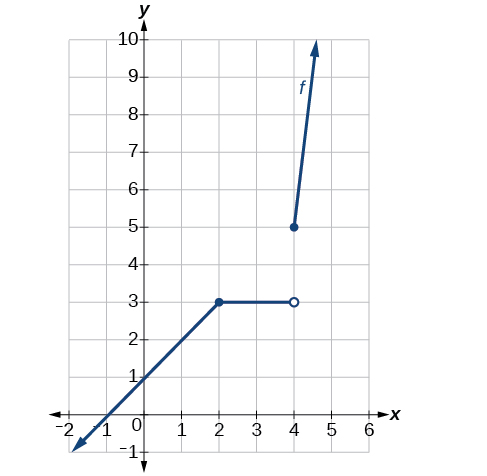
Графік є безперервним при\(x=2\) but shows a jump discontinuity at \(x=4\).

Вправа\(\PageIndex{4}\):

Визначте, де функція\(f(x)= \begin{cases} \frac{πx}{4}, &x<2 \\ \frac{π}{x}, & 2≤x≤6 \\ 2πx, &x>6 \end{cases}\) переривається.

\(x=6\)

Визначення того, чи є функція безперервною

Щоб визначити, чи є кускова функція безперервною чи переривчастою, крім перевірки граничних точок, ми також повинні перевірити, чи є кожна з функцій, що складають кускову функцію, безперервною.

як: З огляду на кускову функцію, визначити, чи є вона безперервною.

1. Визначте, чи є кожна компонентна функція кускової функції безперервною. Якщо є розриви, чи відбуваються вони в області, де застосовується ця функція компонента?
2. Для кожної\(x=a\) граничної точки кускової функції визначте, чи дотримується кожна з трьох умов.

Приклад\(\PageIndex{5}\): Determining Whether a Piecewise Function Is Continuous

Визначте, чи функція нижче безперервна. Якщо це не так, вкажіть місце і тип кожного розриву.

\[fx= \begin{cases} \sin (x), &x<0 \\ x^3, & x>0 \end{cases}\]

Дві функції, що складають цю кускову функцію, увімкнені\(x<0\) та\(f(x)=\sin (x)\)\(f(x)=x^3\) ввімкнені\(x>0\). Функція синуса і всі поліноміальні функції є безперервними всюди. Будь-які розриви були б у граничній точці,

На\(x=0\), давайте перевіримо три умови безперервності.

Стан 1:

\[ \begin{align} f(0) \text{ does not exist.} \\ ⇒ \text{Condition 1 fails.} \end{align}\]

Оскільки всі три умови не задовольняються на\(x=0\), функція\(f(x)\) переривається на\(x=0\).

Аналіз

Див. Малюнок. Існує знімний розрив при\(x=0\);\(\lim \limits_{x \to 0} f(x)=0\), Таким чином межа існує і є кінцевою, але\(f(a)\) не існує.

Функція має знімний розрив при 0.

Медіа

Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з безперервністю.

• Безперервність у точці
• Безперервність у точці: перевірка концепції

Ключові концепції

• Неперервна функція може бути представлена графіком без дірок або розривів.
• Функція, графік якої має дірки, є переривчастою функцією.
• Функція є безперервною за певним числом, якщо виконуються три умови:
  • Умова 1:\(f(a)\) існує.
  • Умова 2:\(\lim \limits_{x \to a} f(x)\) існує в\(x=a\).
  • Умова 3:\(\lim \limits_{x \to a} f(x)=f(a)\).
• Функція має стрибок розриву, якщо ліві та праві межі різні, що призводить до того, що графік «стрибатиме».
• Функція має знімний розрив, якщо її можна перевизначити в переривчастої точці, щоб зробити її безперервною. Див. Приклад.
• Деякі функції, такі як поліноміальні функції, скрізь безперервні. Інші функції, такі як логарифмічні функції, є неперервними у своїй області. Див. Приклад і Приклад.
• Щоб кускова функція була безперервною, кожен шматок повинен бути безперервним на своїй частині області, а функція в цілому повинна бути безперервною на кордоні. Див. Приклад і Приклад.

Глосарій

безперервна функція

функція, яка не має отворів або розривів у своєму графіку

переривчаста функція

функція, яка не є безперервною\(x=a\)

стрибок розриву

точка розриву\(f(x)\) у функції,\(x=a\) де існують і ліва, і права межі, але\(\lim \limits_{x \to a^−} f(x)≠ \lim \limits_{x \to a^+} f(x)\)

знімний розрив

точка розриву у функції,\(f(x)\) де функція є переривчастою, але може бути перевизначена, щоб зробити її безперервною