5.1: Десяткові знаки (частина 1)
- Page ID
- 57904
- Назва десяткових знаків
- Запишіть десяткові знаки
- Перетворення десяткових дробів на дроби або мішані числа
- Знайдіть десяткові знаки на числовому рядку
- Порядок десяткових знаків
- Круглі десяткові знаки
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Назвіть число 4 926 015 прописом. Якщо ви пропустили цю проблему, перегляньте приклад 1.1.4.
- Раунд 748 до найближчої десяти. Якщо ви пропустили цю проблему, перегляньте приклад 1.2.9.
- Знайдіть\(\dfrac{3}{10}\) на числовому рядку. Якщо ви пропустили цю проблему, перегляньте приклад 4.2.16.
Назва десяткових знаків
Ви, напевно, вже знаєте зовсім небагато про десяткові знаки на основі вашого досвіду роботи з грошима. Припустимо, ви купуєте бутерброд і пляшку води на обід. Якщо сендвіч коштує 3,45 долара, пляшка води коштує 1,25 долара, а загальний податок з продажу - 0,33 долара, яка загальна вартість вашого обіду?
\[\begin{split} & $3.45 \qquad Sandwich \\ & $1.25 \qquad Water \\ + & $0.33 \qquad Tax \\ \hline & $5.03 \qquad Total \end{split}\]
Загальна сума становить $5.03. Припустимо, ви платите з рахунком у 5 доларів та 3 копійки. Чи варто чекати змін? Ні, 5 доларів і 3 копійки - це те ж саме, що $5.03.
Оскільки 100 копійок = 1 долар, кожна копійка коштує\(\dfrac{1}{100}\) долар. Значення однієї копійки записуємо як $0,01, так як 0,01 =\(\dfrac{1}{100}\).
Написання числа з десятковим числом відоме як десяткове позначення. Це спосіб показати частини цілого, коли ціле - це сила десяти. Іншими словами, десяткові числа - ще один спосіб запису дробів, знаменниками яких є повноваження десяти. Подібно до того, як підрахункові числа засновані на степенях десяти, десяткові числа базуються на степенях десяти. Таблиця\(\PageIndex{1}\) показує підрахунок чисел.
| Кількість підрахунку | Ім'я |
|---|---|
| 1 | Один |
| 10 = 10 | Десятка |
| 10 • 10 = 100 | Сто |
| 10 • 10 • 10 = 1000 | Тисяча |
| 10 • 10 • 10 • 10 = 10 000 | Десять тисяч |
Як десяткові числа пов'язані з дробами? Таблиця\(\PageIndex{2}\) показує відношення.
| Десяткова | Дріб | Ім'я |
|---|---|---|
| 0.1 | \(\dfrac{1}{10}\) | Одна десята |
| 0,01 | \(\dfrac{1}{100}\) | Сотий |
| 0,001 | \(\dfrac{1}{1000}\) | Тисячна |
| 0,0001 | \(\dfrac{1}{10,000}\) | Один десятитисячний |
Коли ми називаємо ціле число, ім'я відповідає значенню місця на основі степеней десяти. У Цілих числах ми навчилися читати 10 000 як десять тисяч. Аналогічним чином імена десяткових знаків відповідають їх значенням дробу. Зверніть увагу, як назви топонімів на малюнку\(\PageIndex{1}\) співвідносяться з назвами дробів з таблиці\(\PageIndex{2}\).
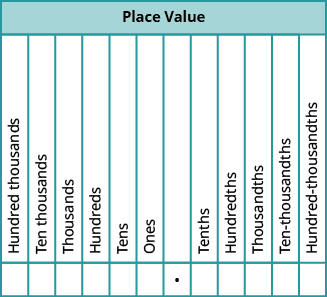
Малюнок\(\PageIndex{1}\) - Ця діаграма ілюструє значення місця ліворуч і праворуч від десяткової крапки.
Зверніть увагу на два важливих факту, показаних на малюнку\(\PageIndex{1}\).
- Значення «й» в кінці імені означає, що число - дріб. «Тисяча» - це число більше одиниці, але «тисячна» - це число менше одиниці.
- Десяте місце - це перше місце праворуч від десяткового рядка, але десяте місце - два розряди зліва від десяткової.
Пам'ятайте, що $5,03 обід? Ми читаємо $5.03 як п'ять доларів і три центи. Назви десяткових знаків (тих, які не представляють гроші) робиться аналогічним чином. Число 5.03 читаємо як п'ять і три соті.
Іноді нам потрібно перевести число, записане в десяткових числах, в слова. Як показано на малюнку\(\PageIndex{2}\), записуємо суму на чеку як словами, так і цифрами.

Малюнок\(\PageIndex{2}\) - Коли ми пишемо чек, ми записуємо суму як десятковим числом, так і прописом. Банк дивиться на чек, щоб переконатися, що обидва числа збігаються. Це допомагає запобігти помилкам.
| Спробуємо назвати десяткове число, наприклад 15.68. | |
| Почнемо з іменування числа зліва від десяткового. | п'ятнадцять______ |
| Використовуємо слово «і» для позначення десяткової крапки. | п'ятнадцять і_____ |
| Тоді ми називаємо число праворуч від десяткової крапки, як якщо б це було ціле число. | п'ятнадцять і шістдесят вісім_____ |
| Прізвище, назвіть десятковий розряд останньої цифри. | п'ятнадцять і шістдесят вісім сотих |
Число 15,68 читається п'ятнадцять і шістдесят вісім сотих.
- Назвіть число ліворуч від десяткової крапки.
- Запишіть «і» для десяткової крапки.
- Назвіть частину «число» праворуч від десяткової крапки так, ніби це ціле число.
- Назвіть десятковий розряд останньої цифри.
Назвіть кожне десяткове число: (a) 4.3 (b) 2.45 (c) 0.009 (d) −15.571.
Рішення
(а) 4.3
| Назвіть число ліворуч від десяткової крапки. | чотири _____ |
| Запишіть «і» для десяткової крапки. | чотири і_____ |
| Назвіть число праворуч від десяткової крапки так, ніби це ціле число. | чотири і три_____ |
| Назвіть десятковий розряд останньої цифри. | чотири і три десяті |
(б) 2,45
| Назвіть число ліворуч від десяткової крапки. | два-_____ |
| Запишіть «і» для десяткової крапки. | два і_____ |
| Назвіть число праворуч від десяткової крапки так, ніби це ціле число. | два і сорок п'ять_____ |
| Назвіть десятковий розряд останньої цифри. | дві і сорок п'ять сотих |
(с) 0,009
| Назвіть число ліворуч від десяткової крапки. | Нуль - це число ліворуч від десяткового числа; воно не включається в ім'я. |
| Назвіть число праворуч від десяткової крапки так, ніби це ціле число. | дев'ять_____ |
| Назвіть десятковий розряд останньої цифри. | дев'ять тисячних |
(д) −15,571
| Назвіть число ліворуч від десяткової крапки. | негативні п'ятнадцять |
| Запишіть «і» для десяткової крапки. | негативні п'ятнадцять і_____ |
| Назвіть число праворуч від десяткової крапки так, ніби це ціле число. | негативні п'ятнадцять п'ятсот сімдесят один_____ |
| Назвіть десятковий розряд останньої цифри. | негативні п'ятнадцять і п'ятсот сімдесят тисячних |
Назва кожного десяткового числа: (a) 6.7 (b) 19.58 (c) 0,018 (d) −2.053
- Відповідь на
-
шість і сім десятих
- Відповідь б
-
дев'ятнадцять і п'ятдесят вісім сотих
- Відповідь c
-
вісімнадцять тисячних
- Відповідь d
-
негативні дво- і пятьдесят тритисячні
Назва кожної десяткової коми: (a) 5.8 (b) 3.57 (c) 0,005 (d) −13,461
- Відповідь на
-
п'ять і вісім десятих три і п'ятдесят сім сотих
- Відповідь б
-
три і п'ятдесят сім сотих
- Відповідь c
-
п'ять тисячних
- Відповідь d
-
негативні тринадцять і чотириста шестьдесят одна тисячна
Напишіть десяткові знаки
Тепер ми переведемо ім'я десяткового числа в десяткові позначення. Ми скасуємо процедуру, яку ми тільки що використовували. Почнемо з написання числа шість і сімнадцять сотих:
| Слово і говорить нам поставити десяткову крапку. | ___ . ___ |
| Слово перед і є цілим числом; запишіть його зліва від десяткової крапки. | 6. _____ |
| Десяткова частина - сімнадцять сотих. Відзначте два місця праворуч від десяткової крапки для сотих. | 6._ _ |
| Напишіть цифри для сімнадцяти в зазначених місцях. | 6.17 |
Запишіть чотирнадцять і тридцять сім сотих як десяткове число.
Рішення
| Поставте десяткову крапку під словом «і'. | ______ . _________ |
| Перекладіть слова перед «і» в ціле число і помістіть його ліворуч від десяткової крапки. | 14. _________ |
| Відзначте два місця праворуч від десяткової крапки для «сотих». | 14.__ __ |
| Переведіть слова після «і» і напишіть число праворуч від десяткової крапки. | 14.37 |
Чотирнадцять і тридцять сім сотих написано 14.37.
Пишіть як десяткове число: тринадцять і шістдесят вісім сотих.
- Відповідь
-
13.68
Запишіть як десяткове число: п'ять і вісімсот дев'яносто чотири тисячні.
- Відповідь
-
5.894
Крок 1. Шукайте слово «і» —воно знаходить десяткову крапку.
Крок 2. Відзначте потрібну кількість десяткових знаків праворуч від десяткової крапки, зазначивши значення місця, зазначене останнім словом.
- Поставте десяткову крапку під словом «і». Переведіть слова перед «і» в ціле число і помістіть його зліва від десяткової крапки.
- Якщо немає «і», напишіть «0» з десятковою крапкою праворуч.
Крок 3. Переведіть слова після «і» в число праворуч від десяткової крапки. Запишіть число в пробілах - поставивши остаточну цифру на останнє місце.
Крок 4. Заповніть нулі для власників місць у міру необхідності.
Друга куля на кроці 2 потрібна для десяткових знаків, які не мають цілої числової частини, як «дев'ять тисячних». Ми розпізнаємо їх за словами, які вказують місце після десяткового числа - наприклад, «десяті» або «соті». Оскільки немає цілого числа, немає «і». Починаємо з того, що ставимо нуль зліва від десяткового і продовжуємо заповнювати цифри праворуч, як ми це робили вище.
Запишіть двадцять чотири тисячні частки як десяткове число.
Рішення
| Шукайте слово «і». | Немає «і», тому почніть з 0. |
| Праворуч від десяткової крапки поставте три знака після коми для тисячних. |  |
| Напишіть число 24 з 4 в тисячному місці. |  |
| Поставте нулі як заповнювачі в решту знаків після коми. | 0,024 |
Отже, двадцять чотири тисячні написано 0,024
Запишіть як десяткове число: пятьдесят вісім тисячних.
- Відповідь
-
0,058
Запишіть як десяткове число: шестьдесят сім тисячних.
- Відповідь
-
0.067
Перш ніж перейти до наступної мети, подумайте ще раз про гроші. Ми знаємо, що $1 - це те ж саме, що і $1,00. Те, як ми пишемо $1 (або $1.00), залежить від контексту. Таким же чином, цілі числа можуть бути записані як десяткові числа з такою кількістю нулів, скільки потрібно праворуч від десяткової.
\[\begin{split} 5 & = 5.0 \qquad \quad -2 = -2.0 \\ 5 & = 5.00 \qquad \; \; -2 = -2.00 \\ 5 & = 5.000 \qquad -2 = -2.000 \\ & \qquad \qquad and \; so \; on \ldots \end{split}\]
Перетворення десяткових дробів на дроби або мішані числа
Нам часто потрібно переписувати десяткові числа як дроби або мішані числа. Давайте повернемося до нашого обіднього замовлення, щоб побачити, як ми можемо перетворити десяткові числа в дроби. Ми знаємо, що $5.03 означає 5 доларів і 3 центи. Так як в одному доларі 100 центів, 3\(\dfrac{3}{100}\) центи означає долар, тому 0,03 =\(\dfrac{3}{100}\).
Переводимо десяткові числа в дроби, визначаючи місце найдальшої правої цифри. У десятковому 0.03 3 знаходиться на сотих місцях, тому 100 - знаменник дробу, еквівалентний 0,03.
\[0.03 = \dfrac{3}{100} \nonumber\]
Для нашого обіду $5,03 ми можемо написати десяткове 5.03 як змішане число.
\[5.03 = 5 \dfrac{3}{100} \nonumber\]
Зверніть увагу, що коли число зліва від десяткового числа дорівнює нулю, ми отримуємо правильний дріб. Коли число зліва від десяткового числа не дорівнює нулю, ми отримуємо змішане число.
Крок 1. Подивіться на число ліворуч від десяткового числа.
- Якщо він дорівнює нулю, десяткове число перетворюється на правильний дріб.
- Якщо він не дорівнює нулю, десяткове число перетворюється в змішане число.
- Напишіть ціле число.
Крок 2. Визначте місце значення кінцевої цифри.
Крок 3. Запишіть дріб.
- numerator — «числа» праворуч від десяткової крапки
- знаменник — значення місця, відповідне кінцевій цифрі
Крок 4. Спростіть дріб, якщо це можливо.
Запишіть кожне з наступних десяткових чисел у вигляді дробу або мішаного числа: (a) 4.09 (b) 3.7 (c) −0.286
Рішення
(а) 4.09
| Ліворуч від десяткової крапки знаходиться 4. Запишіть «4» як цілу числову частину мішаного числа. |  |
| Визначте місце значення кінцевої цифри. |  |
| Запишіть дріб. Запишіть 9 в чисельнику, оскільки це число праворуч від десяткової крапки. |  |
| Запишіть 100 в знаменнику як місце кінцевої цифри, 9, сотих. | \(4 \dfrac{9}{100}\) |
| Дріб знаходиться в найпростішому вигляді. | Отже, 4.09 =\(4 \dfrac{9}{100}\) |
Ви помітили, що кількість нулів в знаменнику збігається з кількістю десяткових знаків?
(б) 3.7
| Ліворуч від десяткової крапки знаходиться 3. Напишіть «3» як цілу цифрову частину змішаного числа. |  |
| Визначте місце значення кінцевої цифри. |  |
| Запишіть дріб. Запишіть 7 в чисельнику, оскільки це число праворуч від десяткової крапки. |  |
| Запишіть 10 в знаменнику як місце кінцевої цифри, 7, десятих. | \(3 \dfrac{7}{10}\) |
| Дріб знаходиться в найпростішому вигляді. | Отже, 3,7 =\(3 \dfrac{7}{10}\) |
(c) −0,286
| Ліворуч від десяткової крапки знаходиться 0. Напишіть негативний знак перед дробом. |  |
| Визначте місце значення кінцевої цифри і запишіть її в знаменник. |  |
| Запишіть дріб. Запишіть 286 в чисельнику, оскільки це число праворуч від десяткової крапки. Напишіть 1000 в знаменнику як місце кінцевої цифри, 6, тисячні. | \(- \dfrac{286}{1000}\) |
| Прибираємо загальний коефіцієнт 2 для спрощення дробу. | \(- \dfrac{143}{500}\) |
Запишіть як дріб або мішане число. Спростіть відповідь, якщо це можливо. (а) 5.3 (б) 6.07 (c) −0,234
- Відповідь на
-
\(5 \frac{3}{10}\)
- Відповідь б
-
\(6 \frac{7}{100}\)
- Відповідь c
-
\(-\frac{234}{1000}\)
Запишіть як дріб або мішане число. Спростіть відповідь, якщо це можливо. (а) 8.7 (б) 1.03 (c) −0,024
- Відповідь на
-
\(8 \frac{7}{10}\)
- Відповідь б
-
\(1 \frac{3}{100}\)
- Відповідь c
-
\(- \frac{24}{1000}\)
