4.9: Розв'язування рівнянь з дробами

Last updated
Save as PDF

Page ID: 57343

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Скасування віднімання

Ми все ще можемо додати однакову кількість до обох сторін рівняння, не змінюючи рішення.

Приклад 1

Вирішити для х:$x - \frac{5}{6} = \frac{1}{3}$.

Рішення

Щоб «скасувати» віднімання 5/6, додайте 5/6 до обох сторін рівняння та спростіть.

\[ \begin{aligned} x - \frac{5}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Original equation.}} \\ x - \frac{5}{6} + \frac{5}{6} = \frac{1}{3} + \frac{5}{6} ~ & \textcolor{red}{ \text{ Add } \frac{5}{6} \text{ to both sides.}} \\ x = \frac{1 \cdot 2}{3 \cdot 2} + \frac{5}{6} ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 6.}} \\ x = \frac{2}{6} + \frac{5}{6} ~ & \textcolor{red}{ \text{ Simplify.}} \\ x = \frac{7}{6} ~ & \textcolor{red}{ \text{ Add.}} \end{aligned}\nonumber \]

Цілком прийнятно залишити свою відповідь як неправильний дріб. Якщо ви хочете, або якщо вам доручено це зробити, ви можете змінити свою відповідь на змішаний дріб (7 ділиться на 6 дорівнює 1 із залишком 1). Тобто$x = 1 \frac{1}{6}$.

Перевірка рішення

Замініть 7/6 для x у вихідному рівнянні та спростіть.

\[ \begin{aligned} x - \frac{5}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{7}{6} - \frac{5}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Substitute 7/6 for } x.} \\ \frac{2}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Subtract.}} \\ \frac{1}{3} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Reduce.}} \end{aligned}\nonumber \]

Оскільки останнє твердження є істинним, ми робимо висновок, що 7/6 є розв'язком рівняння x − 5/6 = 1/3.

Скасування додавання

Ви все одно можете відняти однакову величину з обох сторін рівняння, не змінюючи рішення.

Приклад 2

Вирішити для х:$x + \frac{2}{3} = - \frac{3}{5}$.

Рішення

Щоб «скасувати» додавання 2/3, відніміть 2/3 з обох сторін рівняння і спростіть.

\[ \begin{aligned} x + \frac{2}{3} = - \frac{3}{5} ~ & \textcolor{red}{ \text{ Original equation.}} \\ x + \frac{2}{3} - \frac{2}{3} = - \frac{3}{5} - \frac{2}{3} ~ & \textcolor{red}{ \text{ Subtract } \frac{2}{3} \text{ from both sides.}} \\ x = - \frac{3 \cdot 3}{5 \cdot 3} - \frac{2 \cdot 5}{3 \cdot 5} ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 15.}} \\ x = - \frac{9}{15} - \frac{10}{15} ~ & \textcolor{red}{ \text{ Simplify.}} \\ x = - \frac{19}{15} ~ & \textcolor{red}{ \text{ Subtract.}} \end{aligned}\nonumber \]

Читачам рекомендується перевірити це рішення в оригінальному рівнянні.

Вправа

Вирішити для х:$x + \frac{3}{4} = - \frac{1}{2}$

Відповідь: −5/4

Скасування множення

Ми «скасуємо» множення діленням. Наприклад, щоб вирішити рівняння 2 х = 6, ми б розділили обидві сторони рівняння на 2. Подібним чином ми могли б розділити обидві сторони рівняння

\[ \frac{3}{5} x = \frac{4}{10}\nonumber \]

на 3/5. Однак ефективніше скористатися взаємністю. Для зручності нагадуємо читачам мультиплікативне обернене властивість.

Мультиплікативна обернена властивість

Нехай a /b буде будь-яким дробом. Число b/a називається мультиплікативним оберненим або зворотним від a/b. Твір зворотних - 1.

\[ \frac{a}{b} \cdot \frac{b}{a} = 1.\nonumber \]

Давайте покладемо наші знання про взаємні дії на роботу.

Приклад 3

Вирішити для х:$\frac{3}{5}x = \frac{4}{10}$.

Рішення

Щоб «скасувати» множення на 3/5, помножте обидві сторони на зворотну 5/3 і спростіть.

\[ \begin{aligned} \frac{3}{5} x = \frac{4}{10} ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{5}{3} \left( \frac{3}{5} x \right) = \frac{5}{3} \left( \frac{4}{10} \right) & ~ \textcolor{red}{ \text{ Multiply both sides by 5/3.}} \\ \left( \frac{5}{3} \cdot \frac{3}{5} \right) x = \frac{20}{30} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, use the associative property to regroup.} \\ \text{ On the right, multiply.} \end{array}} \\ 1x = \frac{2}{3} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, } \frac{5}{3} \cdot \frac{3}{5} = 1. \\ \text{ On the right, reduce: } \frac{20}{30} = \frac{2}{3}. \end{array}} \\ x = \frac{2}{3} ~ & \textcolor{red}{ \text{ On the left, } 1x = x.} \end{aligned}\nonumber \]

Перевірка рішення

Замініть 2/3 для x у вихідному рівнянні та спростіть.

\[ \begin{aligned} \frac{3}{5} x = \frac{4}{10} ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{3}{5} \left( \frac{2}{3} \right) = \frac{4}{10} ~ & \textcolor{red}{ \text{ Substitute 2/3 for }x.} \\ \frac{6}{15} = \frac{4}{10} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ \frac{2}{5} = \frac{2}{5} ~ & \textcolor{red}{ \text{ Reduce both sides to lowest terms.}} \end{aligned}\nonumber \]

Оскільки це останнє твердження вірно, робимо висновок, що 2/3 - це рішення рівняння (3/5) х = 4/10.

Вправа

Вирішити для y:$ \frac{2}{3} y = \frac{4}{5}$

Відповідь: 6/5

Приклад 4

Вирішити для х:$- \frac{8}{9} x = \frac{5}{18}$.

Рішення

Щоб «скасувати» множення на −8/9, помножте обидві сторони на зворотний −9/8 і спростіть.

\[ \begin{aligned} - \frac{8}{9} x = \frac{5}{18} ~ & \textcolor{red}{ \text{ Original equation.}} \\ - \frac{9}{8} \left( - \frac{8}{9} x \right) = - \frac{9}{8} \left( \frac{5}{18} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by } -9/8.} \\ \left[ - \frac{9}{8} \cdot \left( - \frac{8}{9} \right) \right] x = - \frac{3 \cdot 3}{2 \cdot 2 \cdot 2} \cdot \frac{5}{2 \cdot 3 \cdot 3} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, use the associative property to regroup.} \\ \text{ On the right, prime factor.} \end{array}} 1x = \frac{ \cancel{3} \cdot \cancel{3}}{2 \cdot 2 \cdot 2} \cdot \frac{5}{2 \cdot \cancel{3} \cdot \cancel{3}} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, } - \frac{9}{8} \cdot \left( - \frac{8}{9} \right) = 1. \\ \text{ On the right, cancel common factors.} \end{array}} \\ x = - \frac{5}{16} ~ & \textcolor{red}{ \text{ On the left, } 1x = x. \text{ Multiply on the right.}} \end{aligned}\nonumber \]

Читачам рекомендується перевірити це рішення в оригінальному рівнянні.

Вправа

Вирішити для z:$− \frac{2}{7} z = \frac{4}{21}$

Відповідь: −2/3

Очищення дробів від рівняння

Хоча методика, продемонстрована в попередніх прикладах, є твердою математичною технікою, робота з дробами в рівнянні не завжди є найбільш ефективним використанням вашого часу.

Очищення дробів від рівняння

Щоб очистити всі дроби з рівняння, помножте обидві сторони рівняння на найменш спільний знаменник дробів, які фігурують у рівнянні.

Давайте втілимо цю ідею на роботу.

Приклад 5

У прикладі 1 нам було запропоновано вирішити наступне рівняння для x:

\[x - \frac{5}{6} = \frac{1}{3}.\nonumber \]

Знайдіть хвилинку, щоб переглянути техніку рішення в прикладі 1. Тепер ми вирішимо це рівняння, попередньо очистивши всі дроби з рівняння.

Рішення

Помножте обидві сторони рівняння на найменш спільний знаменник для дробів, що фігурують у рівнянні.

\[ \begin{aligned} x - \frac{5}{6}= \frac{1}{3} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 6 \left( x - \frac{5}{6} \right) = 6 \left( \frac{1}{3} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 6.}} \\ 6x - 6 \left( \frac{5}{6} \right) = 6 \left( \frac{1}{3} \right) ~ & \textcolor{red}{ \text{ Distribute the 6.}} \\ 6x-5 = 2 ~ & \textcolor{red}{ \text{ On each side, multiply first.}} \\ ~ & \textcolor{red}{6 \left( \frac{5}{6} \right) = 5 \text{ and } 6 \left( \frac{1}{3} \right) = 2.} \end{aligned}\nonumber \]

Зверніть увагу, що рівняння тепер повністю зрозуміле від дробів, що робить його набагато простішим рівнянням для вирішення.

\[ \begin{aligned} 6x - 5 + 5 = 2 + 5 ~ & \textcolor{red}{ \text{ Add 5 to both sides.}} \\ 6x = 7 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{6x}{6} = \frac{7}{6} ~ & \textcolor{red}{ \text{ Divide both sides by 6.}} \\ x = \frac{7}{6} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Зауважте, що це те саме рішення, яке можна знайти в прикладі 1.

Вправа

Вирішити для t:$t - \frac{2}{7} = - \frac{1}{4}$

Відповідь: 1/28

Приклад 6

У прикладі 4 нам було запропоновано вирішити наступне рівняння для x.

\[- \frac{8}{9}x = \frac{5}{18}\nonumber \]

Знайдіть хвилинку, щоб переглянути рішення в прикладі 4. Тепер ми вирішимо це рівняння, попередньо очистивши всі дроби з рівняння.

Рішення

Помножте обидві сторони рівняння на найменш спільний знаменник для дробів, які фігурують у рівнянні.

\[ \begin{aligned} - \frac{8}{9} x = \frac{5}{18} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 18 \left( - \frac{8}{9} x \right) = 18 \left( \frac{5}{18} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 18.}} \\ -16x=5 ~ & \textcolor{red}{ \text{ On each side, cancel and multiply.}} \\ ~ & \textcolor{red}{ 18 \left( - \frac{8}{9} \right) = -16 \text{ and } 18 \left( \frac{5}{18} \right) = 5.} \end{aligned}\nonumber \]

Зверніть увагу, що рівняння тепер повністю вільне від дробів. Продовжуючи,

\[ \begin{aligned} \frac{-16x}{-16} = \frac{5}{-16} ~ & \textcolor{red}{ \text{ Divide both sides by } -16.} \\ x = - \frac{5}{16} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Зауважте, що це те саме, що і рішення, знайдене в прикладі 4.

Вправа

Вирішіть для вас:

\[ - \frac{7}{9} u = \frac{14}{27}\nonumber \]

Відповідь: −2/3

Приклад 7

Вирішити для х:$\frac{2}{3}x + \frac{3}{4} = \frac{1}{2}$.

Рішення

Помножте обидві сторони рівняння на найменш спільний знаменник для дробів, що фігурують у рівнянні.

\[ \begin{aligned} \frac{2}{3} x + \frac{3}{4} = \frac{1}{2} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 12 \left( \frac{2}{3} x + \frac{3}{4} = \right) = 12 \left( \frac{1}{2} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 12.}} \\ 12 \left( \frac{2}{3}x \right) + 12 \left( \frac{3}{4} \right) = 12 \left( \frac{1}{2} \right) ~ & \textcolor{red}{ \text{ On the left, distribute 12.}} \\ 8x + 9 = 6 ~ & \textcolor{red}{ \text{ Multiply: } 12 \left( \frac{2}{3} x \right) = 8x, ~ 12 \left( \frac{3}{4} \right) = 9,} \\ ~ & \textcolor{red}{ \text{ and } 12 \left( \frac{1}{2} \right) = 6.} \end{aligned}\nonumber \]

Зверніть увагу, що рівняння тепер повністю вільне від дробів. Нам потрібно виділити члени, що містять x на одній стороні рівняння.

\[ \begin{aligned} 8x + 9 - 9 = 6 - 9 ~ & \textcolor{red}{ \text{ Subtract 9 from both sides.}} \\ 8x = - 3 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{8x}{8} = \frac{-3}{8} ~ & \textcolor{red}{ \text{ Divide both sides by 8.}} \\ x = - \frac{3}{8} ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]

Читачам рекомендується перевірити це рішення в оригінальному рівнянні.

Вправа

Вирішити для r:$\frac{3}{4} r + \frac{2}{3} = \frac{1}{2}$

Відповідь: −2/9

Приклад 8

Вирішити для х:$ \frac{2}{3} - \frac{3x}{4} = \frac{x}{2} - \frac{1}{8}.$

Рішення

Помножте обидві сторони рівняння на найменш спільний знаменник для дробів у рівнянні.

\[ \begin{aligned} \frac{2}{3} - \frac{3x}{4} = \frac{x}{2} - \frac{1}{8} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 24 \left( \frac{2}{3} - \frac{3x}{4} \right) = 24 \left( \frac{x}{2} - \frac{1}{8} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 24.}} \\ 24 \left( \frac{2}{3} \right) - 24 \left( \frac{3x}{4} \right) = 24 \left( \frac{x}{2} \right) - 24 \left( \frac{1}{8} \right) ~ & \textcolor{red}{ \text{ On both sides, distribute 24.}} \\ 16 - 18x = 12x - 3 ~ & \textcolor{red}{ \text{ Left: } 24 \left( \frac{2}{3} \right) = 16, ~ 24 \left( \frac{3x}{4} \right) = 18x.} \\ ~ & \textcolor{red}{ \text{ Right: } 24 \left( \frac{x}{2} \right) = 12x, ~ 24 \left( \frac{1}{8} \right) = 3.} \end{aligned}\nonumber \]

\[ \begin{aligned} 16 - 18x - 12x = 12x - 3 - 12x ~ & \textcolor{red}{ \text{ Subtract } 12x \text{ from both sides.}} \\ 16 - 30x = -3 ~ & \textcolor{red}{ \begin{aligned} \text{ Left: } -18x - 12x = -30x. \\ \text{ Right: } 12x - 12x = 0. \end{aligned}} \\ 16 - 30x - 16 = -3 - 16 ~ & \textcolor{red}{ \text{ Subtract 16 from both sides.}} \\ -30x = -19 ~ & \textcolor{red}{ \begin{aligned} \text{ Left: } 16-16=0. \\ \text{ Right: } -3 - 16 = -19. \end{aligned}} \\ \frac{-30x}{-30} = \frac{-19}{-30} ~ & \textcolor{red}{ \text{ Divide both sides by } -30.} \\ x = \frac{19}{30} ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]

Читачам рекомендується перевірити це рішення в оригінальному рівнянні.

Вправа

Вирішити для s:$ \frac{3}{2} - \frac{2s}{5} = \frac{s}{3} - \frac{1}{5}$.

Відповідь: Додайте сюди тексти. Не видаляйте цей текст спочатку.

Додатки

Давайте розглянемо деякі програми, які включають рівняння, що містять дроби. Для зручності повторюємо Вимоги до вирішення проблем Word.

Вимоги до вирішення проблем Word

Налаштуйте словник змінних. Ви повинні повідомити своїм читачам, що представляє кожна змінна у вашій проблемі. Це може бути досягнуто кількома способами:
1. Такі заяви, як «Нехай P представляє периметр прямокутника».
2. Позначення невідомих значень змінними в таблиці.
3. Маркування невідомих величин в ескізі або схемі.
Налаштуйте рівняння. Кожне рішення проблеми зі словом має містити ретельно розроблене рівняння, яке точно описує обмеження в постановці задачі.
Розв'яжіть рівняння. Ви завжди повинні вирішувати рівняння, встановлене на попередньому кроці.
Дайте відповідь на питання. Цей крок легко не помітити. Наприклад, проблема може запитати вік Джейн, але рішення вашого рівняння дає вік сестри Джейн Ліз. Переконайтеся, що ви відповіли на оригінальне запитання, поставлене в проблемі. Ваше рішення має бути записано в реченні з відповідними одиницями 5. Озирніться назад. Важливо зазначити, що цей крок не означає, що ви повинні просто перевірити своє рішення у своєму рівнянні. Зрештою, можливо, ваше рівняння неправильно моделює ситуацію задачі, тож ви можете мати правильне рішення неправильного рівняння. Важливе питання: «Чи має сенс ваша відповідь на основі слів в оригінальній постановці проблеми».

Приклад 9

У третій чверті баскетбольного матчу диктори повідомили натовпу, що відвідуваність гри склала 12 250. Якщо це дві третини місткості, знайдіть повну місткість для баскетбольної арени.

Рішення

Ми дотримуємося вимог до вирішення проблем Word.

1. Налаштуйте словник змінних. Нехай F представляють повну місткість сидіння. Примітка: Набагато краще використовувати змінну, яка «звучить як» кількість, яку вона представляє. У цьому випадку дозволити F представляти повну місткість сидіння набагато більш описовим, ніж використання x для представлення повної місткості сидіння.

2. Налаштуйте рівняння. Дві третини повної місткості - 12 250 місць.

\[ \begin{aligned} \colorbox{cyan}{Two-thirds} & \text{ of } & \colorbox{cyan}{Full Seating Capacity} & \text{ is } & 12,250 \\ \frac{2}{3} & \cdot & F & = & 12,250 \end{aligned}\nonumber \]

Отже, рівняння

\[ \frac{2}{3} F = 12250.\nonumber \]

3. Розв'яжіть рівняння. Помножте обидві сторони на 3, щоб очистити дроби, а потім вирішити.

\[ \begin{aligned} \frac{2}{3} F = 12250 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 3 \left( \frac{2}{3} F \right) = 3(12250) ~ & \textcolor{red}{ \text{ Multiply both sides by 3.}} \\ 2F = 36750 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{2F}{2} = \frac{36750}{2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ F = 18375 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]

4. Дайте відповідь на питання. Повна місткість місць становить 18 375.

5. Озирніться назад. Слова проблеми стверджують, що 2/3 місткості сидіння становить 12 250. Давайте візьмемо дві третини нашої відповіді і подивимося, що ми отримаємо.

\[ \begin{aligned} \frac{2}{3} \cdot 18375 & = \frac{2}{3} \cdot \frac{18375}{1} \\ & = \frac{2}{3} \cdot \frac{3 \cdot 6125}{1} \\ & = \frac{2}{ \cancel{3}} \cdot \frac{ \cancel{3} \cdot 6125}{1} \\ & = 12250 \end{aligned}\nonumber \]

Це правильна відвідуваність, тому наше рішення правильне.

Вправа

Відвідуваність гри «Селтікс» склала 9 510. Якщо це 3/4 місткості, яка місткість арени «Селтікс»?

Відповідь: 12 680

приклад 10

Площа трикутника становить 20 квадратних дюймів. Якщо довжина підстави дорівнює$2 \frac{1}{2}$ дюймам, знайдіть висоту (висоту) трикутника.

Рішення

Ми дотримуємося вимог до вирішення проблем Word.

1. Налаштуйте словник змінних. Наш змінний словник буде мати форму добре позначеної діаграми.

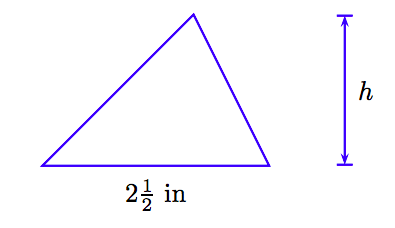
$Знімок екрана 2019-09-09 о 10.44.05 AM.png$

2. Налаштуйте рівняння. Площа A трикутника з основою b і висотою h дорівнює

\[A = \frac{1}{2} bh.\nonumber \]

Підставляємо A = 20 і b =$2 \frac{1}{2}$.

\[20 = \frac{1}{2} \left( 2 \frac{1}{2} \right) h.\nonumber \]

3. Розв'яжіть рівняння. Змішайте змішану фракцію на неправильну, потім спростіть.

\[ \begin{aligned} 20 = \frac{1}{2} \left( 2 \frac{1}{2} \right) h ~ & \textcolor{red}{ \text{ Original equation.}} \\ 20 = \frac{1}{2} \left( \frac{5}{2} \right) h ~ & \textcolor{red}{ \text{ Mixed to improper: } 2 \frac{1}{2} = \frac{5}{2}.} \\ 20 = \left( \frac{1}{2} \cdot \frac{5}{2} \right) h ~ & \textcolor{red}{ \text{ Associative property.}} \\ 20 = \frac{5}{4} h ~ & \textcolor{red}{ \text{ Multiply: } \frac{1}{2} \cdot \frac{5}{2} = \frac{5}{4}.} \end{aligned}\nonumber \]

Тепер помножте обидві сторони на 4/5 і вирішіть.

\[ \begin{aligned} \frac{4}{5} (20) = \frac{4}{5} \left( \frac{5}{4} h \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 4/5.}} \\ 16 = h ~ & \textcolor{red}{ \text{ Simplify: } \frac{4}{5} (20) = 16} \\ ~ & \textcolor{red}{ \text{ and } \frac{4}{5} \cdot \frac{5}{4} = 1.} \end{aligned}\nonumber \]

4. Дайте відповідь на питання. Висота трикутника - 16 дюймів.

5. Озирніться назад. Якщо висота становить 16 дюймів, а основа -$2 \frac{1}{2}$ дюйми, то площа

\[ \begin{aligned} A & = \frac{1}{2} \left( 2 \frac{1}{2} \right) (16) \\ & = \frac{1}{2} \cdot \frac{5}{2} \cdot \frac{16}{1} \\ & = \frac{5 \cdot 16}{2 \cdot 2} \\ & = \frac{(5) \cdot (2 \cdot 2 \cdot 2 \cdot 2)}{(2) \cdot (2)} \\ & = \frac{5 \cdot \cancel{2} \cdot \cancel{2} \cdot 2 \cot 2}{ \cancel{2} \cdot \cancel{2}} & = 20 \end{aligned}\nonumber \]

Це правильна площа (20 квадратних дюймів), тому наше рішення правильне.

Вправа

Площа трикутника становить 161 квадратний фут. Якщо основа трикутника вимірює$40 \frac{1}{4}$ фути, знайдіть висоту трикутника.

Відповідь: 8 футів

Вправи

1. 1/4 є розв'язком рівняння$x + \frac{5}{8} = \frac{5}{8}$?

2. 1/4 є розв'язком рівняння$x + \frac{1}{3} = \frac{5}{12}$?

3. Чи є −8/15 розв'язком рівняння$\frac{1}{4} x = − \frac{1}{15}$?

4. Чи є −18/7 розв'язком рівняння$− \frac{3}{8} x = \frac{25}{28}$?

5. 1/2 є розв'язком рівняння$x + \frac{4}{9} = \frac{17}{18}$?

6. 1/3 є розв'язком рівняння$x + \frac{3}{4} = \frac{13}{12}$?

7. Чи є 3/8 розв'язком рівняння$x − \frac{5}{9} = − \frac{13}{72}$?

8. 1/2 є розв'язком рівняння$x − \frac{3}{5} = − \frac{1}{10}$?

9. Чи є 2/7 розв'язком рівняння$x − \frac{4}{9} = − \frac{8}{63}$?

10. Чи є 1/9 розв'язком рівняння$x − \frac{4}{7} = − \frac{31}{63}$?

11. 8/5 є розв'язком рівняння$ \frac{11}{14}x = \frac{44}{35}$?

12. 16/9 є розв'язком рівняння$\frac{13}{18} x = \frac{104}{81}$?

У Вправи 13-24 розв'яжіть рівняння і спростіть свою відповідь.

13. $2x − 3=6x + 7$

14. $9x − 8 = −9x − 3$

15. $−7x +4=3x$

16. $6x +9= −6x$

17. $−2x = 9x − 4$

18. $−6x = −9x + 8$

19. $−8x = 7x − 7$

20. $−6x = 5x + 4$

21. $−7x +8=2x$

22. $−x − 7=3x$

23. $−9x +4=4x − 6$

24. $−2x +4= x − 7$

У Вправи 25-48 розв'яжіть рівняння і спростіть свою відповідь.

25. $x + \frac{3}{2 = \frac{1}{2}$

26. $x − \frac{3}{4} = \frac{1}{4}$

27. $− \frac{9}{5} x = \frac{1}{2}$

28. $\frac{7}{3} x = − \frac{7}{2}$

29. $\frac{3}{8} x = \frac{8}{7}$

30. $− \frac{1}{9} x = − \frac{3}{5}$

31. $\frac{2}{5} x = − \frac{1}{6}$

32. $\frac{1}{6} x = \frac{2}{9}$

33. $− \frac{3}{2} x = \frac{8}{7}$

34. $− \frac{3}{2} x = − \frac{7}{5}$

35. $x + \frac{3}{4} = \frac{5}{9}$

36. $x − \frac{1}{9} = − \frac{3}{2}$

37. $x − \frac{4}{7} = \frac{7}{8}$

38. $x + \frac{4}{9} = − \frac{3}{4}$

39. $x + \frac{8}{9} = \frac{2}{3}$

40. $x − \frac{5}{6} = \frac{1}{4}$

41. $x + \frac{5}{2} = − \frac{9}{8}$

42. $x + \frac{1}{2} = \frac{5}{3}$

43. $− \frac{8}{5} x = \frac{7}{9}$

44. $− \frac{3}{2} x = − \frac{5}{9}$

45. $x − \frac{1}{4} = − \frac{1}{8}$

46. $x − \frac{9}{2} = − \frac{7}{2}$

47. $− \frac{1}{4} x = \frac{1}{2}$

48. $− \frac{8}{9} x = − \frac{8}{3}$

У Вправи 49-72 розв'яжіть рівняння і спростіть свою відповідь.

49. $− \frac{7}{3} x − \frac{2}{3} = \frac{3}{4} x + \frac{2}{3}$

50. $\frac{1}{2} x − \frac{1}{2} = \frac{3}{2} x + \frac{3}{4}$

51. $− \frac{7}{2} x − \frac{5}{4} = \frac{4}{5}$

52. $− \frac{7}{6} x + \frac{5}{6} = − \frac{8}{9}$

53. $− \frac{9}{7} x + \frac{9}{2} = − \frac{5}{2}$

54. $\frac{5}{9} x − \frac{7}{2} = \frac{1}{4}$

55. $\frac{1}{4} x − \frac{4}{3} = − \frac{2}{3}$

56. $\frac{8}{7} x + \frac{3}{7} = \frac{5}{3}$

57. $\frac{5}{3} x + \frac{3}{2} = − \frac{1}{4}$

58. $\frac{1}{2} x − \frac{8}{3} = − \frac{2}{5}$

59. $− \frac{1}{3} x + \frac{4}{5} = − \frac{9}{5} x − \frac{5}{6}$

60. $− \frac{2}{9} x − \frac{3}{5} = \frac{4}{5} x − \frac{3}{2}$

61. $− \frac{4}{9} x − \frac{8}{9} = \frac{1}{2} x − \frac{1}{2}$

62. $− \frac{5}{4} x − \frac{5}{3} = \frac{8}{7} x + \frac{7}{3}$

63. $\frac{1}{2} x − \frac{1}{8} = − \frac{1}{8} x + \frac{5}{7}$

64. $− \frac{3}{2} x + \frac{8}{3} = \frac{7}{9} x − \frac{1}{2}$

65. $− \frac{3}{7} x − \frac{1}{3} = − \frac{1}{9}$

66. $\frac{2}{3} x + \frac{2}{9} = − \frac{9}{5}$

67. $− \frac{3}{4} x + \frac{2}{7} = \frac{8}{7} x − \frac{1}{3}$

68. $\frac{1}{2} x + \frac{1}{3} = − \frac{5}{2} x − \frac{1}{4}$

69. $− \frac{3}{4} x − \frac{2}{3} = − \frac{2}{3} x − \frac{1}{2}$

70. $\frac{1}{3} x − \frac{5}{7} = \frac{3}{2} x + \frac{4}{3}$

71. $− \frac{5}{2} x + \frac{9}{5} = \frac{5}{8}$

72. $\frac{9}{4} x + \frac{4}{3} = − \frac{1}{6}$

73. На місцевому футбольному матчі диктори повідомили натовпу, що відвідуваність гри склала 4,302. Якщо це 2/9 місткості, знайдіть повну місткість для футбольного стадіону.

74. На місцевому баскетбольному матчі диктори повідомили натовпу, що відвідуваність гри склала 5,394. Якщо це 2/7 місткості, знайдіть повну місткість для баскетбольного стадіону.

75. Площа трикутника становить 51 квадратний дюйм. Якщо довжина підстави дорівнює$8 \frac{1}{2}$ дюймам, знайдіть висоту (висоту) трикутника.

76. Площа трикутника становить 20 квадратних дюймів. Якщо довжина підстави дорівнює$2 \frac{1}{2}$ дюймам, знайдіть висоту (висоту) трикутника.

77. Площа трикутника становить 18 квадратних дюймів. Якщо довжина підстави дорівнює$4 \frac{1}{2}$ дюймам, знайдіть висоту (висоту) трикутника.

78. Площа трикутника становить 44 квадратних дюйма. Якщо довжина підстави дорівнює$5 \frac{1}{2}$ дюймам, знайдіть висоту (висоту) трикутника.

79. На місцевому хокейному матчі диктори повідомили натовпу, що відвідуваність гри склала 4,536. Якщо це 2/11 місткості, знайдіть повну місткість для хокейного стадіону.

80. На місцевому футбольному матчі диктори повідомили натовпу, що відвідуваність гри склала 6,970. Якщо це 2/7 місткості, знайдіть повну місткість для футбольного стадіону.

81. Пірати. Близько третини світових піратських атак у 2008 році відбулися біля узбережжя Сомалі. Якщо біля узбережжя Сомалі було 111 піратських атак, оцініть кількість піратських атак у всьому світі в 2008 році.

82. Ядерний арсенал. США і Росія домовилися скоротити ядерні арсенали далекої ядерної зброї приблизно на третину, до 1 550. Скільки ядерних озброєнь далекої дальності існує зараз? Associated Прес-Times-Стандарт 04/04/10 Ядерна серцевина стурбована ракетними скороченнями.

83. Насіннєвий звід. The Svalbard Global Seed Vault зібрав півмільйона зразків насіння і тепер містить щонайменше третину світового насіння сільськогосподарських культур. Оцініть загальну кількість насіння світових культур. Associated Press-Times-Стандарт 03/15/10 Норвегія кінець дня насіння сховища досягає півмільйона позначки.

84. Вантажний потяг. Поїзд Union Pacific довжиною в три з половиною милі приблизно в 2 1 2 рази перевищує довжину типового вантажного поїзда. Скільки триває типовий вантажний поїзд? Associated Press-Times-Standard 01/13/10 Незвично довгий поїзд викликає проблеми безпеки.

Відповіді

1. Ні

3. Ні

5. Так

7. Так

9. Ні

11. Так

13. $− \frac{5}{2}$

15. $\frac{2}{5}$

17. $\frac{4}{11}$

19. $\frac{7}{15}$

21. $\frac{8}{9}$

23. $\frac{10}{13}$

25. $−1$

27. $− \frac{5}{18}$

29. $\frac{64}{21}$

31. $− \frac{5}{12}$

33. $− \frac{16}{21}$

35. $− \frac{7}{36}$

37. $\frac{81}{56}$

39. $− \frac{2}{9}$

41. $− \frac{29}{8}$

43. $− \frac{35}{72}$

45. $\frac{1}{8}$

47. $−2$

49. $− \frac{16}{37}$

51. $− \frac{41}{70}$

53. $\frac{49}{9}$

55. $\frac{8}{3}$

57. $− \frac{21}{20}$

59. $− \frac{49}{44}$

61. $− \frac{7}{17}$

63. $\frac{47}{35}$

65. $− \frac{14}{27}$

67. $\frac{52}{159}$

69. $− 2$

71. $\frac{47}{100}$

73. 19 359

75. 12

77. 8

79. 24 948

81. У всьому світі було близько 333 нападу піратів.

83. 1 500 000