3.2: Оцінка алгебраїчних виразів

У цьому розділі ми будемо оцінювати алгебраїчні вирази для заданих значень змінних, що містяться у виразах. Ось кілька простих порад, які допоможуть вам досягти успіху.

Поради щодо оцінки алгебраїчних виразів

1. Замініть усі входження змінних у виразі відкритими дужками. Залиште місце між дужками, щоб підставити задане значення змінної.
2. Підставляємо задані значення змінних у відкриті дужки, підготовлені на першому кроці.
3. Оцінити отриманий вираз відповідно до Правил Керівного Порядку операцій.

Почнемо з прикладу.

Приклад 1

Оцініть вираз$x^2 − 2xy + y^2$ в$x = −3$ і$y = 2$.

Рішення

Дотримуючись «Поради щодо оцінки алгебраїчних виразів», спочатку замініть усі входження змінних у виразі x ² − 2 xy + y ² відкритими дужками.

$$x^2 -2xy + y^2 = ( ~ )^2 -2(~)(~) + ( ~ )^2 \nonumber\nonumber$$

По-друге, замініть кожну змінну на задане значення, а по-третє, дотримуйтесь «Правил, що керівний порядок операцій», щоб оцінити отриманий вираз.

$$\begin{aligned} x^2 -2xy + y^2 ~ & \textcolor{red}{ \text{ Original expression.}} \\ =( \textcolor{red}{-3} )^2 -2 ( \textcolor{red}{-3})( \textcolor{red}{2}) + (\textcolor{red}{2})^2 ~ & \textcolor{red}{ \text{ Substitute } -3 \text{ for } x \text{and 2 for }y.} \\ =9-2(-3)(2)+4 ~ & \textcolor{red}{ \text{ Evaluate exponents first.}} \\ = 9-(-6)(2)+4 ~ & \textcolor{red}{ \text{ Left to right, multiply } 2(-3)=-6.} \\ =9-(-12)+4 ~ & \textcolor{red}{ \text{ Left to right, multiply: } (-6)(2) = -12.} \\ = 9 + 12 + 4 ~ & \textcolor{red}{ \text{ Add the opposite.}} \\ = 25 ~ & \textcolor{red}{ \text{ Add.}} \end{aligned}\nonumber$$

Вправа

Якщо x = −2 і y = −1, оцініть x ³ − y ³.

Відповідь

−7

Приклад 2

Оцінити вираз (a − b) ² Якщо a = 3 і b = −5, при a = 3 і b = −5.

Рішення

Дотримуючись «Поради щодо оцінки алгебраїчних виразів», спочатку замініть усі входження змінних у виразі (a − b) ² відкритими дужками.

$$(a-b)^2 = (()-())^2\nonumber$$

По-друге, замініть кожну змінну на задане значення, а по-третє, дотримуйтесь «Правил, що керівний порядок операцій», щоб оцінити отриманий вираз.

$$\begin{aligned} (a-b)^2 = (( \textcolor{red}{3})-( \textcolor{red}{-5}))^2 ~ & \textcolor{red}{ \text{ Substitute 3 for } a \text{ and } -5 \text{ for } b.} \\ = (3+5)^2 ~ & \textcolor{red}{ \text{ Add the opposite: } (3)-(-5)=3+5} \\ = 8^2 ~ & \textcolor{red}{ \text{ Simplify inside parentheses: } 3+5 = 8} \\ =64 ~ & \textcolor{red}{ \text{ Evaluate exponent: } 8^2 = 64} \end{aligned}\nonumber$$

Вправа

Якщо a = 3 і b = −5, оцініть a ² − b ².

Відповідь

−16

Приклад 3

Оцінити вираз |a|−|b| при a = 5 та b = −7.

Рішення

Дотримуючись «Поради щодо обчислення алгебраїчних виразів», спочатку замініть усі входження змінних у виразі |a|−|b| відкритими дужками.

$$|a| - |b| = |( ~ )| - |( ~ )|\nonumber$$

По-друге, замініть кожну змінну на задане значення, а по-третє, дотримуйтесь «Правил, що керівний порядок операцій», щоб оцінити отриманий вираз.

$$\begin{aligned} |a| - |b| = |( \textcolor{red}{5} )| = |( \textcolor{red}{-7})| ~ & \textcolor{red}{ \text{ Substitute 5 for } a \text{ and } -7 \text{ for } b.} \\ = 5 - 7 ~ & \textcolor{red}{ \text{ Absolute values first: } |(5)| = 5 \text{ and } |(-7)|=7|} \\ =5+(-7) ~ & \textcolor{red}{ \text{ Add the opposites: } 5 - 7 = 5+(-7).} \\ =-2 ~ & \textcolor{red}{ \text{ Add: } 5+(-7)=-2.} \end{aligned}\nonumber$$

Вправа

Якщо a = 5 і b = −7, оцініть 2| a | − 3| b |.

Відповідь

−11

Приклад 4

Оцінити вираз | a − b | при a = 5 і b = −7.

Рішення

Слідуючи «Поради щодо оцінки алгебраїчних виразів», спочатку замініть усі входження змінних у виразі | a − b | відкритими дужками.

$$|a-b| = |(~)-(~)|\nonumber$$

По-друге, замініть кожну змінну на задане значення, а по-третє, дотримуйтесь «Правил, що керівний порядок операцій», щоб оцінити отриманий вираз.

$$\begin{aligned} |a-b| = |( \textcolor{red}{5})-( \textcolor{red}{-7})| ~ & \textcolor{red}{ \text{ Substitute 5 for } a \text{ and } -7 \text{ for } b.} \\ = |5+7| ~ & \textcolor{red}{ \text{ Add the opposite: } 5-(-7)=5+7.} \\ =|12| ~ & \textcolor{red}{ \text{ Add: } 5+7=12.} \\ =12 ~ & \textcolor{red}{ \text{ Take the absolute value: } |12| = 12.} \end{aligned}\nonumber$$

Вправа

Якщо a = 5 і b = −7, оцініть |2 a − 3 b |.

Відповідь

31

Приклад 5

Оцініть вираз

$$\frac{ad-bc}{a+b}\nonumber$$

при a = 5, b = −3, c = 2, а d = −4.

Рішення

Дотримуючись «Поради щодо оцінки алгебраїчних виразів», спочатку замініть усі входження змінних у виразі відкритими дужками.

$$\frac{ad-bc}{a+b} = \frac{(~)(~)-(~)(~)}{(~)+(~)}\nonumber$$

По-друге, замініть кожну змінну на задане значення, а по-третє, дотримуйтесь «Правил, що керівний порядок операцій», щоб оцінити отриманий вираз.

$$\begin{aligned} \frac{ad-bc}{a+b} = \frac{( \textcolor{red}{5}) -( \textcolor{red}{-3}) ( \textcolor{red}{2})}{( \textcolor{red}{5}) + ( \textcolor{red}{-3})} ~ & \textcolor{red}{ \text{ Substitute: } 5 \text{ for } a,~ -3 \text{ for } b,~ 2 \text{ for } c,~ -4 \text{ for } d.} \\ = \frac{-20-(-6)}{2} ~ & \begin{aligned} \textcolor{red}{ \text{ Numerator: } (5)(=4)=-20,~ (-3)(2) = -6.} \\ \textcolor{red}{ \text{ Denominator: } 5+(-3)=2.} \end{aligned} \\ = \frac{-20+6}{2} ~ & \textcolor{red}{ \text{ Numerator: Add the opposite.}} \\ = \frac{-14}{2} ~ & \textcolor{red}{ \text{ Numerator: } -20+6=-14.} \\ = -7 ~ & \textcolor{red}{ \text{Divide.}} \end{aligned}\nonumber$$

Вправа

Якщо a = −7, b = −3, c = −15, 15 і d = −14, оцініть:

$$\frac{a^2+b^2}{c+d}\nonumber$$

Відповідь

−2

приклад 6

На фото нижче - прямокутна призма.

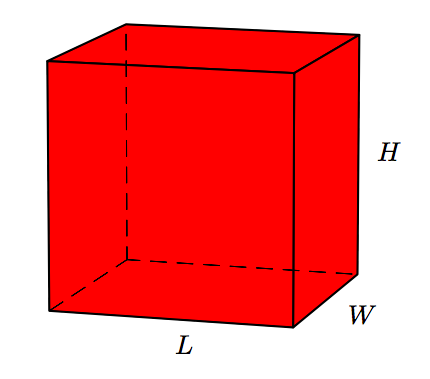
Обсяг прямокутної призми задається за формулою

$$V=LWH,\nonumber$$

де L - довжина, W - ширина, а H - висота прямокутної призми. Знайдіть об'єм прямокутної призми, що має довжину 12 футів, ширину 4 фути та висоту 6 футів.

Рішення

Дотримуючись «Поради щодо оцінки алгебраїчних виразів», спочатку замініть усі випадки L, W та H у формулі

$$V = LWH\nonumber$$

з відкритими дужками.

$$V = (~)(~)(~)\nonumber$$

Далі замініть 12 футів на L, 4 фути для W та 6 футів для H та спростити.

$$\begin{aligned} V = (12 \text{ft})(4 \text{ft})(6 \text{ft}) \\ = 288 \text{ft}^3 \end{aligned}\nonumber$$

Значить, обсяг прямокутної призми становить 288 кубічних футів.

Вправа

Площа поверхні призми, зображеної в цьому прикладі, задається за такою формулою:

$$S = 2(W H + LH + LW) \nonumber$$

Якщо L = 12, W = 4, а H = 6 футів, відповідно, обчисліть площу поверхні.

Відповідь

288 квадратних футів

Вправи

У вправах 1-12 оцініть вираз за заданим значенням x.

1. −3x ² − 6х+ 3 при х = 7

2. 7х ² − 7х+ 1 при х = −8

3. −6x − 6 при x = 3

4. 6x − 1 при х = −10

5. 5х ² + 2х+ 4 при х = −1

6. 4х ² − 9х+ 4 при х = −3

7. −9x − 5 при x = −2

8. −9х + 12 при х = 5

9. 4х ² + 2х+ 6 при х = −6

10. −3х ² + 7х+ 4 при х = −7

11. 12х + 10 при х = −12

12. −6х + 7 при х = 11

---

У вправах 13-28 оцініть вираз при заданих значеннях x і y.

13. |x|−|y| при x = −5 та y = 4

14. |x|−|y| при x = −1 та y = −2

15. −5х ² + 2у ² при х = 4 і у = 2

16. −5x ² − 4y ² при x = −2 та y = −5

17. |x|−|y| при х = 0 і у = 2

18. |x|−|y| при x = −2 та y = 0

19. |x − y| при x = 4 і y = 5

20. |x − y| при x = −1 і y = −4

21. 5x ² − 4xy + 3y ² при х = 1 і y = −4

22. 3х ² + 5xy + 3у ² при х = 2 і у = −1

23. |x − y| при x = 4 і y = 4

24. |x − y| при x = 3 і y = −5

25. −5x ² − 3xy + 5y ² при x = −1 і y = −2

26. 3x ² − 2xy − 5y ² при х = 2 і y = 5

27. 5х ² + 4у ² при х = −2 і у = −2

28. −4x ² + 2y ² при х = 4 і y = −5

---

У вправах 29-40 оцініть вираз при заданому значенні x.

29. $\frac{9+9x}{−x}$при x = −3

30. $\frac{9 − 2x}{−x}$при x = −1

31. $\frac{−8x + 9}{−9 + x}$при х = 10

32. $\frac{2x + 4}{1 + x}$при х = 0

33. $\frac{−4+9x}{7x}$при х = 2

34. $\frac{−1 − 9x}{x}$при x = −1

35. $\frac{−12 − 7x}{x}$при x = −1

36. $\frac{12 + 11x}{3x}$при x = −6

37. $\frac{6x − 10}{5}$+ х при x = −6

38. $\frac{11x + 11}{−4}$+ х при х = 5

39. $\frac{10x + 11}{5}$+ х при x = −4

40. $\frac{6x + 12}{−3}$+ х при х = 2

---

41. Формула

$$d=16t^2\nonumber$$

дає відстань (у футах), яку об'єкт падає з відпочинку з точки зору часу t, який минув з моменту його звільнення. Знайдіть відстань d (у футах), що об'єкт потрапляє за t = 4 секунди.

42. Формула

$$d = 16t^2\nonumber$$

дає відстань (у футах), яку об'єкт падає з відпочинку з точки зору часу t, який минув з моменту його звільнення. Знайдіть відстань d (у футах), що об'єкт потрапляє за t = 24 секунди.

43. Формула

$$C = \frac{5(F − 32)}{9}\nonumber$$

дає температуру Цельсія C через температуру Фаренгейта F Використовуйте формулу, щоб знайти температуру Цельсія (◦ C), якщо температура Фаренгейта дорівнює F = 230◦ F.

44. Формула

$$C = \frac{5(F − 32)}{9}\nonumber$$

дає температуру Цельсія C через температуру Фаренгейта F Використовуйте формулу, щоб знайти температуру Цельсія (^◦ C), якщо температура Фаренгейта дорівнює F = 95 ^◦ F.

45. Шкала температури Кельвіна використовується в хімії і фізиці. Абсолютний нуль виникає при 0 ^◦ К, температурі, при якій молекули мають нульову кінетичну енергію. Вода замерзає при 273 ^◦ К і кипить при K = 373 ^◦ K. Для зміни температури Кельвіна на температуру Фаренгейта використовуємо формулу

$$F = \frac{9(K − 273)}{5} + 32.\nonumber$$

Використовуйте формулу, щоб змінити 28 ^◦ K на Фаренгейт.

46. Шкала температури Кельвіна використовується в хімії і фізиці. Абсолютний нуль виникає при 0 ^◦ К, температурі, при якій молекули мають нульову кінетичну енергію. Вода замерзає при 273 ^◦ К і кипить при K = 373 ^◦ K. Для зміни температури Кельвіна на температуру Фаренгейта використовуємо формулу

$$F = \frac{9(K − 273)}{5} + 32.\nonumber$$

Використовуйте формулу, щоб змінити 248 ^◦ K на Фаренгейт.

47. Куля кидається вертикально вгору. Його швидкість t секунд після її звільнення задається за формулою

$$v = v0 − gt,\nonumber$$

де v ₀ - його початкова швидкість, g - прискорення за рахунок сили тяжіння, а v - швидкість кулі в момент t. прискорення за рахунок гравітації становить g = 32 фути в секунду в секунду. Якщо початкова швидкість м'яча дорівнює v ₀ = 272 футів в секунду, знайдіть швидкість м'яча після t = 6 секунд.

48. Куля кидається вертикально вгору. Його швидкість t секунд після її звільнення задається за формулою

$$v = v_0 − gt,\nonumber$$

де v ₀ - його початкова швидкість, g - прискорення за рахунок сили тяжіння, а v - швидкість кулі в момент t. прискорення за рахунок гравітації становить g = 32 фути в секунду в секунду. Якщо початкова швидкість м'яча дорівнює v ₀ = 470 футів в секунду, знайдіть швидкість м'яча після t = 4 секунди.

---

49. Парні числа. Оцініть вираз 2n для наступних значень:

i) п = 1

ii) п = 2

iii) п = 3

iv) п = −4

v) п = −5

vi) Чи завжди результат парне число? Поясніть.

50. Непарні числа. Оцініть вираз 2n + 1 для наступних значень:

i) п = 1

ii) п = 2

iii) п = 3

iv) п = −4

v) п = −5

vi) Чи завжди результат непарне число? Поясніть.

---

Відповіді

1. −186

3. −24

5. 7

7. 13

9. 138

11. −134

13. 1

15. −72

17. −2

19. 1

21. 69

23. 0

25. 9

27. 36

29. −6

31. −71

33. 1

35. 5

37. 46

39. −29

41. 256 футів

43. 110 градусів

45. −409 ^◦ F

47. 80 футів в секунду

49.

i) 2

ii) 4

iii) 6

iv) −8

v) −10

vi) Так, результат завжди буде парним числом, тому що 2 завжди буде множником продукту 2n.