2.2: Додавання цілих чисел
- Page ID
- 57333
Як і наша робота з цілими числами, додавання цілих чисел найкраще пояснити за допомогою діаграм числових ліній. Однак, перш ніж ми почнемо, давайте знайдемо хвилинку, щоб обговорити поняття вектора.
Вектори
Вектор - це математичний об'єкт, який має дві якості імпорту: (1) величина або довжина та (2) напрямок.
Вектори є фундаментальним інструментом вирішення проблем в математиці, науці та інженерії. У фізиці вектори використовуються для представлення сил, положення, швидкості та прискорення, тоді як інженери використовують вектори для представлення як внутрішніх, так і зовнішніх сил на спорудах, таких як мости та будівлі. У цьому курсі, і в цьому конкретному розділі, ми зосередимося на використанні векторів, щоб допомогти пояснити додавання цілих чисел.
Вектори на числовому рядку
Розглянемо числовий рядок на малюнку\(\PageIndex{1}\).
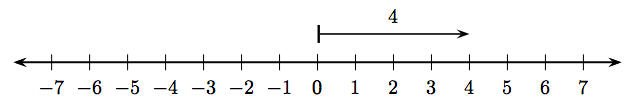
Над лінією ми намалювали вектор з хвостом, починаючи з цілого числа 0 і стрілки закінчуючи цілим числом 4. Є дві важливі речі, які слід зазначити щодо цього вектора:
- Величина (довжина) вектора на малюнку\(\PageIndex{1}\) дорівнює чотирьом.
- Вектор на малюнку\(\PageIndex{1}\) вказує праворуч.
Погодьмося, що вектор на малюнку\(\PageIndex{1}\) являє собою позитивну четвірку. Не важливо, щоб вектор починався з початку. Розглянемо, наприклад, вектор, зображений на малюнку\(\PageIndex{2}\).

Знову ж таки, слід зробити два важливих спостереження:
- Величина (довжина) вектора на малюнку\(\PageIndex{2}\) дорівнює чотирьом.
- Вектор на малюнку\(\PageIndex{2}\) вказує праворуч.
Сподіваюся, у вас є ідея. Будь-який вектор, який має довжину 4 і вказує праворуч, буде представляти позитивну четвірку, незалежно від його початкової або кінцевої точки. І навпаки, розглянемо вектор на малюнку\(\PageIndex{3}\), який починається з цілого числа 4 і закінчується цілим числом −3.
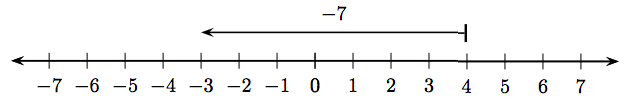
Два спостереження:
- Величина (довжина) вектора на малюнку\(\PageIndex{3}\) дорівнює семи.
- Вектор на малюнку\(\PageIndex{3}\) вказує ліворуч.
Погодьмося, що вектор на малюнку\(\PageIndex{3}\) представляє негативну сімку. Ми могли б вибрати різні початкові та кінцеві точки для нашого вектора, але якщо вектор має довжину сім і вказує ліворуч, він представляє ціле число −7.
Важливе спостереження
Вектор, що вказує вправо, являє собою додатне число. Вектор, що вказує ліворуч, являє собою від'ємне число.
Величина і абсолютне значення
На малюнку\(\PageIndex{1}\) та\(\PageIndex{2}\) малюнку зображені вектори представляють ціле натуральне чотири. Зверніть увагу, що абсолютне значення чотирьох дорівнює чотирьом; тобто |4| = 4. Зауважте також, що це абсолютне значення є величиною або довжиною векторів, що представляють ціле число позитивних чотирьох на рисунку\(\PageIndex{1}\) та рисунку\(\PageIndex{2}\).
На\(\PageIndex{3}\) малюнку зображений вектор представляє ціле число −7. Зауважте, що | − 7| = 7. Це показує, що абсолютне значення представляє величину або довжину вектора, що представляє −7.
Величина і абсолютне значення
Якщо a є цілим числом, то | a | дає величину або довжину вектора, що представляє ціле число a.
Додавання цілих чисел з подібними знаками
Оскільки позитивні цілі числа також цілі числа, ми вже бачили, як додати до них у розділі 1.2.
Приклад 1
Знайти суму 3 + 4.
Рішення
Щоб скласти натуральні числа 3 і 4, дійте наступним чином.
- Почніть з цілого числа 0, потім намалюйте вектор довжиною 3 одиниці, що вказують праворуч, як показано на малюнку\(\PageIndex{4}\). Ця стрілка має величину (довжину) три і являє собою додатне ціле число 3.
- Намалюйте другий вектор довжиною чотири, який вказує праворуч, починаючи з кінця першого вектора, що представляє додатне ціле число 3. Ця стрілка має величину (довжину) чотири і являє собою додатне ціле число 4.
- Сума натуральних чисел 3 і 4 може бути представлена вектором, який починається з цілого числа 0 і закінчується натуральним числом 7. Однак ми вважаємо за краще позначити цю суму на числовому рядку як суцільну крапку в додатному цілому числі 7. Це ціле число являє собою суму натуральних чисел 3 і 4.
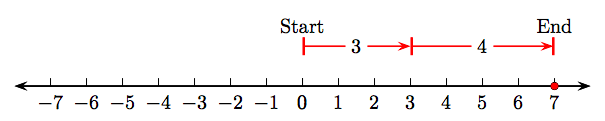
Таким чином, 3 + 4 = 7
Вправа
Використовуйте діаграму числової лінії, щоб показати суму 5 + 7.
- Відповідь
-
12
Негативні цілі числа додаються аналогічним чином.
Приклад 2
Знайти суму −3+ (−4).
Рішення
Щоб додати від'ємні цілі числа −3 та −4, виконайте такі дії.
- Почніть з цілого числа 0, потім намалюйте вектор довжиною 3 одиниці, що вказують ліворуч, як показано на малюнку\(\PageIndex{5}\). Ця стрілка має величину (довжину) три і являє собою від'ємне ціле число −3.
- Намалюйте другий вектор довжиною чотири, який вказує ліворуч, починаючи з кінця першого вектора, що представляє від'ємне ціле число −3. Ця стрілка має величину (довжину) чотири і являє собою від'ємне ціле число −4.
- Суму від'ємних цілих чисел −3 та −4 можна представити вектором, який починається з цілого числа 0 і закінчується від'ємним цілим числом −7. Однак ми вважаємо за краще позначати цю суму на числовому рядку як суцільну крапку з від'ємним цілим числом −7. Це ціле число являє собою суму від'ємних цілих чисел −3 та −4.

Таким чином, −3+ (−4) = −7.
Малювання на фізичній інтуїції. Уявіть, що ви «ходите по цифровій лінії» на малюнку\(\PageIndex{5}\). Ви починаєте з початку (нуль) і робите 3 кроки вліво. Далі ви пройдете ще чотири кроки ліворуч, приземляючись на число −7
Вправа
Використовуйте діаграму числових ліній, щоб показати суму −7+ (−3).
- Відповідь
-
−10
Не дивно, що процедура, яка використовується для додавання двох від'ємних цілих чисел, складається з двох кроків.
Додавання двох від'ємних цілих чисел
Щоб додати два від'ємних цілих числа, дійте наступним чином:
- Додайте величини цілих чисел.
- Префікс загального негативного знака
Приклад 3
Знайти суми: (a) −4+ (−5), (b) −12 + (−9) та (c) −2+ (−16).
Рішення
Ми розглянемо три окремі, але еквівалентні підходи, про які йшлося в розповіді вище.
а) Схема числової лінії
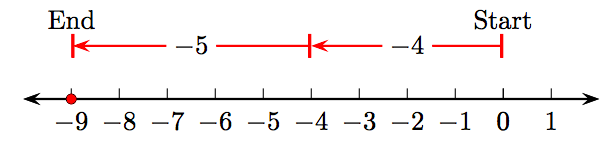
показує, що (−4) + (−5) = −9.
б) Спираючись на фізичну інтуїцію, починайте з нуля, пройдіть 12 одиниць вліво, потім ще 9 одиниць вліво. Ви повинні знайти собі 21 одиницю зліва від початку (нуль). Отже, −12 + (−9) = −21.
c) Дотримуючись описаного вище алгоритму в розділі «Додавання двох від'ємних цілих чисел», спочатку додайте величини −2 та −16; тобто 2+16 = 18. Тепер приставка загальний знак. Отже, −2+ (−16) = −18.
Вправа
Знайти суму: −5+ (−9).
- Відповідь
-
−14
Додавання цілих чисел з несхожими знаками
Додавання цілих чисел з несхожими знаками не складніше, ніж додавання цілих чисел з подібними знаками.
Приклад 4
Знайти суму −8 + 4.
Рішення
Щоб знайти суму −8 + 4, дійте наступним чином:
- Почніть з цілого числа 0, потім намалюйте вектор довжиною вісім одиниць, що вказують ліворуч, як показано на малюнку\(\PageIndex{6}\). Ця стрілка має величину (довжину) вісім і являє собою від'ємне ціле число −8.
- Намалюйте другий вектор довжиною чотири, який вказує праворуч, починаючи з кінця першого вектора, що представляє від'ємне ціле число −8. Ця стрілка (також показана на малюнку\(\PageIndex{6}\)) має величину (довжину) чотири і являє собою натуральне число 4.
- Суму від'ємних цілих чисел −8 і 4 можна представити вектором, який починається з цілого числа 0 і закінчується від'ємним цілим числом −4. Однак ми вважаємо за краще позначати цю суму на числовому рядку як суцільну крапку з від'ємним цілим числом −4. Це ціле число являє собою суму цілих чисел −8 та 4.
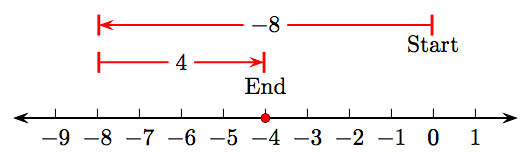
Таким чином, −8+4= −4.
Малювання на фізичній інтуїції. Уявіть, що ви «ходите по цифровому рядку на малюнку\(\PageIndex{6}\). Ви починаєте з початку (нуль) і йдете вісім кроків вліво. Далі оберніться і пройдіться чотирма кроками вправо, приземляючись на число −4.
Вправа
Використовуйте діаграму числових ліній, щоб показати суму −9 + 2.
- Відповідь
-
−7
Зауважте, що додавання цілих чисел з несхожими знаками є віднімним процесом. Це пов'язано з переворотом напрямку, який відчувається при малюванні Рисунок\(\PageIndex{6}\) у прикладі 4.
Додавання двох цілих чисел з несхожими знаками
Щоб скласти два цілих числа з несхожими знаками, дійте наступним чином:
- Відніміть меншу величину від більшої величини.
- Префікс знака числа з більшою величиною.
Наприклад, щоб знайти суму −8 + 4 з прикладу 4, зауважимо, що цілі числа −8 та 4 мають значення 8 та 4 відповідно. Потім ми застосуємо процес, описаний у розділі «Додавання двох цілих чисел з несхожими знаками».
- Відніміть меншу величину від більшої величини; тобто 8 − 4 = 4.
- Префікс знака числа з більшою величиною. Оскільки −8 має більшу величину, а його знак негативний, ми приставимо негативний знак до різниці величин. Таким чином, −8+4= −4.
Приклад 5
Знайти суми: (a) 5+ (−8), (b) −12+ 16 та (c) −117+115.
Рішення
Ми розглянемо три окремі, але еквівалентні підходи, про які йшлося в розповіді вище.
а) Схема числової лінії
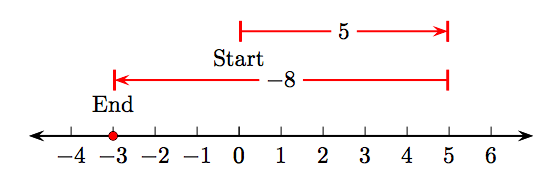
показує, що 5 + (−8) = −3.
б) Спираючись на фізичну інтуїцію, починайте з нуля, пройдіть 12 одиниць вліво, потім оберніться і пройдіть 16 одиниць вправо. Ви повинні знайти собі 4 одиниці праворуч від початку (нуль). Отже, −12 + 16 = 4.
c) Дотримуючись алгоритму «Додавання двох цілих чисел із знаками відмінності», відніміть меншу величину від більшої величини, таким чином 117−115 = 2. Оскільки −117 має більшу величину і його знак негативний, ми ставимо від'ємний знак до різниці величин. Таким чином, −117 + 115 = −2.
Вправа
Використовуйте діаграму числових ліній, щоб показати суму 5 + (−11).
- Відповідь
-
−6
Властивості додавання цілих чисел
Вам буде приємно дізнатися, що властивості додавання для цілих чисел також застосовуються до додавання цілих чисел.
Комутативна властивість додавання
Нехай a і b представляють два цілих числа. Потім,
\[a + b = b + a.\nonumber \]
Приклад 6
Показати, що 5 + (−7) = −7 + 5.
Рішення
Схема числового рядка
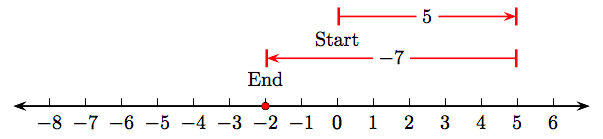
показує, що 5 + (−7) = −2. З іншого боку, схема числової лінії
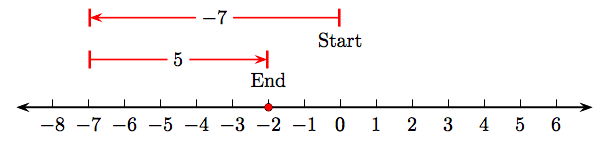
показує, що −7+5= −2. Тому 5 + (−7) = −7 + 5.
Вправа
Скористайтеся діаграмою числових ліній, щоб показати, що −8+ 6 збігається з 6 + (−8).
Додавання цілих чисел також асоціативно.
Асоціативна властивість додавання
Нехай a, b і c представляють цілі числа. Потім,
\[(a + b) + c = a + (b + c)\nonumber \].
Приклад 7
Показати, що (−9 + 6) + 2 = −9 + (6 + 2).
Рішення
Ліворуч символи групування вимагають, щоб спочатку додати −9 та 6. Таким чином,
\[ \begin{aligned} (−9 + 6) + 2 & = −3+2 \\ ~ & = −1. \end{aligned}\nonumber \]
Праворуч символи групування вимагають, щоб ми спочатку додали 6 і 2. Таким чином,
\[ \begin{aligned} −9 + (6 + 2) & = −9+8 \\ ~ & = −1. \end{aligned}\nonumber \]
Обидві сторони спрощують до −1. Тому (−9 + 6) + 2 = −9 + (6 + 2).
Вправа
Показати, що вираз (−8 + 5) + 3 збігається з −8 + (5 + 3) шляхом спрощення кожного з двох виразів незалежно.
Властивість адитивної ідентичності
Ціле нуль називається адитивним тотожністю. Якщо a - будь-яке ціле число, то
а +0= а і 0 + а = а.
Так, наприклад, −8+0= −8 і 0 + (−113) = −113.
Нарешті, кожне ціле число має унікальну протилежність, звану його адитивною оберненою.
Адитивна зворотна властивість
Дозвольте a представляти будь-яке ціле число. Тоді існує єдине ціле число − a, яке називається протилежним або додатковим оберненим a, таке, що
a + (− a) = 0 і − a + a = 0.
Приклад 8
Показати, що 5 + (−5) = 0.
Рішення
Схема числового рядка
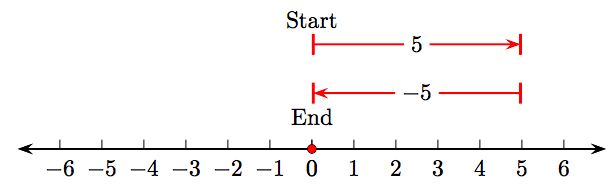
чітко видно, що 5 + (−5) = 0.
Вправа
Використовуйте діаграму числової лінії, щоб показати, що 9 + (−9) = 0.
Важливе спостереження
Ми використали кілька еквівалентних фраз, щоб вимовляти ціле число − a. Ми використовували «протилежність a», «негативний a» і «добавку, обернену a». Всі є рівнозначними вимовами.
Групування за ефективністю
Порядок операцій вимагає, щоб ми виконували всі доповнення в міру їх виникнення, працюючи зліва направо.
Приклад 9
Спростити −7+8+ (−9) + 12.
Рішення
Виконуємо додавання в міру їх виникнення, працюючи зліва направо.
\[ \begin{aligned} =7 + 8 + (-9) +12 = 1 + (-9) +12 ~ & \textcolor{red}{ \text{ Working left to right, } -7 + 8 = 1.} \\ = -8 + 12 ~ & \textcolor{red}{ \text{ Working left to right, } 1 + (-9_ = -8.} \\ =4 ~ & \textcolor{red}{ ~ -8 + 12 = 4} \end{aligned}\nonumber \]
Таким чином, −7+8+ (−9) + 12 = 4.
Вправа
Спрощення: −8+9+ (−4) + 2.
- Відповідь
-
−1
Комутативна властивість додавання говорить нам про те, що зміна порядку додавання не змінює відповіді. Асоціативне властивість додавання говорить нам про те, що на суму не впливає перегрупування. Давайте знову попрацюємо Приклад 9, спочатку групуючи позитивні та негативні числа разом.
приклад 10
Спростити −7+8+ (−9) + 12.
Рішення
Комутативні та асоціативні властивості дозволяють змінювати порядок додавання і перегрупування.
\[ \begin{aligned} -7 + 8 + (-9) + 12 = -7 + (-9) + 8 + 12 ~ & \textcolor{red}{ \text{ Use the commutative property to change the order.}} \\ = [-7+(-9)] + [8+12] ~ & \textcolor{red}{ \text{ Use the associative property to regroup.}} \\ =-16 + 20 ~ & \textcolor{red}{ \text{ Add the negatives. Add the positives.}} \\ =4 ~ & \textcolor{red}{ \text{ One final addition.}} \end{aligned}\nonumber \]
Таким чином, −7+8+ (−9) + 12 = 4.
Вправа
Спрощення: −11 + 7 + (−12) + 3.
- Відповідь
-
−13
На перший погляд, здається, немає ніякої переваги у використанні техніки в прикладі 10 над технікою, яка використовується в прикладі 9. Однак техніка в прикладі 10 набагато швидша на практиці, особливо якщо ви усунете деякі пояснювальні кроки.
Ефективне групування
Коли вас попросять знайти суму цілих чисел, найефективніше спочатку скласти всі натуральні числа, потім додати негативи, а потім додати результати.
Приклад 11
Спростити −7+8+ (−9) + 12.
Рішення
Додайте спочатку натуральні числа, потім негативи, потім додайте результати.
\[ \begin{aligned} -7 + 8 + (-9) +12 = 20 + (-16) ~ & \textcolor{red}{ \text{ Add the positives: } 8 + 12 = 20.} \\ ~ & \textcolor{red}{ \text{ Add the negatives: } -7 + (-9) = -16.} \\ =4 ~ & \textcolor{red}{ \text{ Add the results: } 20 + (-16) = 4.} \end{aligned}\nonumber \]
Таким чином, −7+8+ (−9) + 12 = 4.
Вправа
Спрощення: −11 + 3 + (−2) + 7.
- Відповідь
-
−7
Використання правильних позначень
Ніколи не пишіть +−! Тобто позначення
9 +−4 та − 8 +−6
не слід використовувати. Замість цього використовуйте символи групування наступним чином:
9+ (−4) та −8+ (−6)
Вправи
У вправах 1-12, яке ціле число представлено заданим вектором?
1.
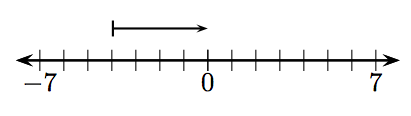
2.
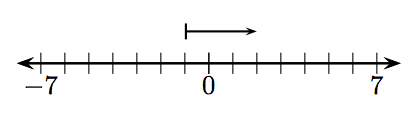
3.
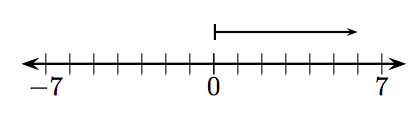
4.
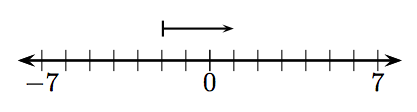
5.
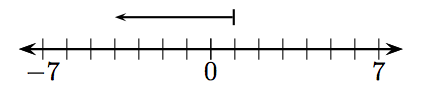
6.
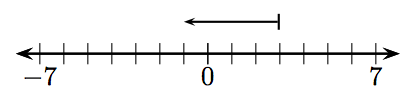
7.
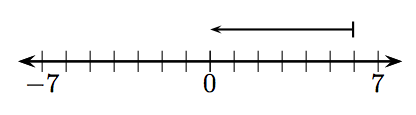
8.
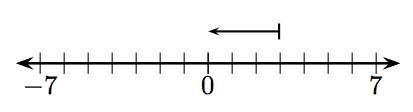
9.
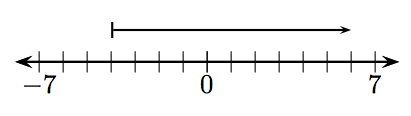
10.
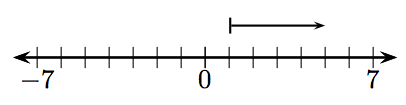
11.
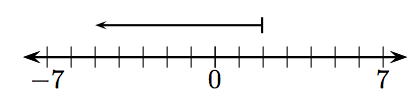
12.
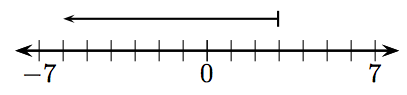
У вправах 13-36 знайдіть суму заданих цілих чисел.
13. −15 + 1
14. −1 + 18
15. 18 + (−10)
16. 2+ (−19)
17. −10 + (−12)
18. −1+ (−7)
19. 5 + 10
20. 1 + 12
21. 2+5
22. 14 + 1
23. 19 + (−15)
24. 20 + (−17)
25. −2+ (−7)
26. −14 + (−6)
27. −6 + 16
28. −2 + 14
29. −11 + (−6)
30. −7+ (−8)
31. 14 + (−9)
32. 5+ (−15)
33. 10 + 11
34. 14 + 11
35. −13 + 1
36. −8+2
У Вправах 37-52 викладіть властивість складання, зображеного заданою ідентичністю.
37. −1 + (3 + (−8)) = (−1 + 3) + (−8)
38. −4 + (6 + (−5)) = (−4 + 6) + (−5)
39. 7+ (−7) = 0
40. 14 + (−14) = 0
41. 15 + (−18) = −18 + 15
42. 14 + (−8) = −8 + 14
43. −15 + 0 = −15
44. −11 + 0 = −11
45. −7 + (1 + (−6)) = (−7 + 1) + (−6)
46. −4 + (8 + (−1)) = (−4 + 8) + (−1)
47. 17 + (−2) = −2 + 17
48. 5+ (−13) = −13 + 5
49. −4+0= −4
50. −7+0= −7
51. 19 + (−19) = 0
52. 5+ (−5) = 0
У вправах 53-64 вкажіть адитивну обернену заданого цілого числа.
53. 18
54. 10
55. 12
56. 15
57. −16
58. −4
59. 11
60. 13
61. −15
62. −19
63. −18
64. −9
У вправах 65-80 знайдіть суму заданих цілих чисел.
65. 6+ (−1) + 3 + (−4)
66. 6+ (−3) + 2 + (−7)
67. 15 + (−1) + 2
68. 11 + (−16) +16
69. −17 + 12 + 3
70. −5+ (−3) + 2
71. 7 + 20 + 19
72. 14 + (−14) + (−20)
73. 4+ (−8) + 2 + (−5)
74. 6+ (−3) + 7 + (−2)
75. 7+ (−8) + 2 + (−1)
76. 8+ (−9) + 5 + (−3)
77. 9+ (−3) + 4 + (−1)
78. 1+ (−9) + 7 + (−6)
79. 9 + 10 + 2
80. −6 + 15 + (−18)
81. Банківський рахунок. Джеррі відкрив новий банківський рахунок, здавши чек на 215 доларів. Потім він зробив кілька вилучень $40, $75 і $20, перш ніж здати ще один чек на $185. Скільки зараз на рахунку Джеррі?
82. Мертве море тоне. Через рух тектонічних плит Мертве море тоне близько 1 метра щороку. Якщо зараз вона становить −418 метрів, якою буде висота Мертвого моря через 5 років? Напишіть вираз, що моделює цю ситуацію, і обчислити результат.
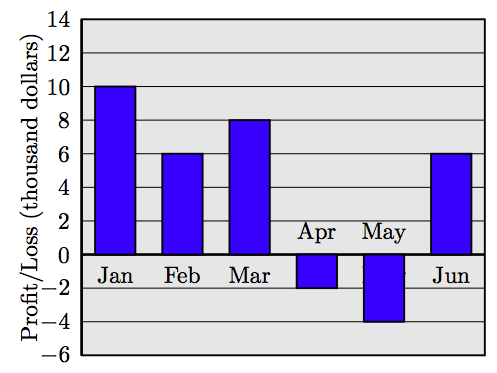
83. Прибуток і збиток. Прибутки і збитки за перші шість місяців фінансового року для малого бізнесу показані на наступній гістограмі. Підсумуйте прибуток і збитки з кожного місяця. Чи був чистий прибуток або збиток за шість місяців? Скільки?
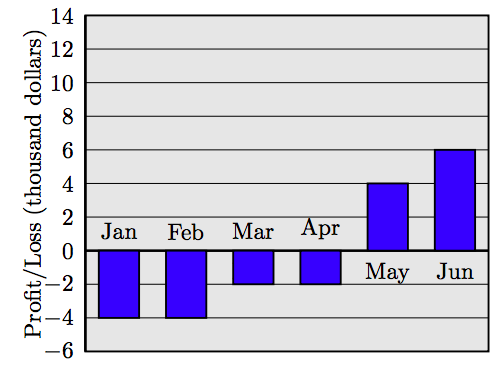
84. Прибуток і збиток. Прибутки і збитки за перші шість місяців фінансового року для малого бізнесу показані на наступній гістограмі. Підсумуйте прибуток і збитки з кожного місяця. Чи був чистий прибуток або збиток за шість місяців? Скільки?
Відповіді
1. 4
3. 6
5. −5
7. −6
9. 10
11. −7
13. −14
15. 8
17. −22
19. 15
21. 7
23. 4
25. −9
27. 10
29. −17
31. 5
33. 21
35. −12
37. Асоціативна властивість додавання
39. Адитивна зворотна властивість
41. Комутативна властивість додавання
43. Властивість адитивної ідентичності
45. Асоціативна властивість додавання
47. Комутативна властивість додавання
49. Властивість адитивної ідентичності
51. Адитивна зворотна властивість
53. −18
55. −12
57. 16
59. −11
61. 15
63. 18
65. 4
67. 16
69. −2
71. 46
73. −7
75. 0
77. 9
79. 21
81. 265 доларів
83. Чистий прибуток: $24,000
