2.6: Інтеграційні фактори
- Page ID
- 62359
У розділі 2.5 ми побачили, що якщо\(M\)\(N\),\(M_y\) і\(N_x\) є безперервними і\(M_y=N_x\) на відкритому прямокутнику,\(R\) то
\[\label{eq:2.6.1} M(x,y)\,dx+N(x,y)\,dy=0\]
точно на\(R\). Іноді рівняння, яке не є точним, можна зробити точним, помноживши його на відповідну функцію. Наприклад,
\[\label{eq:2.6.2} (3x+2y^2)\,dx+2xy\,dy=0\]
не є точним, оскільки\(M_y(x,y)=4y\ne N_x(x,y)=2y\) в рівнянні\ ref {eq:2.6.2}. Однак множення рівняння\ ref {eq:2.6.2} на\(x\) врожайність
\[\label{eq:2.6.3} (3x^2+2xy^2)\,dx+2x^2y\,dy=0,\]
що є точним, оскільки\(M_y(x,y)=N_x(x,y)=4xy\) в рівнянні\ ref {eq:2.6.3}. Розв'язування рівняння\ ref {eq:2.6.3} за процедурою, наведеною в розділі 2.5, дає неявне розв'язання
\[x^3+x^2y^2=c.\nonumber \]
Функція\(\mu=\mu(x,y)\) є інтеграційним коефіцієнтом для Equation\ ref {eq:2.6.1}, якщо\[\label{eq:2.6.4} \mu(x,y)M (x,y)\,dx+\mu(x,y)N (x,y)\,dy=0\] є точним. Якщо ми знаємо інтеграційний коефіцієнт\(\mu\) для Equation\ ref {eq:2.6.1}, ми можемо вирішити точне рівняння Equation\ ref {eq:2.6.4} методом Розділу 2.5. Було б непогано, якби ми могли сказати, що Equation\ ref {eq:2.6.1} і Equation\ ref {eq:2.6.4} завжди мають однакові рішення, але це не так. Наприклад,\(y=y(x)\) розв'язок Equation\ ref {eq:2.6.4} такий, що\(\mu(x,y(x))=0\) на деякому інтервалі\(a<x<b\) може не бути розв'язком\ ref {eq:2.6.1} (Вправа 2.6.1)
Знаходження інтеграційних факторів
Застосовуючи теорему 2.5.2 (з\(M\) і\(N\) замінено на\(\mu M\) і\(\mu N\)), ми бачимо, що рівняння\ ref {eq:2.6.4} є точним для відкритого прямокутника\(\mu M\),\(R\) якщо\(\mu N\),,\((\mu M)_y\), і\((\mu N)_x\) є неперервними і\[{\partial\over\partial y}(\mu M)={\partial\over\partial x} (\mu N) \quad \text{or, equivalently,} \quad \mu_yM+\mu M_y=\mu_xN+\mu N_x\nonumber \] на\(R\). Краще переписати останнє рівняння, як\[\label{eq:2.6.5} \mu(M_y-N_x)=\mu_xN-\mu_yM,\] яке зводиться до відомого результату для точних рівнянь; тобто якщо\(M_y=N_x\) тоді Equation\ ref {eq:2.6.5} має значення\(\mu=1\), тому Equation\ ref {eq:2.6.1} є точним.
Ви можете подумати, що Equation\ ref {eq:2.6.5} мало значення, оскільки воно включає часткові похідні невідомого інтегруючого фактора\(\mu\), і ми не вивчали методи розв'язання таких рівнянь. Однак тепер ми покажемо, що Equation\ ref {eq:2.6.5} корисно, якщо ми обмежуємо наш пошук інтеграційними факторами, які є добутком функції\(x\) та функції\(y\); тобто\(\mu(x,y)=P(x)Q(y)\). Ми не говоримо, що кожне рівняння\(M\,dx+N\,dy=0\) має інтеграційний коефіцієнт такої форми; скоріше, ми говоримо, що деякі рівняння мають такі інтегруючі фактори.Ми розробимо спосіб визначити, чи має дане рівняння такий інтегруючий коефіцієнт, і метод знаходження інтегруючого фактора в даному випадку.
Якщо\(\mu(x,y)=P(x)Q(y)\), то\(\mu_x(x,y)=P'(x)Q(y)\) і\(\mu_y(x,y)=P(x)Q'(y)\), так рівняння\ ref {eq:2.6.5} стає
\[\label{eq:2.6.6} P(x)Q(y)(M_y-N_x)=P'(x)Q(y)N-P(x)Q'(y)M,\]або, розділивши наскрізь на\(P(x)Q(y)\),
\[\label{eq:2.6.7} M_y-N_x={P'(x)\over P(x)}N-{Q'(y)\over Q(y)}M.\]Тепер нехай\[p(x)={P'(x)\over P(x)} \quad \text{and} \quad q(y)={Q'(y)\over Q(y)},\nonumber \] так рівняння\ ref {eq:2.6.7} стає
\[\label{eq:2.6.8} M_y-N_x=p(x)N-q(y)M.\]
Ми отримали Equation\ ref {eq:2.6.8}, припускаючи, що\(M\,dx+N\,dy=0\) має інтегруючий коефіцієнт\(\mu(x,y)=P(x)Q(y)\). Однак тепер ми можемо по-різному переглядати Equation\ ref {eq:2.6.7}: Якщо є функції\(p=p(x)\) і\(q=q(y)\) які задовольняють Equation\ ref {eq:2.6.8} і ми визначаємо
\[\label{eq:2.6.9} P(x)=\pm e^{\int p(x)\,dx}\quad \text{and} \quad Q(y)=\pm e^{\int q(y)\,dy},\]
потім перехід кроків, що призвели від Equation\ ref {eq:2.6.6} до Equation\ ref {eq:2.6.8} показує, що\(\mu(x,y)=P(x)Q(y)\) це інтеграційний коефіцієнт для\(M\,dx+N\,dy=0\). Використовуючи цей результат, ми приймаємо константи інтеграції в Equation\ ref {eq:2.6.9} нульовими і вибираємо знаки зручно, щоб коефіцієнт інтегрування мав найпростішу форму.
Не існує простого загального методу для з'ясування того, чи існують функції\(p=p(x)\) та\(q=q(y)\) задовольняє Equation\ ref {eq:2.6.8}. Однак наступна теорема дає прості достатні умови для того, щоб дане рівняння мало інтегруючий коефіцієнт, який залежить тільки від однієї з незалежних змінних\(x\) і\(y\), і для знаходження інтегруючого коефіцієнта в даному випадку.
\(N_x\)Дозволяти\(M,\)\(N,\)\(M_y,\) і бути безперервним на відкритому\(R.\) прямокутнику Тоді:
(а) Якщо\((M_y-N_x)/N\) незалежний від\(y\) на,\(R\) і ми визначаємо,\[p(x)={M_y-N_x\over N}\nonumber \] то\[\label{eq:2.6.10} \mu(x)=\pm e^{\int p(x)\,dx}\] є інтеграційним фактором для\[\label{eq:2.6.11} M(x,y)\,dx+N(x,y)\,dy=0\] на\(R.\)
(b) Якщо\((N_x-M_y)/M\) незалежний від\(x\) on\(R\) і ми визначаємо,\[q(y)={N_x-M_y\over M},\nonumber \] то\[\label{eq:2.6.12} \mu(y)=\pm e^{\int q(y)\,dy}\] є інтеграційним коефіцієнтом для Рівняння\ ref {eq:2.6.11} на\(R.\)
- Доказ
-
(a) Якщо\((M_y-N_x)/N\) не залежить від\(y\), то рівняння\ ref {eq:2.6.8} утримується з\(p=(M_y-N_x)/N\) і\(q\equiv0\). \[P(x)=\pm e^{\int p(x)\,dx}\quad\text{ and}\quad Q(y)=\pm e^{\int q(y)\,dy}=\pm e^0=\pm1,\nonumber \]Тому рівняння\ ref {eq:2.6.10} є інтегруючим коефіцієнтом для рівняння\ ref {eq:2.6.11} на\(R\).
(b) Якщо\((N_x-M_y)/M\) незалежний від\(x\) то eqref eq:2.6.8 тримає з і\(p\equiv0\),\(q=(N_x-M_y)/M\) і подібний аргумент показує, що Equaration\ ref {eq:2.6.12} є інтеграційним коефіцієнтом для рівняння\ ref {eq:2.6.11} on.\(R\)
Наступні два приклади показують, як застосовувати теорему Template:index.
Знайдіть інтегруючий коефіцієнт для рівняння\[\label{eq:2.6.13} (2xy^3-2x^3y^3-4xy^2+2x)\,dx+(3x^2y^2+4y)\,dy=0\] і вирішіть рівняння.
Рішення
У рівнянні\ ref {eq:2.6.13}\[M=2xy^3-2x^3y^3-4xy^2+2x,\ N=3x^2y^2+4y,\nonumber \] і\[M_y-N_x=(6xy^2-6x^3y^2-8xy)-6xy^2=-6x^3y^2-8xy,\nonumber \] тому Рівняння\ ref {eq:2.6.13} не є точним. Однак,\[{M_y-N_x\over N}=-{6x^3y^2+8xy\over 3x^2y^2+4y}=-2x\nonumber \] не залежить від\(y\), тому теорема Template:index (a) застосовується з\(p(x)=-2x\). Так як\[\int p (x)\,dx=-\int 2x\,dx=-x^2,\nonumber \]\(\mu(x)=e^{-x^2}\) є інтегруючим фактором. Множення рівняння\ ref {eq:2.6.13} на\(\mu\) дає точне рівняння\[\label{eq:2.6.14} e^{-x^2}(2xy^3-2x^3y^3-4xy^2+2x)\,dx+ e^{-x^2}(3x^2y^2+4y)\,dy=0.\]
Щоб розв'язати це рівняння, ми повинні знайти\(F\) таку функцію, що\[\label{eq:2.6.15} F_x(x,y)=e^{-x^2}(2xy^3-2x^3y^3-4xy^2+2x)\] і\[\label{eq:2.6.16} F_y(x,y)=e^{-x^2}(3x^2y^2+4y).\] Інтеграція рівняння\ ref {eq:2.6.16} щодо\(y\) прибутковості\[\label{eq:2.6.17} F(x,y)=e^{-x^2}(x^2y^3+2y^2)+\psi(x).\] Диференціювання цього щодо\(x\) прибутковості\[F_x(x,y)=e^{-x^2}(2xy^3-2x^3y^3-4xy^2)+\psi'(x).\nonumber \] Порівняння цього з рівнянням\ ref {eq:2.6.15} показує, що \(\psi'(x)= 2xe^{-x^2}\); отже, ми можемо ввести\(\psi(x)=-e^{-x^2}\) Equation\ ref {eq:2.6.17} і зробити висновок, що\[e^{-x^2}\left(y^2(x^2y+2)-1\right)=c\nonumber \] це неявне рішення рівняння\ ref {eq:2.6.14}. Це також неявне рішення рівняння\ ref {eq:2.6.13}.
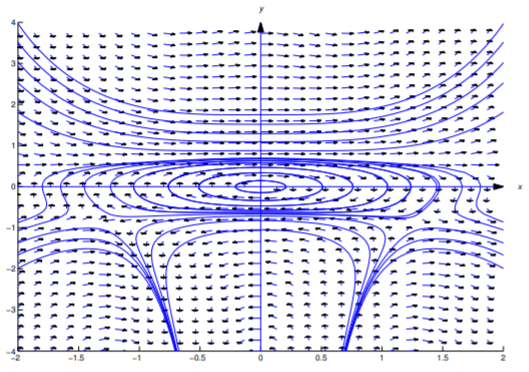
На малюнку Template:index показано поле напряму та деякі інтегральні криві для Рівняння\ ref {eq:2.6.13}
Знайдіть інтеграційний фактор для
\[\label{eq:2.6.30} 2xy^{3}dx+(3x^{2}y^{2}+x^{2}y^{3}+1)dy=0\]
і вирішити рівняння.
Рішення
У рівнянні\ ref {еква:2.6.30},
\[M=2xy^{3},\quad N=3x^{2}y^{2}+x^{2}y^{3}+1,\nonumber \]
і
\[M_{y}-N_{x}=6x^{2}-(6xy^{2}+2xy^{3})=-2xy^{3},\nonumber \]
так рівняння\ ref {eq:2.6.30} не є точним. Більш того,
\[\frac{M_y-N_x}{N}=-\frac{2xy^3}{3x^2y^2+x^2y^2+1}\nonumber \]
не є незалежним від\(y\), тому теорема 2.6.1 (а) не застосовується. Однак теорема 2.6.1 (b) дійсно застосовується, оскільки
\[\frac{N_x-M_y}{M}=\frac{2xy^3}{2xy^3}=1\nonumber \]
не є незалежним від\(x\), тому ми можемо взяти\(q(y)=1\). Так як
\[\int q(y)dy=\int dy=y,\nonumber \]
\(\mu (y)=e^{y}\)є інтеграційним фактором. Множення рівняння\ ref {eq:2.6.30} на\(\mu\) дає точне рівняння.
\[\label{eq:2.6.36} 2xy^{3}e^{y}dx+(3x^{2}y^{2}+x^{2}y^{3}+1)e^{y}dy=0.\]
Щоб вирішити це рівняння, ми повинні знайти\(F\) таку функцію, що
\[\label{eq:2.6.37} F_x (x,y)=2xy^{3}e^{y}\]
і
\[\label{eq:2.6.38} F_{y}(x,y)=(3x^{2}y^{2}+x^{2}y^{3}+1)e^{y}.\]
Інтеграція рівняння\ ref {eq:2.6.37} щодо\(x\) прибутковості
\[\label{eq:2.6.39} F (x,y)=x^{2} y^{3} e^{y} + \phi (y)\]
Диференціація цього щодо\(y\) врожайності
\[F_{y}= (3x^{2} y^{2} + x^{2} y^{3}) e^{y} + \phi ' (y)\nonumber \]
і порівняння цього з рівнянням\ ref {eq:2.6.38} показує, що φ 0 (y) = e y. Тому ми встановлюємо φ (y) = e y в Рівнянні\ ref {eq:2.6.39} і робимо висновок, що
\[(x^{2}y^{3}+1)e^{y}=c\nonumber \]
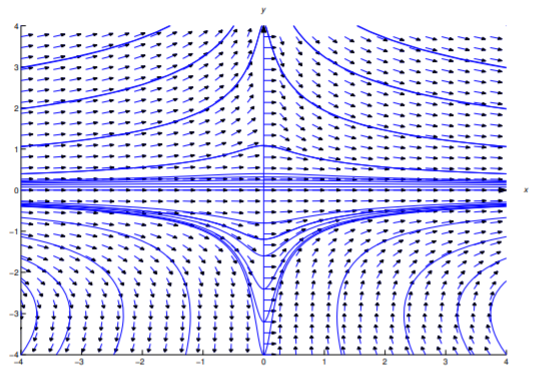
є неявним розв'язком\ ref {eq:2.6.36}. Це також неявне рішення\ ref {eq:2.6.30}. На малюнку Template:index показано поле напряму та деякі інтегральні криві для\ ref {eq:2.6.30}.
Теорема Template:index не застосовується в наступному прикладі, але більш загальний аргумент, який призвів до теореми Template:index, забезпечує інтеграційний коефіцієнт.
Знайдіть інтеграційний фактор для
\[\label{eq:2.6.42} (3xy+6y^{2})dx+(2x^{2} +9xy)dy=0\]
і вирішити рівняння.
Рішення
У рівнянні\ ref {еква:2.6.42}
\[M=3xy+6y^2, \quad N=2x^2+9xy,\nonumber \]
і
\[M_y -N_x =(3x+12y)-(4x+9y)=-x+3y.\nonumber \]
Тому
\[\frac{M_y - N_x}{M}=\frac{-x+3y}{3xy+6y^2}\quad\text{and}\quad\frac{N_x - M_y}{N}=\frac{x-3y}{2x^2 +9xy}\nonumber \]
тому теорема Template:index не застосовується. Слідуючи більш загальному аргументу, який призвів до теореми Template:index, ми шукаємо функції\(p = p(x)\) і\(q = q(y)\) такі, що
\[M_y - N_x = p(x)N-q(y)M;\nonumber \]
тобто,
\[-x+3y=p(x)(2x^2+9xy)-q(y)(3xy+6y^2).\nonumber \]
Оскільки ліва частина містить тільки перші терміни ступеня в\(x\) і\(y\), ми перепишемо це рівняння як
\[xp(x)(2x+9y)-yq(y)(3x+6y)=-x+3y.\nonumber \]
Це буде ідентичність, якщо
\[\label{eq:2.6.49} xp(x)=A\quad\text{and}yq(y)=B,\]
де\(A\) і\(B\) є константами такі, що
\[-x+3y=A(2x+9y)-B(3x+6y),\nonumber \]
або, рівнозначно,
\[-x+3y=(2A-3B)x+(9A-6B)y.\nonumber \]
Прирівнювання коефіцієнтів x і y з обох сторін показує, що останнє рівняння тримає для всіх,\((x, y)\) якщо
\[\begin{aligned} 2A-3B &=-1 \\ 9A-6B &=3 \end{aligned}\nonumber \]
який має розчин А = 1, В = 1. Тому рівняння\ ref {eq:2.6.49} означає, що
\[p(x)=\frac{1}{x}\quad\text{and}\quad q(y)=\frac{1}{y}.\nonumber \]
Так як
\[\int p(x)dx=\ln |x|\quad\text{and}\quad\int q(y)dy=\ln |y|,\nonumber \]
ми можемо дозволити\(P(x) = x\) і\(Q(y) = y\); отже,\(µ(x, y) = xy\) є інтеграційним фактором. Множення рівняння\ ref {eq:2.6.42} на\(µ\) дає точне рівняння
\[(3x^{2}y^{2}+6xy^{3})dx + (2x^{3}y+9x^{2}y^{2})dy=0.\nonumber \]
Ми залишаємо вам використовувати метод Розділу 2.5, щоб показати, що це рівняння має неявне рішення
\[\label{eq:2.6.55} x^{3}y^{2}+3x^{2}y^{3}=c.\]
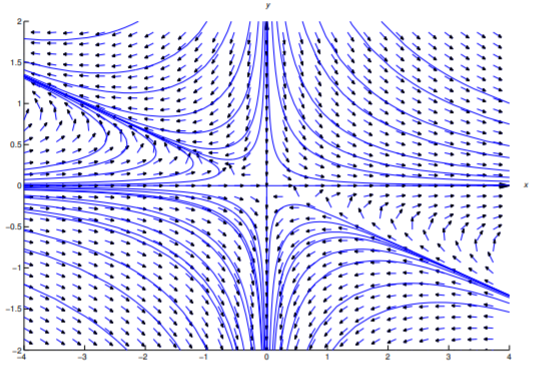
Це також неявне рішення рівняння\ ref {eq:2.6.42}. Оскільки x ≡ 0 і y ≡ 0 задовольняють рівняння\ ref {eq:2.6.55}, ви повинні перевірити, що x ≡ 0 і y ≡ 0 також є розв'язками рівняння\ ref {eq:2.6.42}. (Навіщо це перевіряти?) На малюнку Template:index показано поле напряму та інтегральні криві для Equation\ ref {eq:2.6.42}. Див. вправу 2.6.28 для загального обговорення рівнянь типу Рівняння\ ref {eq:2.6.42}.
Роздільне рівняння
\[\label{eq:2.6.56} -ydx+(x+x^{6})dy=0\]
може бути перетворений в точне рівняння
\[\label{eq:2.6.57} -\frac{dx}{x+x^{6}}+\frac{dy}{y}=0\]
шляхом множення на коефіцієнт інтеграції
\[\mu (x,y)=\frac{1}{y(x+x^{6})}.\nonumber \]
Однак для розв'язання Equation\ ref {eq:2.6.57} методом Розділу 2.5 нам доведеться оцінити неприємний інтеграл
\[\int\frac{dx}{x+x^{6}}.\nonumber \]
Натомість ми вирішуємо Equation\ ref {eq:2.6.56}\(y\) явним чином, знаходячи інтегруючий коефіцієнт форми\(µ(x, y) = x^{a}y^{b}\).
Рішення
У рівнянні\ ref {еква:2.6.56}
\[M=-y,\ N=x+x^6,\nonumber \]
і
\[M_y-N_x=-1-(1+6x^5)=-2-6x^5.\nonumber \]
Шукаємо функції\(p=p(x)\) і\(q=q(y)\) такі, що
\[M_y-N_x=p(x)N-q(y)M;\nonumber \]
тобто,
\[\label{eq:2.6.28} -2-6x^5=p(x)(x+x^6)+q(y)y.\]
У правій частині буде вказано термін\(-6x^5\) if\(p(x)=-6/x\). Тоді рівняння\ ref {eq:2.6.28} стає
\[-2-6x^5=-6-6x^5+q(y)y,\nonumber \]
так\(q(y)=4/y\). Так як
\[\int p(x)\,dx=-\int{6\over x}\,dx=-6\ln|x|=\ln{1\over x^6},\nonumber \]
і
\[\int q(y)\,dy=\int{4\over y}\,dy=4\ln |y|=\ln{y^4},\nonumber \]
ми можемо взяти\(P(x)=x^{-6}\) і\(Q(y)=y^4\), який дає інтеграційний фактор\(\mu(x,y)=x^{-6}y^4\). Множення рівняння\ ref {eq:2.6.56} на\(\mu\) дає точне рівняння
\[-{y^5\over x^6}\,dx+\left({y^4\over x^5}+y^4\right) \,dy=0.\nonumber \]
Ми залишаємо вам використовувати метод Розділу 2.5, щоб показати, що це рівняння має неявне рішення
\[\left({y\over x}\right)^5+y^5=k.\nonumber \]
Рішення для\(y\) врожайності
\[y=k^{1/5}x(1+x^5)^{-1/5},\nonumber \]
яку ми переписуємо як
\[y=cx(1+x^5)^{-1/5}\nonumber \]
перейменуванням довільної константи. Це також рішення рівняння\ ref {eq:2.6.56}.
На малюнку Template:index показано поле напряму та деякі інтегральні криві для Equation\ ref {eq:2.6.56}.