3.2: Роздільні рівняння
- Page ID
- 61278
Переглянути підручник на YouTube
Ода першого порядку відокремлюється, якщо її можна записати у формі, \[\label{eq:1}g(y)\frac{dy}{dx}=f(x),\quad y(x_0)=y_0,\]\(g(y)\)де функція\(f(x)\) не залежить від неї\(y\).\(x\) Інтеграція від\(x_0\) до\(x\) результатів\[\int_{x_0}^xg(y(x))y'(x)dx=\int_{x_0}^xf(x)dx.\nonumber\]
Інтеграл зліва може бути перетворений шляхом підстановки\(u = y(x),\: du = y'(x)dx\), і зміни нижньої і верхньої межі інтеграції на\(y(x_0) = y_0\) і\(y(x) = y\). Тому,\[\int_{y_0}^yg(u)du=\int_{x_0}^xf(x)dx,\nonumber\] і оскільки\(u\) є фіктивною змінною інтеграції, ми можемо написати це в еквівалентному вигляді \[\label{eq:2}\int_{y_0}^yg(y)dy=\int_{x_0}^xf(x)dx.\]
Простіша процедура, яка також дає,\(\eqref{eq:2}\) - це лікувати\(dy/dx\)\(\eqref{eq:1}\) як дріб. Множення\(\eqref{eq:1}\) на\(dx\) результати, в\[g(y)dy=f(x)dx,\nonumber\] якому є відокремлене рівняння з усіма залежними змінними на лівій стороні, а всі незалежні змінні з правого боку. Рівняння\(\eqref{eq:2}\) потім призводить безпосередньо після інтеграції.
Вирішити\(\frac{dy}{dx}+\frac{1}{2}y=\frac{3}{2}\), з\(y(0)=2\).
Рішення
Спочатку ми маніпулюємо диференціальним рівнянням до форми, \[\label{eq:3}\frac{dy}{dx}=\frac{1}{2}(3-y),\]а потім розглядаємо\(dy/dx\) так, ніби це дріб для розділення змінних:
\[\frac{dy}{3-y}=\frac{1}{2}dx.\nonumber\]
Ми інтегруємо праву сторону від початкової умови\(x = 0\) до\(x\) і ліву сторону від початкової умови\(y(0) = 2\) до\(y\). Відповідно, \[\label{eq:4}\int_2^y\frac{dy}{3-y}=\frac{1}{2}\int_0^xdx.\]
Інтеграли, які\(\eqref{eq:4}\) потрібно зробити. Зверніть увагу, що\(y(x) < 3\) для скінченного\(x\) або інтеграла з лівого боку розходиться. Тому\(3 − y > 0\) і інтеграція дає\[\begin{aligned} -\ln (3-y)]_2^y&=\frac{1}{2}x]_0^x, \\ \ln(3-y)&=-\frac{1}{2}x, \\ 3-y&=e^{-\frac{1}{2}x}, \\ y&=3-e^{-\frac{1}{2}x}.\end{aligned}\]
Оскільки це наше перше нетривіальне аналітичне рішення, розумно перевірити наш результат. Ми робимо це, диференціюючи наше рішення:
\[\begin{aligned}\frac{dy}{dx}&=\frac{1}{2}e^{-\frac{1}{2}x} \\ &=\frac{1}{2}(3-y);\end{aligned}\]і перевірка початкових умов,\(y(0) = 3 − e^0 = 2\). Тому наше рішення задовольняє як вихідну оду, так і початкову умову.
Вирішити\(\frac{dy}{dx}+\frac{1}{2}y=\frac{3}{2},\) с\(y(0)=4\).
Рішення
Це ідентичне диференціальне рівняння, як і раніше, але з різними початковими умовами. Ми перейдемо безпосередньо до кроку інтеграції:
\[\int_4^y\frac{dy}{3-y}=\frac{1}{2}\int_0^xdx.\nonumber\]
Тепер\(y(x) > 3\), так що\(y − 3 > 0\) і інтеграція дає\[\begin{aligned}-\ln (y-3)]_4^y&=\frac{1}{2}x]_0^x, \\ \ln(y-3)&=-\frac{1}{2}x, \\ y-3&=e^{-\frac{1}{2}x}, \\ y&=3+e^{-\frac{1}{2}x}.\end{aligned}\]
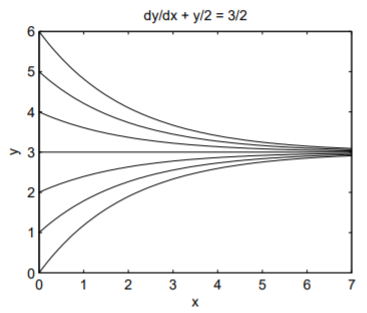
Криві розв'язку для діапазону початкових умов представлені на рис. \(\PageIndex{1}\). Всі розв'язки мають горизонтальну асимптоту\(y = 3\) при якій\(dy/dx = 0\). Для\(y(0) = y_0\), загальне рішення може бути показано\(y(x) = 3 + (y_0 − 3) \text{exp}(−x/2)\).
Вирішити\(\frac{dy}{dx}=\frac{2\cos 2x}{3+2y}\), з\(y(0)=-1\).
- Для яких\(x>0\) значень рішення існує?
- Для чого значення\(x>0\)\(y(x)\) максимальне?
Рішення
Зверніть увагу, що похідна\(y\) розходиться коли\(y = −3/2\), і що це може спричинити деякі проблеми з рішенням.
Вирішуємо оду, відокремлюючи змінні та інтегруючи з початкових умов:
\[\begin{aligned} (3+2y)dy&=2\cos 2xdx \\ \int_{-1}^y(3+2y)dy&=2\int_0^x\cos 2xdx \\ 3y+y^2]_{-1}^y&=\sin 2x]_0^x \\ y^2+3y+2-\sin 2x&=0 \\ y_{\pm} &=\frac{1}{2}[-3\pm\sqrt{1+4\sin 2x}].\end{aligned}\]
Розв'язування квадратного рівняння для\(y\) ввів помилковий розв'язок, який не задовольняє початковим умовам. Ми тестуємо:
\[y_{\pm}(0)=\frac{1}{2}[-3\pm 1]=\left\{\begin{array}{c}-1; \\ -2.\end{array}\right.\nonumber\]
Тільки\(+\) корінь задовольняє початковій умові, так що унікальним рішенням оди і початкової умови є \[\label{eq:5} y=\frac{1}{2}[-3+\sqrt{1+4\sin 2x}].\]
Щоб визначити (i) значення,\(x > 0\) для яких існує рішення, ми вимагаємо\[1+4\sin 2x\geq 0,\nonumber\] або \[\label{eq:6}\sin 2x\geq -\frac{1}{4}.\]
Зверніть увагу, що в\(x = 0\), у нас є\(\sin 2x = 0\); в\(x = π/4\),\(\sin 2x = 1;\) у нас є\(x = π/2\), ми маємо\(\sin 2x = 0\); і в\(x = 3π/4\), у нас є\(\sin 2x = −1\). Тому нам потрібно визначити значення\(x\) такого\(\sin 2x = −1/4\), що, з\(x\) в діапазоні\(π/2 < x < 3π/4\). Розв'язок оди буде існувати для всіх\(x\) між нулем і цим значенням.
Щоб вирішити\(\sin 2x = −1/4\) для\(x\) в інтервалі\(π/2 < x < 3π/4\), потрібно згадати визначення\(\text{arcsin}\), або\(\sin^{−1}\), як це знайдено на типовому науковому калькуляторі. Зворотна функція\[f(x)=\sin x,\quad -\pi /2\leq x\leq \pi /2\nonumber\] позначається символом\(\text{arcsin}\). Перше рішення з\(x > 0\) рівняння\(\sin 2x = −1/4\) розміщує\(2x\) в інтервалі\((π, 3π/2)\), тому, щоб інвертувати це рівняння, використовуючи те, що\(\text{arcsine}\) нам потрібно застосувати ідентичність\(\sin (π − x) = \sin x\), і переписати\(\sin 2x = −1/4\) як\(\sin (π − 2x) = −1/4\). Розв'язок цього рівняння можна потім знайти, взявши\(\text{arcsine}\), і є\[\pi -2x=\text{arcsin}(-1/4),\nonumber\] або\[x=\frac{1}{2}\left(\pi +\text{arcsin}\frac{1}{4}\right).\nonumber\]
Тому рішення існує для того\(0 ≤ x ≤ (π + \text{arcsin} (1/4)) /2 = 1.6971\ldots\), де ми використовували калькулятор значення (обчислення в радіанах), щоб знайти\(\text{arcsin}(0.25) = 0.2527\ldots\). На\((x, y) = (1.6971\ldots , −3/2)\) значенні крива рішення закінчується і\(dy/dx\) стає нескінченною.
Щоб визначити (ii) значення\(x\) при якому\(y = y(x)\) максимальне, досліджуємо\(\eqref{eq:5}\) безпосередньо. Значення\(y\) буде максимальним, коли\(\sin 2x\) прийме його максимальне значення за інтервал, де існує рішення. Це буде коли\(2x = π/2\), або\(x = π/4 = 0.7854\ldots\).
Графік роботи\(y=y(x)\) наведено на рис.3.3.1.
