3.1: Метод Ейлера

Last updated
Save as PDF

Page ID: 61284

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Переглянути підручник на YouTube

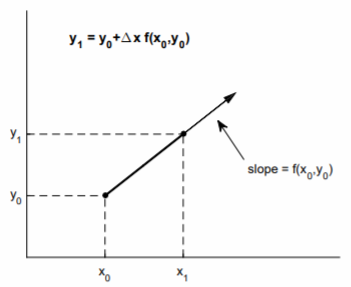
Хоча не завжди вдається знайти аналітичне рішення (3.1) для\(y = y(x)\), завжди можна визначити унікальне числове рішення, задане початкове значення\(y(x_0) = y_0\), і за умови\(f(x, y)\) є добре поведеною функцією. Диференціальне рівняння (3.1) дає нам нахил\(f(x_0, y_0)\) дотичної лінії до кривої розв'язку\(y = y(x)\) в точці\((x_0, y_0)\). При невеликому розмірі\(∆x = x_1 − x_0\) кроку початкова умова\((x_0, y_0)\) може бути маршована вперед\((x_1, y_1)\) по дотичній лінії методом Ейлера (див. Рис. \(\PageIndex{1}\))\[y_1=y_0+\Delta xf(x_0, y_0).\nonumber\]

\((x_1, y_1)\)Потім це рішення стає новою початковою умовою і марширується вперед\((x_2, y_2)\) вздовж щойно визначеної дотичної лінії з нахилом, заданим\(f(x_1, y_1)\). Для досить\(∆x\) малих числове рішення сходиться до точного рішення.

Малюнок\(\PageIndex{1}\):\(dy/dx = f(x, y),\)\(y(x_0) = y_0,\) Диференціальне рівняння інтегровано з\(x = x_1\) використанням методу Ейлера\(y_1 = y_0 + ∆x f(x_0, y_0)\), с\(∆x = x_1 − x_0\).