2.1: Заява про конгруентність
- Page ID
- 58822
Кажуть, що два трикутники є конгруентними, якщо один можна розмістити над іншим так, щоб вони збігалися (поєднувалися). Це означає, що конгруентні трикутники є точними копіями один одного, і коли вони розташовані разом, сторони і кути, які збігаються, називаються відповідними сторонами і кутами, рівні.
На малюнку\(\PageIndex{1}\),\(\triangle ABC\) це конгруентно\(\triangle DEF\). Символ конгруентності є\(\cong\) і пишемо\(\triangle ABC \cong \triangle DEF\). \(\angle A\)відповідає\(\angle D\)\(\angle E\),\(\angle B\) відповідає і\(\angle C\) відповідає\(\angle F\). Сторона\(AB\)\(DE, BC\) відповідає відповідає\(EF\), і\(AC\) відповідає\(DF\).
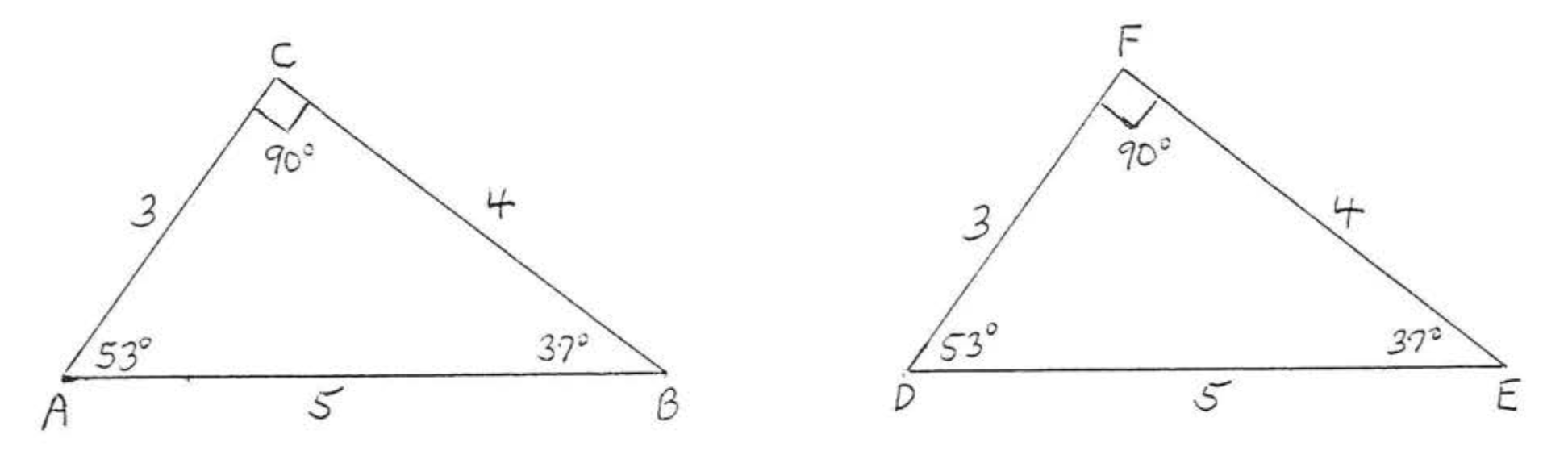
У цій книзі конгруентність заяву завжди\(\triangle ABC \cong \triangle DEF\) буде написано так, що відповідні вершини з'являються в тому ж порядку, Для трикутників на малюнку\(\PageIndex{1}\), ми також могли б написати\(\triangle BAC \cong \triangle EDF\) або,\(\triangle ACB \cong \triangle DFE\) але ніколи, наприклад,\(\triangle ABC \cong \triangle EDF\) ні\(\triangle ACB \cong \triangle DEF\). (Будьте обережні, що не всі підручники дотримуються цієї практики, Багато авторів будуть писати листи без урахування наказу. Якщо це так, то ми не можемо сказати, які частини відповідають із заяви про конгруентність).
Тому ми завжди можемо сказати, які частини відповідають саме з конгруентності. Наприклад, враховуючи це\(\triangle ABC \cong \triangle DEF\), сторона\(AB\) відповідає стороні,\(DE\) оскільки кожна складається з перших двох літер,\(AC\) відповідає DF, оскільки кожна складається з першої та останньої літер,\(BC\) відповідає\(EF\) тому, що кожна складається з останніх двох літер.
Якщо\(\triangle PQR \cong \triangle STR\)
- перерахуйте відповідні кути і сторони;
- знайти\(x\) і\(y\).

Рішення
(1)
\(\begin{array} {rcll} {\underline{\triangle PQR}} & \ & {\underline{\triangle STR}} & {} \\ {\angle P} & = & {\angle S} & {\text{(first letter of each triangle in congruence statement)}} \\ {\angle Q} & = & {\angle T} & {\text{(second letter)}} \\ {\angle PRQ} & = & {\angle SRT} & {\text{(third letter. We don't write "}\angle R = \angle R \text{" since}} \\ {} & & {} & {\text{each }\angle R \text{ is different)}} \\ {PQ} & = & {ST} & {\text{(first two letters)}} \\ {PR} & = & {SR} & {\text{(firsst and last letters)}} \\ {QR} & = & {TR} & {\text{(last two letters)}} \end{array}\)
(2)
\(x = PQ = ST = 6\).
\(y = PR = SR = 8\).
Відповідь (2):\(x = 6, y = 8\).
Припускаючи\(\triangle I \cong \triangle II\), напишіть заяву про конгруентність для\(\triangle I\) і\(\triangle II\):
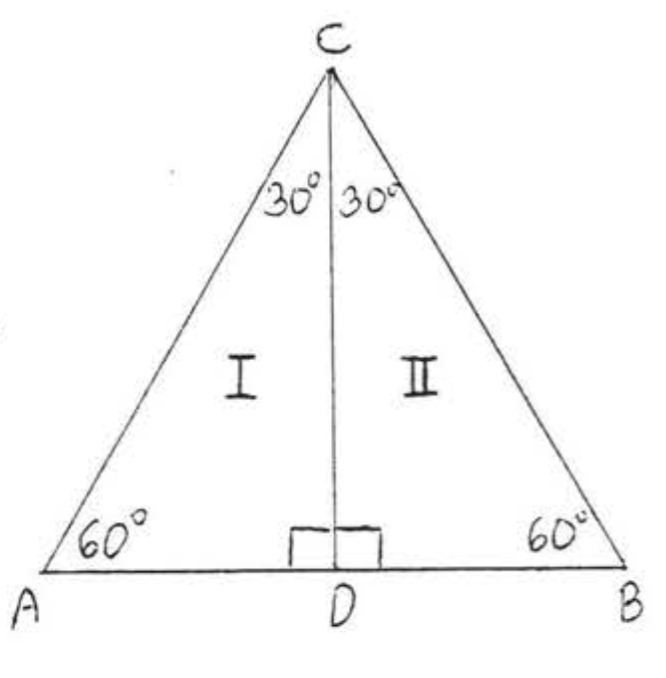
Рішення
\(\begin{array} {rcll} {\triangle I} & \ & {\triangle II} & {} \\ {\angle A} & = & {\angle B} & {(\text{both = } 60^{\circ})} \\ {\angle ACD} & = & {\angle BCD} & {(\text{both = } 30^{\circ})} \\ {\angle ADC} & = & {\angle BDC} & {(\text{both = } 90^{\circ})} \end{array}\)
Тому
Відповідь:\(\triangle ACD \cong \triangle BCD\).
Припускаючи\(\triangle I \cong \triangle II\), напишіть заяву про конгруентність для\(\triangle I\) і\(\triangle II\):

Рішення
Кути, які позначені таким же чином, приймаються рівними.
\(\begin{array} {rcll} {\underline{\triangle I}} & \ & {\underline{\triangle II}} & {} \\ {\angle A} & = & {\angle B} & {(\text{both marked with one stroke})} \\ {\angle ACD} & = & {\angle BCD} & {(\text{both marked with two strokes})} \\ {\angle ADC} & = & {\angle BDC} & {(\text{both marked with three strokes})} \end{array}\)
Відносини такі ж, як у прикладі\(\PageIndex{2}\).
Відповідь:\(\triangle ACD \cong \triangle BCD\).
Проблеми
1 - 4. Для кожної пари конгруентних трикутників
(1) перерахуйте відповідні сторони та кути;
(2) знайти\(x\) і\(y\).
1. \(\triangle ABC \cong \triangle DEF\).

2. \(\triangle PQR \cong \triangle STU\).

3. \(\triangle ABC \cong \triangle CDA\).

4. \(\triangle ABC \cong \triangle EDC\).

5 - 10. Напишіть заяву про конгруентність для кожного з наступних. Припустимо, що трикутники є конгруентними і що кути або сторони, позначені таким же чином, рівні.
5.  6.
6. 
7.  8.
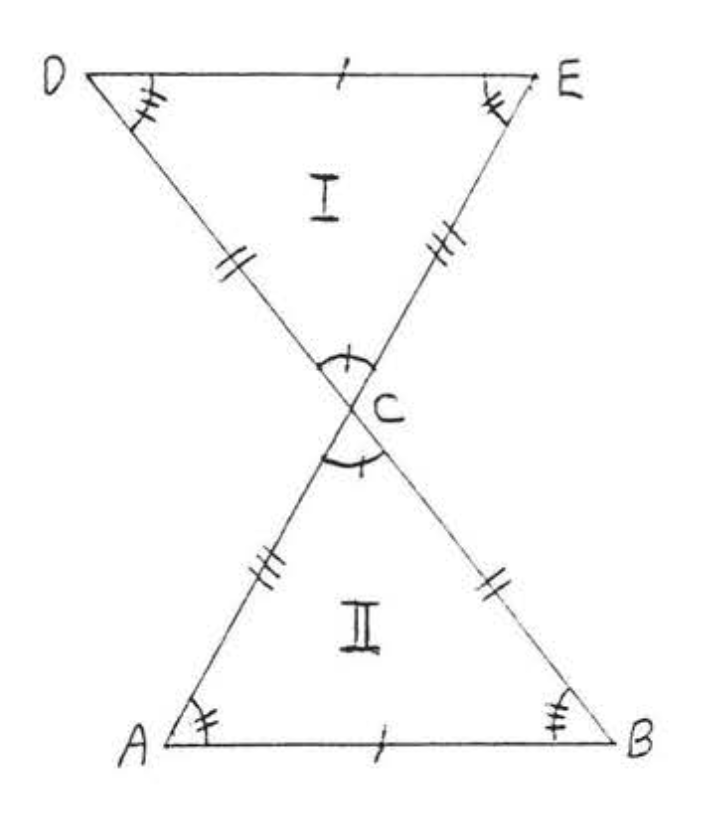
8. 
9. 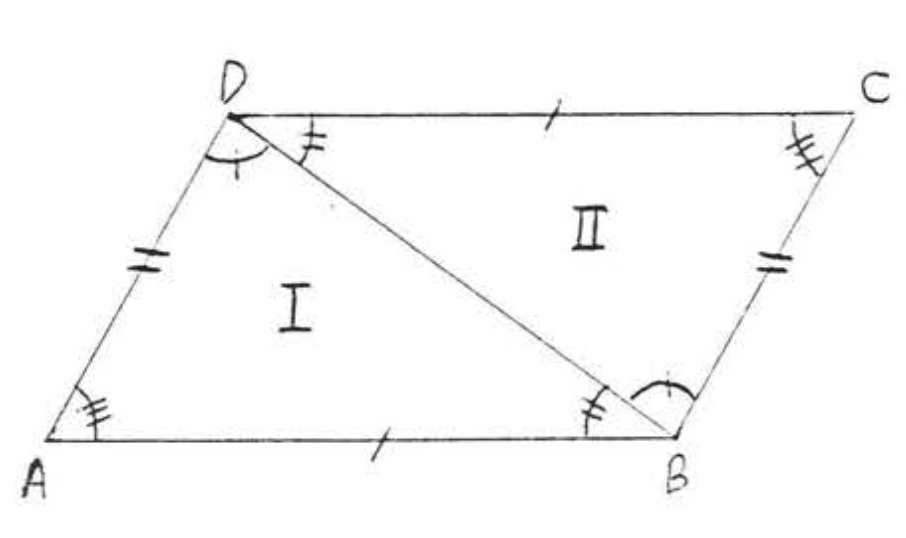 10.
10. 
