2.6: Теорема ССС
- Page ID
- 58835
Розглянемо тепер випадок, коли сторона двох трикутників, як відомо, має однакову довжину.
Два трикутника є конгруентними, якщо три сторони одного дорівнюють відповідно трьом сторонам іншого (\(SSS = SSS\)).
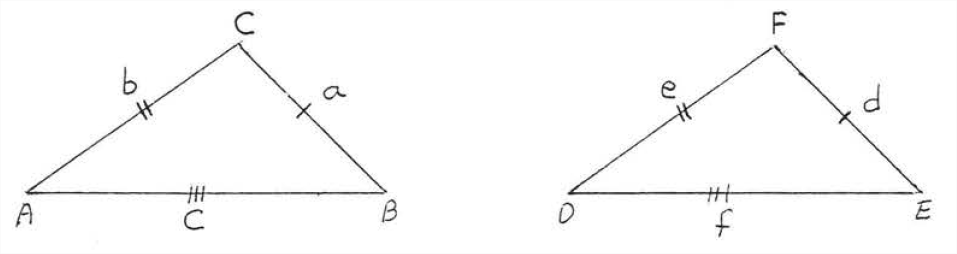
Теорема\(\PageIndex{1}\) продемонстрована на малюнку\(\PageIndex{1}\): якщо\(a=d, b=e,\) і\(c=f\) тоді\(\triangle ABC \cong \triangle DEF\)
Знайти\(x, y, z:\)
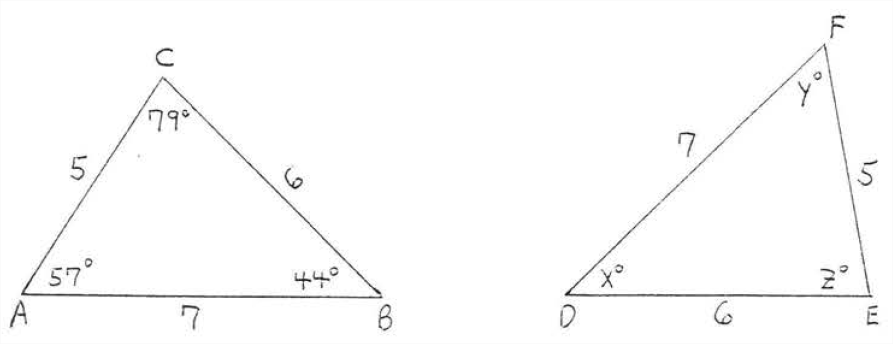
Рішення
\(AB = 7 = DF\). Тому кут\(\angle C,\), протилежний АВ, повинен відповідати тому\(\angle E\), що кут протилежний\(DF\). Таким же чином\(\angle A\) відповідає\(\angle F\) і\(\angle B\) відповідає\(\angle D\). У нас\(\triangle ABC \cong \triangle FDE\) за допомогою\(SSS = SSS\), так
\(x^{\circ}=\angle D=\angle B=44^{\circ}\)
\(y^{\circ}=\angle F=\angle A=57^{\circ}\)
\(z^{\circ}=\angle E=\angle C=79^{\circ}\)
Відповідь:\(x = 44, y=57, z=79\)
На малюнку\(\PageIndex{1}\) розташуйте\(\triangle ABC\) і\(\triangle DEF\) так, щоб їх найдовші сторони збігалися, в даному випадку\(AB\) і\(DE\). Це можна зробити тому, що\(AB = c= r = DE.\) тепер малюємо\(CF\), формуючи кути\(1,2,3,\) і 4 (рис.\(\PageIndex{2}\)). Решта доказів буде представлена у вигляді подвійних стовпців:
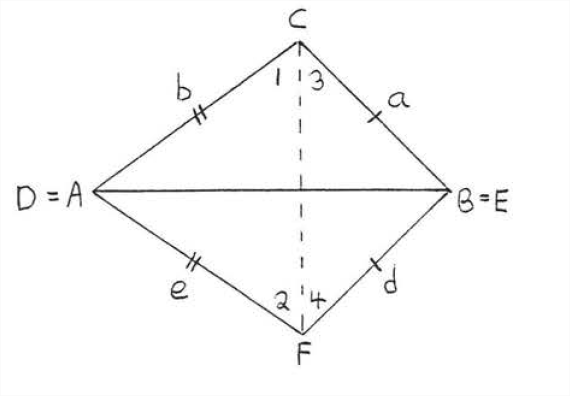
| Заява | причини |
| 1. \(\angle 1 = \angle 2\). | 1. \(CAF\)Базові кути рівнобедреного трикутника рівні (Теорема\(\PageIndex{1}\), section 2.5). |
| 2. \(\angle 3 = \angle 4\). | 2. \(CBF\)Базові кути рівнобедреного трикутника рівні. |
| 3. \(\angle C = \angle F\). | 3. \(\angle C = \angle 1 + \angle 3 = \angle 2 + \angle 4 = \angle F\). |
| 4. \(AC = DF\). | 4. З огляду на,\(AC = b = e = DF\). |
| 5. \(BC = EF\). | 5. З огляду на,\(BC = a = d = EF\). |
| 6. \(\triangle ABC \cong \triangle DEF\). | 6. \(SAS = SAS\):\(AC, \angle C, BC\)\(\triangle ABC = DF\) оф\(\angle F\),\(EF\) оф\(\triangle DEF\). |
Дано\(AB = DE, BC = EF,\) і\(AC = DF\). Довести\(\angle C = \angle F\)
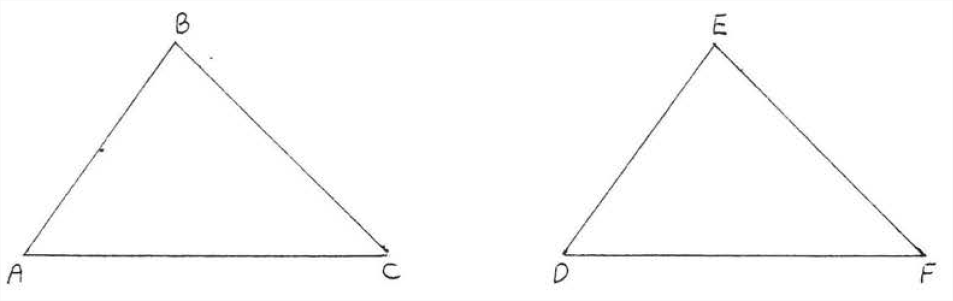
Рішення
| Заяви | причини |
| 1. \(AB = DE\). | 1. Дано. |
| 2. \(BC = EF\). | 2. Дано. |
| 3. \(AC = DF\). | 3. Дано. |
| 4. \(\triangle ABC \cong \triangle DEF\). | 4. \(SSS = SSS\):\(AB, BC, AC\) з\(\triangle ABC = DE\),\(EF, DF\) з\(\triangle DEF\). |
| 5. \(\angle C = \angle F\). | 5. Відповідні кути конгруентних трикутників рівні. |
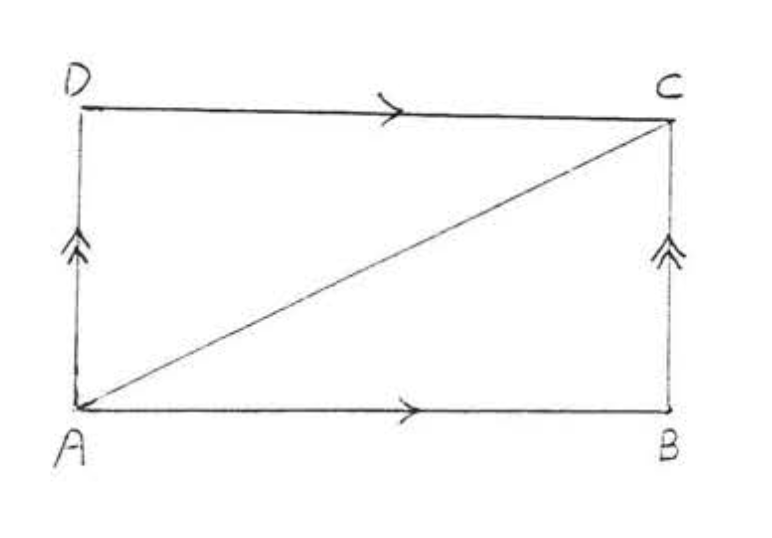
Теорема ССС є основою важливого принципу будівельної техніки, який називається трикутним кріпленням. Уявіть собі відрізки лінії\(\PageIndex{3}\) на малюнку, щоб бути боби з дерева або сталі, з'єднані в кінцевих точках цвяхами або гвинтами. Якщо натиснути на одну зі сторін,\(ABCD\) буде руйнуватися і виглядати\(A'B'C'D'\).
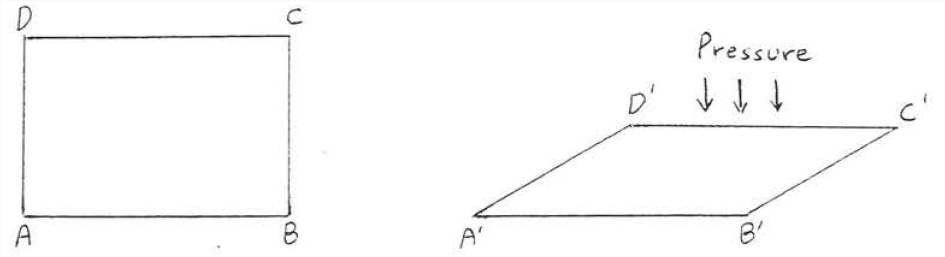
Тепер припустимо точки\(A\) і\(C\) з'єднуються новою балкою, званої дужкою (рис.\(\PageIndex{4}\)). Структура не зруйнується до тих пір, поки боби залишаться цілими і з'єднаними між собою. Неможливо деформуватися\(ABCD\) в будь-яку іншу форму,\(A'B'C'D'\) тому що якщо\(AB = A'B'\)\(BC = B'C'\), і\(AC = A'C'\) тоді\(\triangle ABC\) буде конгруентно до\(\triangle A'B'C'\) мимо\(SSS = SSS\).
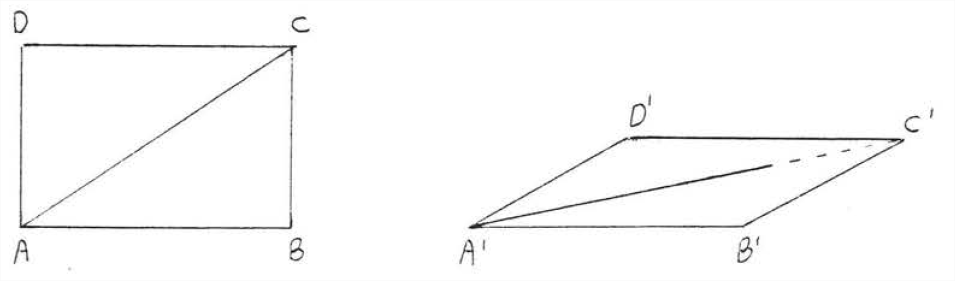
Іноді ми говоримо, що трикутник - це жорстка фігура; як тільки сторони трикутника зафіксовані, кути не можуть бути змінені. Таким чином\(\PageIndex{4}\), на малюнку, форма\(\triangle ABC\) не може бути змінена до тих пір, поки довжини його сторін залишаються однаковими.
Проблеми
1 - 8. Для кожного з наступних (1) напишіть заяву про конгруентність,
(2) з огляду на причину (1) (\(SAS\),,\(ASA\)\(AAS\), або\(SSS\) теорема), і
(3) знайти\(x\), або\(x\) і\(y\), або\(x, y\), і\(z\).
1.
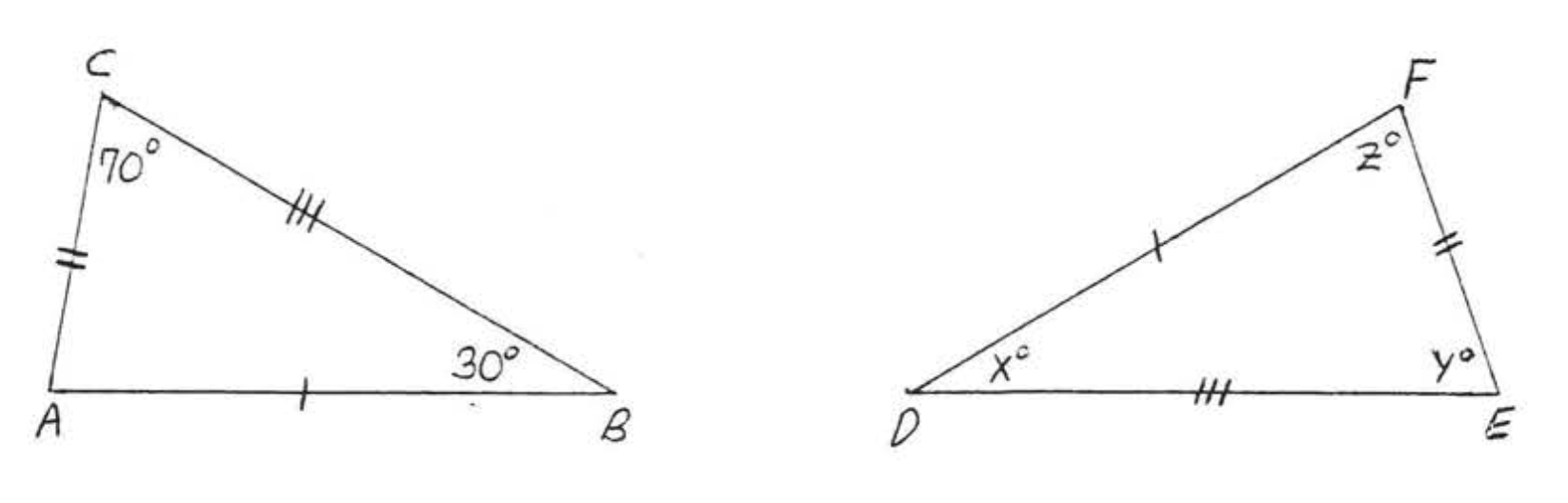
2.
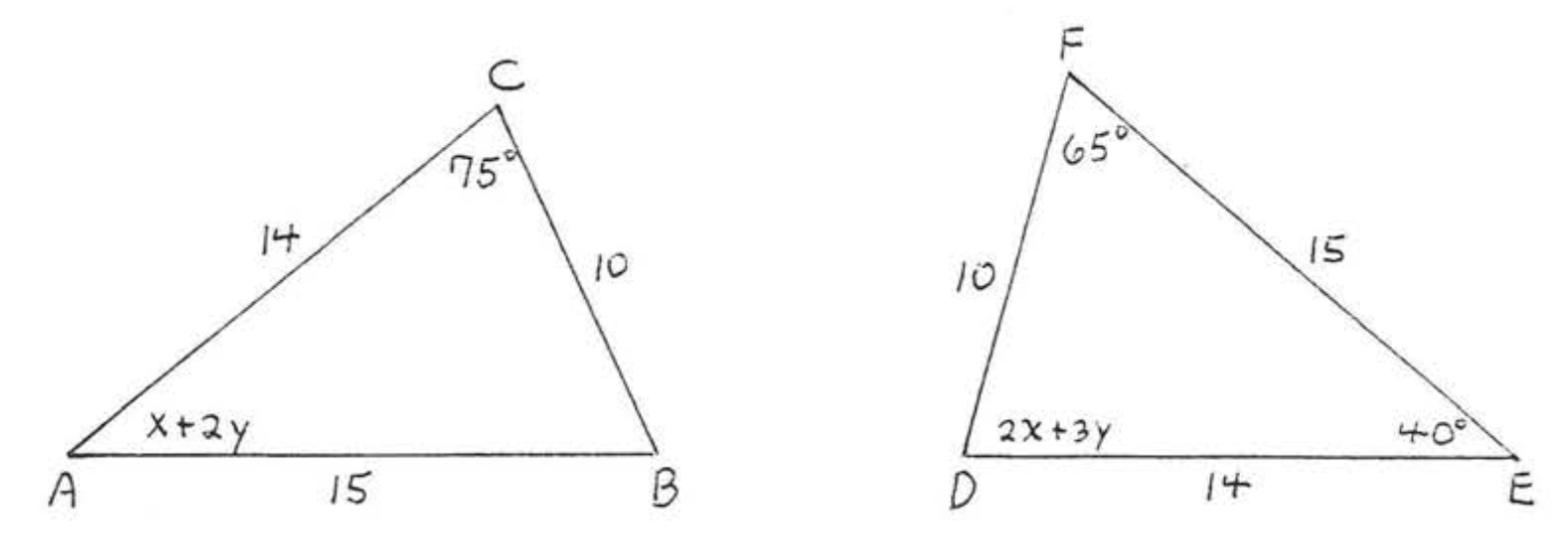
3.
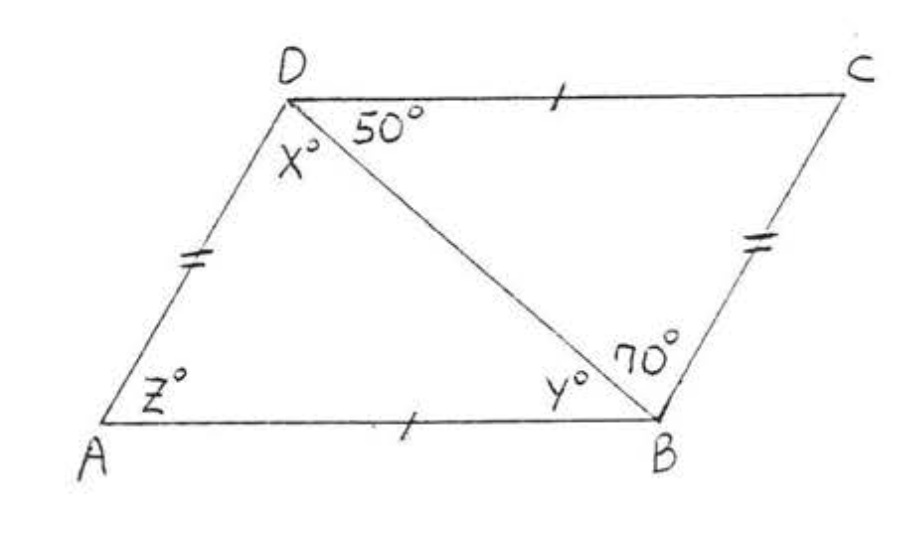
4.
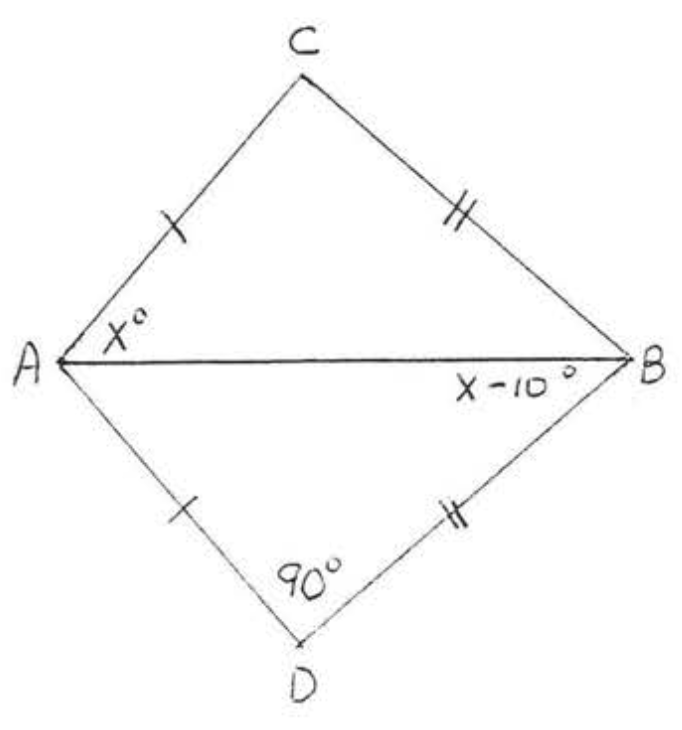
5.
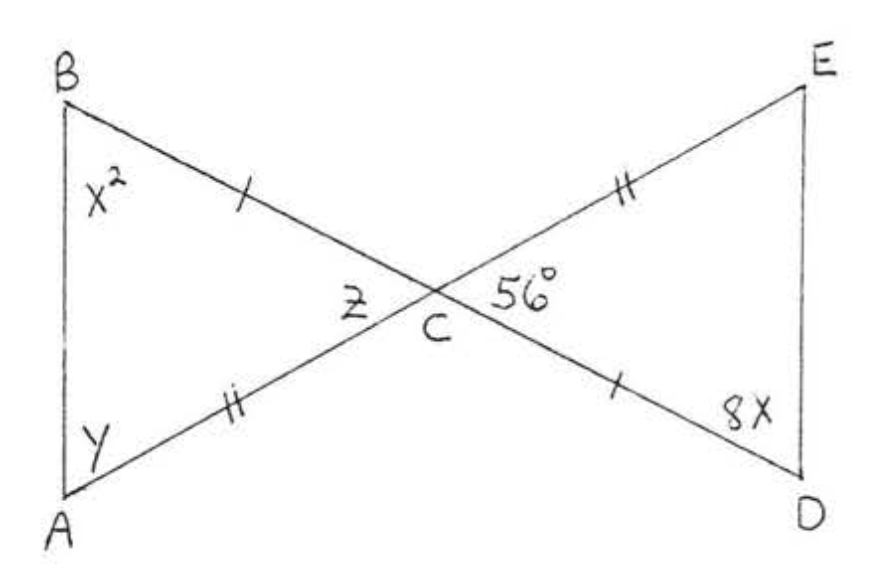
6.
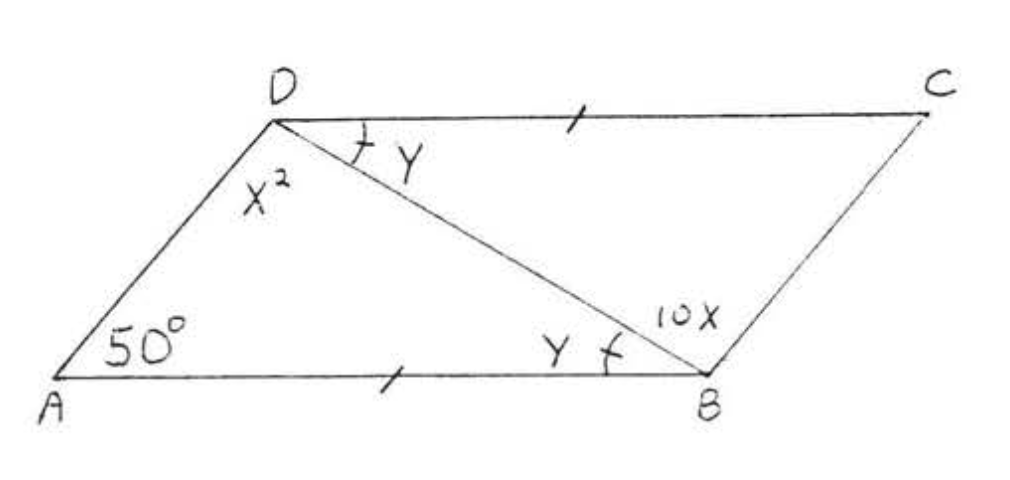
7.
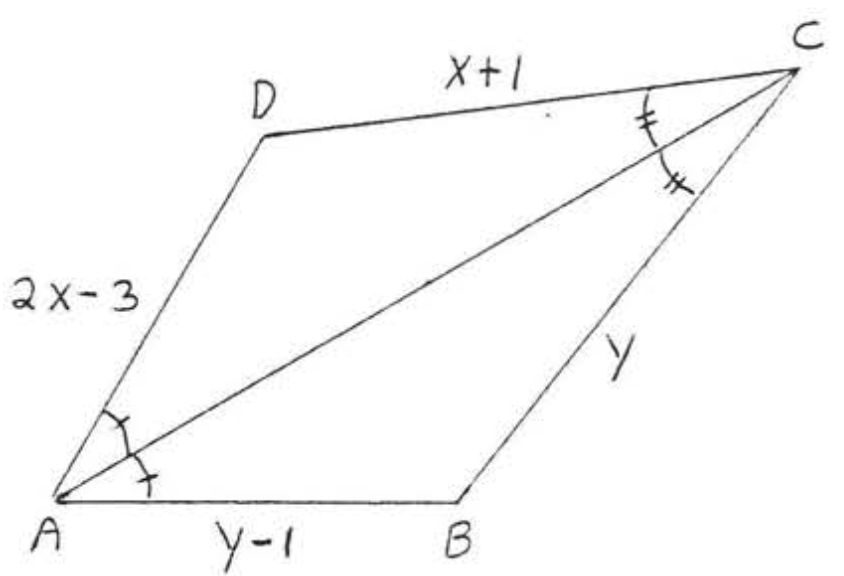
8.
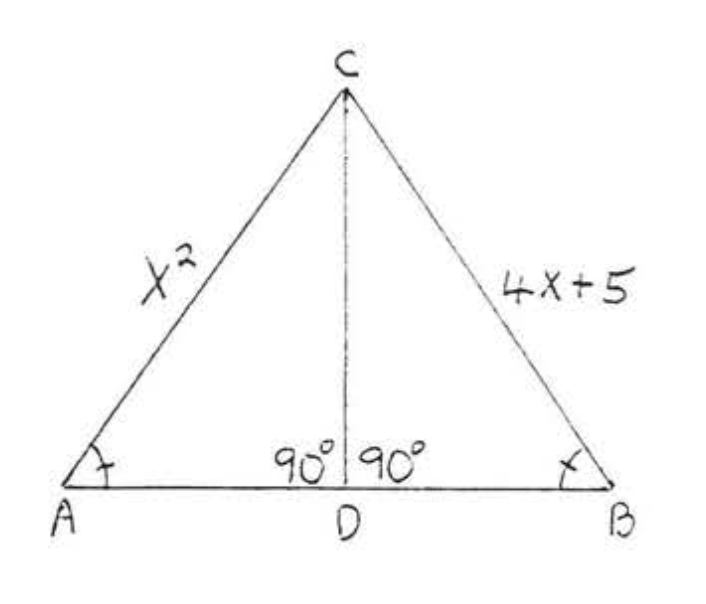
9. З огляду на\(AB = DE\)\(BC = EF\),, і\(AC = DF\). Доведіть\(\angle A = \angle D\).
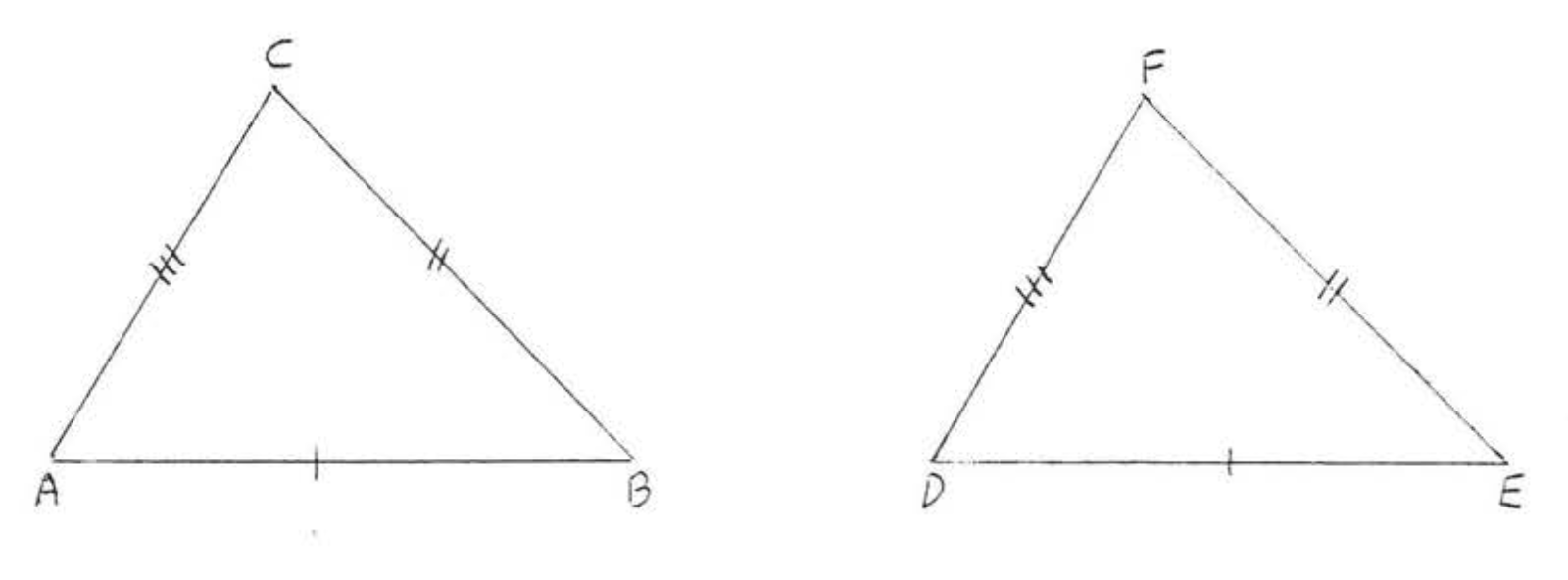
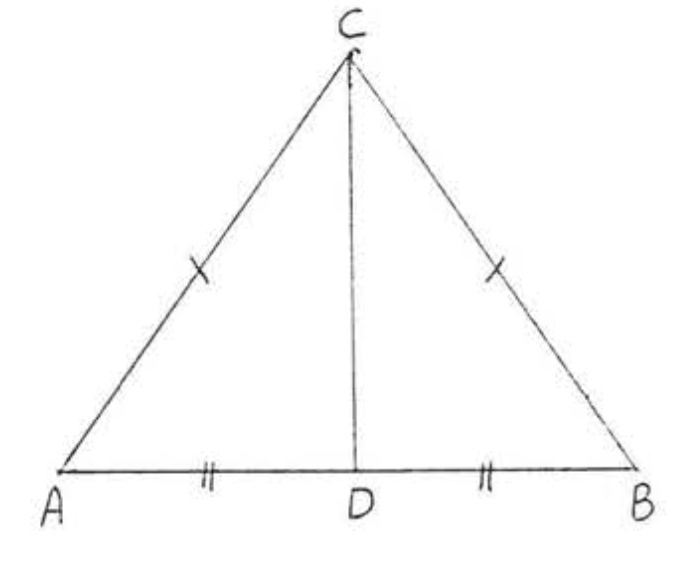
10. Дано\(AC = BC\). \(AD = BD\). Доведіть\(\angle ADC = \angle BDC\).
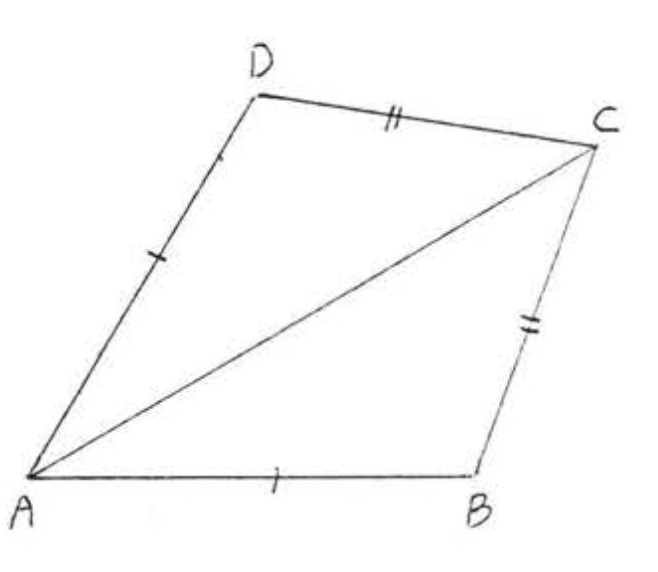
11. З огляду\(AB = AD\) на,\(BC = DC\). Доведіть\(\angle BAC = \angle CAD\).
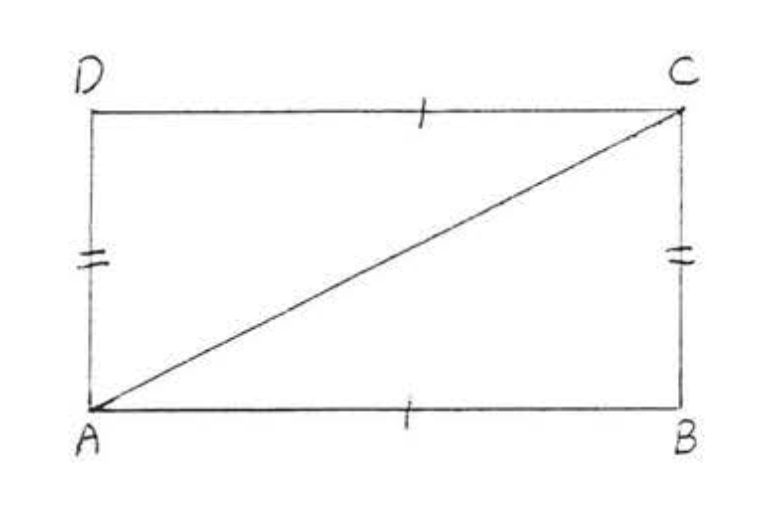
12. З огляду\(AB = CD\) на,\(BC = DA\). Доведіть\(\angle BAC = \angle DCA\).
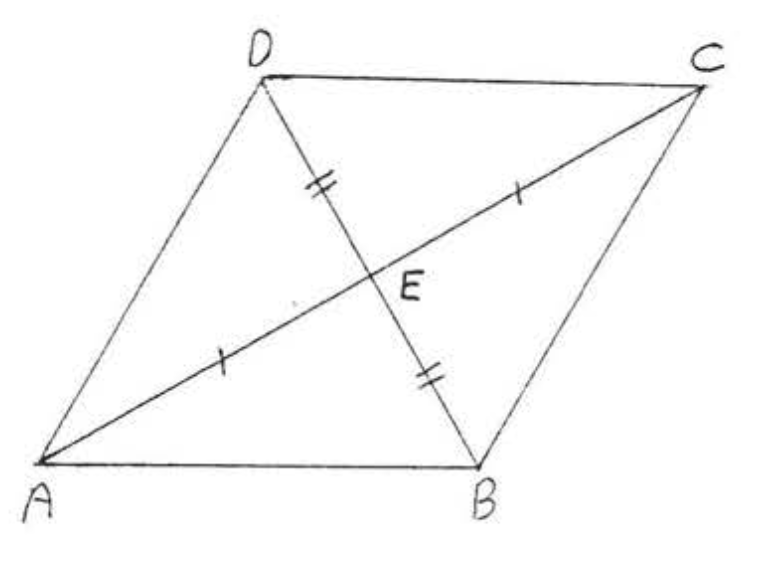
13. З огляду\(AE = CE\) на,\(BE = ED\). Доведіть\(AB = CD\).
14. З огляду\(AB||CD\) на,\(AD||BC\). Доведіть\(AB = CD\).