1.2: Кути
- Page ID
- 58791
Кут - це фігура, утворена двома променями із загальною кінцевою точкою, Два промені називаються сторонами кута, а загальна кінцева точка називається вершиною кута, Символ кута є\(\angle\)

Кут на малюнку\(\PageIndex{1}\) має вершину\(A\)\(AB\) і сторони і\(AC\), позначається\(\angle BAC\) або\(\angle CAB\) або просто\(\angle A\). Коли три літери використовуються, середня літера завжди вершина, На малюнку\(\PageIndex{2}\) ми не будемо використовувати позначення\(\angle A\) як абревіатуру для\(\angle BAC\) тому що це також може означати\(\angle CAD\) або\(\angle BAD\), Однак ми могли б використовувати більш просте ім'я\(\angle x\) для\(\angle BAC\) якщо "\(x\)" є позначені, як показано,
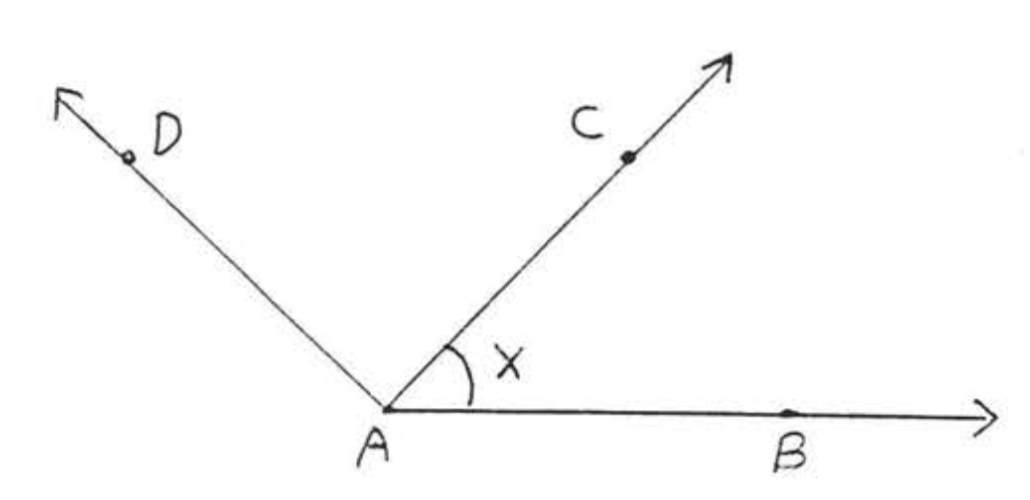
Кути можна виміряти за допомогою приладу, званого транспортиром. Одиниця виміру називається градусом, а символом ступеня є\(^{\circ}\).
Щоб виміряти кут, помістіть центр транспортира (часто позначеного хрестом або маленьким колом) на вершині кута, розташуйте транспортир так, щоб одна сторона кута прорізалася поперек 0, на початку шкали, і так, щоб інша сторона прорізала точку далі вгору по шкалі, використовуємо або верхня шкала, або нижня шкала, залежно від того, що зручніше, Наприклад, на малюнку одна сторона\(\angle BAC\) хрестиків 0 на нижній шкалі\(\PageIndex{3}\), а інша сторона перетинає 50 на нижній шкалі. Тому міра\(\angle BAC\) є,\(50^{\circ}\) і ми пишемо\(\angle BAC\) =\(50^{\circ}\).

На\(\PageIndex{4}\) малюнку сторона\(\overrightarrow AD\)\(\angle DAC\) хрестиків 0 на верхній шкалі. Тому дивимося на верхній шкалі точку, в якій\(\overrightarrow{AC}\) перетинаються і робимо висновок, що\(\angle DAC = 130^{\circ}\).

Намалюйте кут\(40^{\circ}\) і позначте його\(\angle BAC\).
Рішення
Намалюйте промінь,\(\overrightarrow{AB}\) використовуючи прямий край:

Розмістіть транспортир так, щоб його центр збігався з\(A\) і\(\overrightarrow{AB}\) перетинав шкалу в 0:

Відзначте місце на транспортирі відповідне\(40^{\circ}\). Позначте цей пункт\(C\):

З'єднатися\(A\) з\(C\):

Два кути, як кажуть, рівні, якщо вони мають однакову міру в градусах. Ми часто вказуємо два кути рівні, розмічаючи їх однаково. На малюнку\(\PageIndex{5}\),\(\angle A = \angle B\).

Бісектриса кута - це промінь, який ділить кут на два рівні кути. На малюнку\(\PageIndex{6}\),\(\overrightarrow{AC}\) це кут бісектриси\(\angle BAD\). Ми також говоримо\(\overrightarrow{AC}\) бісекти\(\angle BAD\).

Знайти,\(x\) якщо\(\overrightarrow{AC}\) бісекти\(\angle BAD\) і\(\angle BAD = 80^{\circ}\):

Рішення
\(x^{\circ} = \dfrac{1}{2} \angle BAD = \dfrac{1}{2} (80^{\circ}) = 40^{\circ}\)
Відповідь:\(x = 40\).
Знайти,\(x\) якщо\(\overrightarrow{AC}\) бісекти\(\angle BAD\):

Рішення
\[\begin{array} {rcl} {\angle BAC} & = & {\angle CAD} \\ {\dfrac{7}{2} x} & = & {3x + 5} \\ {(2) \dfrac{7}{2} x} & = & {(2) (3x + 5)} \\ {7x} & = & {6x + 10} \\ {7x - 6x} & = & {10} \\ {x } & = & {10} \end{array}\]
Перевірка:

Відповідь:\(x = 10\).
Проблеми
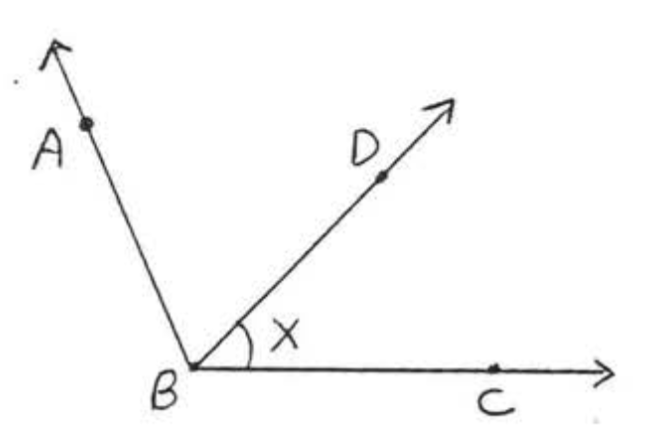
1 - 6. Для кожної фігури дайте іншу назву для\(\angle x\):
1. 
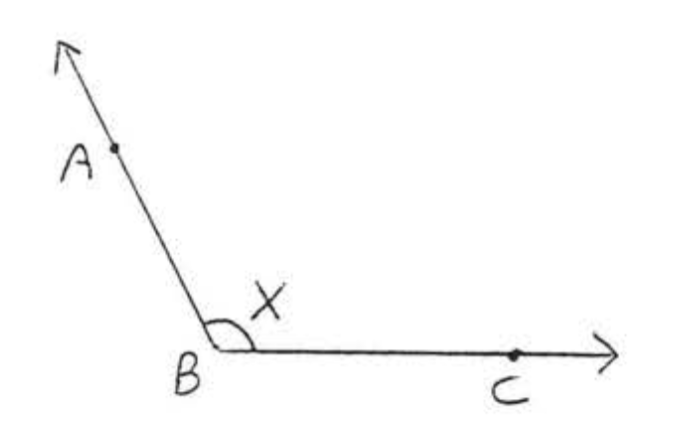
2. 
3. 
4. 
5. 
6. 
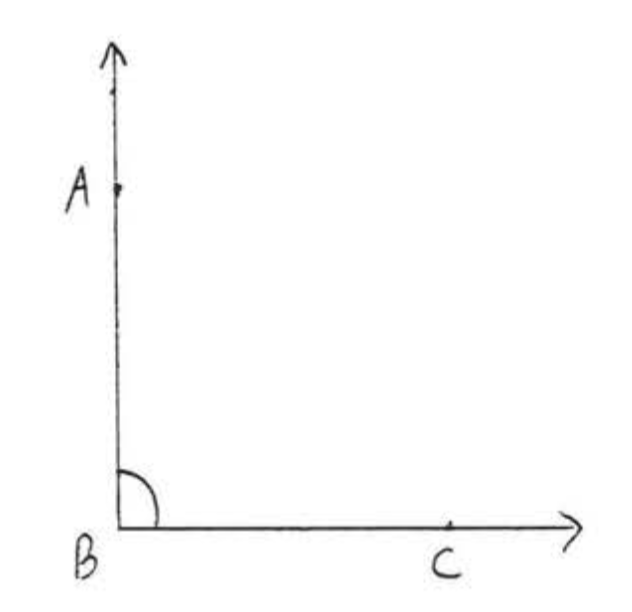
7 - 16, Виміряйте кожен із зазначених кутів:
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17 - 24. Намалюйте і позначте кожен кут:
17. \(\angle BAC = 30^{\circ}\)
18. \(\angle BAC = 40^{\circ}\)
19. \(\angle ABC = 45^{\circ}\)
20. \(\angle EFG = 60^{\circ}\)
21. \(\angle RST = 72^{\circ}\)
22. \(\angle XYZ = 90^{\circ}\)
23. \(\angle PQR = 135^{\circ}\)
24. \(\angle JKL = 164^{\circ}\)
25 - 28. Знайти,\(x\) якщо\(\overrightarrow{AC}\) бісекти\(\angle BAD\):
25. 
26. 
27. 
28. 
