16.5: Центральна проекція

Last updated
Save as PDF

Page ID: 59019

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Центральна проекція аналогічна проективній моделі гіперболічної площини, яка розглядається в главі 17.

$\Sigma$Дозволяти одиниця сфери з центром на початку, яка буде позначена$O$. Припустимо, що$\Pi^+$ позначає площину, визначену рівнянням$z=1$. Ця площина паралельна$xy$ -площині і вона проходить через північний полюс$N =(0,0,1)$$\Sigma$.

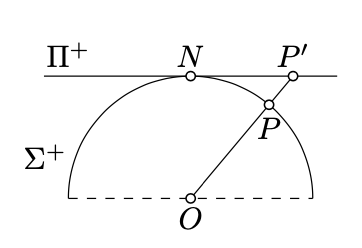
$2021-03-01 пнг$

Нагадаємо, що північна півкуля$\Sigma$, є підмножиною$(x,y,z)\in \Sigma$ таких точок, що$z>0$. Північна півкуля буде позначено символом$\Sigma^+$.

З огляду на$P\in \Sigma^+$ крапку, розглянемо напівлінію$[OP)$. Припустимо, що$P'$ позначає перетин$[OP)$ і$\Pi^+$. Зверніть увагу, що якщо$P=(x,y,z)$, то$P'=(\dfrac{x}{z},\dfrac{y}{z},1)$. Звідси випливає, що$P\leftrightarrow P'$ є біекцією між$\Sigma^+$ і$\Pi^+$.

Описувана біекція$\Sigma^+ \leftrightarrow \Pi^+$ називається центральною проекцією півкулі$\Sigma^+$.

Зверніть увагу, що центральна проекція посилає перетину великих$\Sigma^+$ кіл з лініями в$\Pi^+$. Останнє випливає, оскільки великі кола є перетинами$\Sigma$ з площинами, що проходять через початок, а також лінії в$\Pi^+$ перетині$\Pi^+$ з цими площинами.

Наступна вправа аналогічна вправу 17.2.1 в гіперболічній геометрії.

Вправа$\PageIndex{1}$

$\triangle_sABC$Дозволяти бути невиродженим сферичним трикутником. Припустимо,$\Pi^+$ що площина паралельна площині$A$, що проходить через$B$, і$C$. Нехай$A'$,$B'$, і$C'$ позначають центральні проекції$A$,$B$ і$C$.

Показати, що середні точки$[A'B']$$[B'C']$, і$[C'A']$ є центральними проекціями середніх точок$[AB]_s$$[BC]_s$, і$[CA]_s$ відповідно.
Використовуйте частину (a), щоб показати, що медіани сферичного трикутника перетинаються в одній точці.

Підказка

(а). Спостерігайте і використовуйте це$OA' = OB' = OC'$.

(б). Зауважимо, що медіани сферичного трикутника ABC відображають медіани Евклідова трикутника$A'B'C'$. Залишилося застосувати теорему 8.3.1 для$\triangle A'B'C'$.