16.3: Інверсія простору

Last updated
Save as PDF

Page ID: 59029

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Інверсія в сфері визначається так само, як ми визначаємо інверсію в колі.

Формально нехай$\Sigma$ буде сфера з центром$O$ і радіусом$r$. Інверсія в$\Sigma$ точці$P$ - це точка$P'\in[OP)$ така, що

$OP\cdot OP'=r^2.$

В цьому випадку сфера$\Sigma$ буде називатися сферою інверсії, а її центр - центром інверсії.

Ми також додаємо$\infty$ до простору і припускаємо, що центр інверсії$\infty$ відображений і навпаки. Простір$\mathbb{R}^3$ з точкою$\infty$ буде називатися інверсивним простором.

Інверсія простору має безліч властивостей інверсії площини. Найбільш важливими для нас є аналоги Теореми 10.2.1, Теореми 10.3.1 та Теореми 10.6.1, які можна узагальнити наступним чином:

Теорема$\PageIndex{1}$

Інверсія в сфері має такі властивості:

Інверсія відображає сферу або площину в сферу або площину.
Інверсія відображає коло або лінію в коло або лінію.
Інверсія зберігає перехресне співвідношення; тобто якщо$A'$,$B'$$C'$,, і$D'$ є оберненнями точок$A$$B$,$C$ і$D$ відповідно, то \[\dfrac{AB\cdot CD}{BC\cdot DA}= \dfrac{A'B'\cdot C'D'}{B'C'\cdot D'A'}.\]
Інверсія відображає дуги в дуги.
Інверсія зберігає абсолютне значення міри кута між дотичними півлініями до дуг.

Ми не представляємо тут доказів, але вони майже повторюють відповідні докази в геометрії площини. Щоб довести (а), вам знадобиться додатково наступна лема; її доказ залишається читачеві.

Лемма$\PageIndex{1}$

$\Sigma$Дозволяти підмножина евклідового простору, що містить принаймні дві точки. Закріпіть точку$O$ в просторі.

Тоді$\Sigma$ є сферою, якщо і тільки якщо для будь-якої площини$O$,$\Pi$ що проходить через, перетин$\Pi \cap \Sigma$ або порожній набір, один набір точок або коло.

Наступне спостереження допомагає зменшити частину (b) до частини (а).

Спостереження$\PageIndex{1}$

Будь-яке коло в просторі - це перетин двох сфер.

Визначимо круглий конус як набір, утворений відрізками лінії від нерухомої точки, званої кінчиком конуса, до всіх точок на нерухомому колі, званому підставою конуса; ми завжди припускаємо, що основа не лежить в тій же площині, що і кінчик. Ми говоримо, що конус правий, якщо центр базового кола є точкою ноги кінчика на базовій площині; інакше ми називаємо це косою.

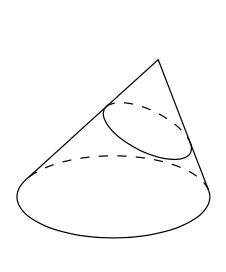
$2021-03-01 пнг$

Вправа$\PageIndex{1}$

$K$Дозволяти бути косою круглий конус. Покажіть, що існує площина$\Pi$, яка не паралельна базовій площині$K$ такої, що перетин$\Pi\cap K$ є колом.

Підказка: Розглянемо інверсію підстави в сфері з центром на кінчику конуса і застосуємо теорему$\PageIndex{1}$.

Теорема\(\PageIndex{1}\)

Лемма\(\PageIndex{1}\)

Спостереження\(\PageIndex{1}\)

Вправа\(\PageIndex{1}\)