16.4: Стереографічна проекція

Last updated
Save as PDF

Page ID: 59018

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

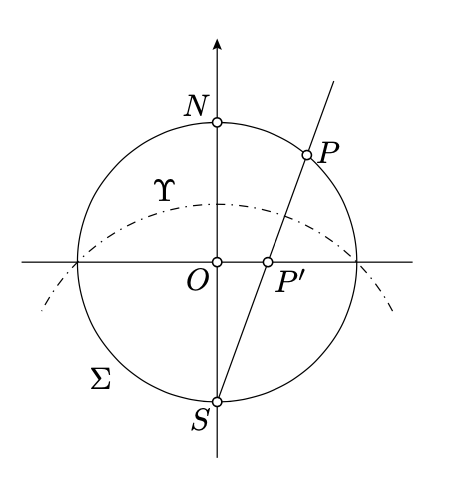
$2021-03-01 пнг$

Розглянемо одиничну сферу,$\Sigma$ зосереджену на початку$(0,0,0)$. Цю сферу можна описати рівнянням$x^2+y^2+z^2=1$.

Припустимо, що$\Pi$ позначає$xy$ -площину; вона визначається рівнянням$z = 0$. $\Pi$Зрозуміло, проходить через центр$\Sigma$.

Нехай$N = (0, 0, 1)$ і$S=(0, 0, -1)$ позначають «північний» і «південний» полюси$\Sigma$; це точки на сфері, які мають екстремальні відстані до$\Pi$. Припустимо, що$\Omega$ позначає «екватор»$\Sigma$; це перетин$\Sigma \cap \Pi$.

Для будь-якої точки$P\ne S$ на$\Sigma$, розгляньте лінію$(SP)$ в просторі. Ця лінія перетинається рівно$\Pi$ в одній точці, позначається символом$P'$. Набір$S'=\infty$.

Карта$\xi_s\: P\mapsto P'$ називається стереографічної проекцією від$\Sigma$ до$\Pi$ щодо південного полюса. Зворотна ця карта$\xi^{-1}_s\: P' \mapsto P$ називається стереографічною проекцією від$\Pi$ до по $\Sigma$відношенню до південного полюса.

Таким же чином можна визначити стереографічні проекції$\xi_n$ і$\xi^{-1}_n$ щодо північного полюса$N$.

Зверніть увагу, що$P=P'$ якщо і тільки якщо$P\in\Omega$.

Відзначимо, що якщо$\Sigma$ і$\Pi$ знаходяться як вище, то склад стереографічних проекцій$\xi_s: \Sigma\to\Pi$$\Sigma$ і$\xi^{-1}_s: \Pi\to\Sigma$ є обмеженнями до і$\Pi$ відповідно інверсії в сфері $\Upsilon$з центром$S$ і радіусом$\sqrt{2}$.

Зверху і теорема 16.3.1 випливає, що стереографічна проекція зберігає кути між дугами; точніше абсолютне значення міри кута між дугами на сфері.

Це робить його особливо корисним у картографії. Карту великої області землі неможливо зробити в постійному масштабі, але за допомогою стереографічної проекції можна зберегти кути між дорогами такими ж, як на землі.

У наступних вправах ми припускаємо, що$\Sigma$,,,$\Pi$,$\Upsilon$,,$\Omega$,$O$$S$, і$N$ є такими, як зазначено вище.

Вправа$\PageIndex{1}$

Показати$\xi_n \circ \xi^{-1}_s$, що, склад стереографічних проекцій$\Sigma$ від$\Pi$ до від$S$, а$\Pi$ від$\Sigma$ до$N$ - це зворотна площині$\Pi$ в$\Omega$.

Підказка

Зверніть увагу, що точки на$\Omega$ не рухаються. Крім того, точки всередині$\Omega$ відображаються зовні$\Omega$ і навпаки.

Далі зверніть увагу, що ця карта посилає кола на кола; крім того, перпендикулярні кола відображаються на перпендикулярних колах. Зокрема, кола,$\Omega$ перпендикулярні до них, нанесені на себе.

Розглянемо довільний момент$P \not\in \Omega$. Припустимо, що$P'$ позначає зворотне$P$ in$\Omega$. Виберіть два різних кола, які проходять через$P$ і$P'$. Згідно з Слідством 10.5.2,$\Gamma_1 \perp \Omega$ і$\Gamma_2 \perp \Omega$.

Тому зворотне в$\Omega$ посилає$\Gamma_1$ до себе і те ж саме тримає$\Gamma_2$.

Образ$P$ повинен лежати на$\Gamma_1$ і$\Gamma_2$. Оскільки образ$P$ відрізняється від$P$, ми отримуємо, що це повинно бути$P'$.

Вправа$\PageIndex{2}$

Показати, що стереографічна проекція$\Sigma\to\Pi$ посилає великі кола до плоских кіл, які перетинаються$\Omega$ в протилежних точках.

Підказка

Застосувати теорему 16.3.1 (b).

Наступна вправа аналогічно Леммі 13.5.1.

Вправа$\PageIndex{3}$

Закріпіть точку$P\in \Pi$ і нехай$Q$ буде ще одна точка в$\Pi$. Нехай$P'$ і$Q'$ позначають їх стереографічні проекції до$\Sigma$. Набір$x=PQ$ і$y=P'Q'_s$. Покажіть, що

$\lim_{x\to 0} \dfrac{y}{x}=\dfrac{2}{1+OP^2}.$

Підказка

Набір$z = P'Q'$. Зверніть увагу, що$\dfrac{y}{x} \to 1$ як$x \to 0$.

Залишилося показати, що

$\lim_{x \to 0} \dfrac{z}{x} = \dfrac{2}{OP^2}$

Нагадаємо, що стереографічна проекція - це інверсія в сфері$Upsilon$ з центром на південному полюсі,$S$ обмеженим площиною$\Pi$. Покажіть, що є літак, що$\Lambda$ проходить через$S, P, Q, P'$, і$Q'$. У площині$\Lambda$ карта$Q \mapsto Q'$ є інверсією в колі$\Upsilon \cap \Lambda$.

Це зводить задачу до евклідової геометрії площини. Решта розрахунків в$\Lambda$ аналогічні тим, що наведені в доказі Lemma 13.5.1.

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)

Вправа\(\PageIndex{3}\)