16.2: Теорема Піфагора

Last updated
Save as PDF

Page ID: 59024

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Ось аналог теорем Піфагора (Теорема 6.2.1 і Теорема 13.. 1) в сферичній геометрії.

Теорема$\PageIndex{1}$ Spherical Pythagorean Theorem

$\triangle_sABC$Дозволяти сферичний трикутник з прямим кутом в$C$. Набір$a=BC_s$,$b=CA_s$, і$c=AB_s$. Тоді

$\cos c=\cos a \cdot \cos b.$

Доказ

Так як кут в$C$ правильному, ми можемо вибрати координати в$\mathbb{R}^3$ так$v_C\z=(0,0,1)$, що,$v_A$ лежить в$xz$ -площині, так$v_A=(x_A,0,z_A)$, і$v_B$ лежить в$yz$ -площині, так $v_B=(0,y_B,z_B)$.

Застосовуючи, 16.2.3, ми отримуємо, що

$\begin{aligned} z_A&=\langle v_C,v_A\rangle =\cos b, \\ z_B&=\langle v_C,v_B\rangle =\cos a.\end{aligned}$

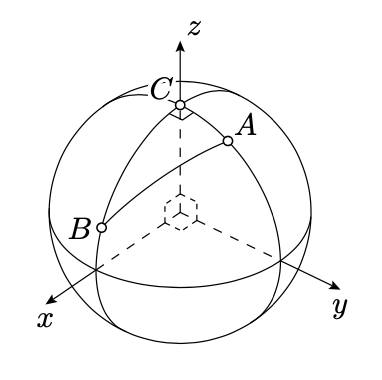
$2021-02-26 пнг$

Застосовуючи, 16.2.1 та 16.2.3, ми отримуємо, що

$\begin{aligned} \cos c &=\langle v_A,v_B\rangle= \\ &=x_A\cdot 0+0\cdot y_B+z_A\cdot z_B= \\ &=\cos b\cdot\cos a.\end{aligned}$

На доказ ми будемо використовувати поняття скалярного добутку, який ми збираємося обговорити.

Нехай$v_A=(x_A,y_A,z_A)$ і$v_B=(x_B,y_B,z_B)$ позначають вектори положення точок$A$ і$B$. Скалярний добуток двох векторів$v_A$ і$v_B$$\mathbb{R}^3$ in визначається як

\[\langle v_A,v_B\rangle := x_A\cdot x_B+y_A\cdot y_B+z_A\cdot z_B.\]

Припустимо, що обидва вектори$v_A$ і$v_B$ є ненульовими; припустимо, що$\phi$ позначає міру кута між ними. Тоді скалярний добуток можна виразити наступним чином:

\[\langle v_A,v_B\rangle=|v_A|\cdot|v_B|\cdot\cos\phi, \]

де

$\begin{aligned} |v_A|&=\sqrt{x_A^2+y_A^2+z_A^2}, & |v_B|&=\sqrt{x_B^2+y_B^2+z_B^2}.\end{aligned}$

Тепер припустимо, що точки$A$ і$B$ лежать на одиниці сфери$\Sigma$ в$\mathbb{R}^3$ центрі на початку. В даному випадку$|v_A|=|v_B|=1$. До 16.2.2 ми отримуємо це

\[\cos AB_s=\langle v_A,v_B\rangle.\]

Вправа$\PageIndex{1}$

Показати, що якщо$\triangle_s ABC$ це сферичний трикутник з прямим кутом в$C$, і$AC_s=BC_s=\dfrac{\pi}{4}$, то$AB_s=\dfrac{\pi}{3}$.

Підказка

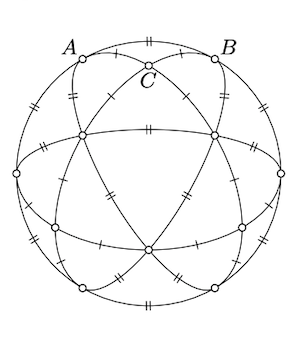
$2021-02-26 пнг$

Застосовуючи теорему Піфагора, отримаємо, що

$\cos AB_s = \cos AC_s \cdot \cos BC_s = \dfrac{1}{2}.$

Тому$AB_s = \dfrac{\pi}{3}.$

Крім того, подивіться на тесселяцію півкулі на малюнку; вона зроблена з 12 копій$\triangle_s ABC$ і ще 4 рівносторонніх сферичних трикутників. З симетрії цієї тесселяції випливає, що$[AB]_s$ займає$\dfrac{1}{6}$ екватор; тобто$AB_s = \dfrac{\pi}{3}$.