5.3: Унікальність перпендикуляра

Last updated
Save as PDF

Page ID: 59223

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Теорема$\PageIndex{1}$

Існує одна і тільки одна лінія, яка проходить через задану точку$P$ і перпендикулярна до даної лінії$\ell$.

Згідно з вищевказаною теоремою, є унікальний момент$Q \in \ell$ такий, що$(QP) \perp \ell$. Ця точка$Q$ називається точкою стопи$P$ на$\ell$.

Доказ

Якщо$P \in \ell$, то і існування, і унікальність випливають з Аксіоми III.

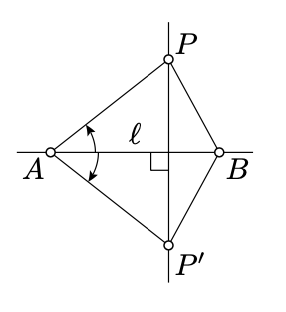
$2021-02-04 пнг$

Існування для$P \not\in \ell$. $A$$B$Дозволяти і бути двома різними точками$\ell$. Вибирайте$P'$ так, щоб$AP' = AP$ і$\meauredangle BAP' \equiv - \measuredangle BAP$. Відповідно до Аксіоми IV,$\triangle AP'B \cong \triangle APB$. Зокрема,$AP = AP'$ і$BP = BP'$.

Відповідно до теореми 5.2.1,$A$ і$B$ лежать на перпендикулярній бісектрисі до$[PP']$. Зокрема,$(PP') \perp (AB) = \ell$.

Унікальність для$P \not\in \ell$. Зверху ми можемо вибрати точку таким$P'$ чином, що$\ell$ утворює перпендикулярну бісектрису до$[PP']$.

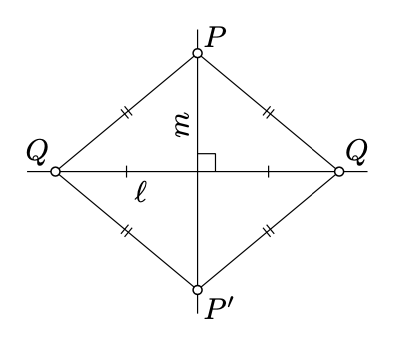
$2021-02-04 пнг$

Припустимо$m \perp \ell$ і$P \in m$. Потім$m$ йде перпендикулярна бісектриса до якогось$[QQ']$ сегмента$\ell$; зокрема,$PQ = PQ'$.

Так як$\ell$ перпендикулярна бісектриса до$[PP']$, ми отримуємо що$PQ = P'Q$ і$PQ' = P'Q'$. Тому,

$P'Q = PQ = PQ' = P'Q'$.

За теоремою 5.2.1,$P'$ лежить на перпендикулярній бісектрисі до$[QQ']$, який є$m$. За аксіомою II,$m = (PP')$.