5.2: Перпендикулярна бісектриса

Last updated
Save as PDF

Page ID: 59237

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Припустимо,$M$ це середина сегмента$[AB]$; тобто$M \in (AB)$ і$AM = MB$.

Лінія$\ell$, яка проходить через$M$ і перпендикулярна до$(AB)$, називається перпендикулярної бісектриси до відрізка$[AB]$.

Теорема$\PageIndex{1}$

З огляду на різні точки$A$ і$B$, всі точки рівновіддалені від$A$$B$ і ніякі інші лежать на перпендикулярній бісектрисі до$[AB]$.

Доказ

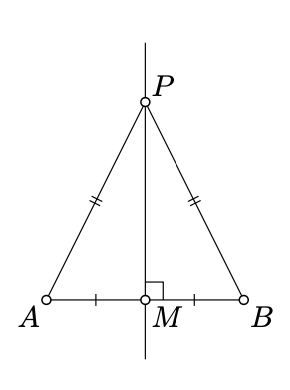
$2021-02-03 пнг$

$M$Дозволяти бути серединою$[AB]$.

Припустимо$PA = PB$ і$P \ne M$. Згідно ССС (теорема 4.4.1),$\triangle AMP \cong \triangle BMP$. Звідси

$\measuredangle AMP = \pm \measuredangle BMP.$

Так як$A \ne B$, у нас є «-» в наведеній вище формулі. Далі,

\[\begin{array} {rcl} {\pi} & = & {\measuredangle AMB \equiv} \\ {} & \equiv & {\measuredangle AMP + \measuredangle PMB \equiv} \\ {} & \equiv & {2 \cdot \measuredangle AMP.} \end{array}\]

Тобто,$\measuredangle AMP = \pm \dfrac{\pi}{2}$. Тому$P$ лежить на перпендикулярній бісектрисі.

Щоб довести зворотне, припустимо,$P$ що будь-яка точка на перпендикулярній бісектрисі до$[AB]$ і$P \ne M$. Потім$\measuredangle AMP = \pm \dfrac{\pi}{2}$,$\measuredangle BMP = \pm \dfrac{\pi}{2}$ і$AM = BM$. За SAS,$\triangle AMP \cong \triangle BMP$; зокрема,$AP = BP$.

Вправа$\PageIndex{1}$

$\ell$Дозволяти бути перпендикулярна бісектриса до відрізка$[AB]$ і$X$ бути довільною точкою на площині.

Покажіть, що$AX < BX$ якщо і тільки якщо$X$ і$A$ лежати на одній стороні від$\ell$.

Підказка

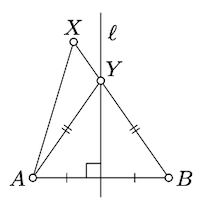
$2021-02-03 пнг$

$X$Припускаємо і$A$ лягаємо на одну сторону$\ell$.

Зверніть увагу, що$A$ і$B$ ляжте на протилежну сторону від$\ell$. Тому, за слідством 3.4.1,$[AX]$ не перетинається$\ell$ і$[BX]$ не перетинається$\ell$; припустимо, що$Y$ позначає точку перетину.

Зауважте, що$BX = AY + YX \ge AX$. Так як$X \not\in \ell$, за теоремою$\PageIndex{1}$ ми маємо$BX \ne BA$. Тому$BX > AX$.

Таким чином ми довели частину «якщо». Щоб довести частину «тільки якщо», потрібно переключитися$A$ і$B$ і повторити вищевказаний аргумент.

Вправа$\PageIndex{2}$

$ABC$Дозволяти бути невиродженим трикутником. Покажіть, що

$AC > BC \Leftrightarrow |\measuredangle ABC| > |\measuredangle CAB|.$

Підказка: Застосовуйте вправу$\PageIndex{1}$, теорему 4.2.1 та вправу 3.1.2.

Теорема\(\PageIndex{1}\)

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)