5.5: Перпендикуляр найкоротший

Last updated
Save as PDF

Page ID: 59236

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Лемма$\PageIndex{1}$

Припустимо,$Q$ це точка стопи$P$ на лінії$\ell$. Тоді нерівність

$PX > PQ$

тримає для будь-якої точки$X$ на$\ell$ відмінному від$Q$.

Якщо$P, Q$, і$\ell$ знаходяться як вище, то$PQ$ називається відстань від$P$ до$\ell$.

Доказ

Якщо$P \in \ell$, то результат випливає з$PQ = 0$. Далі припускаємо, що$P \not\in \ell$.

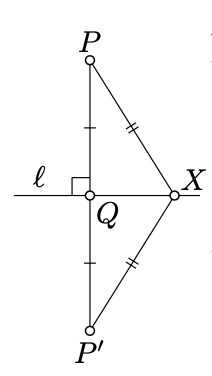
$2021-02-04 пнг$

$P'$Дозволяти відображенням$P$ через лінію$\ell$. Зверніть увагу, що$Q$ це середина$[PP']$ і$\ell$ є перпендикулярною бісектрисою$[PP']$. Тому

$PX = P'X$і$PQ = P'Q = \dfrac{1}{2} \cdot PP'$

Зверніть увагу, що$\ell$ зустрічається$[PP']$ тільки в точці$Q$. Отже,$X \not\in [PP']$; нерівністю трикутника та наслідком 4.4.1,

$PX + P'X > PP'$

а звідси і результат:$PX > PQ$.

Вправа$\PageIndex{1}$

Припустимо$\angle ABC$, є правильним або тупим. Покажіть, що

$AC > AB.$

Підказка

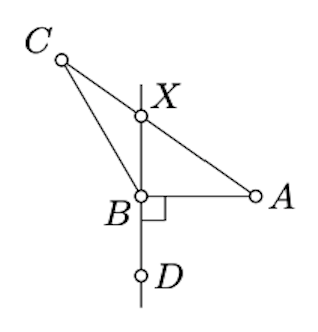
$2021-02-04 пнг$

Якщо$\angle ABC$ правильно, твердження випливає з Лемми$\PageIndex{1}$. Тому можна припустити, що$\angle ABC$ це тупий.

Намалюйте лінію$(BD)$ перпендикулярно до$(BA)$. Так$\angle ABC$ як тупий, то кути$DBC$ мають$DBA$ і протилежні знаки.

За наслідком 3.4.1,$A$ і$C$ лежить на протилежних сторонам$(BD)$. Зокрема,$[AC]$ перетинається$(BD)$ в точці; позначають його по$X$.

Зауважте, що$AX < AC$ і Лемма$\PageIndex{1}$,$AB \le AX$.

Вправа$\PageIndex{2}$

Припустимо, що$\triangle ABC$ має прямий кут на$C$. Покажіть, що для будь-якого$X \in [AC]$ відстань$(AB)$ від$X$ до менше$AB$.

Підказка

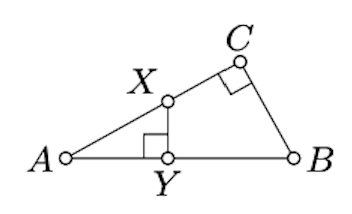
$2021-02-04 1.54.06png$

$Y$Дозволяти бути точкою стопи$X$ на$(AB)$. Застосуйте Lemma$\PageIndex{1}$, щоб показати, що$XY < AX \le AC < AB$.

Лемма\(\PageIndex{1}\)

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)