5.6: Кола

Last updated
Save as PDF

Page ID: 59230

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Нагадаємо, що коло з радіусом$r$ і центром$O$ - це сукупність всіх точок на відстані$r$ від$O$. Ми говоримо, що точка$P$ лежить всередині кола, якщо$OP < r$; якщо$OP > r$, ми говоримо, що$P$ лежить за межами кола.

Вправа$\PageIndex{1}$

$\Gamma$Дозволяти буде коло і$P \not\in \Gamma$. Припустимо$\ell$, що лінія проходить через точку$P$ і перетинається$\Gamma$ в двох різних точках,$X$ і$Y$. Покажіть, що$P$ знаходиться всередині,$\Gamma$ якщо і тільки якщо$P$ лежить між$X$ і$Y$.

Підказка

$O$Дозволяти бути центром кола. Зверніть увагу, що ми можемо припустити, що$O \ne P$.

Припустимо,$P$ лежить між$X$ і$Y$. За вправою 5.1.1 можна вважати, що$OPX$ є правильним або тупим. За вправою 5.5.1,$OP < OX$; тобто$P$ лежить всередині$\Gamma$.

Якщо$P$ не лежить між$X$ і$Y$, можна припустити, що$X$ лежить між$P$ і$Y$. Оскільки$OX = OY$, Вправа 5.5.1 має на увазі, що$\angle OXY$ є гострим. Тому$\angle OXP$ тупий. Застосовуючи Вправу 5.5.1 знову отримуємо, що$OP > OX$ л тобто$P$ лежить зовні$\Gamma$.

Відрізок між двома точками на колі називається хордою кола. Хорда, що проходить через центр кола, називається її діаметром.

Вправа$\PageIndex{2}$

Припустимо два різних кола$\Gamma$ і$\Gamma'$ мають спільний акорд$[AB]$. Показати, що лінія між центрами$\Gamma$ і$\Gamma'$ утворює перпендикулярну бісектрису до$[AB]$.

Підказка: Застосувати теорему 5.2.1.

Лемма$\PageIndex{1}$

Лінія і коло можуть мати не більше двох точок перетину.

Доказ

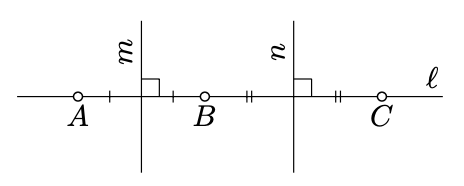
$2021-02-04 пнг$

Припустимо$A, B$, і$C$ є окремими точками, які лежать на лінії$\ell$ і коло$\Gamma$ з центром$O$. Потім$OA = OB = OC$; зокрема,$O$ лежить на перпендикулярних$m$ бісектрисах і$n$ до$[AB]$ і$[BC]$ відповідно. Зверніть увагу, що середні точки$[AB]$ і$[BC]$ є різними. Тому$m$ і$n$ відрізняються. Суперечить єдиності перпендикуляра (теорема 5.3.1).

Вправа$\PageIndex{3}$

Показати, що два різних кола можуть мати не більше двох точок перетину.

Підказка: Використовуйте вправу$\PageIndex{2}$ і теорему 5.3.1.

Внаслідок вищезазначеної леми лінія$\ell$ і коло$\Gamma$ можуть мати 2, 1 або 0 точок перетину. У першому випадку лінія називається січною лінією, у другому - дотичною лінією; якщо$P$ є єдиною точкою перетину$\ell$ і$\Gamma$, ми говоримо,$\ell$ що дотична до$\Gamma$ at$P$.

Аналогічно, згідно з Вправою$\PageIndex{3}$, два різних кола можуть мати 2, 1 або 0 точок перетину. Якщо$P$ є єдиною точкою перетину кіл$\Gamma$ і$\Gamma'$, ми говоримо, що$\Gamma$ є дотичною до$\Gamma$ at$P$; ми також припускаємо, що коло є дотичною до себе в будь-якій його точці.

Лемма$\PageIndex{2}$

$\ell$Дозволяти бути лінією і$\Gamma$ бути коло з центром$O$. Припустимо,$P$ це загальна точка$\ell$ і$\Gamma$. Потім$\ell$ дотична до$\Gamma$ at$P$ якщо і тільки якщо$(PQ) \perp \ell$.

Доказ

$Q$Дозволяти бути точкою стопи$O$ на$\ell$.

Припустимо$P \ne Q$. Нехай$P'$ буде відображенням$P$ поперек$(OQ)$. Зверніть увагу, що$P' \in \ell$ і$(OQ)$ є перпендикулярною бісектрисою$[PP']$. Тому,$OP = OP'$. Отже$P, P' \in \Gamma \cap \ell$; тобто$\ell$ є секантним до$\Gamma$.

Якщо$P = Q$, то відповідно до Лемма 5.5.1,$OP < OX$ для будь-якої точки$X \in \ell$ відмінною від$P$. Звідси$P$ є єдиною точкою на перетині$\Gamma \cap \ell$;$\ell$ тобто дотична до$\Gamma$ at$P$.

Вправа$\PageIndex{4}$

$\Gamma$$\Gamma'$Дозволяти і бути два різних кола з центрами в$O$ і$O'$ відповідно. Припустимо,$\Gamma$ зустрічається$\Gamma'$ в точці$P$. Показати,$\Gamma$ що дотично до$\Gamma'$ якщо і тільки якщо$O$$O'$, і$P$ лежати на одному рядку.

Підказка: Нехай$P'$ буде відображенням$P$ поперек$(OO')$. Зверніть увагу, що$P'$ лежить на обох колах і$P' \ne P$ якщо і тільки якщо$P \not\in (OO')$.

Вправа$\PageIndex{5}$

$\Gamma$$\Gamma'$Дозволяти і бути два різних кола з центрами в$O$ і$O'$ і радіуси$r$ і$r'$. Показати,$\Gamma$ що дотично до$\Gamma'$ якщо і тільки якщо

$OO' = r + r'$або$OO' = |r - r'|$.

Підказка: Застосувати вправу$\PageIndex{4}$

Вправа$\PageIndex{6}$

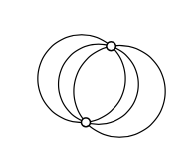
Припустимо, три кола мають дві спільні точки. Доведіть, що їх центри лежать на одній лінії.

$2021-02-04 пнг$

Підказка: $A$$B$Дозволяти і бути точками перетину. Зверніть увагу, що центри лежать на перпендикулярній бісектрисі відрізка$[AB]$.

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)

Лемма\(\PageIndex{1}\)

Вправа\(\PageIndex{3}\)

Лемма\(\PageIndex{2}\)

Вправа\(\PageIndex{4}\)

Вправа\(\PageIndex{5}\)

Вправа\(\PageIndex{6}\)