11.10: Розв'язування задачі Діріхле для гармонійних функцій

Last updated
Save as PDF

Page ID: 62834

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Загалом, задача Діріхле в області$A$ просить вас розв'язати рівняння з частинними похідними,$A$ де$A$ задаються значення розв'язку на межі.

Приклад$\PageIndex{1}$

Знайдіть$u$ гармоніку функції на одиничному диску таку, що

\[u(e^{i \theta}) = \begin{cases} 1 & \text{ for } 0 < \theta < \pi \\ 0 & \text{ for } -\pi < \theta < 0 \end{cases}\]

Це задача Діріхле, оскільки вказані значення$u$ на межі. Рівняння з частинними похідними мається на увазі, що вимагає, щоб$u$ бути гармонійним, тобто ми вимагаємо$\nabla ^2 u = 0$. Ми вирішимо цю проблему з часом.

Гармонічні функції на верхній півплощині

Наша стратегія полягатиме у вирішенні задачі Діріхле для гармонійних функцій на верхній півплощині, а потім перенесення цих розв'язків в інші області.

Приклад$\PageIndex{2}$

Знайти гармонійну функцію$u(x, y)$ на верхній півплощині, яка задовольняє граничній умові

\[u(x, 0) = \begin{cases} 1 & \text{ for } x < 0 \\ 0 & \text{ for } x > 0 \end{cases}\]

Рішення

Ми можемо записати рішення явно як

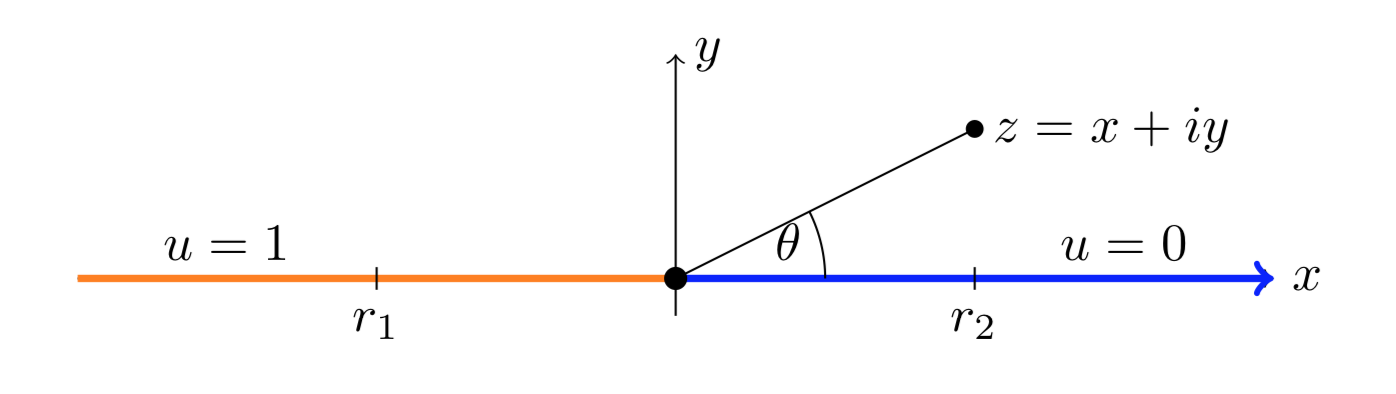
\[u(x, y) = \dfrac{1}{\pi} \theta,\]

$\theta$де аргумент$z = x + iy$. Оскільки ми працюємо лише над верхньою півплощиною, ми можемо взяти будь-яку зручну гілку з гілкою, зрізаною в нижній півплощині, скажімо$-\pi /2 < \theta < 3 \pi /2$.

$2020-09-14 1.15.00.png$

Щоб показати$u$ це справді рішення, ми повинні перевірити дві речі:

$u$задовольняє граничним умовам
$u$гармонійний.

Обидва вони прості. Спочатку подивіться на точку$r_2$ на позитивній$x$ -осі. Це має аргумент$\theta = 0$, так що$u(r_2, 0) = 0$. Так само$\text{arg} (r_1) = \pi$, так$u(r_1, 0) = 1$. Таким чином, ми показали точку (1).

Щоб побачити точку (2) пам'ятайте, що

\[\log (z) = \log (r) + i \theta.\]

Отже,

\[u = \text{Re} (\dfrac{1}{\pi i} \log (z)).\]

Оскільки вона є реальною частиною аналітичної функції,$u$ є гармонійною.

Приклад$\PageIndex{3}$

Припустимо$x_1 < x_2 < x_3$. Знайти гармонійну функцію$u$ на верхній півплощині, яка задовольняє граничній умові

\[u(x, 0) = \begin{cases} c_0 & \text{ for } x < x_1 \\ c_1 & \text{ for } x_1 < x < x_2 \\ c_2 & \text{ for } x_2 < x < x_3 \\ c_3 & \text{ for } x_3 < x \end{cases}\]

Рішення

Імітуємо попередній приклад і записуємо рішення

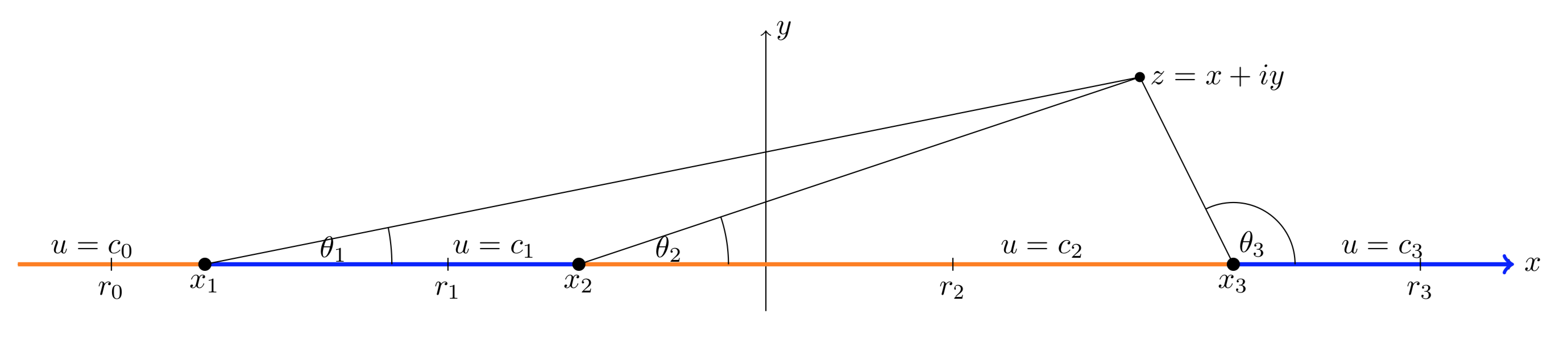
\[u(x, y) = c_3 + (c_2 - c_3) \dfrac{\theta_3}{\pi} + (c_1 - c_2) \dfrac{\theta_2}{\pi} + (c_0 - c_1) \dfrac{\theta_1}{\pi}.\]

Ось кути$\theta_j$, показані на малюнку. Знову ж таки, ми вибрали гілку$\theta$, яка має$0 < \theta < \pi$ для точок у верхній половині площини. (Наприклад, гілка$-\pi /2 < \theta < 3\pi /2$.)

$2020-09-14 1.25.33.PNG$

Щоб переконати себе, що$u$ задовольняє гранична умова тест кілька моментів:

За адресою$r_3$: все$\theta_j = 0$. Отже,$u(r_3, 0) = c_3$ в міру необхідності.
За адресою$r_2$:$\theta_1 = \theta_2 = 0$,$\theta_3 = \pi$. Отже,$u(r_2, 0) = c_3 + c_2 - c_3 = c_2$ в міру необхідності.
Аналогічно, в$r_1$ і$r_0$,$u$ мають правильні значення.

Як і раніше,$u$ є гармонійним, оскільки це реальна частина аналітичної функції

\[\Phi (z) = c_3 + \dfrac{(c_2 - c_3)}{\pi i} \log (z - x_3) + \dfrac{(c_1 - c_2)}{\pi i} \log (z - x_2) + \dfrac{(c_1 - c_0)}{\pi i} \log (z - x_1).\]

Гармонічні функції на одиничному диску

Спробуємо вирішити проблему, подібну до тієї, що в прикладі 11.9.1..

Приклад$\PageIndex{4}$

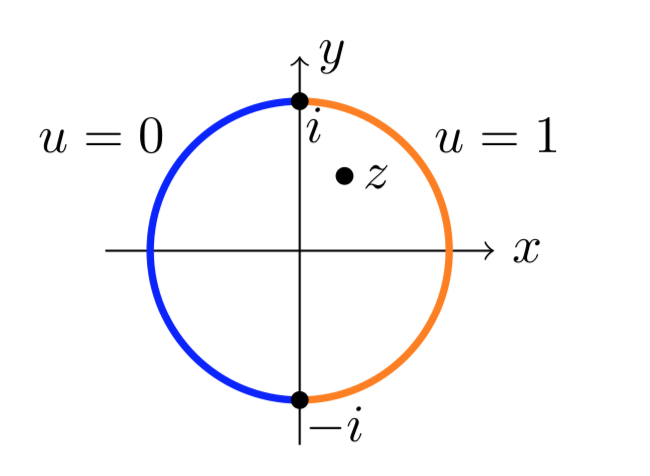
Знайдіть$u$ гармоніку функції на одиничному диску таку, що

\[u (e^{i \theta}) = \begin{cases} 1 & \text{ for } -\pi /2 < \theta < \pi /2 \\ 0 & \text{ for } \pi /2 < \theta < 3\pi /2 \end{cases}\]

$2020-09-14 1.34.35.png$

Рішення

Наша стратегія полягає в тому, щоб почати з конформної карти$T$ від верхньої півплощини до одиничного диска. Ми можемо використовувати цю карту, щоб повернути проблему назад до верхньої півплощини. Вирішуємо її там і потім штовхаємо розчин назад на диск.

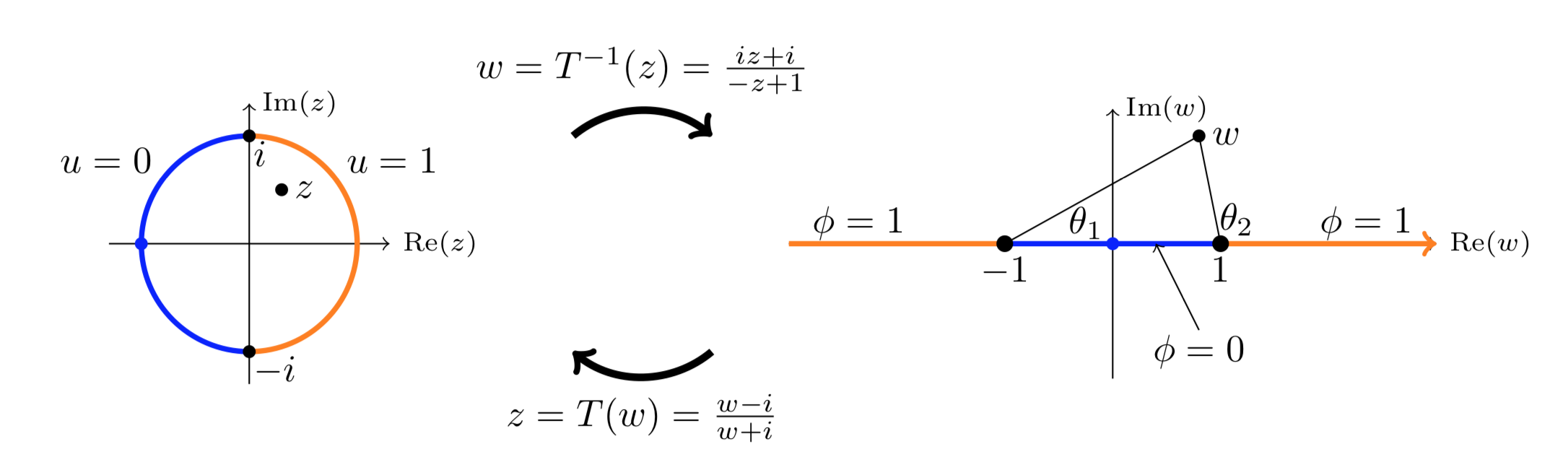
Назвемо диск$D$, верхню півплощину$H$. $z$Дозволяти бути змінна$w$ на$D$ і змінна на$H$. Повернувшись у прикладі 11.7.4 ми знайшли карту від$H$ до$D$. Карта та її зворотна

\[z = T(w) = \dfrac{w - i}{w + i}, \ \ \ \ \ \ \ \ w = T^{-1} (z) = \dfrac{iz + i}{-z + 1}.\]

$2020-09-14 1.39.16.png$

Функція$u$$D$ увімкнено перетворюється$T$ на функцію$\phi$ увімкнено$H$. Відносини є

\[u(z) = \phi \circ T^{-1} (z)\ \ \ \ \ \ \ \ \text{or} \ \ \ \ \ \ \ \ \phi (w) = u \circ T(w)\]

Ці відносини визначають граничні значення$\phi$ від тих, для яких нам дали$u$. Обчислюємо:

$T^{-1} (i) = -1$,$T^{-1} (-i) = 1$,$T^{-1} (1) = \infty$,$T^{-1} (-1) = 0$.

Це показує, що ліве півколо$D$ обмежує відображення відрізка [-1, 1] на дійсній осі. Так само півколо правої руки відображає дві показані напівлінії. (Буквально, до «сегмента» від 1$\infty$ до -1.)

Ми знаємо, як вирішити задачу для гармонійної функції$\phi$ на$H$:

\[\phi (w) = 1 - \dfrac{1}{\pi} \theta _2 + \dfrac{1}{\pi} \theta _1 = \text{Re} (1 - \dfrac{1}{\pi i} \log (w - 1) + \dfrac{1}{\pi i} \log (w + 1)).\]

Перетворення цього назад на диск, який ми маємо

\[u(z) = \phi \circ T^{-1} (z) = \text{Re} (1 - \dfrac{1}{\pi i} \log (T^{-1} (z) - 1) + \dfrac{1}{\pi i} \log (T^{-1} (z) + 1)).\]

Якби ми хотіли, ми могли б дещо спростити це, використовуючи формулу для$T^{-1}$.

Приклад\(\PageIndex{2}\)

Приклад\(\PageIndex{3}\)

Приклад\(\PageIndex{4}\)

Приклад\(\PageIndex{1}\)

Гармонічні функції на верхній півплощині

Приклад\(\PageIndex{2}\)

Приклад\(\PageIndex{3}\)

Гармонічні функції на одиничному диску

Приклад\(\PageIndex{4}\)