6.6: Ортогональність кривих

Last updated
Save as PDF

Page ID: 62600

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Важливою властивістю гармонійних$u$ сполучень і$v$ є те, що їх криві рівня ортогональні. Ми починаємо з показу їх градієнтів ортогональні.

Лемма$\PageIndex{1}$

Нехай$z = x + iy$ і припустимо, що$f(z) = u(x, y) + iv(x, y)$ це аналітично. Тоді точковий добуток їх градієнтів дорівнює 0, тобто

\[\Delta u \cdot \Delta v = 0.\]

Доказ

Доказом є легке застосування рівнянь Коші - Рімана.

\[\Delta u \cdot \Delta v = (u_x, u_y) \cdot (v_x, v_y) = u_x v_x + u_y v_y = v_y v_x - v_x v_y = 0\]

На останньому кроці ми використовували рівняння Коші - Рімана$v_y$ для заміни$u_x$ і$-v_x$ для$u_y$.

Лема тримає, чи градієнти 0. Щоб гарантувати, що криві рівня є гладкими, наступна теорема вимагає цього$f'(z) \ne 0$.

Теорема$\PageIndex{1}$

Нехай$z = x + iy$ і припустимо, що

\[f(z) = u(x, y) + iv(x, y)\]

є аналітичним. Якщо$f'(z) \ne 0$ тоді крива рівня$u$$(x, y)$ наскрізного ортогональна кривій рівня$v$ через$(x, y)$.

Доказ

Технічна вимога, яка$f'(z) \ne 0$ необхідна для того, щоб переконатися, що криві рівня плавні. Нам потрібна плавність, щоб навіть було сенс запитати, чи є криві ортогональними. Про це ми розповімо нижче. Припускаючи, що криві гладкі, доказ теореми є тривіальним: з 18.02 ми знаємо, що градієнт$\nabla u$ ортогональний кривим рівня$u$ і те саме вірно для$\nabla v$ кривих рівня$v$. Оскільки за Lemma 6.6.1 градієнти ортогональні, це означає, що криві ортогональні.

Нарешті, ми показуємо,$f'(z) \ne 0$ що криві є гладкими. Спочатку зауважте, що

\[f'(z) = u_x(x, y) - iu_y (x, y) = v_y (x, y) + iv_x (x, y).\]

Тепер, оскільки$f'(z) \ne 0$ ми знаємо, що

\[\nabla u = (u_x, u_y) \ne 0.\]

Так само,$\nabla v \ne 0$. Таким чином, градієнти не дорівнюють нулю, а криві рівня повинні бути плавними.

Приклад$\PageIndex{1}$

На малюнках нижче показані криві рівня$u$ і$v$ для ряду функцій. У всіх випадках криві рівня помаранчевого кольору, а$u$ криві рівня$v$ синього кольору. Для кожного випадку ми показуємо криві рівня окремо, а потім накладаємо один на одного.

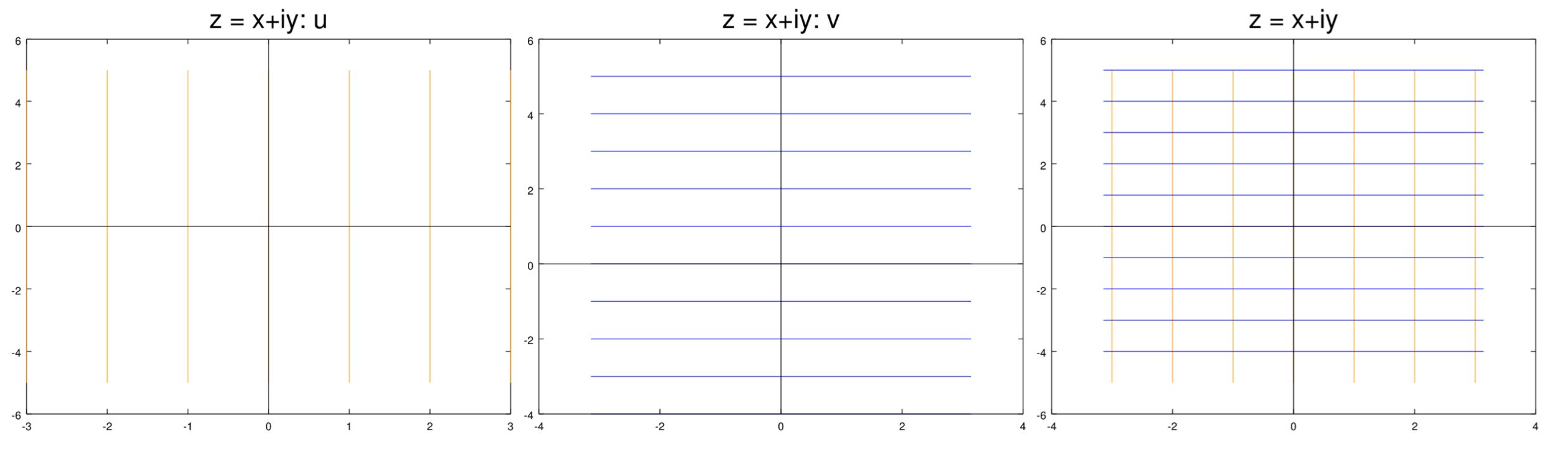
$2020-09-09 пнг$

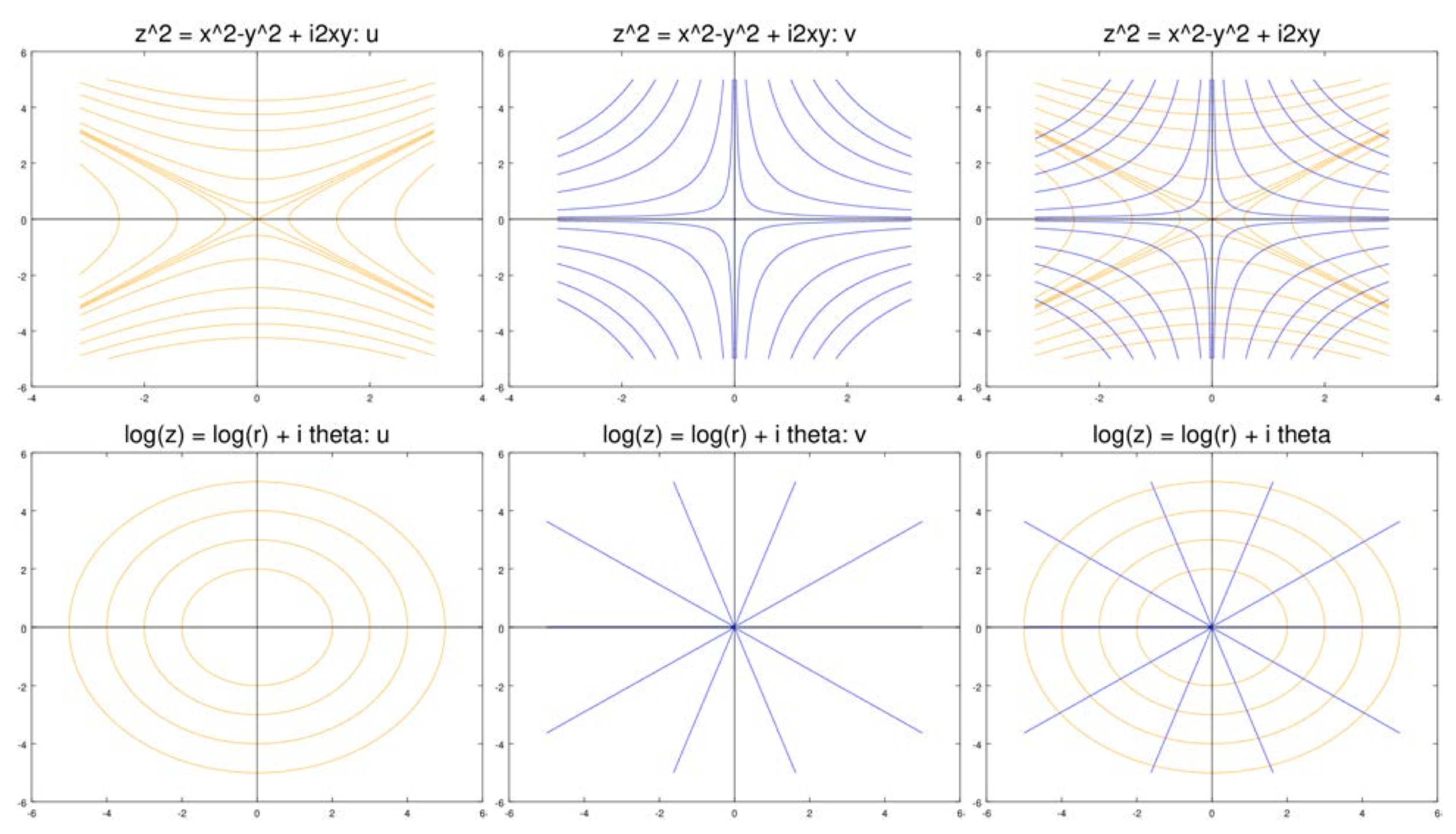
$2020-09-09 12.39.55.png$

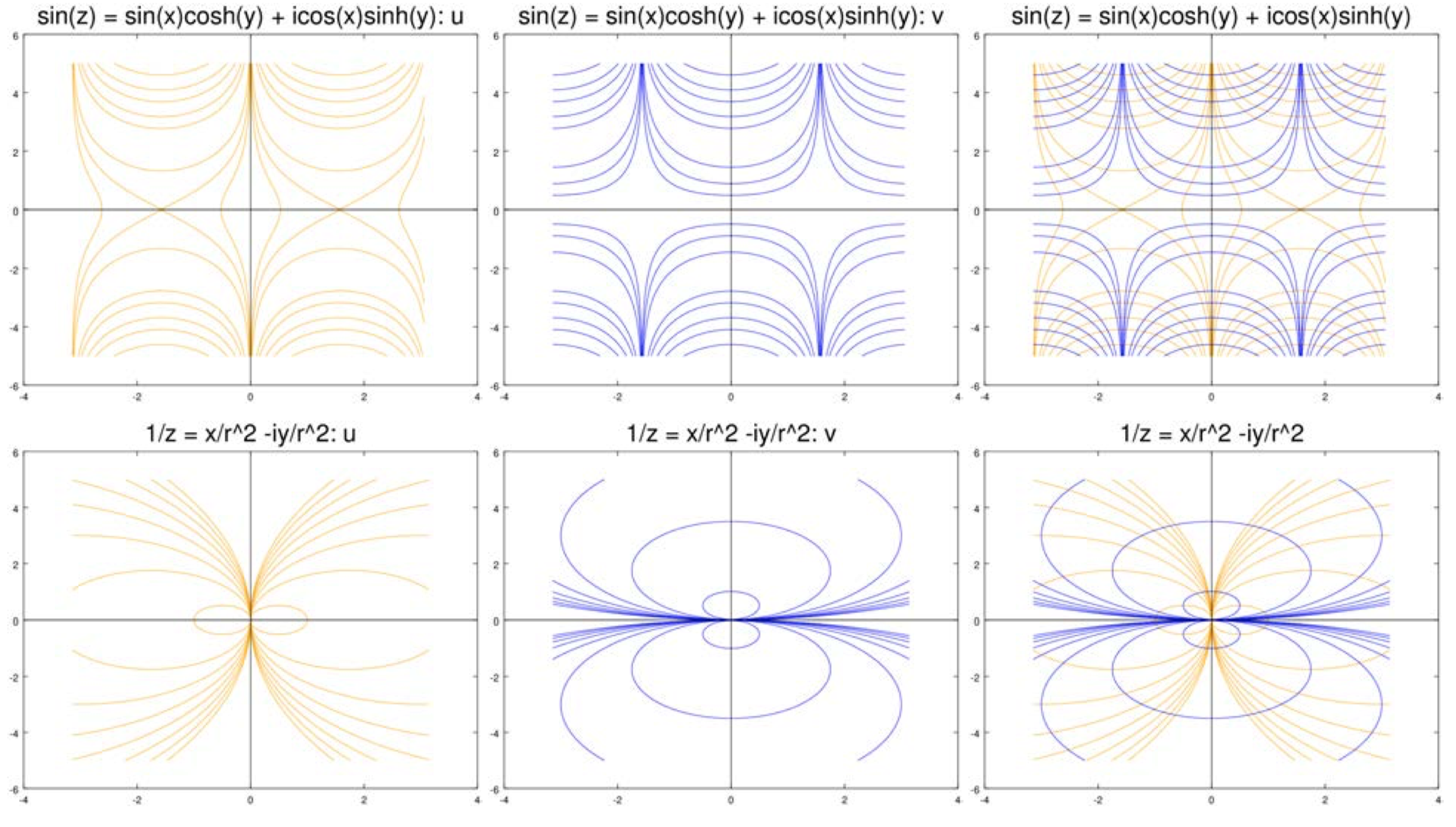
$2020-09-09 12.40.32.png$

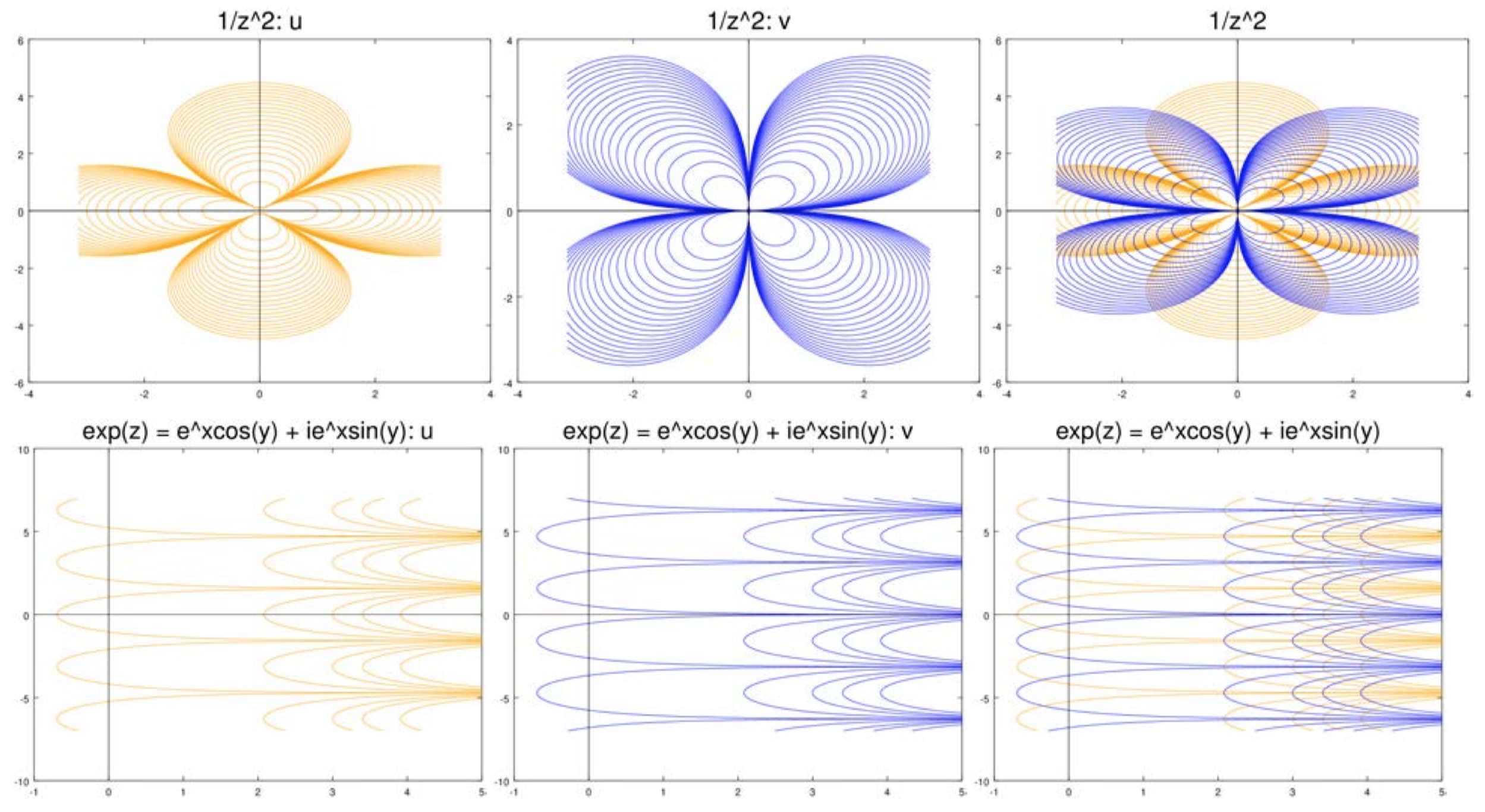
$2020-09-09 пнг$

$2020-09-09 1.46.35.png$

Приклад$\PageIndex{2}$

(i) Нехай

\[f(z) = z^2 = (x^2 - y^2) + i2xy,\]

Так

\[\nabla u = (2x, -2y) \text{ and } \nabla v = (2y, 2x).\]

Це тривіально$\nabla u \cdot \nabla v = 0$, щоб перевірити це, тому вони ортогональні.

(ii) Нехай

\[f(z) = \dfrac{1}{z} = \dfrac{x}{r^2} - i \dfrac{y}{r^2}.\]

Отже, це легко обчислити

\[\nabla u = (\dfrac{y^2 - x^2}{r^4}, \dfrac{-2xy}{r^4}) \text{ and } \nabla v = (\dfrac{2xy}{r^4}, \dfrac{y^2 - x^2}{r^4}).\]

Знову ж таки, це банально перевірити$\nabla u \cdot \nabla v = 0$, так що вони ортогональні.

Приклад$\PageIndex{3}$ Degenerate points: $f'(z) = 0$.

Розглянемо

\[f(z) = z^2\]

З попереднього прикладу ми маємо

\[u(x, y) = x^2 - y^2, \ \ \ v(x, y) = 2xy, \ \ \ \nabla u = (2x, -2y), \ \ \ \nabla v = (2y, 2x).\]

В$z = 0$, градієнти обидва 0, тому теорема про ортогональність не застосовується.

Давайте подивимося на криві рівня через початок. Крива рівня (насправді «набір рівнів») для

\[u = x^2 - y^2 = 0\]

це пара рядків$y = \pm x$. На початку це не плавна крива.

Подивіться на цифри$z^2$ вище. Здається, що далеко від початку криві рівня$u$ перетинають лінії, де$v = 0$ під прямим кутом. Те ж саме стосується кривих рівня$v$ та ліній, де$u = 0$. Ви можете побачити дегенерацію, що формується на початку: коли криві рівня спрямовуються до 0, вони стають більш точними і більш прямими кутами. Таким чином,$u = 0$ крива рівня більш правильно розглядається як чотири прямі кути. Крива рівня$u = 0$, не знаючи, який відрізок$v = 0$ перетинається ортогонально, приймає середнє значення і приходить в початок в 45$^{\circ}$.

Лемма\(\PageIndex{1}\)

Теорема\(\PageIndex{1}\)

Приклад\(\PageIndex{1}\)

Приклад\(\PageIndex{2}\)

Приклад\(\PageIndex{3}\) Degenerate points: \(f'(z) = 0\).