2.4: Точка на нескінченності
- Page ID
- 62584
За визначенням розширена комплексна площина\(= C \cup \{\infty\}\). Тобто у нас є одна точка на нескінченності, про яку слід думати в обмежуючому сенсі, описаному наступним чином.
Послідовність точок\(\{z_n\}\) переходить до нескінченності, якщо\(|z_n|\) йде до нескінченності. Ця «точка на нескінченності» наближається в будь-якому напрямку, в якому ми йдемо. Всі послідовності, показані на малюнку\(\PageIndex{1}\), зростають, тому всі вони йдуть до однієї (тієї ж) «точки на нескінченності».
Якщо ми намалюємо велике коло навколо 0 в площині, то область за межами цього кола називаємо околицем нескінченності (рис.\(\PageIndex{2}\)).
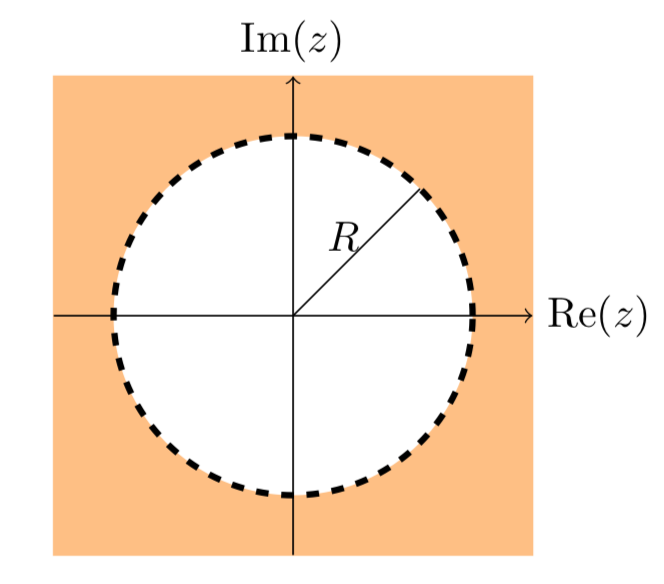
Межі за участю нескінчен
Ключовою ідеєю є\(1/\infty = 0\). Під цим ми маємо на увазі
\[\lim_{z \to \infty} \dfrac{1}{z} = 0\]
Потім ми маємо такі факти:
- \(\lim_{z \to z_0} f(z) = \infty \Leftrightarrow \lim_{z \to z_0} 1/f(z) = 0\)
- \(\lim_{z \to \infty} = w_0 \Leftrightarrow \lim_{z \to 0} f(1/z) = w_0\)
- \(\lim_{z \to \infty} = \infty \Leftrightarrow \lim_{z \to 0} \dfrac{1}{f(1/z)} = 0\)
\(\lim_{z \to \infty} e^z\)не визначено, оскільки воно має різні значення, якщо ми йдемо до нескінченності в різних напрямках, наприклад, у нас є\(e^z = e^x e^{iy}\) і
\(\lim_{x \to -\infty} e^x e^{iy} = 0\)
\(\lim_{x \to +\infty} e^x e^{iy} = \infty\)
\(\lim_{y \to +\infty} e^x e^{iy}\)не визначено, оскільки\(x\) є постійним, тому\(e^x e^{iy}\) петлі по колу нескінченно довго.
Показати\(\lim_{z \to \infty} z^n = \infty\) (для\(n\) натурального цілого числа).
Рішення
Нам потрібно показати, що\(|z^n|\) стає великим, як\(|z|\) стає великим. Пишіть\(z = Re^{i \theta}\), потім
\[|z^n| = |R^n e^{in \theta}| = R^n = |z|^n \nonumber\]
Стереографічна проекція зі сфери Рімана
Одним із способів візуалізації точки\(\infty\) є використання (одиниці) сфери Рімана та пов'язаної стереографічної проекції. \(\PageIndex{4}\)На малюнку зображена сфера, екватором якої є одиничне коло в комплексній площині.
Стереографічна проекція від сфери до площини здійснюється шляхом проведення січної лінії від північного полюса\(N\) через точку на сфері і бачачи, де вона перетинає площину. Це дає відповідність 1-1 між точкою на сфері\(P\) і точкою в комплексній площині\(z\). Легко побачити показати, що формула стереографічної проекції є
\[P = (a, b, c) \mapsto z = \dfrac{a}{1 - c} + i \dfrac{b}{1 - c}.\]
Точка\(N = (0, 0, 1)\) особлива, січні лінії від\(N\) наскрізного\(P\) стають дотичними лініями до сфери, на\(N\) якій ніколи не перетинаються площину. \(N\)Вважаємо точку на нескінченності.
На малюнку вище область поза великим колом через точку\(z\) є сусідством нескінченності. Він відповідає маленькій круглої ковпачку навколо\(N\) на сфері. Тобто маленька шапка навколо\(N\) - це сусідство точки на нескінченності на сфері!
\(\PageIndex{4}\)На малюнку показаний ще один поширений варіант стереографічної проекції. На цьому малюнку сфера сидить своїм південним полюсом біля початку. Ми все ще проектуємо, використовуючи січні лінії з північного полюса.
