6.4: Розриви похідних

Теорема$\PageIndex{1}$: Intermediate Value Theorem for Derivatives

Припустимо,$f$ диференціюється на відкритому інтервалі$I, a, b \in I,$$\lambda \in \mathbb{R}$ і$a<b .$ Якщо і$f^{\prime}(a)<\lambda<f^{\prime}(b)$ або або$f^{\prime}(a)>\lambda>f^{\prime}(b),$ то існує$c \in(a, b)$ таке, що$f^{\prime}(c)=\lambda$.

Доказ

Припустимо$f^{\prime}(a)<\lambda<f^{\prime}(b)$ і визначте$g: I \rightarrow \mathbb{R}$ по$g(x)=f(x)-\lambda x$. Потім$g$ диференціюється$I,$ і так безперервно на$[a, b] .$$c$ Дозволяти бути точкою,$[a, b]$ в якій$g$ досягає свого мінімального значення. Зараз

$$g^{\prime}(a)=f^{\prime}(a)-\lambda<0,$$

так існує$a<t<b$ таке, що

$$g(t)-g(a)<0.$$

Таким чином,$c \neq a .$ Аналогічно,

$$g^{\prime}(b)=f^{\prime}(b)-\lambda>0,$$

так існує$a<s<b$ таке, що

$$g(s)-g(b)<0.$$

Таким чином,$c \neq b .$ звідси$c \in(a, b),$ і так$g^{\prime}(c)=0 .$ Так$0=f^{\prime}(c)-\lambda,$ і так$f^{\prime}(c)=\lambda .$$\quad$ Q.E.D.

Вправа$\PageIndex{1}$

Визначте$g:(-1,1) \rightarrow \mathbb{R}$ по

$$g(x)=\left\{\begin{array}{cc}{-1,} & {\text { if }-1<x<0,} \\ {1,} & {\text { if } 0 \leq x<1.}\end{array}\right.$$

Чи існує$f:(-1,1) \rightarrow \mathbb{R}$ така функція, що$f^{\prime}(x)=g(x)$ для всіх$x \in(-1,1) ?$

Вправа$\PageIndex{2}$

Припустимо$f$, диференційований на відкритому інтервалі$I .$ Показати, що$f^{\prime}$ не може мати жодних простих розривів в$I$.

Приклад$\PageIndex{1}$

Визначити$\varphi:[0,1] \rightarrow \mathbb{R}$$\rho: \mathbb{R} \rightarrow \mathbb{R}$ по$\varphi(x)=x(2 x-1)(x-1) .$ Визначити$\rho(x)=6 x^{2}-6 x+1 .$ потім

$$\varphi(x)=2 x^{3}-3 x^{2}+x,$$

так$\varphi^{\prime}(x)=\rho(x)$ для всіх$x \in(0,1) .$ Далі визначте$s: \mathbb{R} \rightarrow \mathbb{R}$ по$s(x)=\varphi(x-\lfloor x\rfloor)$. Див. Рисунок$\PageIndex{1}$ для графіків$\varphi$ і$s .$ Тоді для будь-якого$n \in \mathbb{Z}$ і$n<x<n+1$,

$$s^{\prime}(x)=\rho(x-n)=\rho(x-\lfloor x\rfloor).$$

Більш того, якщо$x$ є цілим числом,

$$\begin{aligned} \lim _{h \rightarrow 0^{+}} \frac{s(x+h)-s(x)}{h} &=\lim _{h \rightarrow 0^{+}} \frac{\varphi(h)}{h} \\ &=\lim _{h \rightarrow 0^{+}} \frac{h(2 h-1)(h-1)}{h} \\ &=\lim _{h \rightarrow 0^{+}}(2 h-1)(h-1) \\ &=1 \end{aligned}$$

і

$$\begin{aligned} \lim _{h \rightarrow 0^{-}} \frac{s(x+h)-s(x)}{h} &=\lim _{h \rightarrow 0^{-}} \frac{\varphi(h+1)}{h} \\ &=\lim _{h \rightarrow 0^{-}} \frac{(h+1)(2 h+1) h}{h} \\ &=\lim _{h \rightarrow 0^{-}}(h+1)(2 h+1) \\ &=1. \end{aligned}$$

Малюнок$\PageIndex{1}$: Графіки$y=\varphi(x)$ і$y=s(x)$

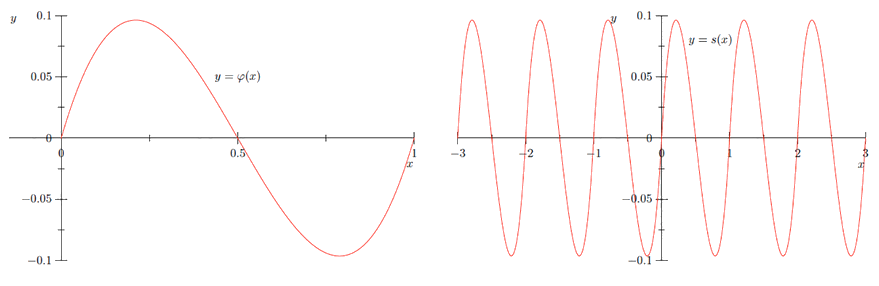
Таким чином,$s^{\prime}(x)=1=\rho(x-\lfloor x\rfloor)$$x$ коли ціле число, і так$s^{\prime}(x)=\rho(x-\lfloor x\rfloor)$ для всіх$x \in \mathbb{R} .$

Тепер,$\rho(x)=0$ якщо і тільки якщо$x=\frac{3-\sqrt{3}}{6}$ або$x=\frac{3+\sqrt{3}}{6} .$ з тих пір$\varphi(0)=0$,$\varphi\left(\frac{3-\sqrt{3}}{6}\right)=\frac{1}{6 \sqrt{3}}, \varphi\left(\frac{3+\sqrt{3}}{6}\right)=-\frac{1}{6 \sqrt{3}},$ і$\varphi(1)=0,$ ми бачимо, що$\varphi$ досягає

максимальне значення$\frac{1}{6 \sqrt{3}}$ і мінімальне значення$-\frac{1}{6 \sqrt{3}} .$ Звідси для будь-якого$n \in \mathbb{Z}$,

$$s((n, n+1))=\left[-\frac{1}{6 \sqrt{3}}, \frac{1}{6 \sqrt{3}}\right].$$

Крім того,$\rho^{\prime}(x)=12 x-6,$ так$\rho^{\prime}(x)=0$ якщо і тільки якщо$x=\frac{1}{2} .$ з тих пір$\rho(0)=1$,$\rho\left(\frac{1}{2}\right)=-\frac{1}{2},$ і$\rho(1)=1,$ ми бачимо, що$\rho$ досягає максимального значення 1 і v,

$$s^{\prime}((n, n+1))=\left[-\frac{1}{2}, 1\right].$$

З попереднього, таким же чином, як результат у прикладі, випливає$5.1 .7,$, що ні функція,$\sigma(x)=s\left(\frac{1}{x}\right)$ ні функція не мають обмеження, як$x$ наближається$g(x)=s^{\prime}\left(\frac{1}{x}\right)$$0 .$

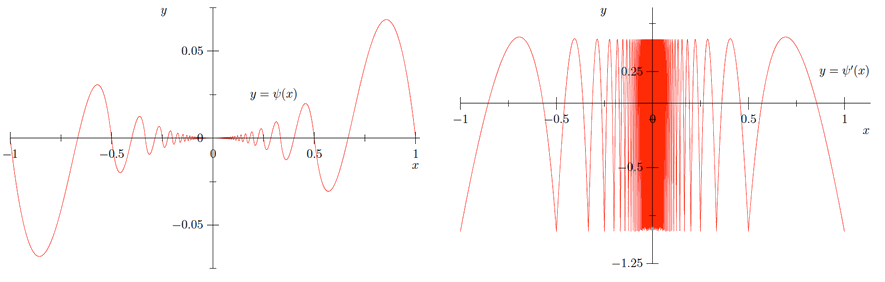
Нарешті,$\psi: \mathbb{R} \rightarrow \mathbb{R}$ визначте

$$\psi(x)=\left\{\begin{array}{ll}{x^{2} s\left(\frac{1}{x}\right),} & {\text { if } x \neq 0,} \\ {0,} & {\text { if } x=0.}\end{array}\right.$$

Бо у$x \neq 0,$ нас є

$$\psi^{\prime}(x)=x^{2} s^{\prime}\left(\frac{1}{x}\right)\left(-\frac{1}{x^{2}}\right)+2 x s\left(\frac{1}{x}\right)=-s^{\prime}\left(\frac{1}{x}\right)+2 x s\left(\frac{1}{x}\right).$$

У$0,$ нас є

$$\begin{aligned} \psi^{\prime}(0) &=\lim _{h \rightarrow 0} \frac{\psi(0+h)-\psi(0)}{h} \\ &=\lim _{h \rightarrow 0} \frac{h^{2} s\left(\frac{1}{h}\right)}{h} \\ &=\lim _{h \rightarrow 0} h s\left(\frac{1}{h}\right) \\ &=0, \end{aligned}$$

де кінцева межа випливає з теореми стискання і того, що$s$ обмежена. Отже, ми бачимо, що$\psi$ є безперервним$\mathbb{R}$ і диференційованим,$\mathbb{R},$ але не$\psi^{\prime}$ є безперервним, оскільки$\psi^{\prime}(x)$ не має межі, як$x$ підходи$0 .$ Див. Рисунок$\PageIndex{1}$ для графіків$\psi$ і$\psi^{\prime} .$

Малюнок$\PageIndex{2}$: Графіки$y=\psi(x)$ і$y=\psi^{\prime}(x)$.

Вправа$\PageIndex{3}$

$s$Дозволяти бути як зазначено вище і визначити$g: \mathbb{R} \rightarrow \mathbb{R}$

$$g(x)=\left\{\begin{array}{ll}{x^{4} s\left(\frac{1}{x}\right),} & {\text { if } x \neq 0} \\ {0,} & {\text { if } x=0.}\end{array}\right.$$

Показати, що$g$ є$\mathbb{R}$ диференційованим і$g^{\prime}$ що безперервно на$\mathbb{R}$.