11.6E: Вправи

Last updated

Oct 27, 2022
Save as PDF
- 11.6: Розв'язування систем нелінійних рівнянь
- Глава 11 Огляд вправ

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Практика робить досконалим

Вправа $\PageIndex{17}$ Solve a System of Nonlinear Equations Using Graphing

У наступних вправах розв'яжіть систему рівнянь за допомогою графіки.

$\left\{\begin{array}{l}{y=2 x+2} \\ {y=-x^{2}+2}\end{array}\right.$
$\left\{\begin{array}{l}{y=6 x-4} \\ {y=2 x^{2}}\end{array}\right.$
$\left\{\begin{array}{l}{x+y=2} \\ {x=y^{2}}\end{array}\right.$
$\left\{\begin{array}{l}{x-y=-2} \\ {x=y^{2}}\end{array}\right.$
$\left\{\begin{array}{l}{y=\frac{3}{2} x+3} \\ {y=-x^{2}+2}\end{array}\right.$
$\left\{\begin{array}{l}{y=x-1} \\ {y=x^{2}+1}\end{array}\right.$
$\left\{\begin{array}{l}{x=-2} \\ {x^{2}+y^{2}=4}\end{array}\right.$
$\left\{\begin{array}{l}{y=-4} \\ {x^{2}+y^{2}=16}\end{array}\right.$
$\left\{\begin{array}{l}{x=2} \\ {(x+2)^{2}+(y+3)^{2}=16}\end{array}\right.$
$\left\{\begin{array}{l}{y=-1} \\ {(x-2)^{2}+(y-4)^{2}=25}\end{array}\right.$
$\left\{\begin{array}{l}{y=-2 x+4} \\ {y=\sqrt{x}+1}\end{array}\right.$
$\left\{\begin{array}{l}{y=-\frac{1}{2} x+2} \\ {y=\sqrt{x}-2}\end{array}\right.$

Відповідь

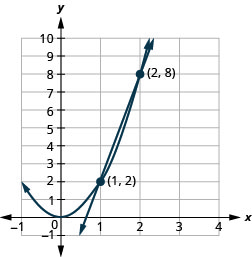
Цей графік показує рівняння системи, y дорівнює 6 х мінус 4, що є прямою, а y дорівнює 2 х квадрат, що є параболою, на координатній площині x y. Вершина параболи дорівнює (0, 0), а парабола відкривається вгору. Лінія має ухил 6. Лінія і парабола перетинаються в точках (1, 2) і (2, 8), які позначені. Рішення є (1, 2) і (2, 8). — Малюнок 11.5.61

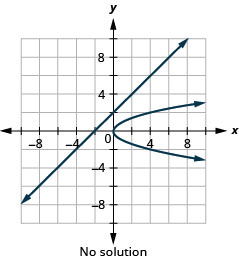
Цей графік показує рівняння системи, x мінус y дорівнює від'ємному 2, який є прямою, а x дорівнює y квадрату, який є параболою, що відкривається праворуч, на координатній площині x y. Вершина параболи дорівнює (0, 0) і вона проходить через точки (1, 1) і (1, негативний 1). Лінія має нахил 1 і y-перехоплення на 2. Лінія і парабола не перетинаються, тому система не має рішення. — Малюнок 11.5.62

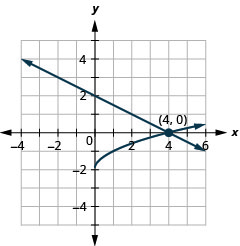
Цей графік показує рівняння системи, y дорівнює x мінус 1, яка є лінією, а y дорівнює x у квадраті плюс 1, що є параболою, що відкривається вгору, на координатній площині x y. Вершина параболи дорівнює (0, 1) і вона проходить через точки (негативні 1, 2) і (1, 2). Лінія має нахил 1 і y-перехоплення при негативному 1. Лінія і парабола не перетинаються, тому система не має рішення. — Малюнок 11.5.63

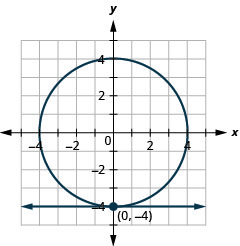
Цей графік показує рівняння системи, x дорівнює від'ємному 2, який є прямою, а x у квадраті плюс y в квадраті дорівнює 16, що є колом, на координатній площині x y. Лінія горизонтальна. Центр кола дорівнює (0, 0), а радіус кола - 4. Лінія і коло перетинаються на (від'ємний 2, 0), тому рішення системи є (негативним 2, 0). — Малюнок 11.5.64

10.

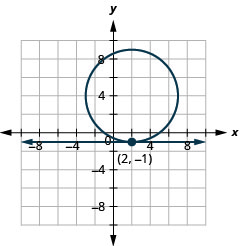
Цей графік показує рівняння системи, x дорівнює 2, яка є лінією, а кількість x мінус 2 кінцева кількість у квадраті плюс кількість y мінус 4 кінцева кількість у квадраті дорівнює 25, що є колом, на координатній площині x y. Лінія горизонтальна. Центр кола - (2, 4), а радіус кола - 5. Лінія і коло перетинаються на (2, від'ємний 1), тому рішення системи є (2, негативним 1). — Малюнок 11.5.65

12.

Цей графік показує рівняння системи, y дорівнює від'ємній половині x плюс 2, яка є прямою, а y дорівнює квадратному кореню x мінус 2, на координатній площині x y. Крива для y дорівнює квадратному кореню x мінус 2 Крива для y дорівнює квадратному кореню x плюс 1, де x більше або дорівнює 0, а y більше або дорівнює від'ємному 2. Лінія та квадратна коренева крива перетинаються на (4, 0), тому рішення є (4, 0). — Малюнок 11.5.66

Вправа $\PageIndex{18}$ Solve a System of Nonlinear Equations Using Substitution

У наступних вправах вирішуйте систему рівнянь за допомогою підстановки.

$\left\{\begin{array}{l}{x^{2}+4 y^{2}=4} \\ {y=\frac{1}{2} x-1}\end{array}\right.$
$\left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=3 x+3}\end{array}\right.$
$\left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=x+3}\end{array}\right.$
$\left\{\begin{array}{l}{9 x^{2}+4 y^{2}=36} \\ {x=2}\end{array}\right.$
$\left\{\begin{array}{l}{4 x^{2}+y^{2}=4} \\ {y=4}\end{array}\right.$
$\left\{\begin{array}{l}{x^{2}+y^{2}=169} \\ {x=12}\end{array}\right.$
$\left\{\begin{array}{l}{3 x^{2}-y=0} \\ {y=2 x-1}\end{array}\right.$
$\left\{\begin{array}{l}{2 y^{2}-x=0} \\ {y=x+1}\end{array}\right.$
$\left\{\begin{array}{l}{y=x^{2}+3} \\ {y=x+3}\end{array}\right.$
$\left\{\begin{array}{l}{y=x^{2}-4} \\ {y=x-4}\end{array}\right.$
$\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {x-y=1}\end{array}\right.$
$\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {2 x+y=10}\end{array}\right.$

Відповідь

2. $(-1,0),(0,3)$

4. $(2,0)$

6. $(12,-5),(12,5)$

8. Немає рішення

10. $(0,-4),(1,-3)$

12. $(3,4),(5,0)$

Вправа $\PageIndex{19}$ Solve a System of Nonlinear Equations Using Elimination

У наступних вправах вирішуйте систему рівнянь за допомогою елімінації.

$\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-2 y=8}\end{array}\right.$
$\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-y=4}\end{array}\right.$
$\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}+2 y=1}\end{array}\right.$
$\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}-y=2}\end{array}\right.$
$\left\{\begin{array}{l}{x^{2}+y^{2}=9} \\ {x^{2}-y=3}\end{array}\right.$
$\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {y^{2}-x=2}\end{array}\right.$
$\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {2 x^{2}-3 y^{2}=5}\end{array}\right.$
$\left\{\begin{array}{l}{x^{2}+y^{2}=20} \\ {x^{2}-y^{2}=-12}\end{array}\right.$
$\left\{\begin{array}{l}{x^{2}+y^{2}=13} \\ {x^{2}-y^{2}=5}\end{array}\right.$
$\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-y^{2}=16}\end{array}\right.$
$\left\{\begin{array}{l}{4 x^{2}+9 y^{2}=36} \\ {2 x^{2}-9 y^{2}=18}\end{array}\right.$
$\left\{\begin{array}{l}{x^{2}-y^{2}=3} \\ {2 x^{2}+y^{2}=6}\end{array}\right.$
$\left\{\begin{array}{l}{4 x^{2}-y^{2}=4} \\ {4 x^{2}+y^{2}=4}\end{array}\right.$
$\left\{\begin{array}{l}{x^{2}-y^{2}=-5} \\ {3 x^{2}+2 y^{2}=30}\end{array}\right.$
$\left\{\begin{array}{l}{x^{2}-y^{2}=1} \\ {x^{2}-2 y=4}\end{array}\right.$
$\left\{\begin{array}{l}{2 x^{2}+y^{2}=11} \\ {x^{2}+3 y^{2}=28}\end{array}\right.$

Відповідь

2. $(0,-4),(-\sqrt{7}, 3),(\sqrt{7}, 3)$

4. $(0,-2),(-\sqrt{3}, 1),(\sqrt{3}, 1)$

6. $(-2,0),(1,-\sqrt{3}),(1, \sqrt{3})$

8. $(-2,-4),(-2,4),(2,-4),(2,4)$

10. $(-4,0),(4,0)$

12. $(-\sqrt{3}, 0),(\sqrt{3}, 0)$

14. $(-2,-3),(-2,3),(2,-3),(2,3)$

16. $(-1,-3),(-1,3),(1,-3),(1,3)$

Вправа $\PageIndex{20}$ Use a System of Nonlinear Equations to Solve Applications

У наступних вправах вирішуйте задачу за допомогою системи рівнянь.

Сума двох чисел є, $−6$ а добуток дорівнює $8$ . Знайдіть цифри.
Сума двох чисел є, $11$ а добуток дорівнює $−42$ . Знайдіть цифри.
Сума квадратів двох чисел дорівнює $65$ . Різниця числа є $3$ . Знайдіть цифри.
Сума квадратів двох чисел дорівнює $113$ . Різниця числа є $1$ . Знайдіть цифри.
Різниця квадратів двох чисел дорівнює $15$ . Різниця в два рази більше квадрата першого числа і квадрата другого числа дорівнює $30$ . Знайдіть цифри.
Різниця квадратів двох чисел дорівнює $20$ . Різниця квадрата першого числа і подвійного квадрата другого числа дорівнює $4$ . Знайдіть цифри.
Периметр прямокутника дорівнює $32$ дюймам, а його площа - $63$ квадратні дюйми. Знайдіть довжину і ширину прямокутника.
Периметр прямокутника - $52$ см, а його площа - $165$ $\mathrm{cm}^{2}$ . Знайдіть довжину і ширину прямокутника.
Діон придбав нову мікрохвильовку. Діагональ дверей вимірює $17$ дюйми. Двері також мають площу $120$ квадратних дюймів. Яка довжина і ширина дверцята мікрохвильовки?
Жюль придбав мікрохвильовку для своєї кухні. Діагональ передньої частини мікрохвильовки вимірює $26$ дюйми. Передня частина також має площу $240$ квадратних дюймів. Яка довжина і ширина мікрохвильовки?
Роман знайшов у продажу широкоекранний телевізор, але не впевнений, чи підійде він до його розважального центру. Телевізор є $60$ ». Розмір телевізора вимірюється по діагоналі екрану, а широкоформатний має довжину, яка більше ширини. Екран також має площу $1728$ квадратних дюймів. Його розважальний центр має вставку для телевізора довжиною в $50$ дюйми і шириною в $40$ дюйми. Яка довжина і ширина екрану телевізора і чи підійде він до розважального центру Романа?
Доннетт знайшов широкоекранний телевізор на продажу гаража, але не впевнений, чи підійде він до її розважального центру. Телевізор є $50$ ». Розмір телевізора вимірюється по діагоналі екрану, а широкоформатний має довжину, яка більше ширини. Екран також має площу $1200$ квадратних дюймів. Її розважальний центр має вставку для телевізора довжиною в $38$ дюйми і шириною в $27$ дюйми. Яка довжина і ширина екрану телевізора і чи підійде він розважальному центру Доннетт?

Відповідь

2. $-3$ і $14$

4. $-7$ і $-8$ або $8$ і $7$

6. $-6$ $-6$ і $-4$ або $4$ і/або $6$ $-4$ і/або $6$ і $4$

8. Якщо довжина - $11$ см, ширина - $15$ см. Якщо довжина - $15$ см, ширина - $11$ см.

10. Якщо довжина дорівнює $10$ дюймам, ширина дорівнює $24$ дюймам. Якщо довжина дорівнює $24$ дюймам, ширина дорівнює $10$ дюймам.

12. Довжина - $40$ дюйми, а ширина - $30$ дюйми. Телевізор не підійде розважальному центру Доннет.

Вправа $\PageIndex{21}$ Writing Exercises

Своїми словами поясніть переваги та недоліки рішення системи рівнянь графіком.
Поясніть своїми словами, як вирішити систему рівнянь за допомогою підстановки.
Поясніть своїми словами, як вирішити систему рівнянь за допомогою елімінації.
Коло і парабола можуть перетинатися способами, які призведуть до $0, 1, 2, 3,$ або $4$ рішень. Намалюйте ескіз кожної з можливостей.

Відповідь

2. Відповіді можуть відрізнятися

4. Відповіді можуть відрізнятися

Самостійна перевірка

а Після виконання вправ використовуйте цей контрольний список, щоб оцінити своє володіння цілями цього розділу.

Ця таблиця складається з чотирьох стовпців і п'яти рядків. Перший рядок є заголовком, і він позначає кожен стовпець, â € œi canâ€â€, â€œвпевнено, â€ â€ â€œЗ деякою допомогою, â€ і â€œno-i donâ€™ t отримати його! â € У рядку 2, я можу вирішити систему нелінійних рівнянь за допомогою графіки. У рядку 3 I можна вирішити систему нелінійних рівнянь за допомогою підстановки. У рядку 4 I can було вирішено систему нелінійних рівнянь за допомогою елімінації. У рядку 5 я можу використовувати систему нелінійних рівнянь для розв'язання додатків. — Малюнок 11.5.67

б Подивившись контрольний список, ви вважаєте, що добре підготовлені до наступного розділу? Чому чи чому ні?

Практика робить досконалим

Вправа11.6E.17\PageIndex{17} Solve a System of Nonlinear Equations Using Graphing

Вправа11.6E.18\PageIndex{18} Solve a System of Nonlinear Equations Using Substitution

Вправа11.6E.19\PageIndex{19} Solve a System of Nonlinear Equations Using Elimination

Вправа11.6E.20\PageIndex{20} Use a System of Nonlinear Equations to Solve Applications

Вправа11.6E.21\PageIndex{21} Writing Exercises

Самостійна перевірка

Вправа $\PageIndex{17}$ Solve a System of Nonlinear Equations Using Graphing

Вправа $\PageIndex{18}$ Solve a System of Nonlinear Equations Using Substitution

Вправа $\PageIndex{19}$ Solve a System of Nonlinear Equations Using Elimination

Вправа $\PageIndex{20}$ Use a System of Nonlinear Equations to Solve Applications

Вправа $\PageIndex{21}$ Writing Exercises