11.6: Розв'язування систем нелінійних рівнянь

Цілі навчання

До кінця цього розділу ви зможете:

• Розв'яжіть систему нелінійних рівнянь за допомогою графіків
• Розв'язувати систему нелінійних рівнянь за допомогою підстановки
• Розв'язувати систему нелінійних рівнянь за допомогою елімінації
• Використовувати систему нелінійних рівнянь для розв'язання додатків

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

1. Вирішіть систему за допомогою графіків:$\left\{\begin{array}{l}{x-3 y=-3} \\ {x+y=5}\end{array}\right.$.
   Якщо ви пропустили цю проблему, перегляньте приклад 4.2.
2. Вирішити систему шляхом підміни:$\left\{\begin{array}{l}{x-4 y=-4} \\ {-3 x+4 y=0}\end{array}\right.$
   Якщо ви пропустили цю проблему, перегляньте приклад 4.7.
3. Вирішити систему шляхом усунення:$\left\{\begin{array}{l}{3 x-4 y=-9} \\ {5 x+3 y=14}\end{array}\right.$
   Якщо ви пропустили цю проблему, перегляньте приклад 4.9.

Розв'язування системи нелінійних рівнянь за допомогою графіків

Ми навчилися розв'язувати системи лінійних рівнянь з двома змінними шляхом побудови графіків, заміщення та усунення. Ми будемо використовувати ці самі методи, коли ми розглянемо нелінійні системи рівнянь з двома рівняннями і двома змінними. Система нелінійних рівнянь - це система, де принаймні одне з рівнянь не є лінійним.

Наприклад, кожна з наступних систем являє собою систему нелінійних рівнянь.

$\left\{\begin{array}{l}{x^{2}+y^{2}=9} \\ {x^{2}-y=9}\end{array}\right. \left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=3 x-3}\end{array}\right. \left\{\begin{array}{l}{x+y=4} \\ {y=x^{2}+2}\end{array}\right.$

Визначення$\PageIndex{1}$

Система нелінійних рівнянь - це система, де принаймні одне з рівнянь не є лінійним.

Подібно до систем лінійних рівнянь, розв'язок нелінійної системи - це впорядкована пара, яка робить обидва рівняння істинними. У нелінійній системі може бути більше одного рішення. Ми побачимо це, коли розв'яжемо систему нелінійних рівнянь за допомогою графіків.

Коли ми розв'язували системи лінійних рівнянь, рішенням системи була точка перетину двох прямих. При системах нелінійних рівнянь графіки можуть бути колами, параболами або гіперболами і може бути кілька точок перетину, і так кілька рішень. Після того, як ви ідентифікуєте графіки, візуалізуйте різні способи перетину графіків і скільки рішень може бути.

Для розв'язання систем нелінійних рівнянь шляхом побудови графіків використовуються в основному ті ж кроки, що і для систем лінійних рівнянь, дещо модифікованих для нелінійних рівнянь. Кроки наведені нижче для довідки.

Розв'яжіть систему нелінійних рівнянь за допомогою графіків.

1. Визначте графік кожного рівняння. Намалюйте можливі варіанти перетину.
2. Графік першого рівняння.
3. Графік другого рівняння на тій же прямокутній системі координат.
4. Визначте, чи перетинаються графіки.
5. Визначте точки перетину.
6. Переконайтеся, що кожна впорядкована пара є розв'язком обох вихідних рівнянь.

Приклад$\PageIndex{1}$

Вирішіть систему за допомогою графіків:$\left\{\begin{array}{l}{x-y=-2} \\ {y=x^{2}}\end{array}\right.$

Рішення:

Таблиця 11.5.1

Визначте кожен графік.	$\left\{\begin{array}{ll}{x-y=-2} & {\text { line }} \\ {y=x^{2}} & {\text { parabola }}\end{array}\right.$
Намалюйте можливі варіанти перетину параболи і лінії.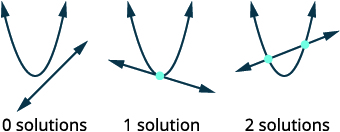
Графік лінії,$x-y=-2$. Ухил-перехоплення форма$y=x+2$. Графік параболи,$y=x^{2}$.
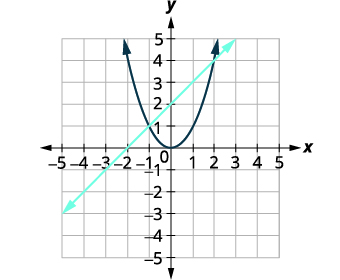Визначте точки перетину.	Точки перетину здаються$(2,3)$ і$(-1,1)$.
Перевірте, щоб переконатися, що кожне рішення робить обидва рівняння істинними. $(2,4)$ $\begin{array} {r l } {x-y=-2}\quad\quad {y=x^{2}} \\ {2-4\stackrel{?}{=}-2}\quad\quad {4\stackrel{?}{=}2^{2}} \\ {-2 = -2}\quad\quad\:{4 = 4} \end{array}$ $(-1,1)$ $\begin{array} {l l } {x-y=-2}\quad\quad {y=x^{2}} \\ {-1-1\stackrel{?}{=}-2}\:\quad {1\stackrel{?}{=}(-1)^{2}} \\ {-2 = -2}\quad\quad\quad{1 = 1} \end{array}$
	Рішення є$(2,4)$ і$(-1,1)$.

Вправа$\PageIndex{1}$

Вирішіть систему за допомогою графіків:$\left\{\begin{array}{l}{x+y=4} \\ {y=x^{2}+2}\end{array}\right.$.

Відповідь

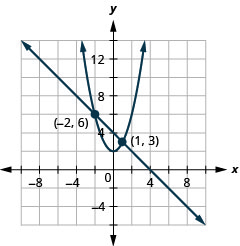
Малюнок 11.5.3

Вправа$\PageIndex{2}$

Вирішіть систему за допомогою графіків:$\left\{\begin{array}{l}{x-y=-1} \\ {y=-x^{2}+3}\end{array}\right.$

Відповідь

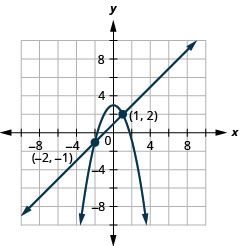
Малюнок 11.5.4

Щоб ідентифікувати графік кожного рівняння, майте на увазі характеристики$x^{2}$ і$y^{2}$ членів кожного конічного конуса.

Приклад$\PageIndex{2}$

Вирішіть систему за допомогою графіків:$\left\{\begin{array}{l}{y=-1} \\ {(x-2)^{2}+(y+3)^{2}=4}\end{array}\right.$.

Рішення:

Таблиця 11.5.2

Визначте кожен графік.	$\left\{\begin{array}{ll}{y=-1} & {\text { line }} \\ {(x-2)^{2}+(y+3)^{2}=4} & {\text { circle }}\end{array}\right.$
Намалюйте можливі варіанти перетину кола і лінії.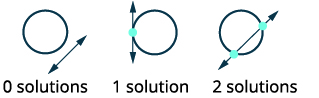
Графік кола,$(x-2)^{2}+(y+3)^{2}=4$ Центр:$(2,-3)$ радіус:$2$ Графік лінії,$y=-1$. Вона являє собою горизонтальну лінію.
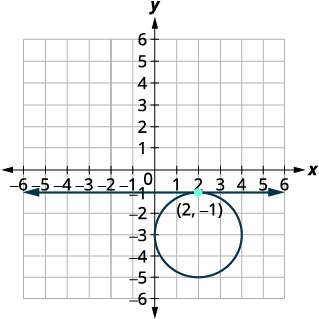Визначте точки перетину.	Точка перетину, здається, є$(2,-1)$.
Переконайтеся, що рішення робить обидва рівняння істинними. $(2,-1)$ $\begin{array} {r r} {(x-2)^{2}+(y+3)^{2}=4} \quad\quad {y=-1} \\ {(2-2)^{2}+(-1+3)^{2}\stackrel{?}{=}4}\quad{-1=-1} \\ {(0)^{2}+(2)^{2}\stackrel{?}{=}4}\quad\quad\quad\quad\quad \\ {4=4}\quad\quad\quad\quad\quad \end{array}$
	Рішення є$(2,-1)$

Вправа$\PageIndex{3}$

Вирішіть систему за допомогою графіків:$\left\{\begin{array}{l}{x=-6} \\ {(x+3)^{2}+(y-1)^{2}=9}\end{array}\right.$

Відповідь

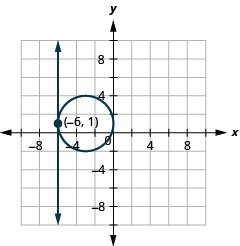
Малюнок 11.5.7

Вправа$\PageIndex{4}$

Вирішіть систему за допомогою графіків:$\left\{\begin{array}{l}{y=4} \\ {(x-2)^{2}+(y+3)^{2}=4}\end{array}\right.$

Відповідь

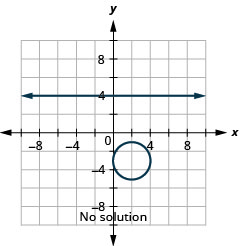
Малюнок 11.5.8

Розв'язування системи нелінійних рівнянь за допомогою заміщення

Метод графіки добре працює, коли точки перетину є цілими числами і так легко зчитується з графіка. Але частіше важко зчитувати координати точок перетину. Метод заміщення - це алгебраїчний метод, який буде добре працювати в багатьох ситуаціях. Він працює особливо добре, коли легко вирішити одне з рівнянь для однієї зі змінних.

Метод заміщення дуже схожий на метод заміщення, який ми використовували для систем лінійних рівнянь. Кроки наведені нижче для довідки.

Розв'язування системи нелінійних рівнянь заміщенням

1. Визначте графік кожного рівняння. Намалюйте можливі варіанти перетину.
2. Розв'яжіть одне з рівнянь для будь-якої змінної.
3. Підставте вираз з кроку 2 в інше рівняння.
4. Вирішити отримане рівняння.
5. Замініть кожне рішення на кроці 4 на одне з вихідних рівнянь, щоб знайти іншу змінну.
6. Запишіть кожне рішення як впорядковану пару.
7. Переконайтеся, що кожна впорядкована пара є розв'язком обох вихідних рівнянь.

Приклад$\PageIndex{3}$

Вирішити систему можна за допомогою підміни:$\left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=3 x-3}\end{array}\right.$

Рішення:

Таблиця 11.5.3

Визначте кожен графік.	$\left\{\begin{array}{ll}{9 x^{2}+y^{2}=9} & {\text { ellipse }} \\ {y=3 x-3} & {\text { line }}\end{array}\right.$
Намалюйте можливі варіанти перетину еліпса та лінії.
Рівняння$y=3x-3$ вирішується для$y$.
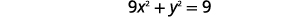$3x-3$Замініть$y$ в першому рівнянні.
Розв'яжіть рівняння для$x$.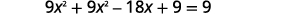
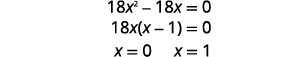$x=1$Підставити$x=0$ і$y=3x-3$ в знайти$y$ -.
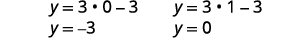	Впорядковані пари є$(0,-3), (1,0)$.
Перевірте обидві впорядковані пари в обох рівняннях. $(0,-3)$ $\begin{array} {r l}{9 x^{2}+y^{2}=9} &\quad { y=3 x-3} \\ {9\cdot0^{2}+(-3)^{2}\stackrel{?}{=}9}&\quad{-3\stackrel{?}{=}3\cdot0-3} \\ {0+9\stackrel{?}{=}9}&\quad{-3\stackrel{?}{=}0-3} \\ {9=9}&\quad{-3=-3} \end{array}$ $(1,0)$ $\begin{array} {r l}{9 x^{2}+y^{2}=9} &\quad { y=3 x-3} \\ {9\cdot 1^{2}+(0)^{2}\stackrel{?}{=}9}&\quad{0\stackrel{?}{=}3\cdot 1-3} \\ {9+0\stackrel{?}{=}9}&\quad{0\stackrel{?}{=}3-3} \\ {9=9}&\quad{0=0} \end{array}$
	Рішення є$(0,-3), (1,0)$.

Вправа$\PageIndex{5}$

Вирішити систему можна за допомогою підміни:$\left\{\begin{array}{l}{x^{2}+9 y^{2}=9} \\ {y=\frac{1}{3} x-3}\end{array}\right.$

Відповідь

Немає рішення

Вправа$\PageIndex{6}$

Вирішити систему можна за допомогою підміни:$\left\{\begin{array}{l}{4 x^{2}+y^{2}=4} \\ {y=x+2}\end{array}\right.$

Відповідь

$\left(-\frac{4}{5}, \frac{6}{5}\right),(0,2)$

Поки що кожна система нелінійних рівнянь мала принаймні одне рішення. Наступний приклад покаже інший варіант.

Приклад$\PageIndex{4}$

Вирішити систему можна за допомогою підміни:$\left\{\begin{array}{l}{x^{2}-y=0} \\ {y=x-2}\end{array}\right.$

Рішення:

Таблиця 11.5.4

Визначте кожен графік.	$\left\{\begin{array}{ll}{x^{2}-y=0} & {\text { parabola }} \\ {y=x-2} & {\text { line }}\end{array}\right.$
Намалюйте можливі варіанти перетину параболи і лінії.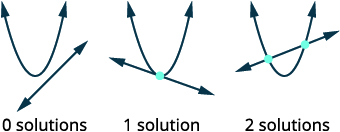
Рівняння$y=x-2$ вирішується для$y$.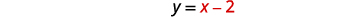
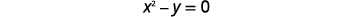$x-2$Замініть$y$ в першому рівнянні.
Розв'яжіть рівняння для$x$.
Це не легко фактор, тому ми можемо перевірити дискримінант.
$\begin{array}{c}{b^{2}-4 a c} \\ {(-1)^{2}-4 \cdot 1 \cdot 2} \\ {-7}\end{array}$	Дискримінант негативний, тому реального рішення не існує. Система не має рішення.

Вправа$\PageIndex{7}$

Вирішити систему можна за допомогою підміни:$\left\{\begin{array}{l}{x^{2}-y=0} \\ {y=2 x-3}\end{array}\right.$

Відповідь

Немає рішення

Вправа$\PageIndex{8}$

Вирішити систему можна за допомогою підміни:$\left\{\begin{array}{l}{y^{2}-x=0} \\ {y=3 x-2}\end{array}\right.$

Відповідь

$\left(\frac{4}{9},-\frac{2}{3}\right),(1,1)$

Розв'язування системи нелінійних рівнянь за допомогою елімінації

Коли ми вивчали системи лінійних рівнянь, ми використовували метод ліквідації для розв'язання системи. Ми також можемо використовувати елімінацію для розв'язання систем нелінійних рівнянь. Це добре працює, коли рівняння мають обидві змінні в квадраті. Використовуючи елімінацію, ми намагаємося зробити коефіцієнти однієї змінної протилежними, тому, коли ми додаємо рівняння разом, ця змінна усувається.

Метод елімінації дуже схожий на метод елімінації, який ми використовували для систем лінійних рівнянь. Кроки наведені для довідки.

Вирішити систему рівнянь шляхом ліквідації

1. Визначте графік кожного рівняння. Намалюйте можливі варіанти перетину.
2. Запишіть обидва рівняння в стандартній формі.
3. Складіть коефіцієнти однієї змінної протилежності.
   Вирішіть, яку змінну ви будете ліквідувати.
   Помножте одне або обидва рівняння так, щоб коефіцієнти цієї змінної були протилежними.
4. Додайте рівняння, отримані з кроку 3, щоб усунути одну змінну.
5. Вирішити для залишилася змінної.
6. Замініть кожне рішення з кроку 5 в одне з вихідних рівнянь. Потім вирішуйте для іншої змінної.
7. Запишіть кожне рішення як впорядковану пару.
8. Переконайтеся, що кожна впорядкована пара є розв'язком обох вихідних рівнянь.

Приклад$\PageIndex{5}$

Вирішити систему шляхом усунення:$\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}-y=4}\end{array}\right.$

Рішення:

Таблиця 11.5.5

Визначте кожен графік.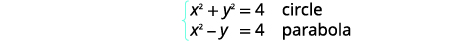
Намалюйте можливі варіанти перетину кола і параболи.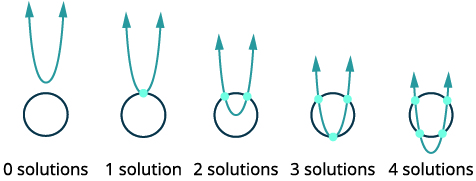
Обидва рівняння мають стандартну форму.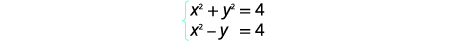
Щоб отримати протилежні коефіцієнти$x^{2}$, помножимо друге рівняння на$-1$.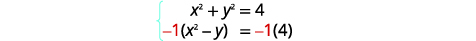
Спростити.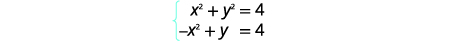
Додайте два рівняння для усунення$x^{2}$/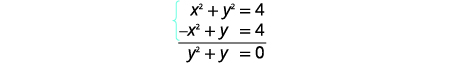
Вирішити для$y$.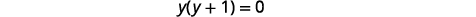
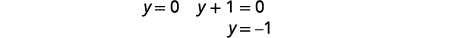$y=-1$Підставляємо$y=0$ і в одне з вихідних рівнянь. Тоді вирішуйте для$x$.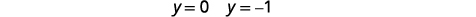
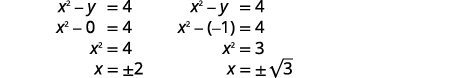Запишіть кожне рішення як впорядковану пару.	Впорядковані пари є$(-2,0)(2,0)$. $(\sqrt{3},-1)(-\sqrt{3},-1)$
Переконайтеся, що кожна впорядкована пара є розв'язком обох вихідних рівнянь.
Ми залишимо вам чеки для кожного з чотирьох рішень.	Рішення є$(-2,0),(2,0),(\sqrt{3},-1)$, і$(-\sqrt{3},-1)$.

Вправа$\PageIndex{9}$

Вирішити систему шляхом усунення:$\left\{\begin{array}{l}{x^{2}+y^{2}=9} \\ {x^{2}-y=9}\end{array}\right.$

Відповідь

$(-3,0),(3,0),(-2 \sqrt{2},-1),(2 \sqrt{2},-1)$

Вправа$\PageIndex{10}$

Вирішити систему шляхом усунення:$\left\{\begin{array}{l}{x^{2}+y^{2}=1} \\ {-x+y^{2}=1}\end{array}\right.$

Відповідь

$(-1,0),(0,1),(0,-1)$

Є також чотири варіанти, коли ми розглядаємо коло і гіперболу.

Приклад$\PageIndex{6}$

Вирішити систему шляхом усунення:$\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.$

Рішення:

Таблиця 11.5.6

Визначте кожен графік.	$\left\{\begin{array}{ll}{x^{2}+y^{2}=7} & {\text { circle }} \\ {x^{2}-y^{2}=1} & {\text { hyperbola }}\end{array}\right.$
Намалюйте можливі варіанти перетину кола і гіперболи.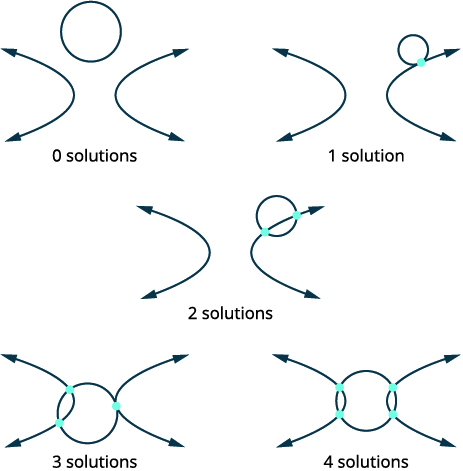
Обидва рівняння мають стандартну форму.	$\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.$
Коефіцієнти$y^{2}$ протилежні, тому ми додамо рівняння.	$\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.$ $2 x^{2}=8$
Спростити.	$x^{2}=4$ $x=\pm 2$ $x=2 \quad x=-2$
Підставити$x=2$ і$x=-2$ в одне з вихідних рівнянь. Тоді вирішуйте для$y$.	$\begin{array}{rl}{x^{2}+y^{2} = 7} &\quad { x^{2}+y^{2}=7} \\ {2^{2}+y^{2}=7} & \quad{(-2)^{2}+y^{2}=7} \\ {4+y^{2}=7} &\quad {4+y^{2}=7} \\ {y^{2}=3} &\quad {y^{2}=3} \\ {y=\pm \sqrt{3}} &\quad {y=\pm \sqrt{3}}\end{array}$
Запишіть кожне рішення як впорядковану пару.	Впорядковані пари є$(-2, \sqrt{3}),(-2,-\sqrt{3})$,$(2, \sqrt{3}),$ і$(2,-\sqrt{3})$.
Переконайтеся, що впорядкована пара є розв'язком обох вихідних рівнянь.
Ми залишимо вам чеки для кожного з чотирьох рішень.	Рішення є$(-2, \sqrt{3}),(-2,-\sqrt{3}),(2, \sqrt{3})$, і$(2,-\sqrt{3})$.

Вправа$\PageIndex{11}$

Вирішити систему шляхом усунення:$\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {y^{2}-x^{2}=7}\end{array}\right.$

Відповідь

$(-3,-4),(-3,4),(3,-4),(3,4)$

Вправа$\PageIndex{12}$

Вирішити систему шляхом усунення:$\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}-y^{2}=4}\end{array}\right.$

Відповідь

$(-2,0),(2,0)$

Використання системи нелінійних рівнянь для розв'язання додатків

Системи нелінійних рівнянь можуть бути використані для моделювання та вирішення багатьох застосувань. На нашому прикладі ми розглянемо повсякденну геометричну ситуацію.

Приклад$\PageIndex{7}$

Різниця квадратів двох чисел дорівнює$15$. Сума чисел дорівнює$5$. Знайдіть цифри.

Рішення:

Таблиця 11.5.7

Визначте, що ми шукаємо.	Два різних числа.
Визначте змінні.	$x$=перше число $y$= друге число
Перевести інформацію в систему рівнянь.
Перше речення.	Різниця квадратів двох чисел дорівнює$15$.
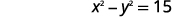Друге речення.	Сума чисел дорівнює$5$.
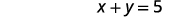Вирішити систему шляхом підміни.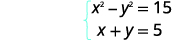
Розв'яжіть друге рівняння для$x$.
$x$Підставляємо в перше рівняння.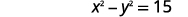
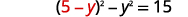Розширюйте і спрощуйте.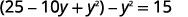
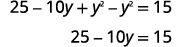Вирішити для$y$.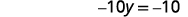
Підставляємо назад у друге рівняння.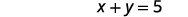
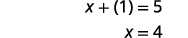	Цифри -$1$ і$4$.

Вправа$\PageIndex{13}$

Різниця квадратів двох чисел дорівнює$−20$. Сума чисел дорівнює$10$. Знайдіть цифри.

Відповідь

$4$і$6$

Вправа$\PageIndex{14}$

Різниця квадратів двох чисел дорівнює$35$. Сума чисел дорівнює$−1$. Знайдіть цифри.

Відповідь

$-18$і$17$

Приклад$\PageIndex{8}$

Майра придбала маленький$25$ «телевізор» для своєї кухні. Розмір телевізора вимірюється по діагоналі екрану. Екран також має площу$300$ квадратних дюймів. Яка довжина і ширина екрану телевізора?

Рішення:

Таблиця 11.5.8

Визначте, що ми шукаємо.	Довжина і ширина прямокутника.
Визначте змінні.	Нехай$x$ = ширина прямокутника $y$= довжина прямокутника
Намалюйте схему, яка допоможе візуалізувати ситуацію.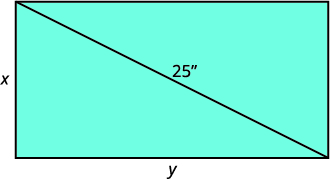
	Площа$300$ квадратних дюймів.
Перевести інформацію в систему рівнянь.	Діагональ прямокутного трикутника дорівнює$25$ дюймам.
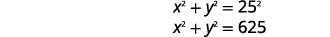	Площа прямокутника -$300$ квадратні дюйми.
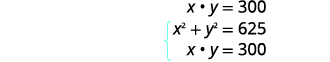Вирішити систему за допомогою підміни.
Розв'яжіть друге рівняння для$x$.
$x$Підставляємо в перше рівняння.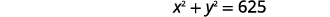
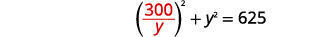Спростити.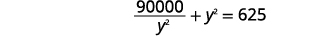
Помножте на$y^{2}$, щоб очистити дроби.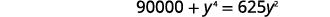
Викладіть в стандартну форму.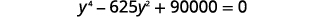
Вирішити шляхом факторингу.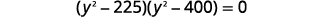
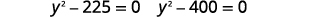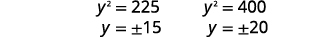Оскільки$y$ це сторона прямокутника, відкидаємо від'ємні значення.
Підставляємо назад у друге рівняння.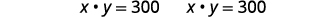
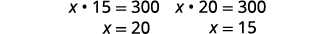	Якщо довжина дорівнює$15$ дюймам, ширина дорівнює$20$ дюймам.
	Якщо довжина дорівнює$20$ дюймам, ширина дорівнює$15$ дюймам.

Вправа$\PageIndex{15}$

Едгар придбав невеликий$20$ «телевізор» для свого гаража. Розмір телевізора вимірюється по діагоналі екрану. Екран також має площу$192$ квадратних дюймів. Яка довжина і ширина екрану телевізора?

Відповідь

Якщо довжина дорівнює$12$ дюймам, ширина дорівнює$16$ дюймам. Якщо довжина дорівнює$16$ дюймам, ширина дорівнює$12$ дюймам.

Вправа$\PageIndex{16}$

Сім'я Харпер придбала невелику мікрохвильовку для своєї сімейної кімнати. Діагональ дверей вимірює$15$ дюйми. Двері також мають площу$108$ квадратних дюймів. Яка довжина і ширина дверцята мікрохвильовки?

Відповідь

Якщо довжина дорівнює$12$ дюймам, ширина дорівнює$9$ дюймам. Якщо довжина дорівнює$9$ дюймам, ширина дорівнює$12$ дюймам.

Отримайте доступ до цих онлайн-ресурсів для отримання додаткових інструкцій та практики розв'язання нелінійних рівнянь.

• Нелінійні системи рівнянь
• Розв'яжіть систему нелінійних рівнянь
• Розв'язування системи нелінійних рівнянь шляхом елімінації
• Система нелінійних рівнянь — застосування площі та периметра

Ключові поняття

• Як розв'язати систему нелінійних рівнянь шляхом побудови графіків.
  1. Визначте графік кожного рівняння. Намалюйте можливі варіанти перетину.
  2. Графік першого рівняння.
  3. Графік другого рівняння на тій же прямокутній системі координат.
  4. Визначте, чи перетинаються графіки.
  5. Визначте точки перетину.
  6. Переконайтеся, що кожна впорядкована пара є розв'язком обох вихідних рівнянь.
• Як розв'язати систему нелінійних рівнянь шляхом підстановки.
  1. Визначте графік кожного рівняння. Намалюйте можливі варіанти перетину.
  2. Розв'яжіть одне з рівнянь для будь-якої змінної.
  3. Підставте вираз з кроку 2 в інше рівняння.
  4. Вирішити отримане рівняння.
  5. Замініть кожне рішення на кроці 4 на одне з вихідних рівнянь, щоб знайти іншу змінну.
  6. Запишіть кожне рішення як впорядковану пару.
  7. Переконайтеся, що кожна впорядкована пара є розв'язком обох вихідних рівнянь.
• Як вирішити систему рівнянь шляхом усунення.
  1. Визначте графік кожного рівняння. Намалюйте можливі варіанти перетину.
  2. Запишіть обидва рівняння в стандартній формі.
  3. Складіть коефіцієнти однієї змінної протилежності.
     Вирішіть, яку змінну ви будете ліквідувати.
     Помножте одне або обидва рівняння так, щоб коефіцієнти цієї змінної були протилежними.
  4. Додайте рівняння, отримані з кроку 3, щоб усунути одну змінну.
  5. Вирішити для залишилася змінної.
  6. Замініть кожне рішення з кроку 5 в одне з вихідних рівнянь. Потім вирішуйте для іншої змінної.
  7. Запишіть кожне рішення як впорядковану пару.
  8. Переконайтеся, що кожна впорядкована пара є розв'язком обох вихідних рівнянь.