6.4: Спеціальні продукти Factor
- Page ID
- 59584
До кінця цього розділу ви зможете:
- Фактор ідеальних квадратних триномів
- Факторні відмінності квадратів
- Факторні суми та відмінності кубів
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Спростити:\((3x^2)^3\).
- Помножити:\((m+4)^2\).
- Помножити:\((x−3)(x+3)\).
Ми бачили, що деякі біноміали та триноми виникають із спеціальних продуктів - квадратних біноміалів та множення кон'югатів. Якщо ви навчитеся розпізнавати такі види поліномів, ви можете використовувати спеціальні шаблони продуктів, щоб набагато швидше їх враховувати.
Фактор Ідеальні квадратні триноми
Деякі триноми є ідеальними квадратами. Вони виникають в результаті множення біноміальних разів на себе. Ми збудували біном у квадраті, використовуючи візерунок Біноміальні квадрати в попередньому розділі.
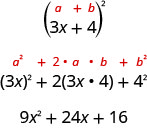
Триноміал\(9x^2+24x+16\) називають досконалим квадратним тріноміалом. Він являє собою квадрат двочлена\(3x+4\).
У цій главі ви почнете з ідеального квадратного триноміала і врахуєте його на прості множники. Ви можете задати цей триноміал за допомогою методів, описаних в останньому розділі, оскільки він має форму\(ax^2+bx+c\). Але якщо ви визнаєте, що перший і останній терміни - квадрати, а триноміал відповідає ідеальному шаблону квадратних триномів, ви заощадите собі багато роботи. Ось візерунок - зворотна частина візерунка біноміальних квадратів.
Якщо\(a\) і\(b\) є дійсними числами
\[a^2+2ab+b^2=(a+b)^2\nonumber\]
\[a^2−2ab+b^2=(a−b)^2\nonumber\]
Щоб скористатися цією схемою, ви повинні визнати, що даний триноміал підходить йому. Перевірте спочатку, щоб побачити, чи провідний коефіцієнт є ідеальним квадратом,\(a^2\). Далі перевірте, що останній термін - ідеальний квадрат,\(b^2\). Потім перевірте середній термін - це продукт,\(2ab\)? Якщо все перевірить, можна легко написати фактори.
Фактор:\(9x^2+12x+4\).
- Відповідь
-



Фактор:\(4x^2+12x+9\).
- Відповідь
-
\((2x+3)^2\)
Фактор:\(9y^2+24y+16\).
- Відповідь
-
\((3y+4)^2\)
Знак середнього члена визначає, який візерунок ми будемо використовувати. Коли середній термін негативний, ми використовуємо патерн\(a^2−2ab+b^2\), який чинники для\((a−b)^2\).
Кроки підсумовуються тут.
\(\begin{array} {lllll} \textbf{Step 1.} &\text{Does the trinomial fit the pattern?} &\quad &\hspace{7mm} a^2+2ab+b^2 &\hspace{7mm} a^2−2ab+b^2 \\ &\text{Are the first and last terms perfect squares?} &\quad & &\\ &\text{Write them as squares.} &\quad &\hspace{5mm}(a)^2\hspace{16mm} (b)^2 &\hspace{6mm}(a)^2\hspace{16mm} (b)^2 \\ &\text{Check the middle term. Is it }2ab? &\quad &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} \\ \textbf{Step 2.} &\text{Write the square of the binomial.} &\quad &\hspace{13mm} (a+b)^2 &\hspace{13mm} (a−b)^2 \\ \textbf{Step 3.} &\text{Check by multiplying.} & & & \end{array}\)
Ми будемо працювати зараз, де середній термін є негативним.
Фактор:\(81y^2−72y+16\).
- Відповідь
-
Перший і останній члени - квадрати. Подивіться, чи відповідає середній термін візерунку ідеального квадратного трінома. Середній термін негативний, тому біноміальний квадрат буде\((a−b)^2\).
\(81 y^{2}-72 y+16\) Перші та останні терміни ідеальні квадрати? 
Перевірте середній термін. 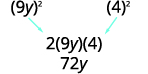
Чи відповідає це\((a−b)^2\)? Так. 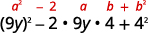
Пишіть як квадрат двочлена. \((9 y-4)^{2}\) Перевірте, перемноживши:
\[(9y−4)^2\nonumber\]\[(9y)^2−2·9y·4+4^2\nonumber\]\[81y^2−72y+16\checkmark\nonumber\]
Фактор:\(64y^2−80y+25\).
- Відповідь
-
\((8y−5)^2\)
Фактор:\(16z^2−72z+81\).
- Відповідь
-
\((4z−9)^2\)
Наступним прикладом буде ідеальний квадратний тріноміал з двома змінними.
Фактор:\(36x^2+84xy+49y^2\).
- Відповідь
-
\(36 x^{2}+84 x y+49 y^{2}\) Перевірте кожен термін, щоб перевірити візерунок. 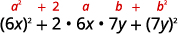
Фактор. \((6 x+7 y)^{2}\) Перевірка шляхом множення.
\[(6x+7y)^2\nonumber\]\[(6x)^2+2·6x·7y+(7y)^2\nonumber\]\[36x^2+84xy+49y^2\checkmark\nonumber\]
Фактор:\(49x^2+84xy+36y^2\).
- Відповідь
-
\((7x+6y)^2\)
Фактор:\(64m^2+112mn+49n^2\).
- Відповідь
-
\((8m+7n)^2\)
Пам'ятайте, що перший крок у факторингу полягає в тому, щоб шукати найбільший загальний фактор. Ідеальні квадратні триноми можуть мати GCF у всіх трьох термінів, і це повинно бути враховано в першу чергу. І, іноді, як тільки GCF був врахований, ви визнаєте ідеальний квадратний триноміал.
Фактор:\(100x^2y−80xy+16y\).
- Відповідь
-
\(100 x^{2} y-80 x y+16 y\) Чи є GCF? Так\(4y\), так що фактор це. \(4 y\left(25 x^{2}-20 x+4\right)\) Це ідеальний квадратний триноміал? Перевірте викрійку. 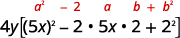
Фактор. \(4 y(5 x-2)^{2}\) Пам'ятайте: зберігайте коефіцієнт 4 y в кінцевому продукті. Перевірка:
\[4y(5x−2)^2\nonumber\]\[4y[(5x)2−2·5x·2+22]\nonumber\]\[4y(25x2−20x+4)\nonumber\]100x2y−80xy+16y\ галочка\]
Фактор:\(8x^2y−24xy+18y\).
- Відповідь
-
\(2y(2x−3)^2\)
Фактор:\(27p^2q+90pq+75q\).
- Відповідь
-
\(3q(3p+5)^2\)
Факторні відмінності квадратів
Іншим спеціальним продуктом, який ви бачили в попередньому розділі, був візерунок «Продукт кон'югатів». Ви використовували це, щоб помножити два двочлени, які були сполученими. Ось приклад:
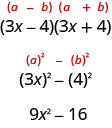
Різниця квадратів коефіцієнтів на добуток кон'югатів.
Якщо\(a\) і\(b\) є дійсними числами,
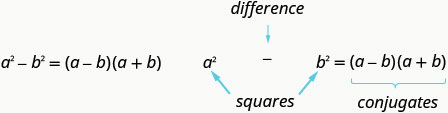
Пам'ятайте, «різниця» відноситься до віднімання. Отже, щоб використовувати цей візерунок, ви повинні переконатися, що у вас є біноміал, в якому віднімаються два квадрати.
Фактор:\(64y^2−1\).
- Відповідь
-




Фактор:\(121m^2−1\).
- Відповідь
-
\((11m−1)(11m+1)\)
Фактор:\(81y^2−1\).
- Відповідь
-
\((9y−1)(9y+1)\)
\(\begin{array} {llll} \textbf{Step 1.} &\text{Does the binomial fit the pattern?} &\qquad &\hspace{5mm} a^2−b^2 \\ &\text{Is this a difference?} &\qquad &\hspace{2mm} \text{____−____} \\ &\text{Are the first and last terms perfect squares?} & & \\ \textbf{Step 2.} &\text{Write them as squares.} &\qquad &\hspace{3mm} (a)^2−(b)^2 \\ \textbf{Step 3.} &\text{Write the product of conjugates.} &\qquad &(a−b)(a+b) \\ \textbf{Step 4.} &\text{Check by multiplying.} & & \end{array}\)
Важливо пам'ятати, що суми квадратів не враховуються на добуток біноміалів. Не існує біноміальних факторів, які множаться разом, щоб отримати суму квадратів. Після видалення будь-якого GCF вираз\(a^2+b^2\) є простим!
Наступний приклад показує змінні в обох термінях.
Фактор:\(144x^2−49y^2\).
- Відповідь
-
\(\begin{array} {lll} &\quad &144x^2−49y^2 \\ \text{Is this a difference of squares? Yes.} &\quad &(12x)^2−(7y)^2 \\ \text{Factor as the product of conjugates.} &\quad &(12x−7y)(12x+7y) \\ \text{Check by multiplying.} &\quad &(12x−7y)(12x+7y) \\ \text{Check by multiplying.} &\quad & \\ &\quad & \\ &\quad & \\ \hspace{14mm} (12x−7y)(12x+7y) &\quad & \\ \hspace{21mm} 144x^2−49y^2\checkmark &\quad & \end{array}\)
Фактор:\(196m^2−25n^2\).
- Відповідь
-
\((14m−5n)(14m+5n)\)
Фактор:\(121p^2−9q^2\).
- Відповідь
-
\((11p−3q)(11p+3q)\)
Як завжди, спочатку слід шукати загальний фактор, коли у вас є вираз для фактора. Іноді загальний фактор може «замаскувати» різницю квадратів, і ви не розпізнаєте ідеальні квадрати, поки не вважатимете GCF.
Крім того, щоб повністю врахувати біноміальне в наступному прикладі, ми розглянемо різницю квадратів двічі!
Фактор:\(48x^4y^2−243y^2\).
- Відповідь
-
\(\begin{array} {ll} &48x^4y^2−243y^2 \\ \text{Is there a GCF? Yes, }3y^2\text{—factor it out!} &3y^2(16x^4−81) \\ \text{Is the binomial a difference of squares? Yes.} &3y^2\left((4x^2)^2−(9)^2\right) \\ \text{Factor as a product of conjugates.} &3y^2(4x^2−9)(4x^2+9) \\ \text{Notice the first binomial is also a difference of squares!} &3y^2((2x)^2−(3)^2)(4x^2+9) \\ \text{Factor it as the product of conjugates.} &3y^2(2x−3)(2x+3)(4x^2+9) \end{array}\)
Останній множник, сума квадратів, не може бути врахований.
\(\begin{array} {l} \text{Check by multiplying:} \\ \hspace{10mm} 3y^2(2x−3)(2x+3)(4x^2+9) \\ \\ \\ \hspace{15mm} 3y^2(4x^2−9)(4x^2+9) \\ \hspace{20mm} 3y^2(16x^4−81) \\ \hspace{19mm} 48x^4y^2−243y^2\checkmark\end{array}\)
Фактор:\(2x^4y^2−32y^2\).
- Відповідь
-
\(2y^2(x−2)(x+2)(x^2+4)\)
Фактор:\(7a^4c^2−7b^4c^2\).
- Відповідь
-
\(7c^2(a−b)(a+b)(a^2+b^2)\)
Наступний приклад має многочлен з 4 членами. Поки що, коли це сталося, ми групували терміни по два і враховували звідти. Тут ми помітимо, що перші три члени утворюють ідеальний квадратний триноміал.
Фактор:\(x^2−6x+9−y^2\).
- Відповідь
-
Зверніть увагу, що перші три члени утворюють ідеальний квадратний триноміал.
\(x^{2}-6 x+9-y^{2}\) Фактор шляхом групування перших трьох термінів. \(\underbrace{x^{2}-6 x+9} - y^{2}\) Використовуйте ідеальний квадратний тріноміальний візерунок. \((x-3)^{2}-y^{2}\) Це різниця квадратів? Так. Так—запишіть їх як квадрати. 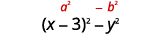
Фактор як добуток кон'югатів. 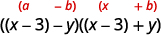
\((x-3-y)(x-3+y)\) Можливо, ви захочете переписати рішення як\((x−y−3)(x+y−3)\).
Фактор:\(x^2−10x+25−y^2\).
- Відповідь
-
\((x−5−y)(x−5+y)\)
Фактор:\(x^2+6x+9−4y^2\).
- Відповідь
-
\((x+3−2y)(x+3+2y)\)
Факторні суми та відмінності кубів
Існує ще один спеціальний шаблон факторингу, той, який ми не використовували, коли ми множили многочлени. Це шаблон для суми і різниці кубиків. Ми спочатку напишемо ці формули, а потім перевіримо їх множенням.
\[a^3+b^3=(a+b)(a^2−ab+b^2\nonumber\]
\[a^3−b^3=(a−b)(a^2+ab+b^2)\nonumber\]
Перевіримо першу викрійку, а другу залишимо вам.
| \(\color{red}(a+b) \color{black} \left(a^{2}-a b+b^{2}\right)\) | |
| Розподілити. | \(\color{red}a \color{black}\left(a^{2}-a b+b^{2}\right)+ \color{red}b \color{black}\left(a^{2}-a b+b^{2}\right)\) |
| Помножити. | \(a^{3}-a^{2} b+a b^{2}+a^{2} b-a b^{2}+b^{3}\) |
| Поєднуйте подібні терміни. | \(a^{3}+b^{3}\) |
\[a^3+b^3=(a+b)(a^2−ab+b^2\nonumber\]\[a^3−b^3=(a−b)(a^2+ab+b^2)\nonumber\]
Два візерунки виглядають дуже схожими, чи не так? Але зверніть увагу на ознаки в факторах. Знак біноміального фактора збігається зі знаком в початковому біном. А знак середнього члена триноміального фактора протилежний знаку в початковому біноміальному. Якщо ви розпізнаєте закономірність знаків, це може допомогти вам запам'ятати візерунки.

Триноміальний коефіцієнт у сумі та різниці кубиків не може бути врахований.
Буде дуже корисно, якщо ви навчитеся розпізнавати кубики цілих чисел від 1 до 10, так само, як ви навчилися розпізнавати квадрати. Ми перерахували куби цілих чисел від 1 до 10 в табл.
| п | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(n^3\) | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1000 |
Фактор:\(x^3+64\).
- Відповідь
-





Фактор:\(x^3+27\).
- Відповідь
-
\((x+3)(x^2−3x+9)\)
Фактор:\(y^3+8\).
- Відповідь
-
\((y+2)(y^2−2y+4)\)
- Чи підходить біноміал до суми чи різниці кубиків?
Це сума чи різниця?
Перші та останні терміни ідеальні кубики? - Запишіть їх у вигляді кубиків.
- Використовуйте або суму, або різницю кубиків.
- Спростити всередині дужок.
- Перевірте, множивши коефіцієнти.
Фактор:\(27u^3−125v^3\).
- Відповідь
-
\(27 u^{3}-125 v^{3}\) Цей біноміал є різницею. Перший і останній
терміни - ідеальні кубики.Запишіть терміни у вигляді кубиків. 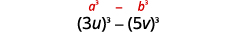
Скористайтеся різницею кубиків візерунком. 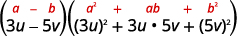
Спростити. 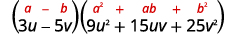
Перевірка шляхом множення. Ми залишимо чек вам.
Фактор:\(8x^3−27y^3\).
- Відповідь
-
\((2x−3y)(4x^2+6xy+9y^2)\)
Фактор:\(1000m^3−125n^3\).
- Відповідь
-
\((10m−5n)(100m^2+50mn+25n^2)\)
У наступному прикладі ми спочатку враховуємо GCF. Тоді ми можемо розпізнати суму кубів.
Фактор:\(6x^3y+48y^4\).
- Відповідь
-
\(6 x^{3} y+48 y^{4}\) Фактор загальний фактор. \(6 y\left(x^{3}+8 y^{3}\right)\) Цей біноміал є сумою Перший і останній члени
- ідеальні кубики.Запишіть терміни у вигляді кубиків. 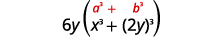
Використовуйте шаблон суми кубиків. 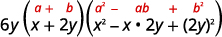
Спростити. 
Перевірка:
Щоб перевірити, вам може бути простіше спочатку помножити суму коефіцієнтів кубів, а потім помножити цей продукт на 6y.6y. Ми залишимо множення для вас.
Фактор:\(500p^3+4q^3\).
- Відповідь
-
\(4(5p+q)(25p^2−5pq+q^2)\)
Фактор:\(432c^3+686d^3\).
- Відповідь
-
\(2(6c+7d)(36c^2−42cd+49d^2)\)
Перший член в наступному прикладі - це біноміальний куб.
Фактор:\((x+5)^3−64x^3\).
- Відповідь
-
\((x+5)^{3}-64 x^{3}\) Цей біноміал є різницею. Перший і
останній терміни - ідеальні кубики.Запишіть терміни у вигляді кубиків. 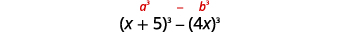
Скористайтеся різницею кубиків візерунком. 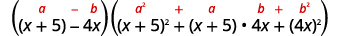
Спростити. \((x+5-4 x)\left(x^{2}+10 x+25+4 x^{2}+20 x+16 x^{2}\right)\) \((-3 x+5)\left(21 x^{2}+30 x+25\right)\) Перевірка шляхом множення. Ми залишимо чек вам.
Фактор:\((y+1)^3−27y^3\).
- Відповідь
-
\((−2y+1)(13y^2+5y+1)\)
Фактор:\((n+3)^3−125n^3\).
- Відповідь
-
\((−4n+3)(31n^2+21n+9)\)
Отримайте доступ до цього інтернет-ресурсу для додаткової інструкції та практики з факторинговими спеціальними продуктами.
Ключові концепції
- досконалий квадрат тріноми візерунком: якщо а і б є дійсними числами,
\[\begin{array} {l} a^2+2ab+b^2=(a+b)^2 \\ a^2−2ab+b^2=(a−b)^2\end{array} \nonumber\]
- Як врахувати ідеальні квадратні триноми.
\(\begin{array} {lllll} \textbf{Step 1.} &\text{Does the trinomial fit the pattern?} &\quad &\hspace{7mm} a^2+2ab+b^2 &\hspace{7mm} a^2−2ab+b^2 \\ &\text{Are the first and last terms perfect squares?} &\quad & &\\ &\text{Write them as squares.} &\quad &\hspace{5mm}(a)^2\hspace{16mm} (b)^2 &\hspace{6mm}(a)^2\hspace{16mm} (b)^2 \\ &\text{Check the middle term. Is it }2ab? &\quad &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} \\ \textbf{Step 2.} &\text{Write the square of the binomial.} &\quad &\hspace{13mm} (a+b)^2 &\hspace{13mm} (a−b)^2 \\ \textbf{Step 3.} &\text{Check by multiplying.} & & & \end{array}\) - Різниця квадратів візерунком: якщо a, ba, b є дійсними числами,
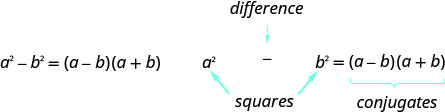
- Як врахувати відмінності квадратів.
\(\begin{array} {llll} \textbf{Step 1.} &\text{Does the binomial fit the pattern?} &\qquad &\hspace{5mm} a^2−b^2 \\ &\text{Is this a difference?} &\qquad &\hspace{2mm} \text{____−____} \\ &\text{Are the first and last terms perfect squares?} & & \\ \textbf{Step 2.} &\text{Write them as squares.} &\qquad &\hspace{3mm} (a)^2−(b)^2 \\ \textbf{Step 3.} &\text{Write the product of conjugates.} &\qquad &(a−b)(a+b) \\ \textbf{Step 4.} &\text{Check by multiplying.} & & \end{array}\) - Сума та різниця кубів
\(\begin{array} {l} a^3+b3=(a+b)(a^2−ab+b^2) \\ a^3−b^3=(a−b)(a^2+ab+b^2) \end{array} \) - Як коефіцієнт суми або різниці кубів.
- Чи підходить біноміал до суми чи різниці кубиків?
Це сума чи різниця?
Перші та останні терміни ідеальні кубики? - Запишіть їх у вигляді кубиків.
- Використовуйте або суму, або різницю кубиків.
- Спрощення всередині дужок
- Перевірте, множивши коефіцієнти.
- Чи підходить біноміал до суми чи різниці кубиків?
