6.3E: Вправи

Last updated
Save as PDF

Page ID: 59553

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Практика робить досконалим

Факторні триміали форми$x^2+bx+c$

У наступних вправах враховуйте кожен триноміал форми$x^2+bx+c$.

1. $p^2+11p+30$

Відповідь: $(p+5)(p+6)$

2. $w^2+10w+21$

3. $n^2+19n+48$

Відповідь: $(n+3)(n+16)$

4. $b^2+14b+48$

5. $a^2+25a+100$

Відповідь: $(a+5)(a+20)$

6. $u^2+101u+100$

7. $x^2−8x+12$

Відповідь: $(x−2)(x−6)$

8. $q^2−13q+36$

9. $y^2−18y+45$

Відповідь: $(y−3)(y−15)$

10. $m^2−13m+30$

11. $x^2−8x+7$

Відповідь: $(x−1)(x−7)$

12. $y^2−5y+6$

13. $5p−6+p^2$

Відповідь: $(p−1)(p+6)$

14. $6n−7+n^2$

15. $8−6x+x^2$

Відповідь: $(x−4)(x−2)$

16. $7x+x^2+6$

17. $x^2−12−11x$

Відповідь: $(x−12)(x+1)$

18. $−11−10x+x^2$

У наступних вправах враховуйте кожен триноміал форми$x^2+bxy+cy^2$.

19. $x^2−2xy−80y^2$

Відповідь: $(x+8y)(x−10y)$

20. $p^2−8pq−65q^2$

21. $m^2−64mn−65n^2$

Відповідь: $(m+n)(m−65n)$

22. $p^2−2pq−35q^2$

23. $a^2+5ab−24b^2$

Відповідь: $(a+8b)(a−3b)$

24. $r^2+3rs−28s^2$

25. $x^2−3xy−14y^2$

Відповідь: Прем'єр

26. $u^2−8uv−24v^2$

27. $m^2−5mn+30n^2$

Відповідь: Прем'єр

28. $c^2−7cd+18d^2$

Факторні тріноми форми з$ax^2+bx+c$ використанням проб і помилок

У наступних вправах фактор повністю за допомогою проб і помилок.

29. $p^3−8p^2−20p$

Відповідь: $p(p−10)(p+2)$

30. $q^3−5q^2−24q$

31. $3m^3−21m^2+30m$

Відповідь: $3m(m−5)(m−2)$

32. $11n^3−55n^2+44n$

33. $5x^4+10x^3−75x^2$

Відповідь: $5x^2(x−3)(x+5)$

34. $6y^4+12y^3−48y^2$

35. $2t^2+7t+5$

Відповідь: $(2t+5)(t+1)$

36. $5y^2+16y+11$

37. $11x^2+34x+3$

Відповідь: $(11x+1)(x+3)$

38. $7b^2+50b+7$

39. $4w^2−5w+1$

Відповідь: $(4w−1)(w−1)$

40. $5x^2−17x+6$

41. $4q^2−7q−2$

Відповідь: $(4q+1)(q−2)$

42. $10y^2−53y−111$

43. $6p^2−19pq+10q^2$

Відповідь: $(2p−5q)(3p−2q)$

44. $21m^2−29mn+10n^2$

45. $4a^2+17ab−15b^2$

Відповідь: $(4a−3b)(a+5b)$

46. $6u^2+5uv−14v^2$

47. $−16x^2−32x−16$

Відповідь: $−16(x+1)(x+1)$

48. $−81a^2+153a+18$

49. $−30q^3−140q^2−80q$

Відповідь: $ - 10q(3q+2)(q+4)$

50. $−5y^3−30y^2+35y$

Факторні тріноми форми$ax^2+bx+c$ методом 'ac'

У наступних вправах фактор за допомогою методу «ac».

51. $5n^2+21n+4$

Відповідь: $(5n+1)(n+4)$

52. $8w^2+25w+3$

53. $4k^2−16k+15$

Відповідь: $(2k−3)(2k−5)$

54. $5s^2−9s+4$

55. $6y^2+y−15$

Відповідь: $(3y+5)(2y−3)$

56. $6p^2+p−22$

57. $2n^2−27n−45$

Відповідь: $(2n+3)(n−15)$

58. $12z^2−41z−11$

59. $60y^2+290y−50$

Відповідь: $10(6y−1)(y+5)$

60. $6u^2−46u−16$

61. $48z^3−102z^2−45z$

Відповідь: $3z(8z+3)(2z−5)$

62. $90n^3+42n^2−216n$

63. $16s^2+40s+24$

Відповідь: $8(2s+3)(s+1)$

64. $24p^2+160p+96$

65. $48y^2+12y−36$

Відповідь: $12(4y−3)(y+1)$

66. $30x^2+105x−60$

Фактор, що використовує підстановку

У наступних вправах враховуєтьсяфактор за допомогою заміщення.

67. $x^4−x^2−12$

Відповідь: $(x^2+3)(x^2−4)$

68. $x^4+2x^2−8$

69. $x^4−3x^2−28$

Відповідь: $(x^2−7)(x^2+4)$

70. $x^4−13x^2−30$

71. $(x−3)^2−5(x−3)−36$

Відповідь: $(x−12)(x+1)$

72. $(x−2)^2−3(x−2)−54$

73. $(3y−2)^2−(3y−2)−2$

Відповідь: $(3y−4)(3y−1)$

74. $(5y−1)^2−3(5y−1)−18$

Змішана практика

У наступних вправах враховуйте кожен вираз за допомогою будь-якого методу.

75. $u^2−12u+36$

Відповідь: $(u−6)(u−6)$

76. $x^2−14x−32$

77. $r^2−20rs+64s^2$

Відповідь: $(r−4s)(r−16s)$

78. $q^2−29qr−96r^2$

79. $12y^2−29y+14$

Відповідь: $(4y−7)(3y−2)$

80. $12x^2+36y−24z$

81. $6n^2+5n−4$

Відповідь: $(2n−1)(3n+4)$

82. $3q^2+6q+2$

83. $13z^2+39z−26$

Відповідь: $13(z^2+3z−2)$

84. $5r^2+25r+30$

85. $3p^2+21p$

Відповідь: $3p(p+7)$

86. $7x^2−21x$

87. $6r^2+30r+36$

Відповідь: $6(r+2)(r+3)$

88. $18m^2+15m+3$

89. $24n^2+20n+4$

Відповідь: $4(2n+1)(3n+1)$

90. $4a^2+5a+2$

91. $x^4−4x^2−12$

Відповідь: $(x^2+2)(x^2−6)$

92. $x^4−7x^2−8$

93. $(x+3)^2−9(x+3)−36$

Відповідь: $(x−9)(x+6)$

94. $(x+2)^2−25(x+2)−54$

Письмові вправи

95. Багато триноми$x^2+bx+c$ форм-фактора в добуток двох біноміалів$(x+m)(x+n)$. Поясніть, як ви знаходите значення$m$ і$n$.

Відповідь: Відповіді будуть відрізнятися.

96. Томмі заробив$x^2−x−20$ як$(x+5)(x−4)$. Сара заробила це як$(x+4)(x−5)$. Ернесто заробив це як$(x−5)(x−4)$. Хто правий? Поясніть, чому інші два помиляються.

97. Перелічіть, по порядку, всі кроки, які ви робите при використанні методу «$ac$», щоб зарахувати тріноміал форми$ax^2+bx+c$.

Відповідь: Відповіді будуть відрізнятися.

98. Як метод «$ac$» схожий на метод «скасувати FOIL»? Чим вона відрізняється?

Самостійна перевірка

а Після виконання вправ скористайтеся цим контрольним списком, щоб оцінити своє володіння цілями цього розділу.

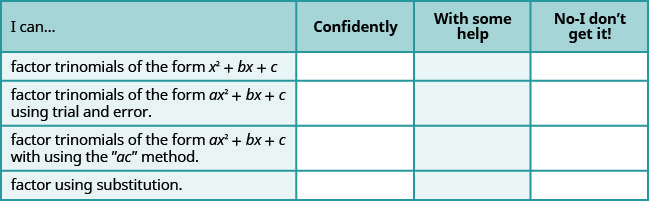
$Ця таблиця має 4 стовпці, 4 рядки та рядок заголовка. Рядок заголовка позначає кожен стовпець: я можу, впевнено, з деякою допомогою і ні, я цього не отримую. Перший стовпець має такі твердження: факторні тріноми виду x в квадраті плюс bx плюс c, множники виду a x в квадраті плюс b x плюс c за допомогою проб і помилок, множники фактора виду a x в квадраті плюс bx плюс c з використанням методу «ac», коефіцієнт з використанням підстановки.$

б Ознайомившись з цим контрольним списком, що ви будете робити, щоб стати впевненими у всіх цілях?