5.5: Ділильні многочлени

Last updated
Save as PDF

Page ID: 59528

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

До кінця цього розділу ви зможете:

ділильні мономи
Ділення многочлена на моном
Ділильні многочлени з використанням довгого ділення
Ділення многочленів за допомогою синтетичного ділення
Функції, що ділять многочлени
Використовуйте теореми про залишок і множник

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

Додати:$\dfrac{3}{d}+\dfrac{x}{d}$.
Якщо ви пропустили цю проблему, перегляньте [посилання].
Спростити:$\dfrac{30xy}{35xy}$.
Якщо ви пропустили цю проблему, перегляньте [посилання].
Поєднуйте подібні терміни:$8a^2+12a+1+3a^2−5a+4$.
Якщо ви пропустили цю проблему, перегляньте [посилання].

Поділ мономи

Зараз ми знайомі з усіма властивостями експонент і використовували їх для множення многочленів. Далі ми будемо використовувати ці властивості, щоб розділити мономи і поліноми.

Приклад$\PageIndex{1}$

Знайдіть частку:$54a^2b^3÷ (−6ab^5)$.

Рішення

Коли ми ділимо мономіали з більш ніж однією змінною, ми пишемо один дріб для кожної змінної.

$\begin{array} {ll} {} &{54a^2b^3÷(−6ab^5)} \\[5pt] {\text{Rewrite as a fraction.}} &{\dfrac{54a^2b^3}{−6ab^5}} \\[5pt] {\text{Use fraction multiplication.}} &{\dfrac{54}{−6}·\dfrac{a^2}{a}·\dfrac{b^3}{b^5}} \\[5pt] {\text{Simplify and use the Quotient Property.}} &{−9·a·\dfrac{1}{b^2}} \\[5pt] {\text{Multiply.}} &{−\dfrac{9a}{b^2}} \end{array}$

Спробуйте! $\PageIndex{1}$

Знайдіть частку:$−72a^7b^3÷(8a^{12}b^4)$.

Відповідь: $−\dfrac{9}{a^5b}$

Спробуйте! $\PageIndex{2}$

Знайдіть частку:$−63c^8d^3÷(7c^{12}d^2)$.

Відповідь: $\dfrac{−9d}{c^4}$

Після того, як ви ознайомитеся з процесом і практикуєте його крок за кроком кілька разів, ви можете спростити частку за один крок.

Приклад$\PageIndex{2}$

Знайдіть частку:$\dfrac{14x^7y^{12}}{21x^{11}y^6}$.

Рішення

Будьте дуже обережні, щоб спростити,$\dfrac{14}{21}$ розділивши загальний коефіцієнт, і спростити змінні, віднімаючи їх показники.

$\begin{array} {ll} {} &{\dfrac{14x^7y^{12}}{21x^{11}y^6}} \\ {\text{Simplify and use the Quotient Property.}} &{\dfrac{2y^6}{3x^4}} \\ \end{array}$

Спробуйте! $\PageIndex{3}$

Знайдіть частку:$\dfrac{28x^5y^{14}}{49x^9y^{12}}$.

Відповідь: $\dfrac{4y^2}{7x^4}$

Спробуйте! $\PageIndex{4}$

Знайдіть частку:$\dfrac{30m^5n^{11}}{48m^{10}n^{14}}$.

Відповідь: $\dfrac{5}{8m^5n^3}$

Розділити многочлен на мономіал

Тепер, коли ми знаємо, як розділити мономіал на мономіал, наступна процедура полягає в тому, щоб розділити многочлен з двох або більше членів на мономіал. Метод, який ми будемо використовувати для поділу многочлена на мономіал, заснований на властивостях додавання дробів. Таким чином, ми почнемо з прикладу для перегляду додавання дробу. Сума$\dfrac{y}{5}+\dfrac{2}{5}$ спрощує$\dfrac{y+2}{5}$. Тепер ми зробимо це в зворотному порядку, щоб розділити один дріб на окремі дроби. Наприклад,$\dfrac{y+2}{5}$ може бути написаний$\dfrac{y}{5}+\dfrac{2}{5}$.

Це «зворотне» додавання дробу, і він стверджує, що якщо a, b і c - числа де$c\neq 0$, то$\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}$. Ми будемо використовувати це, щоб розділити многочлени на мономи.

Означення: ДІЛЕННЯ ПОЛІНОМА НА МОНОМІАЛ

Щоб розділити многочлен на мономіал, розділіть кожен член многочлена на моном.

Приклад$\PageIndex{3}$

Знайдіть частку:$(18x^3y−36xy^2)÷(−3xy)$.

Рішення

$\begin{array} {ll} {} &{(18x^3y−36xy^2)÷(−3xy)} \\[5pt] {\text{Rewrite as a fraction.}} &{\dfrac{18x^3y−36xy^2}{−3xy}} \\[5pt] {\text{Divide each term by the divisor. Be careful with the signs!}} &{\dfrac{18x^3y}{−3xy}−\dfrac{36xy^2}{−3xy}} \\[5pt] {\text{Simplify.}} &{−6x^2+12y} \end{array}$

Спробуйте! $\PageIndex{5}$

Знайдіть частку:$(32a^2b−16ab^2)÷(−8ab)$.

Відповідь: $−4a+2b$

Спробуйте! $\PageIndex{6}$

Знайдіть частку:$(−48a^8b^4−36a^6b^5)÷(−6a^3b^3)$.

Відповідь: $8a^5b+6a^3b^2$

Розділити многочлени за допомогою довгого ділення

Розділивши многочлен на біноміал, дотримуємося процедури, дуже схожою на довге ділення чисел. Отже, давайте уважно розглянемо кроки, які ми робимо, коли ми ділимо 3-значне число, 875, на 2-значне число, 25.

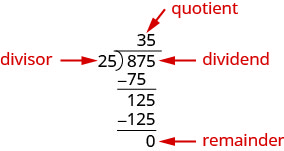
$На цьому малюнку показано довге ділення 875 ділиться на 25. 875 позначається дивідендом, а 25 позначено дільником. Результат 35 позначається коефіцієнтом. 3 в 35 визначається з кількості разів ми можемо розділити 25 на 87. Множення 25 і 3 призводить до 75. 75 віднімається з 87, щоб отримати 12. 5 з 875 опускається вниз, щоб зробити 12 в 125. 5 в 35 визначається з кількості разів можна розділити 25 на 125. Оскільки 25 переходить у 125 рівномірно, залишку немає. Результат віднімання 125 з 125 дорівнює 0, який позначений залишком.$

Перевіряємо ділення множенням частки на дільник. Якщо ми зробили поділ правильно, продукт повинен дорівнювати дивідендам.

\[\begin{array} {l} {35·25} \\ {875\checkmark} \\ \nonumber \end{array}\]

Тепер розділимо тріноміал на біноміал. Коли ви читаєте приклад, зверніть увагу, наскільки кроки схожі на числовий приклад вище.

Приклад$\PageIndex{4}$

Знайдіть частку:$(x^2+9x+20)÷(x+5)$.

Рішення

$\require{enclose}$	$\qquad (x^2+9x+20) \div (x+5)$
Напишіть це як довгу проблему поділу. Переконайтеся, що дивіденди в стандартній формі.	$\qquad x+5\enclose{longdiv}{ x^2+9x+20\phantom{0}} $
Розділити$x^2$ на$x$. Це може допомогти запитати себе: «На що мені потрібно $x$ помножити, щоб отримати$x^2$?»	$\qquad \begin{array}{r} {\color{red}x}\hspace{2.3em}\\[-3pt] {\color{red}x}+5\enclose{longdiv}{ {\color{red}x^2}+9x+20\phantom{0}} \end{array}$
Поставте відповідь$x$, в частку над$x$ терміном. Множимо$x$ раз$x+5$. Вибудовуйте подібні умови під дивідендами.	$\qquad \begin{array}{r}x\hspace{2.3em}\\[-3pt] x+5\enclose{longdiv}{x^2+9x+20\phantom{0}}\\[-3pt] \underline{\color{red}x^2+5x}\hspace{2.4em} \end{array}$
Відняти$x^2+5x$ від$x^2+9x$. Можливо, вам буде легше змінити знаки, а потім додати. Потім збити останній термін,$20.$	$\qquad \begin{array}{r}x\hspace{2.3em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] {\color{red}4x+20}\hspace{0.5em} \end{array}$
Розділити$4x$ на$x$. Це може допомогти запитати себе: «На що мені потрібно$x$ помножити, щоб отримати$4x$?» Поставте відповідь$4$, в частку над постійним терміном.	$\qquad \begin{array}{r}x+\phantom{0}{\color{red}4}\hspace{.5em}\\[-3pt] {\color{red}x}+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] {\color{red}4x}+20\hspace{0.5em} \end{array}$
Помножте 4 рази$x+5$.	$\qquad \begin{array}{r}x+\phantom{0}4\hspace{.5em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] 4x+20\hspace{0.5em}\\[-3pt] \underline{ \color{red}4x+20}\hspace{.5em} \end{array}$
Відняти$4x+20$ від$4x+20$.	$\qquad \begin{array}{r}x+\phantom{0}4\hspace{.5em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] 4x+20\hspace{.5em}\\[-3pt] \underline{{\color{red}-}4x+({\color{red}-}20)}\\[-3pt] 0\hspace{.33em}\end{array}$
Перевірка: $\begin{array} {ll} {\text{Multiply the quotient by the divisor.}} &{(x+4)(x+5)} \\ {\text{You should get the dividend.}} &{x^2+9x+20\checkmark}\\ \end{array}$

Спробуйте! $\PageIndex{7}$

Знайдіть частку:$(y^2+10y+21)÷(y+3)$.

Відповідь: $y+7$

Спробуйте! $\PageIndex{8}$

Знайдіть частку:$(m^2+9m+20)÷(m+4)$.

Відповідь: $m+5$

Коли ми розділили 875 на 25, у нас не було залишку. Але іноді ділення чисел залишає залишок. Те ж саме відбувається, коли ми ділимо многочлени. У наступному прикладі ми будемо мати поділ, який залишає залишок. Запишемо залишок у вигляді дробу з дільником як знаменником.

Озирніться назад на дивіденди в попередніх прикладах. Терміни писалися в порядку убування ступенів, і відсутніх ступенів не було. Дивіденд в цьому прикладі буде$x^4−x^2+5x−6$. У ньому відсутній$x^3$ термін. Ми додамо в$0x^3$ якості заповнювача.

Приклад$\PageIndex{5}$

Знайдіть частку:$(x^4−x^2+5x−6)÷(x+2)$.

Рішення

Зверніть увагу, що в дивіденді немає$x^3$ терміну. Ми додамо$0x^3$ як заповнювач.

	$.$
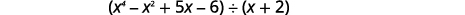Напишіть це як довгу проблему поділу. Переконайтеся, що дивіденди в стандартній формі з заповнювачами для відсутніх термінів.	$.$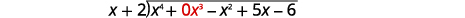
Розділити$x^4$ на$x$. Поставте відповідь$x^3$, в частку над$x^3$ терміном. Множимо$x^3$ раз$x+2$. Вибудовуйте подібні терміни. Відніміть, а потім збийте наступний термін.	$.$
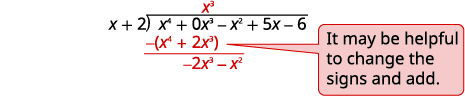Розділити$−2x^3$ на$x$. Поставте відповідь$−2x^2$, в частку над$x^2$ терміном. Множимо$−2x^2$ раз$x+1$. Вибудовуйте подібні терміни Відніміть і збийте наступний термін.	$.$
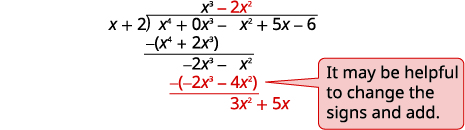Розділити$3x^2$ на$x$. Поставте відповідь$3x$, в частку над$x$ терміном. Множимо$3x$ раз$x+1$. Вибудовуйте подібні терміни. Відніміть і збийте наступний термін.	$.$
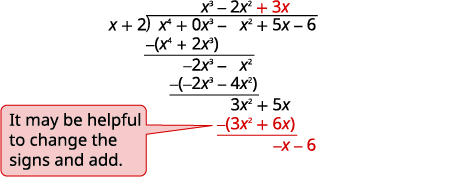Розділити$−x$ на$x$. Поставте відповідь$−1$, в частку над постійним терміном. Множимо$−1$ раз$x+1$. Вибудовуйте подібні терміни. Міняйте знаки, додайте. Запишіть залишок у вигляді дробу з дільником як знаменником.	$.$
Щоб перевірити, помножте$(x+2)(x^3−2x^2+3x−1−4x+2)$. Результат повинен бути$x^4−x^2+5x−6$.

Спробуйте! $\PageIndex{9}$

Знайдіть частку:$(x^4−7x^2+7x+6)÷(x+3)$.

Відповідь: $x^3−3x^2+2x+1+3x+3$

Спробуйте! $\PageIndex{10}$

Знайдіть частку:$(x^4−11x^2−7x−6)÷(x+3)$.

Відповідь: $x^3−3x^2−2x−1−3x+3$

У наступному прикладі ми розділимо на$2a−3$. Коли ми ділимо, нам доведеться розглянути константи, а також змінні.

Приклад$\PageIndex{6}$

Знайдіть частку:$(8a^3+27)÷(2a+3)$.

Рішення

Цього разу ми покажемо поділ всього за один крок. Нам потрібно додати два заповнювачі для того, щоб розділити.

	$.$
	$.$

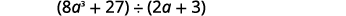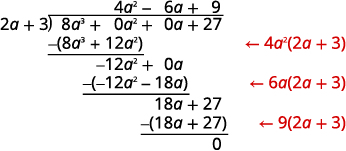Щоб перевірити, помножте$(2a+3)(4a^2−6a+9)$.

Результат повинен бути$8a^3+27$.

Спробуйте! $\PageIndex{11}$

Знайдіть частку:$(x^3−64)÷(x−4)$.

Відповідь: $x^2+4x+16$

Спробуйте! $\PageIndex{12}$

Знайдіть частку:$(125x^3−8)÷(5x−2)$.

Відповідь: $25x^2+10x+4$

Розділити поліноми за допомогою синтетичного поділу

Як ми вже згадували раніше, математики люблять знаходити закономірності, щоб полегшити свою роботу. Оскільки довгий поділ може бути нудним, давайте подивимося на довгий поділ, який ми зробили в прикладі, і шукаємо деякі закономірності. Ми будемо використовувати це як основу для того, що називається синтетичним поділом. Така ж проблема у форматі синтетичного поділу показана далі.

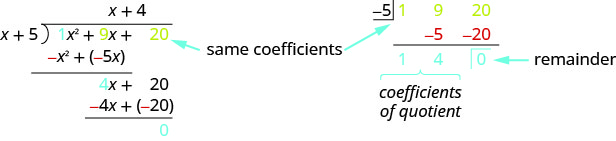
$На малюнку показано довге поділ 1 х в квадраті плюс 9 х плюс 20, розділене на х плюс 5 прямо поруч з тією ж проблемою, виконаною з синтетичним поділом. У задачі довгого ділення коефіцієнти дивідендів 1 і 9 і 20, а нуль дільника - від'ємний 5. У задачі синтетичного ділення просто запишемо числа від'ємні 5 1 9 20 з рядком, що розділяє негативне 5. У задачі довгого поділу віднімаються члени 5 х і 20. У задачі синтетичного ділення другий рядок - це числа від'ємні 5 та від'ємні 20. Залишок задачі дорівнює 0, а частка дорівнює x плюс 4. Синтетичне ділення ставить ці коефіцієнти як останній рядок 1 4 0.$

Синтетичний поділ в основному просто видаляє непотрібні повторювані змінні і числа. Тут все$x$ і$x^2$ видаляються. а також$−x^2$ і$−4x$ як вони протилежні терміну вище.

Перший ряд синтетичного поділу - коефіцієнти дивідендів. The$−5$ є протилежністю 5 в дільнику.
Другий ряд синтетичного поділу - це числа, показані червоним кольором в задачі про поділ.
Третій ряд синтетичного поділу - це числа, показані синім кольором в задачі ділення.

Зверніть увагу, що частка і залишок показані в третьому рядку.

\[\text{Synthetic division only works when the divisor is of the form }x−c. \nonumber \]

Наступний приклад пояснить процес.

Приклад$\PageIndex{7}$

Використовуйте синтетичне ділення, щоб знайти частку та залишок, коли$2x^3+3x^2+x+8$ ділиться на$x+2$.

Рішення

Напишіть дивіденди зі зменшенням повноважень$x$.	$.$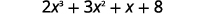
Запишіть коефіцієнти членів як перший ряд синтетичного поділу.	$.$
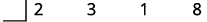Запишіть дільник як$x−c$ і помістіть c у синтетичному діленні в поле дільника.	$.$
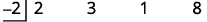Збити перший коефіцієнт до третього ряду.	$.$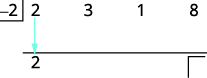
Помножте цей коефіцієнт на дільник і помістіть результат у другому рядку під другим коефіцієнтом.	$.$
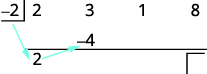Складіть другий стовпчик, помістивши результат в третій ряд.	$.$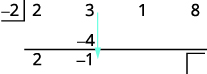
Помножте цей результат на дільник і помістіть результат у другому рядку під третім коефіцієнтом.	$.$
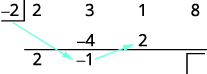Складіть третій стовпчик, помістивши результат в третій ряд.	$.$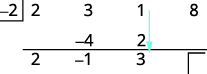
Помножте цей результат на дільник і помістіть результат у третьому рядку під третім коефіцієнтом.	$.$
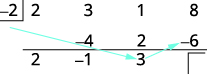Складіть кінцевий стовпчик, поклавши результат в третій ряд.	$.$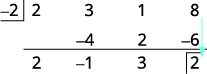
Частка є,$2x^2−1x+3$ а залишок дорівнює 2.

Поділ завершено. Цифри в третьому ряду дають нам результат. The$2\space\space\space−1\space\space\space3$ є коефіцієнти частки. Частка є$2x^2−1x+3$. 2 в коробці в третьому ряду - це залишок.

Перевірка:

$\begin{align} (\text{quotient})(\text{divisor}) + \text{remainder} &= \text{dividend} \nonumber\\ (2x^2−1x+3)(x+2)+2 &\overset{?}{=} 2x^3+3x^2+x+8 \nonumber\\ 2x^3−x^2+3x+4x^2−2x+6+2 &\overset{?}{=} 2x^3+3x^2+x+8 \nonumber\\ 2x^3+3x^2+x+8 &= 2x^3+3x^2+x+8\checkmark \nonumber \end{align} $

Спробуйте! $\PageIndex{13}$

Використовуйте синтетичне ділення, щоб знайти частку та залишок, коли$3x^3+10x^2+6x−2$ ділиться на$x+2$.

Відповідь: $3x^2+4x−2;\space 2$

Спробуйте! $\PageIndex{14}$

Використовуйте синтетичне ділення, щоб знайти частку та залишок, коли$4x^3+5x^2−5x+3$ ділиться на$x+2$.

Відповідь: $4x^2−3x+1; 1$

У наступному прикладі ми зробимо всі кроки разом.

Приклад$\PageIndex{8}$

Використовуйте синтетичне ділення, щоб знайти частку та залишок, коли$x^4−16x^2+3x+12$ ділиться на$x+4$.

Рішення

Поліном$x^4−16x^2+3x+12$ має свій термін у порядку зі спадним ступенем, але ми помічаємо, що$x^3$ терміна немає. Ми додамо 0 як заповнювач для цього$x^3$ терміну. За$x−c$ формою дільник є$x−(−4)$.

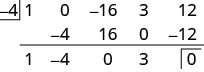
$На малюнку показані результати використання синтетичного ділення на прикладі многочлена х до четвертого степеня мінус 16 х в квадраті плюс 3 х плюс 12 ділиться на х плюс 4. Число дільника, якщо від'ємне 4. Перший ряд - 1 0 негативний 16 3 12. Перший стовпець - 1 порожній 1. Другий стовпець від'ємний 16 16 0. Третій стовпець - 3 0 3. Четвертий стовпець 12 негативний 12 0.$

Ми розділили$4^{\text{th}}$ градусний многочлен на$1^{\text{st}}$ градусний многочлен, тому частка буде поліном$3^{\text{rd}}$ ступеня.

Читаючи з третього ряду, частка має коефіцієнти$1\space\space\space−4\space\space\space0\space\space\space3$, що є$x^3−4x^2+3$. Залишок
дорівнює 0.

Спробуйте! $\PageIndex{15}$

Використовуйте синтетичне ділення, щоб знайти частку та залишок, коли$x^4−16x^2+5x+20$ ділиться на$x+4$.

Відповідь: $x^3−4x^2+5;\space 0$

Спробуйте! $\PageIndex{16}$

Використовуйте синтетичне ділення, щоб знайти частку та залишок, коли$x^4−9x^2+2x+6$ ділиться на$x+3$.

Відповідь: $x^3−3x^2+2;\space 0$

Розділити поліноміальні функції

Подібно до того, як поліноми можна розділити, поліноміальні функції також можна розділити.

Означення: ПОДІЛ ПОЛІНОМІАЛЬНИХ ФУНКЦІЙ

Для функцій$f(x)$ і$g(x)$, де$g(x)\neq 0$,

\[\left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)} \nonumber\]

Приклад$\PageIndex{9}$

Для функцій$f(x)=x^2−5x−14$ і$g(x)=x+2$, знайдіть:

$\left(\dfrac{f}{g}\right)(x)$
$\left(\dfrac{f}{g}\right)(−4)$.

Рішення

ⓐ

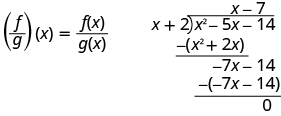
$Рівняння показує f над g x дорівнює f x, розділеному на g x. Це перекладається на задачу ділення, яка показує x у квадраті мінус 5x мінус 14, поділений на x плюс 2. Коефіцієнт дорівнює x мінус 7.$

$\begin{array} {ll} {\text{Substitute for }f(x)\text{ and }g(x).} &{\left(\dfrac{f}{g}\right)(x)=\dfrac{x^2−5x−14}{x+2}} \\[5pt] {\text{Divide the polynomials.}} &{\left(\dfrac{f}{g}\right)(x)=x−7} \end{array} $

ⓑ Частково ⓐ ми знайшли$\left(\dfrac{f}{g}\right)(x)$ і тепер просять знайти$\left(\dfrac{f}{g}\right)(−4)$.

$\begin{array} {ll} {} &{\left(\dfrac{f}{g}\right)(x)=x−7} \\[5pt] {\text{To find }\left(\dfrac{f}{g}\right)(−4), \text{ substitute }x=−4.} &{\left(\dfrac{f}{g}\right)(−4)=−4−7} \\[5pt] {} &{\left(\dfrac{f}{g}\right)(−4)=−11} \end{array}$

Спробуйте! $\PageIndex{17}$

Для функцій$f(x)=x^2−5x−24$ і$g(x)=x+3$, знайдіть:

$\left(\dfrac{f}{g}\right)(x)$
$\left(\dfrac{f}{g}\right)(−3)$.

Відповідь на: $\left(\dfrac{f}{g}\right)(x)=x−8$
Відповідь б: $\left(\dfrac{f}{g}\right)(−3)=−11$

Спробуйте! $\PageIndex{18}$

Для функцій$f(x)=x2−5x−36$ і$g(x)=x+4$, знайдіть:

$\left(\dfrac{f}{g}\right)(x)$
$\left(\dfrac{f}{g}\right)(−5)$.

Відповідь на: $\left(\dfrac{f}{g}\right)(x)=x−9$
Відповідь б: $\left(\dfrac{f}{g}\right)(x)=x−9$

Використовуйте теорему про залишок і коефіцієнт

Давайте подивимося на проблеми поділу, які ми щойно працювали, які закінчилися залишком. Вони узагальнені на графіку нижче. Якщо взяти дивіденд від кожної задачі поділу і використовувати його для визначення функції, ми отримаємо функції, показані на діаграмі. Коли дільник записується як$x−c$, значення функції at$c$,$f(c)$, збігається з залишком від задачі ділення.

Дивіденди	дільник$x−c$	Залишок	Функція	$f(c)$
$x^4−x^2+5x−6$	\ (x−c\)» перевірка даних="верх">$x−(−2)$	$−4$	$f(x)=x^4−x^2+5x−6$	\ (f (c)\)» перевірка даних = «верх">$−4$
$3x^3−2x^2−10x+8$	\ (x−c\)» перевірка даних="верх">$x−2$	4	$f(x)=3x^3−2x^2−10x+8$	\ (f (c)\)» перевірка даних = «верх">4
$x^4−16x^2+3x+15$	\ (x−c\)» перевірка даних="верх">$x−(−4)$	3	$f(x)=x^4−16x^2+3x+15$	\ (f (c)\)» перевірка даних = «верх">3

Щоб побачити це більш загалом, ми розуміємо, що ми можемо перевірити проблему ділення, множивши частку на дільник і додати залишок. У позначенні функції ми могли б сказати, щоб отримати дивіденд$f(x)$, ми множимо частку,$q(x)$ раз дільник$x−c$, і додати залишок,$r$.

	$.$
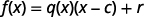Якщо ми оцінюємо це на$c$, то отримаємо:	$.$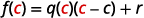
	$.$
	$.$

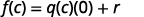Це призводить нас до теореми про залишок.

Визначення: ТЕОРЕМА ЗАЛИШКУ

Якщо поліноміальна функція$f(x)$ ділиться на$x−c$, то залишок дорівнює$f(c)$.

Приклад$\PageIndex{10}$

Використовуйте теорему про залишок, щоб знайти залишок при$f(x)=x^3+3x+19$ діленні на$x+2$.

Рішення

Щоб використовувати теорему про залишок, ми повинні використовувати дільник у$x−c$ вигляді. Ми можемо записати дільник$x+2$ як$x−(−2)$. Отже, наше$c$ є$−2$.

Щоб знайти залишок, оцінюємо,$f(c)$ який є$f(−2)$.

	$.$
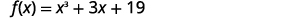Щоб оцінити$f(−2)$, підставити$x=−2$.	$.$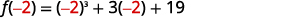
Спростити.	$.$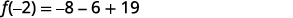
	$.$
	Залишок дорівнює 5 при$f(x)=x^3+3x+19$ діленні на$x+2$.
Перевірка: Використовуйте синтетичне поділ для перевірки.
$.$
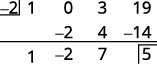Залишок - 5.

Спробуйте! $\PageIndex{19}$

Використовуйте теорему про залишок, щоб знайти залишок при$f(x)=x^3+4x+15$ діленні на$x+2$.

Відповідь: $−1$

Спробуйте! $\PageIndex{20}$

Використовуйте теорему про залишок, щоб знайти залишок при$f(x)=x^3−7x+12$ діленні на$x+3$.

Відповідь: $6$

Коли ми розділили$8a^3+27$ на$2a+3$ в прикладі результат був$4a^2−6a+9$. Щоб перевірити нашу роботу, множимо$4a2−6a+9$ на,$2a+3$ щоб отримати$8a^3+27$.

\[(4a^2−6a+9)(2a+3)=8a^3+27 \nonumber \]

Написано таким чином, ми можемо бачити, що$4a^2−6a+9$ і$2a+3$ є факторами$8a^3+27$. Коли ми робили поділ, залишок дорівнював нулю.

Всякий раз$x−c$, коли дільник, ділить поліноміальну функцію$f(x)$, і в результаті залишок від нуля, ми говоримо, що$x−c$ це множник$f(x)$.

Зворотне теж вірно. Якщо$x−c$ є множником,$f(x)$ то$x−c$ буде ділити поліноміальну функцію, в результаті чого залишок дорівнює нулю.

Про це ми розповімо в Теоремі Фактора.

Визначення: ТЕОРЕМА ФАКТОРА

Для будь-якої поліноміальної функції$f(x)$

якщо$x−c$ є фактором$f(x)$, то$f(c)=0$
якщо$f(c)=0$,$x−c$ то є фактором$f(x)$

Приклад$\PageIndex{11}$

Використовуйте теорему про залишок, щоб визначити, чи$x−4$ є множником$f(x)=x^3−64$.

Рішення

Теорема фактора говорить нам, що$x−4$ це коефіцієнт$f(x)=x^3−64$ if$f(4)=0$.

$\begin{array} {ll} {} &{f(x)=x^3−64} \\[5pt] {\text{To evaluate }f(4) \text{ substitute } x=4.} &{f(4)=4^3−64} \\[5pt] {\text{Simplify.}} &{f(4)=64−64} \\[5pt]{\text{Subtract.}} &{f(4)=0} \end{array}$

Так як$f(4)=0, x−4$ є фактором$f(x)=x^3−64$.

Спробуйте! $\PageIndex{21}$

Використовуйте теорему фактора, щоб визначити$x−5$, чи є множником$f(x)=x^3−125$.

Відповідь: так

Спробуйте! $\PageIndex{22}$

Використовуйте теорему фактора, щоб визначити$x−6$, чи є множником$f(x)=x^3−216$.

Відповідь: так

Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з ділильними поліномами.

Ділення многочлена на біноміал
Теорема про синтетичне поділ та залишок

Ключові поняття

Розподіл многочлена на мономіал
- Щоб розділити многочлен на мономіал, розділіть кожен член многочлена на моном.
Розподіл поліноміальних функцій
- Для функцій$f(x)$ і$g(x)$, де$g(x)\neq 0$,
  $\left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)}$
Теорема про залишок
- Якщо поліноміальна функція$f(x)$ ділиться на$x−c$, то залишок дорівнює$f(c)$.
Теорема про множник: Для будь-якої поліноміальної функції$f(x)$
- якщо$x−c$ є фактором$f(x)$, то$f(c)=0$
- якщо$f(c)=0$,$x−c$ то є фактором$f(x)$

\(\require{enclose}\)	\(\qquad (x^2+9x+20) \div (x+5)\)
Напишіть це як довгу проблему поділу. Переконайтеся, що дивіденди в стандартній формі.	\(\qquad x+5\enclose{longdiv}{ x^2+9x+20\phantom{0}} \)
Розділити\(x^2\) на\(x\). Це може допомогти запитати себе: «На що мені потрібно \(x\) помножити, щоб отримати\(x^2\)?»	\(\qquad \begin{array}{r} {\color{red}x}\hspace{2.3em}\\[-3pt] {\color{red}x}+5\enclose{longdiv}{ {\color{red}x^2}+9x+20\phantom{0}} \end{array}\)
Поставте відповідь\(x\), в частку над\(x\) терміном. Множимо\(x\) раз\(x+5\). Вибудовуйте подібні умови під дивідендами.	\(\qquad \begin{array}{r}x\hspace{2.3em}\\[-3pt] x+5\enclose{longdiv}{x^2+9x+20\phantom{0}}\\[-3pt] \underline{\color{red}x^2+5x}\hspace{2.4em} \end{array}\)
Відняти\(x^2+5x\) від\(x^2+9x\). Можливо, вам буде легше змінити знаки, а потім додати. Потім збити останній термін,\(20.\)	\(\qquad \begin{array}{r}x\hspace{2.3em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] {\color{red}4x+20}\hspace{0.5em} \end{array}\)
Розділити\(4x\) на\(x\). Це може допомогти запитати себе: «На що мені потрібно\(x\) помножити, щоб отримати\(4x\)?» Поставте відповідь\(4\), в частку над постійним терміном.	\(\qquad \begin{array}{r}x+\phantom{0}{\color{red}4}\hspace{.5em}\\[-3pt] {\color{red}x}+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] {\color{red}4x}+20\hspace{0.5em} \end{array}\)
Помножте 4 рази\(x+5\).	\(\qquad \begin{array}{r}x+\phantom{0}4\hspace{.5em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] 4x+20\hspace{0.5em}\\[-3pt] \underline{ \color{red}4x+20}\hspace{.5em} \end{array}\)
Відняти\(4x+20\) від\(4x+20\).	\(\qquad \begin{array}{r}x+\phantom{0}4\hspace{.5em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] 4x+20\hspace{.5em}\\[-3pt] \underline{{\color{red}-}4x+({\color{red}-}20)}\\[-3pt] 0\hspace{.33em}\end{array}\)
Перевірка: \(\begin{array} {ll} {\text{Multiply the quotient by the divisor.}} &{(x+4)(x+5)} \\ {\text{You should get the dividend.}} &{x^2+9x+20\checkmark}\\ \end{array}\)

Дивіденди	дільник\(x−c\)	Залишок	Функція	\(f(c)\)
\(x^4−x^2+5x−6\)	\ (x−c\)» перевірка даних="верх">\(x−(−2)\)	\(−4\)	\(f(x)=x^4−x^2+5x−6\)	\ (f (c)\)» перевірка даних = «верх">\(−4\)
\(3x^3−2x^2−10x+8\)	\ (x−c\)» перевірка даних="верх">\(x−2\)	4	\(f(x)=3x^3−2x^2−10x+8\)	\ (f (c)\)» перевірка даних = «верх">4
\(x^4−16x^2+3x+15\)	\ (x−c\)» перевірка даних="верх">\(x−(−4)\)	3	\(f(x)=x^4−16x^2+3x+15\)	\ (f (c)\)» перевірка даних = «верх">3

Приклад\(\PageIndex{1}\)

Спробуйте! \(\PageIndex{1}\)

Спробуйте! \(\PageIndex{2}\)

Приклад\(\PageIndex{2}\)

Спробуйте! \(\PageIndex{3}\)

Спробуйте! \(\PageIndex{4}\)

Означення: ДІЛЕННЯ ПОЛІНОМА НА МОНОМІАЛ

Приклад\(\PageIndex{3}\)

Спробуйте! \(\PageIndex{5}\)

Спробуйте! \(\PageIndex{6}\)

Приклад\(\PageIndex{4}\)

Спробуйте! \(\PageIndex{7}\)

Спробуйте! \(\PageIndex{8}\)

Приклад\(\PageIndex{5}\)

Спробуйте! \(\PageIndex{9}\)

Спробуйте! \(\PageIndex{10}\)

Приклад\(\PageIndex{6}\)

Спробуйте! \(\PageIndex{11}\)

Спробуйте! \(\PageIndex{12}\)

Приклад\(\PageIndex{7}\)

Спробуйте! \(\PageIndex{13}\)

Спробуйте! \(\PageIndex{14}\)

Приклад\(\PageIndex{8}\)

Спробуйте! \(\PageIndex{15}\)

Спробуйте! \(\PageIndex{16}\)

Означення: ПОДІЛ ПОЛІНОМІАЛЬНИХ ФУНКЦІЙ

Приклад\(\PageIndex{9}\)

Спробуйте! \(\PageIndex{17}\)

Спробуйте! \(\PageIndex{18}\)

Визначення: ТЕОРЕМА ЗАЛИШКУ

Приклад\(\PageIndex{10}\)

Спробуйте! \(\PageIndex{19}\)

Спробуйте! \(\PageIndex{20}\)

Визначення: ТЕОРЕМА ФАКТОРА

Приклад\(\PageIndex{11}\)

Спробуйте! \(\PageIndex{21}\)

Спробуйте! \(\PageIndex{22}\)

	$.$
Напишіть це як довгу проблему поділу. Переконайтеся, що дивіденди в стандартній формі з заповнювачами для відсутніх термінів.	$.$
Розділити\(x^4\) на\(x\). Поставте відповідь\(x^3\), в частку над\(x^3\) терміном. Множимо\(x^3\) раз\(x+2\). Вибудовуйте подібні терміни. Відніміть, а потім збийте наступний термін.	$.$
Розділити\(−2x^3\) на\(x\). Поставте відповідь\(−2x^2\), в частку над\(x^2\) терміном. Множимо\(−2x^2\) раз\(x+1\). Вибудовуйте подібні терміни Відніміть і збийте наступний термін.	$.$
Розділити\(3x^2\) на\(x\). Поставте відповідь\(3x\), в частку над\(x\) терміном. Множимо\(3x\) раз\(x+1\). Вибудовуйте подібні терміни. Відніміть і збийте наступний термін.	$.$
Розділити\(−x\) на\(x\). Поставте відповідь\(−1\), в частку над постійним терміном. Множимо\(−1\) раз\(x+1\). Вибудовуйте подібні терміни. Міняйте знаки, додайте. Запишіть залишок у вигляді дробу з дільником як знаменником.	$.$
Щоб перевірити, помножте\((x+2)(x^3−2x^2+3x−1−4x+2)\). Результат повинен бути\(x^4−x^2+5x−6\).

Напишіть дивіденди зі зменшенням повноважень\(x\).	$.$
Запишіть коефіцієнти членів як перший ряд синтетичного поділу.	$.$
Запишіть дільник як\(x−c\) і помістіть c у синтетичному діленні в поле дільника.	$.$
Збити перший коефіцієнт до третього ряду.	$.$
Помножте цей коефіцієнт на дільник і помістіть результат у другому рядку під другим коефіцієнтом.	$.$
Складіть другий стовпчик, помістивши результат в третій ряд.	$.$
Помножте цей результат на дільник і помістіть результат у другому рядку під третім коефіцієнтом.	$.$
Складіть третій стовпчик, помістивши результат в третій ряд.	$.$
Помножте цей результат на дільник і помістіть результат у третьому рядку під третім коефіцієнтом.	$.$
Складіть кінцевий стовпчик, поклавши результат в третій ряд.	$.$
Частка є,\(2x^2−1x+3\) а залишок дорівнює 2.

	$.$
Якщо ми оцінюємо це на\(c\), то отримаємо:	$.$
	$.$
	$.$

	$.$
Щоб оцінити\(f(−2)\), підставити\(x=−2\).	$.$
Спростити.	$.$
	$.$
	Залишок дорівнює 5 при\(f(x)=x^3+3x+19\) діленні на\(x+2\).
Перевірка: Використовуйте синтетичне поділ для перевірки.
$.$
Залишок - 5.