5.5: Ділильні многочлени

Цілі навчання

• Використовуйте довге ділення для поділу многочленів.
• Використовуйте синтетичне ділення для поділу поліномів.

Зовнішній вигляд Меморіалу Лінкольна у Вашингтоні, округ Колумбія, являє собою велику прямокутну тверду$61.5$ речовину довжиною метрів (м), шириною$40$ м та висотою$30$ м.$^1$

Ми легко можемо знайти обсяг, використовуючи елементарну геометрію.

$$\begin{align*} V&=l \; {\cdot} \; w \; {\cdot} \; h \\ &=61.5 \; {\cdot} \; 40 \; {\cdot} \; 30 \\ &=73,800 \end{align*}$$

Так обсяг дорівнює$73,800$ кубічним метрам ($m^3$).

Ілюстрація$\PageIndex{1}$: Меморіал Лінкольна, Вашингтон, округ Колумбія (кредит: Рон Когсуелл, Flickr)

Припустимо, ми знали обсяг, довжину і ширину. Ми могли б розділити, щоб знайти висоту.

$$\begin{align*} h&=\dfrac{V}{l{\cdot}w} \\&=\dfrac{73,800}{61.5{\cdot}40} \\ &=30 \end{align*}$$

Як ми можемо підтвердити з розмірів вище, висота 30 м Ми можемо використовувати аналогічні методи, щоб знайти будь-який з відсутніх розмірів. Ми також можемо використовувати той самий метод, якщо будь-яке або всі вимірювання містять змінні вирази. Наприклад, припустимо, що обсяг прямокутного твердого тіла задається многочленом$3x^4−3x^3−33x^2+54x$. Довжина твердого тіла задається по$3x$; ширина задається по$x−2$.

Щоб знайти висоту твердого тіла, ми можемо використовувати поліноміальне ділення, яке є фокусом цього розділу.

Використання довгого ділення для поділу многочленів

Ми знайомі з алгоритмом поділу довгих для звичайної арифметики. Починаємо з поділу на цифри дивідендів, які мають найбільше місце значення. Ділимо, множимо, віднімаємо, включаємо цифру в наступне місце значення позиції, і повторюємо. Наприклад, давайте розділимо 178 на 3, використовуючи довге ділення.

Ще один спосіб подивитися на рішення - це сума частин. Це повинно виглядати звично, оскільки це той самий метод, який використовується для перевірки ділення в елементарній арифметиці.

$$\begin{align*} \text{dividend}&=(\text{divisor}{\cdot}\text{quotient})+\text{remainder} \\ 178&=(3{\cdot}59)+1 \\ &=177+1 \\ &=178\end{align*}$$

Ми називаємо це алгоритмом поділу і обговоримо його більш формально, подивившись на приклад.

Поділ многочленів, що містять більше одного члена, має подібність до довгого ділення цілих чисел. Ми можемо записати поліноміальний дивіденд як добуток дільника, а частка додається до залишку. Умови поліноміального поділу відповідають цифри (і значення місця) цілого числового ділення. Цей метод дозволяє розділити два многочлена. Наприклад, якби ми ділили за$2x^3−3x^2+4x+5$$x+2$ допомогою алгоритму довгого ділення, це виглядало б так:

\ [\ require {enclose}\ begin {масив} {rll}\ великий x+2\ inclose {longdiv} {2x^3-3x^2+4x+5\ фантом {0}} &
\ qquad &\ large2x^3\ текст {розділений на} х\ текст {є} 2x^2.\\ [-3pt]
\ великий x+2\ inclose { longdiv} {2x^3-3x^2+4x+5\ фантом {0}} &\ qquad &\\
\ [8pt]\ великий 2x^2\ hпробіл {5.45em} &\ qquad\\ [-3pt]
\ великий x+2\ вкласти {2x^3-3x^2+4x+5\ фантом {0}} &\ qquad\\ [[-3pt]
\ великий\ підкреслення {-\ ліворуч (2x^3 + 4x^2\ праворуч)}\ hspace {4.9em} & \ qquad &\ великий\ текст {Множення} x+2\ текст {на} 2x^2\ текст {і відніміть.}\\ [-3pt]
\ великий -7x^2+4x\ hspace {2.8em} &\ qquad &\ великий\ текст {Збити наступний термін.}\\ [8pt]

\ великий 2x^2 - 7x\ hspace {2.85em}\ qquad &\ великий -7x^2\ текст {розділений на} x\ текст {is} -7x.\\ [-3pt]
\ великий x+2\ вкласти {longdiv} {2x^3-3x^2+4x+5\ фантом {0}} &\ qquad\\ [-3pt]
\ великий\ підкреслення {-\ ліворуч (2x^3 + 4x^2\ праворуч)}\ hspace {4.9em} &\ qquad\\\ [-3* pt]
\ великий -7x^2+4x\ hspace {2.8em} &\ qquad &\\ [-3pt]
\ великий\ підкреслення {-\ ліворуч (-7x^2 - 14x\ праворуч)}\ hspace {2.0em} &\ qquad &\ великий\ текст {Множення} x+2\ текст {на} -7x.\\ [-3pt]
\ великий 18x+5\ фантом {0} &\ qquad &\ великий\ текст {Відніміть і збити наступний термін.}\ [8pt]

\ великий 2x^2 - 7х+18 &\ qquad &\ великий 18x\ текст {розділений на} х\ текст {є} 18.\\ [-3pt]
\ великий x+2\ вкласти {longdiv} {2x^3-3x^2+4x+5\ фантом {0}} &\ qquad &\\ [-3pt]
\ великий\ підкреслення {-\ лівий (2x^3+ 4x^2\ праворуч)}\ hspace 4.9em} &\ qquad &\\ [-3pt]
\ великий -7x^2+4x\ hspace {2.8 em} &\ qquad &\\ [-3pt]
\ великий\ підкреслення {-\ лівий (-7x^2 - 14x\ праворуч)}\ hspace {2.0em} &\ qquad &\\ [-3pt]
\ великий 18x+\ фантом {0} 5 &\ qquad &\\ [-3pt]
\ великий\ підкреслення {-\ лівий (18x + 36\ право)}\ hspace {-0.45em} &\ qquad &\ великий\ текст {Множення} x+2\ текст {на} 18.\\ [-3pt]
\ великий -31 &\ qquad &\ великий\ текст {Відняти.}\\ [8pt]
\ end {масив}\ nonumber\]

Ми знайшли

$$\dfrac{2x^3−3x^2+4x+5}{x+2}=2x^2−7x+18−\dfrac{31}{x+2} \nonumber$$

або

$$2x^3−3x^2+4x+5=(x+2)(2x^2−7x+18)−31 \nonumber$$

Ми можемо визначити дивіденд, дільник, частку та залишок.

Написання результату таким чином ілюструє алгоритм поділу.

Алгоритм поділу

Алгоритм поділу стверджує, що, враховуючи поліноміальний дивіденд$f(x)$ і ненульовий поліноміальний дільник,$d(x)$ де ступінь менше або дорівнює ступеня$f(x)$, існують унікальні поліноми$q(x)$ і$r(x)$ такі, що$d(x)$

$$f(x)=d(x)q(x)+r(x)$$

$q(x)$є часткою і$r(x)$ є залишком. Залишок або дорівнює нулю, або має ступінь строго менше$d(x)$.

Якщо$r(x)=0$, то$d(x)$ поділяє рівномірно на$f(x)$. Це означає, що в даному випадку обидва$d(x)$ і$q(x)$ є факторами$f(x)$.

Задано многочлен та біном, використовуйте довге ділення, щоб розділити многочлен на біном

1. Налаштуйте проблему поділу.
2. Визначте перший член частки шляхом ділення провідного члена дивіденду на провідний член дільника.
3. Помножте відповідь на дільник і запишіть його нижче аналогічних термінів дивіденду.
4. Відніміть нижній біном від верхнього біном.
5. Збити наступний термін дивідендів.
6. Повторюйте кроки 2—5 до досягнення останнього терміну дивідендів.
7. Якщо залишок ненульовий, виражаємо як дріб, використовуючи дільник як знаменник.

Приклад$\PageIndex{1}$: Using Long Division to Divide a Second-Degree Polynomial

Розділити$5x^2+3x−2$ на$x+1$.

Рішення

Коефіцієнт є$5x−2$. Залишок дорівнює 0. Пишемо результат як

$$\dfrac{5x^2+3x−2}{x+1}=5x−2 \nonumber$$

або

$$5x^2+3x−2=(x+1)(5x−2) \nonumber$$

Аналіз

Ця задача поділу мала залишок 0. Це говорить нам про те, що дивіденд ділиться рівномірно на дільник, і що дільник є коефіцієнтом дивідендів.

Приклад$\PageIndex{2}$: Using Long Division to Divide a Third-Degree Polynomial

Розділити$6x^3+11x^2−31x+15$ на$3x−2$.

Рішення

\ [\ вимагають {вкласти}\ почати {масив} {rll}
\ великий 2x^2 +\ фантом {0} 5x-\ фантом {0} 7 &\ qquad &\ великий 6x^3\ текст {розділений на} 3x\ текст {є} 2x^2.\\ [-3pt]
\ великий 3x-2\ вкласти {longdiv} {6x^3+x2 ^2-31x+15} &\ qquad &\\ [-3pt]
\ великий\ підкреслення {-\ лівий (6x^3 - 4x^2 \ право)}\ hspace {5.8em} &\ qquad &\ великий\ текст {Множення} 3x-2\ текст {на} 2x^2.\\ [-3pt]
\ великий 15x^2-31x\ hspace {3.0em} &\ qquad &\ великий\ текст {Відніміть. Збити наступний член.} 15x^2\ текст {розділений на} 3x\ text {є} 5x.\\ [-3pt]
\ великий\ підкреслення {-\ лівий (15x^2 - 10x\ праворуч)}\ hspace {2.5em} &\ qquad &\ великий\ текст {множити} 3x-2\ текст {на} 5x.\\ [-3pt]
\ великий 21x+15\ hspace {0.5em} &\ qquad &\ великий\ текст {Відняти. Збити наступний член.} -21x\ текст {розділений на} 3x\ text {є} -7.\\ [-3pt]
\ великий\ підкреслення {-\ ліворуч (-21x + 14\ праворуч)}\ hspace {0.1em} &\ qquad &\ великий\ текст {множити} 3x-2\ текст {на} -7.\\ [-3pt]
\ великий 1\ hx пробіл {0.5em} &\ qquad &\ великий\ текст {Відняти. Залишок дорівнює 1.}\\ [8pt]
\ end {масив}\ nonumber\]

Є залишок 1. Ми можемо висловити результат у вигляді:

$$\dfrac{6x^3+11x^2−31x+15}{3x−2}=2x^2+5x−7+\dfrac{1}{3x−2} \nonumber$$

Аналіз

Ми можемо перевірити нашу роботу за допомогою алгоритму поділу, щоб переписати рішення. Потім розмножуємо.

$$(3x−2)(2x^2+5x−7)+1=6x^3+11x^2−31x+15 \nonumber$$

Зверніть увагу, як ми пишемо наш результат,

• дивіденд$6x^3+11x^2−31x+15$
• дільник$3x−2$
• частка$2x^2+5x−7$
• залишок -$1$

Спробуйте! $\PageIndex{2}$

Розділити$16x^3−12x^2+20x−3$ на$4x+5$.

Рішення

$4x^2−8x+15−\dfrac{78}{4x+5}$

Використання синтетичного ділення для поділу поліномів

Як ми бачили, довгий поділ многочленів може включати багато кроків і бути досить громіздким. Синтетичне ділення - це стенографічний метод ділення многочленів для окремого випадку ділення на лінійний коефіцієнт, провідний коефіцієнт якого дорівнює$1.$

Для ілюстрації процесу нагадаємо приклад на початку розділу.

Розділіть$2x^3−3x^2+4x+5$ за$x+2$ допомогою алгоритму поділу довгих.

Остаточна форма процесу виглядала так:

\ [\ вимагають {вкласти}\ почати {масив} {rl}\ великий 2x^2 - 7x+18 &\\ [-3pt]
\ великий x+2\\ вкласти {longdiv} {2x^3-3x^2+4x+5\ фантом {0}} &\\ [-3pt]
\ великий\ підкреслення {-\ ліворуч (2x^3 + 4x^2\ праворуч)\\ h пробіл {4.9em} &\\ [-3pt]
\ великий -7x^2+4x\ hspace {2.8em} &\\\ [-3pt]
\ великий\ підкреслення {-\ ліворуч (-7x^2 - 14x\ праворуч)}\ hspace {2.0em} &\\ [-3pt]
\ великий 18x+\ фантом {0} 5 &\\ [-3pt]
\ великий\ підкреслення {-\ ліворуч (18x + 36\ праворуч)}\ hspace {-0.45em} &\\ [-3pt]
\ великий -31 &\\ [8pt]
\ кінець {масив}\ nonumber \]

У таблиці багато повторень. Якщо ми не запишемо змінні, а замість цього вибудовуємо їх коефіцієнти в стовпці під знаком ділення, а також усуваємо часткові добутки, у нас вже є простіша версія всієї проблеми.

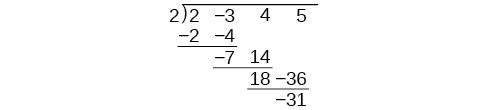
Синтетичне поділ несе таке спрощення ще на кілька кроків. Згорніть таблицю, перемістивши кожен з рядків вгору, щоб заповнити всі вільні місця. Також замість ділення на 2, як ми б при діленні цілих чисел, потім множимо і віднімаємо середній твір, змінюємо знак «дільника» на —2, множимо і складаємо. Процес починається зі збивання провідного коефіцієнта.

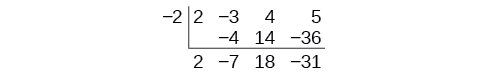
Потім множимо його на «дільник» і додаємо, повторюючи цей процес стовпець за стовпцем, поки не залишиться ніяких записів. Нижній рядок представляє коефіцієнти частки; останній запис нижнього ряду - залишок. У цьому випадку частка є,$2x^2–7x+18$ а решта -$–31.$ Процес буде зрозумілішим у прикладі$\PageIndex{3}$.

Синтетичний поділ

Синтетичне ділення - це ярлик, який може бути використаний, коли дільник є біноміальним за формою$x−k$. При синтетичному поділі в процесі ділення використовуються тільки коефіцієнти.

За даними двох поліномів використовуйте синтетичне ділення для поділу

1. Запишіть$k$ для дільника.
2. Напишіть коефіцієнти дивідендів.
3. Знизити коефіцієнт свинцю.
4. Помножте коефіцієнт відведення на$k$. Запишіть товар в наступну графу.
5. Додайте терміни другого стовпця.
6. Помножте результат на$k$. Запишіть товар в наступну графу.
7. Повторіть кроки 5 і 6 для інших стовпчиків.
8. Використовуйте нижні цифри, щоб написати частку. Число в останньому стовпці є залишком і має ступінь 0, наступне число праворуч має ступінь 1, наступне число праворуч має ступінь 2, і так далі.

Приклад$\PageIndex{3}$: Using Synthetic Division to Divide a Second-Degree Polynomial

Використовуйте синтетичне поділ, щоб розділити$5x^2−3x−36$ на$x−3$.

Рішення

Почніть з налаштування синтетичного поділу. Напишіть$k$ і коефіцієнти.

Збити коефіцієнт свинцю. Помножте коефіцієнт відведення на$k$.

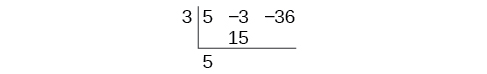
Продовжуйте, додаючи цифри у другому стовпці. Помножте отримане число$k$ на.Запишіть результат в наступний стовпець. Потім складіть цифри в третьому стовпці.

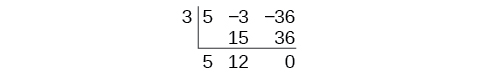
Результат є$5x+12$. Залишок дорівнює 0. Так$x−3$ і коефіцієнт початкового многочлена.

Аналіз

Так само, як і при довгому діленні, ми можемо перевірити нашу роботу, помноживши частку на дільник і додаючи залишок.

$$(x−3)(5x+12)+0=5x^2−3x−36 \nonumber$$

Приклад$\PageIndex{4}$: Using Synthetic Division to Divide a Third-Degree Polynomial

Використовуйте синтетичне поділ, щоб розділити$4x^3+10x^2−6x−20$ на$x+2$.

Рішення

Біноміальний дільник$x+2$ так$k=−2$. Додайте кожен стовпець, помножте результат на —2 і повторюйте, поки не буде досягнутий останній стовпець.

\ [\ large {\ begin {масив} {c} -2\\\\\\ кінець {масив}} {
\ begin
{align*} &\\ [0pt]
& {\ begin {масив} {r|}\\ [0pt]\ [0pt]\ end {масив}
\\ [1pt] &\\ end {align*}}\\ [1pt]
&\\ end {align*}}\ [1pt] &\\ end {align*}\! \!
{\ begin {масив} {rrrr}
1 & -1 & -11
& 18\\ & 2 & -18\\
\ hline 1 & 1 & -9 & 0
\ кінець {масив}}
\ nonumber\]

Результат є$4x^2+2x−10$.

Залишок дорівнює 0. Таким чином,$x+2$ є фактором$4x^3+10x^2−6x−20$.

Аналіз

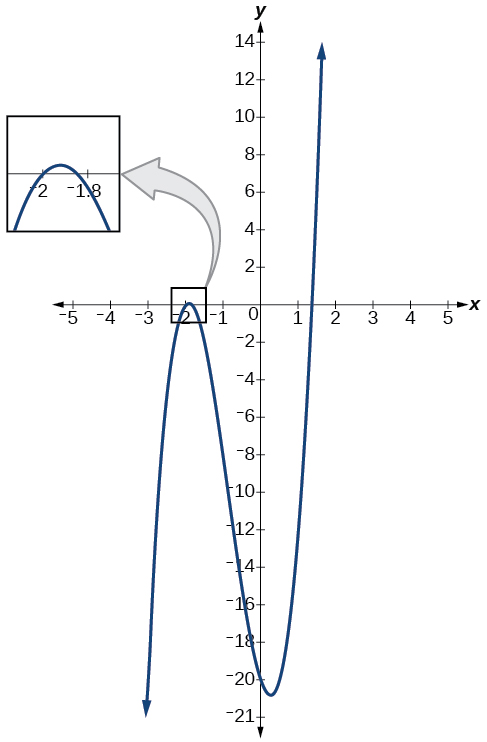
Графік функції полінома на$f(x)=4x^3+10x^2−6x−20$ малюнку$\PageIndex{2}$ показує нуль ат$x=k=−2$. Це підтверджує, що$x+2$ є фактором$4x^3+10x^2−6x−20$.

Малюнок$\PageIndex{2}$

Приклад$\PageIndex{5}$: Using Synthetic Division to Divide a Fourth-Degree Polynomial

Використовуйте синтетичне поділ, щоб розділити$−9x^4+10x^3+7x^2−6$ на$x−1$.

Рішення

Зверніть увагу, що немає$x$ -термін. Ми будемо використовувати нуль як коефіцієнт для цього терміну.

\ [\ large {\ begin {масив} {c} 1\\\\\ кінець {масив}} {
\ почати {вирівнювати*}
&\\ [0pt] & {\ begin {масив} {r|}\\ [0pt]
\ [0pt]\ [0pt]\ end {масив}
\\ [1pt] &\\ end {align*}}\\ [1pt]
&\\ end {align*}}\ [1pt] &\\ end {align*}\! \!
{\ begin {масив} {rrrrr}
-9 & 10 & 7 & 0 &-6\\
& -9 & 1 & 8\\\ hline -9\
\\ рядок -9 & 1 & 1 & 1 & 1 & 8 & 2
\ кінець {масив}}
\ nonumber\]

Результат є$−9x^3+x^2+8x+8+\dfrac{2}{x−1}$.

Спробуйте! $\PageIndex{3}$

Використовуйте синтетичне поділ, щоб розділити$3x^4+18x^3−3x+40$ на$x+7$.

Рішення

$3x^3−3x^2+21x−150+\dfrac{1090}{x+7}$

Використання поліноміального поділу для розв'язання прикладних задач

Поліноміальне ділення може бути використано для вирішення різноманітних прикладних задач, що включають вирази для площі та обсягу. Ми розглянули додаток на початку цього розділу. Тепер ми вирішимо цю проблему в наступному прикладі.

Приклад$\PageIndex{6}$: Using Polynomial Division in an Application Problem

Обсяг прямокутного твердого тіла задається многочленом$3x^4−3x^3−33x^2+54x$. Довжина твердого тіла задається,$3x$ а ширина задається$x−2$. Знайдіть висоту$h$ твердого тіла.

Рішення

Є кілька способів підходу до цієї проблеми. Нам потрібно розділити вираз для обсягу твердого тіла на вирази для довжини і ширини. Створимо ескіз, як на малюнку$\PageIndex{3}$. Нехай$h$ дорівнює висоті коробки.

Малюнок$\PageIndex{3}$

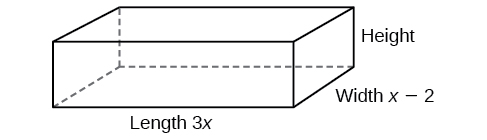
Тепер ми можемо записати рівняння, підставивши відомі значення в формулу об'єму прямокутного твердого тіла.

$$\begin{align*} V&=l{\cdot}w{\cdot}h \\ 3x^4−3x^3−33x^2+54x&=3x{\cdot}(x−2){\cdot}h \end{align*}$$

Щоб вирішити для$h$, спочатку розділіть обидві сторони на$3x$.

$$\dfrac{3x{\cdot}(x−2){\cdot}h}{3x}=\dfrac{3x^4−3x^3−33x^2+54x}{3x} \nonumber$$

$$(x-2)h=\dfrac{x^3-x^2-11x+18}{x-2} \nonumber$$

Тепер вирішуйте за$h$ допомогою синтетичного поділу.

$$h=\dfrac{x^3−x^2−11x+18}{x−2} \nonumber$$

\ [\ large {\ begin {масив} {c} -2\\\\\\ кінець {масив}} {
\ begin
{align*} &\\ [0pt]
& {\ begin {масив} {r|}\\ [0pt]\ [0pt]\ end {масив}
\\ [1pt] &\\ end {align*}}\\ [1pt]
&\\ end {align*}}\ [1pt] &\\ end {align*}\! \!
{\ begin {масив} {rrrr}
1 & -1 & -11
& 18\\ & 2 & -18\\
\ hline 1 & 1 & -9 & 0
\ кінець {масив}}
\ nonumber\]

Частка є,$x^2+x−9$ а залишок -$0.$ Висота твердого тіла є$x^2+x−9$.

Спробуйте! $\PageIndex{4}$

Площа прямокутника задається значенням$3x^3+14x^2−23x+6$. Ширина прямокутника задається за допомогою$x+6$. Знайдіть вираз для довжини прямокутника.

Рішення

$3x^2−4x+1$

Ключові рівняння

Алгоритм поділу$f(x)=d(x)q(x)+r(x)$ де$q(x){\neq}0$

Ключові поняття

• Поліноміальне довге ділення може бути використано для поділу многочлена на будь-який многочлен з рівним або нижчим ступенем.
• Алгоритм поділу говорить нам, що поліноміальний дивіденд може бути записаний як добуток дільника, а частка додається до залишку.
• Синтетичне ділення - це ярлик, який може бути використаний для поділу многочлена на біном у вигляді$x−k.$
• Поліноміальне поділ може бути використано для вирішення прикладних задач, включаючи площу та об'єм.

Виноски

$^1$Служба національних парків. «Статистика будівлі Меморіалу Лінкольна». www.nps.gov/linc/historycultu... statistics.htm. Доступ до 04.03.2014

Глосарій

Алгоритм поділу

заданий поліноміальний дивіденд$f(x)$ і ненульовий поліноміальний дільник,$d(x)$ де ступінь менше або дорівнює ступеня$f(x)$, існують унікальні поліноми$q(x)$ і$r(x)$ такі, що$f(x)=d(x)q(x)+r(x)$ де$q(x)$$r(x)$ частка і є$d(x)$ залишок. Залишок або дорівнює нулю, або має ступінь строго менше$d(x)$.

синтетичне поділ

метод швидкого доступу, який може бути використаний для поділу многочлена на біном форми$x−k$