2.7: Синтетичний відділ

Процес поліноміального довгого ділення (як процес числового довгого ділення) був дещо відокремлений від його логічних основ для більш ефективного методу отримання відповіді. Для окремих типів поліноміального довгого ділення ми можемо навіть зробити цю абстракцію на крок далі. Синтетичний поділ - це зручний ярлик для багаточленів довгих задач ділення, в яких ми ділимо на лінійний многочлен. Це означає, що найвищу силу$x$ ми ділимо на потреби повинні бути$x^{1}$. Це обмежує корисність синтетичного відділу, але це буде служити нам добре для певних цілей. Давайте розберемо, звідки беруться коефіцієнти в нашій відповіді, коли ми ділимо на лінійний многочлен:

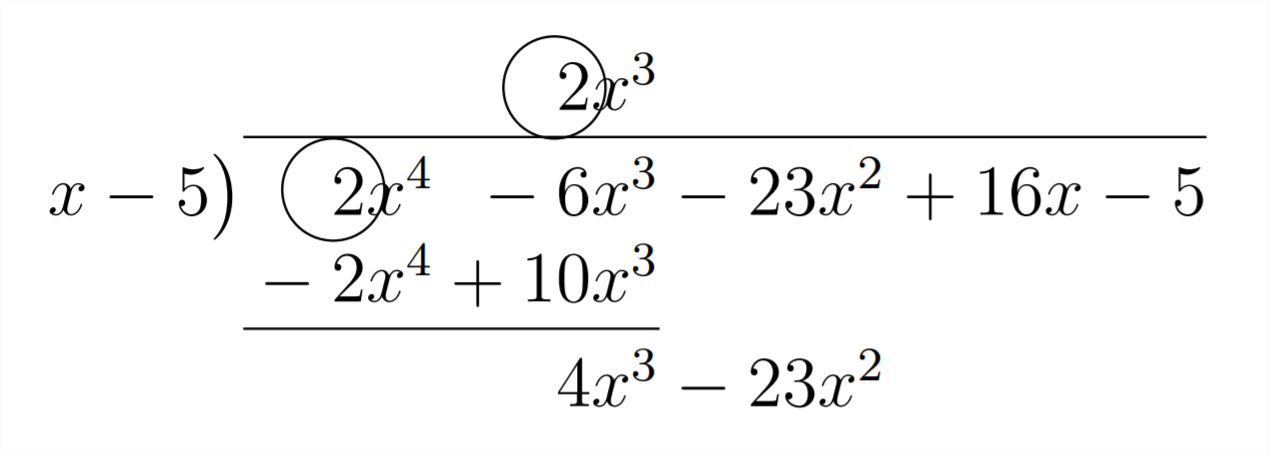
Зверніть увагу, що перший коефіцієнт у відповіді такий же, як перший коефіцієнт у поліномі, на який ми ділимо. Це тому, що ми ділимо на многочлен у формі$1 x^{1}-a .$ Це також робить силу першого члена у відповіді на одну меншу, ніж сила многочлена, на який ми ділимо. Давайте подивимося, звідки беруться наступні коефіцієнти у відповіді:

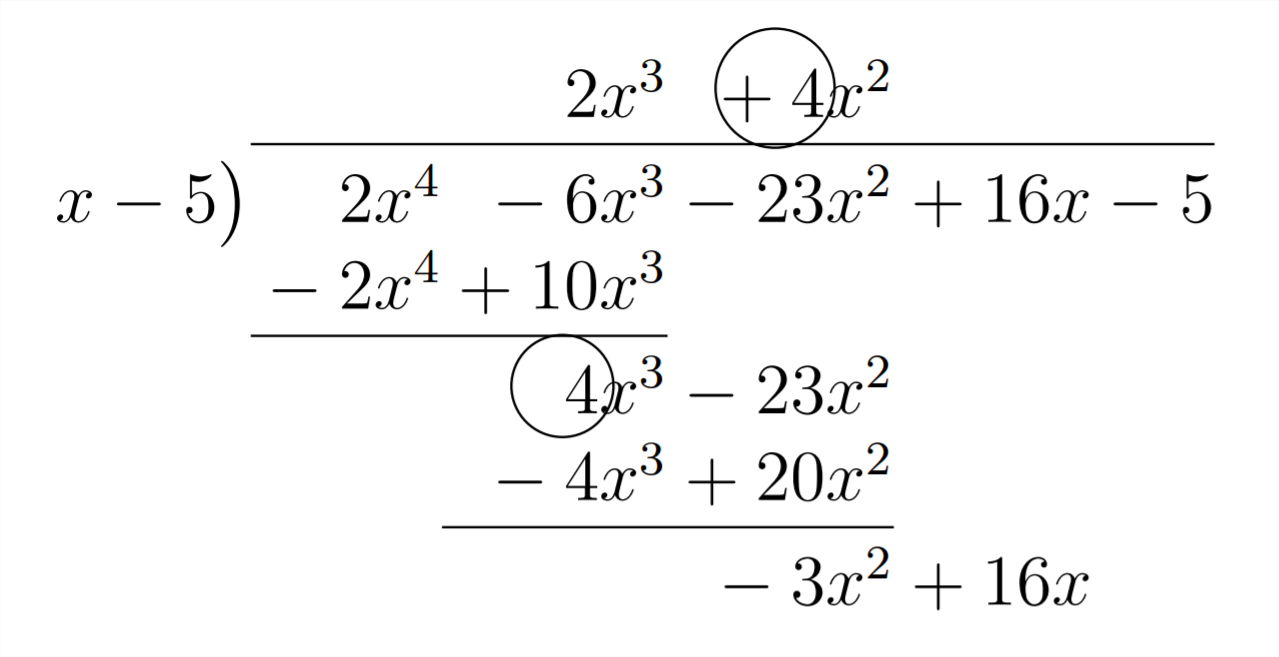
Наступний коефіцієнт у відповіді (4) походить від комбінації -6 і +10 прийшов від множення 2 у відповіді на 5 у$x-5 .$ дільнику Наступний коефіцієнт у відповіді буде$-3,$ який походить від множення 4 (у відповіді) на 5 (у дільнику)$+10 .$ і поєднуючи його з -23 в многочлені ми ділимо на:

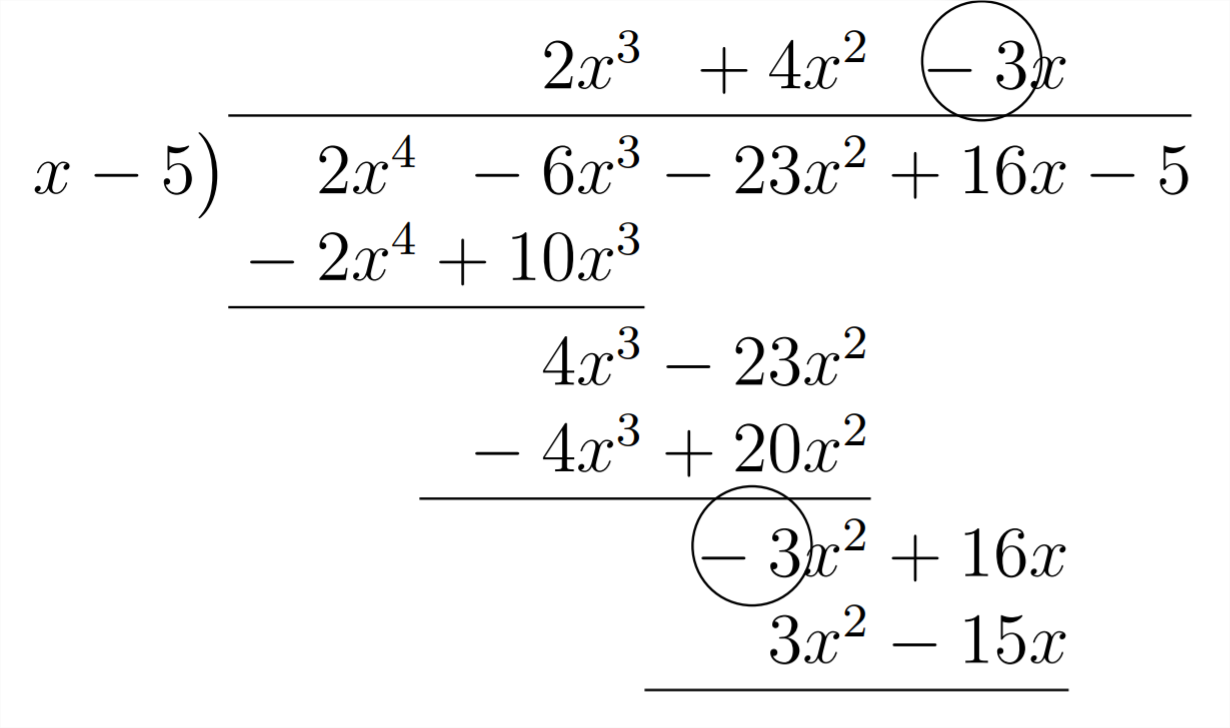
Остання частина нашої відповіді буде походити від множення -3 у відповіді на 5 в дільнику (роблячи -15) і поєднання цього з +16 в многочлені ми ділимо на:

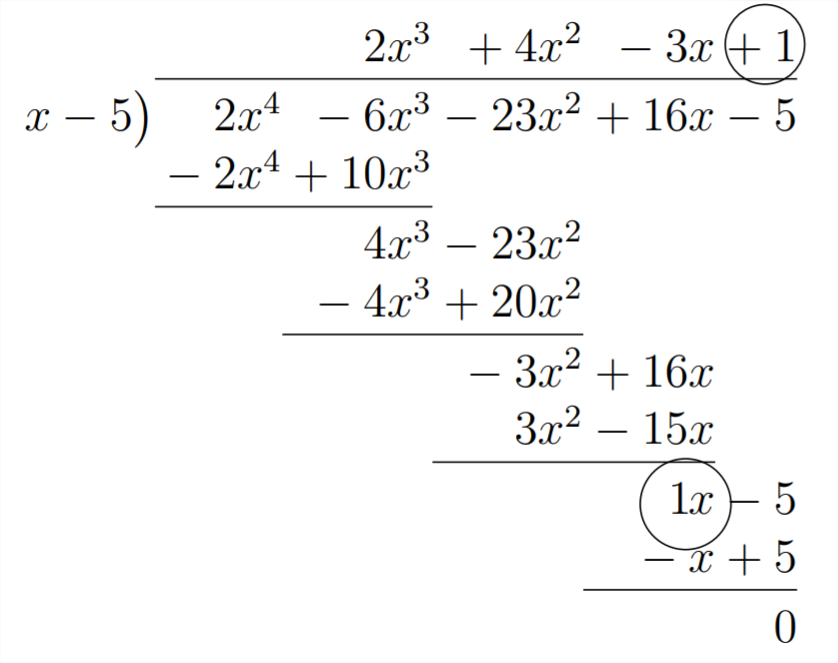
Процес Synthetic Division використовує ці відносини як ярлик для пошуку відповіді. Налаштування для проблеми синтетичного поділу показано нижче:

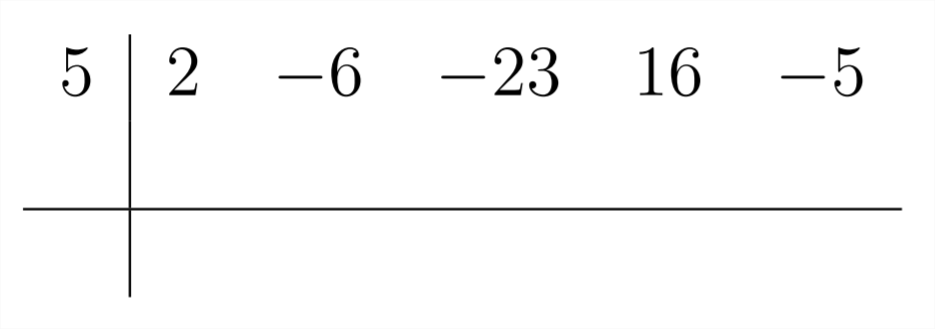
Ця настройка дозволяє нам завершити задачу ділення$\frac{2 x^{4}-6 x^{3}-23 x^{2}+16 x-5}{x-5}.$

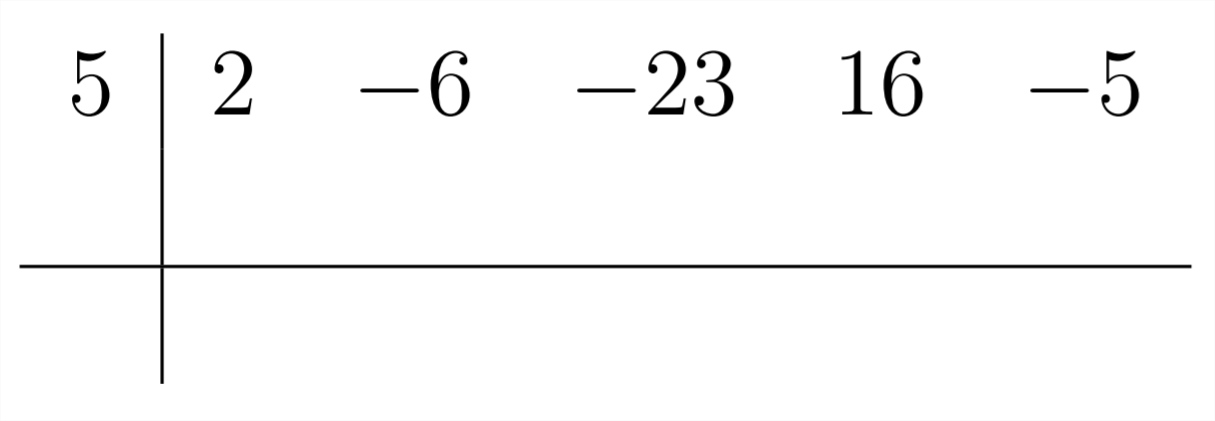
Перший коефіцієнт у відповіді такий самий, як і перший коефіцієнт у поліномі, на який ми ділимо:

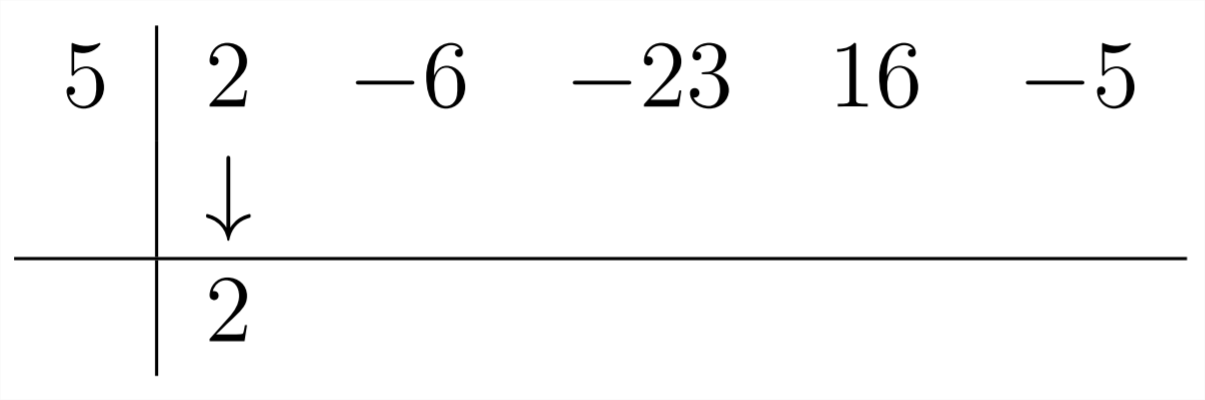
Щоб отримати наступний коефіцієнт, множимо 2 на 5, щоб отримати +10 і заповнити це під -6:

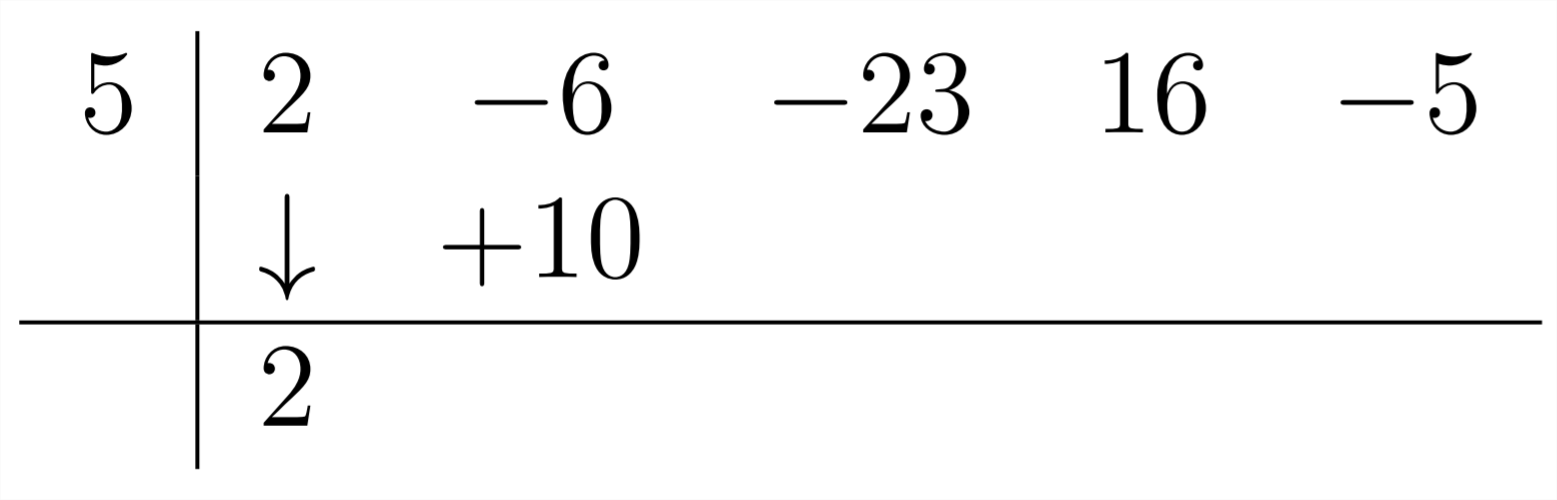
Потім,$-6+10=+4,$ який наступний коефіцієнт у відповідь:

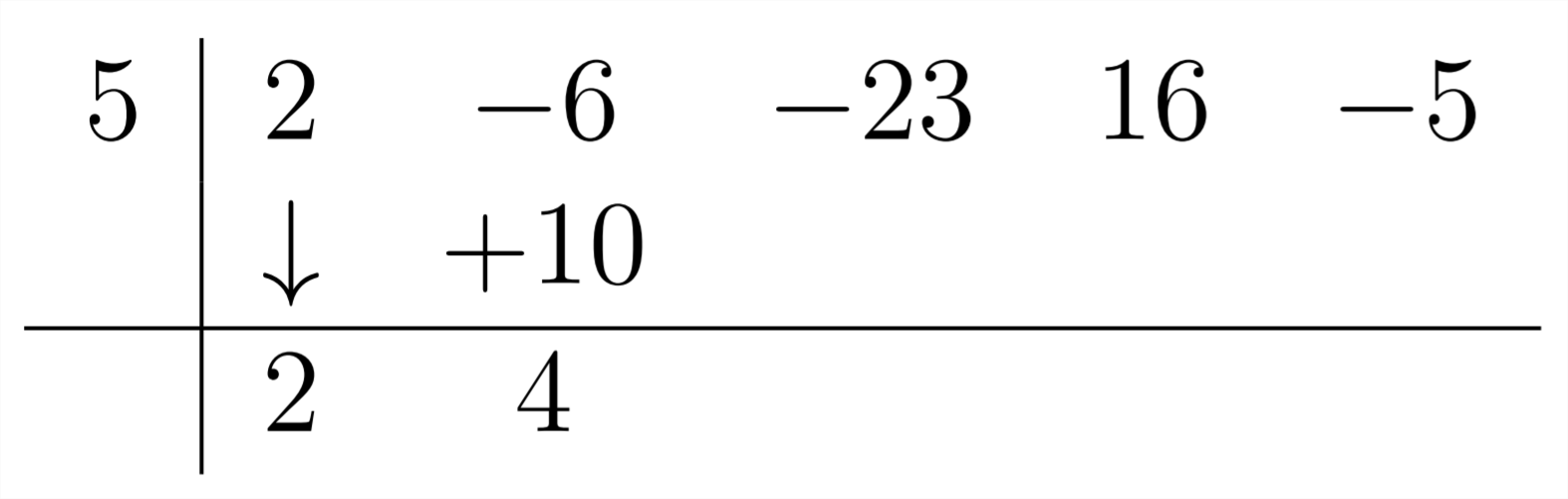
Потім, ми продовжуємо цей процес, множивши 4 на 5, щоб отримати 20 і поєднуючи це з$-23:-23+20=-3:$

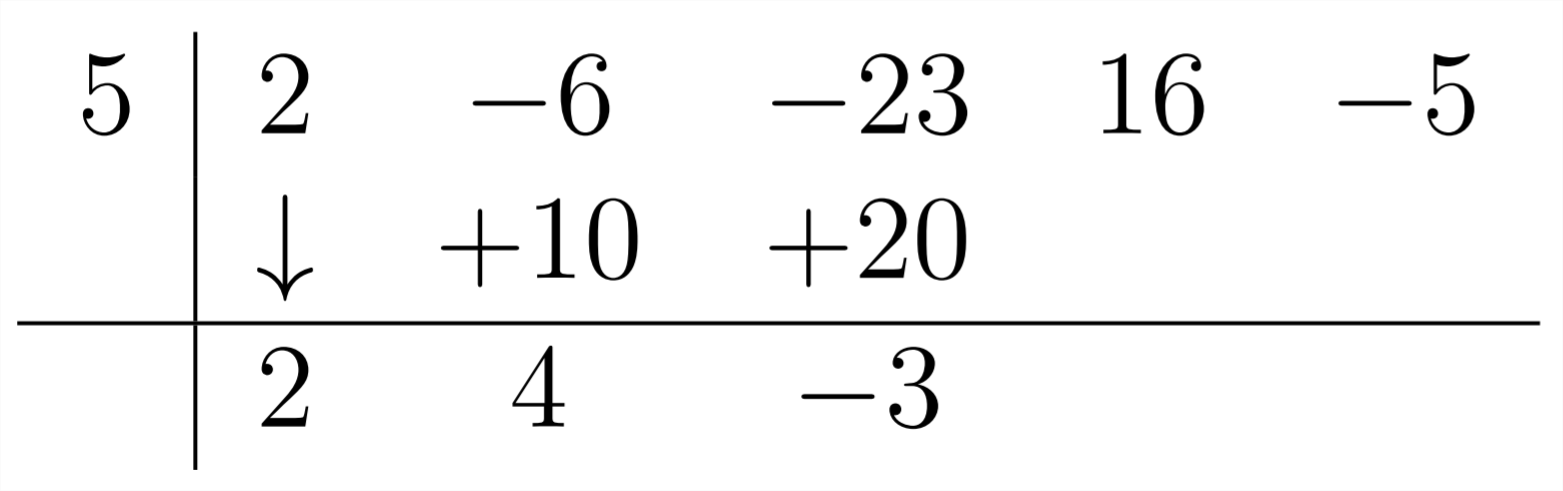
Далі множимо -3 на 5 і з'єднуємо отриманий -15 з 16:

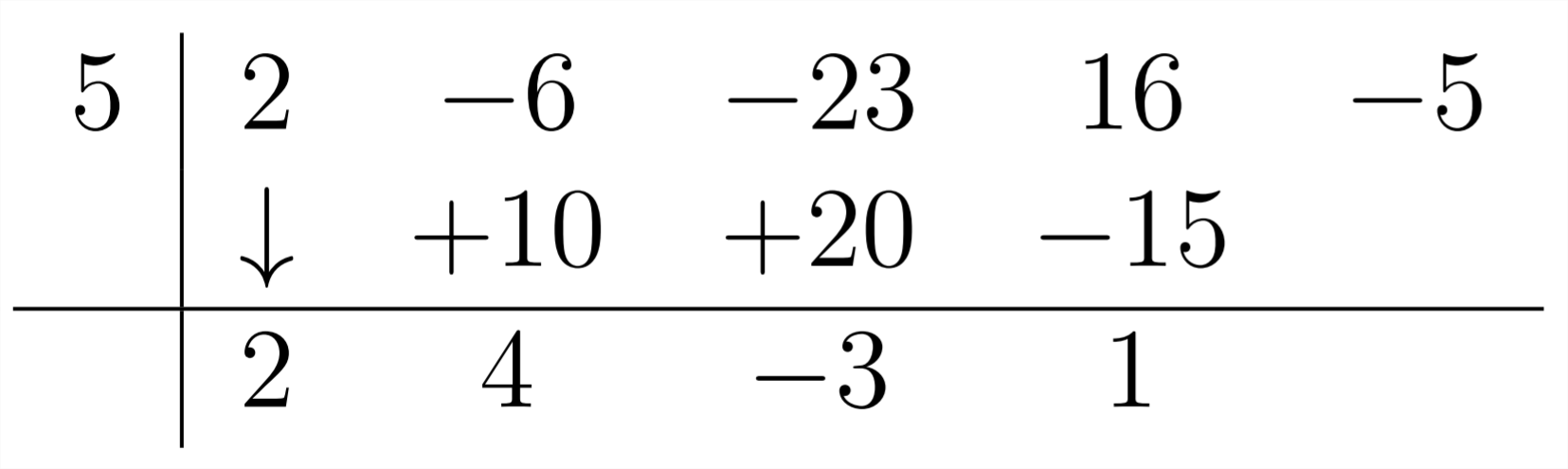
На останньому кроці помножте 1 раз на 5 і з'єднайте результат з -5 в задачі, щоб отримати нуль:

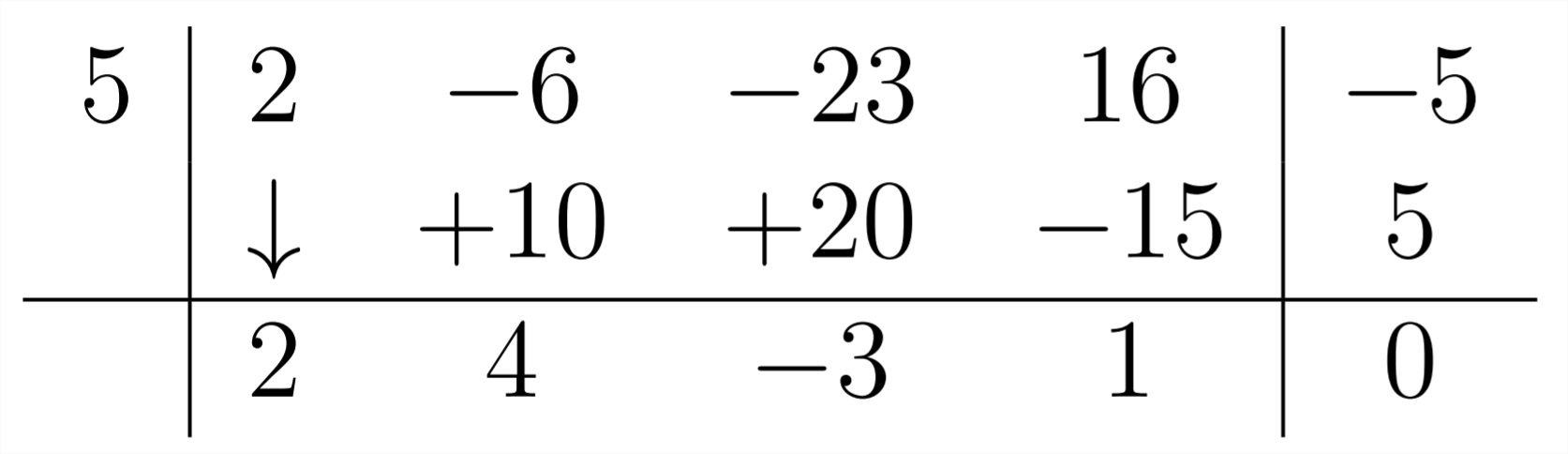
Цей останній коефіцієнт являє собою залишок - в даному випадку 0. Інші числівники у відповіді представляють коефіцієнти для степенів$x$ у відповіді. У крайньому правому куті знаходиться залишок, потім постійний$\left(x^{0}\right)$ термін, потім лінійний$\left(x^{1}\right)$ термін і так далі:

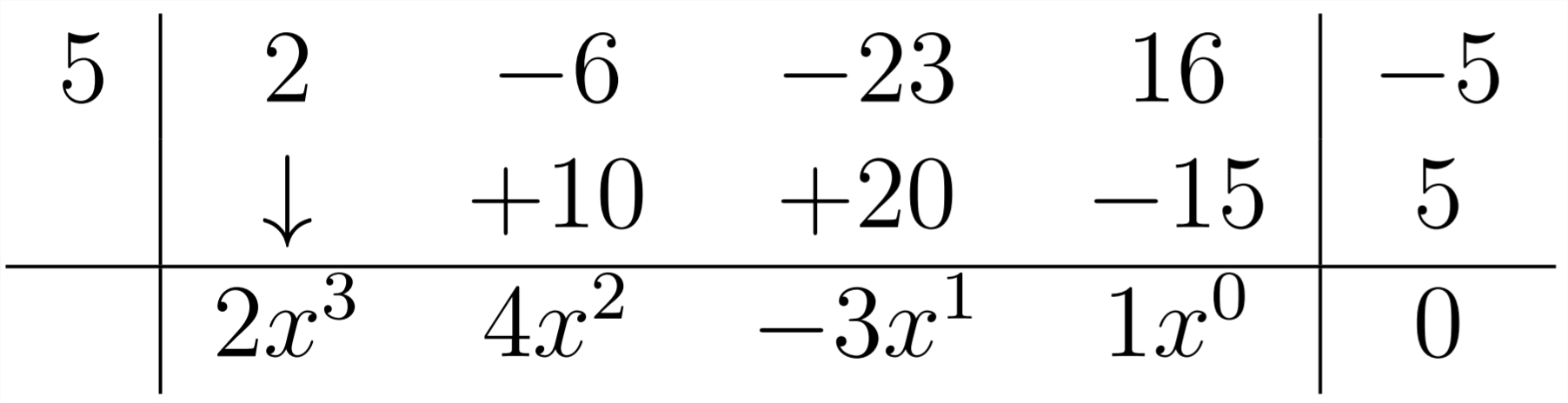
$\frac{2 x^{4}-6 x^{3}-23 x^{2}+16 x-5}{x-5}=2 x^{3}+4 x^{2}-3 x+1$
Давайте розглянемо інший

приклад: Приклад Use
Synthetic Поділ для поділу:
$\frac{3 x^{3}+5 x^{2}-9 x+9}{x+3}$
оскільки синтетичний відділ налаштований на поділ на$x-a$, якщо ми$x+3$ ділимо на, нам потрібно буде використовувати -3 у Синтетичному відділі:

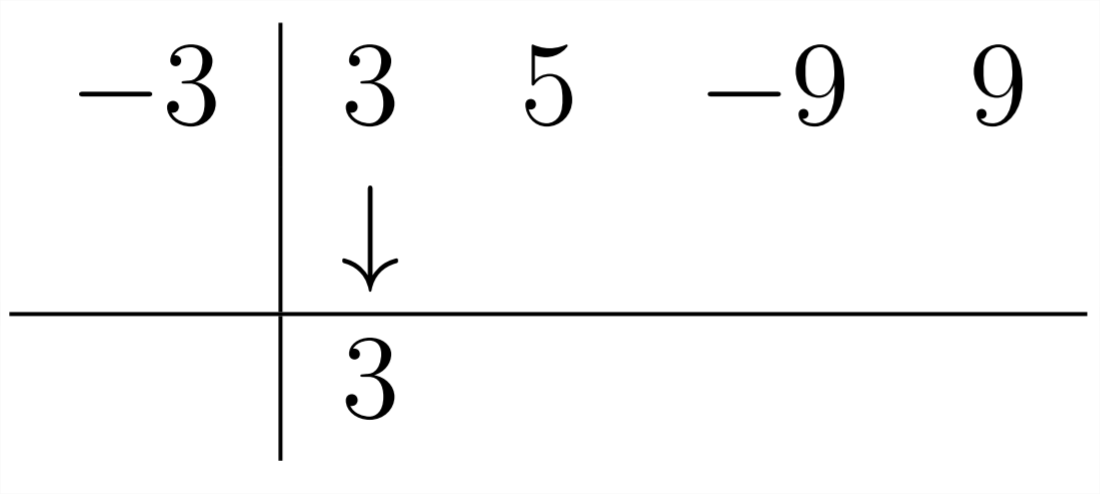
Тоді,$3 *-3=-9$

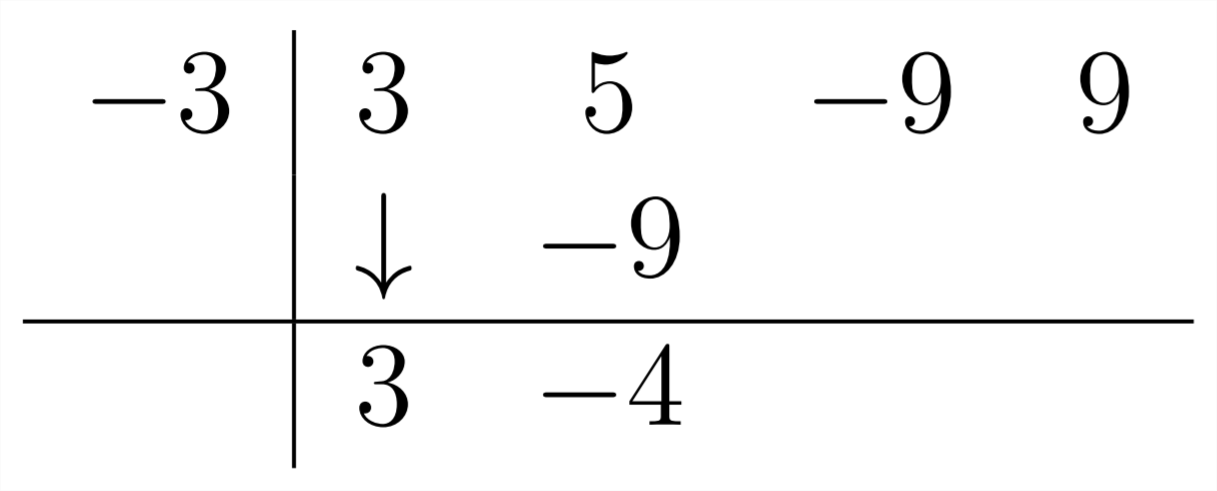
Далі,$-4 *-3=+12$

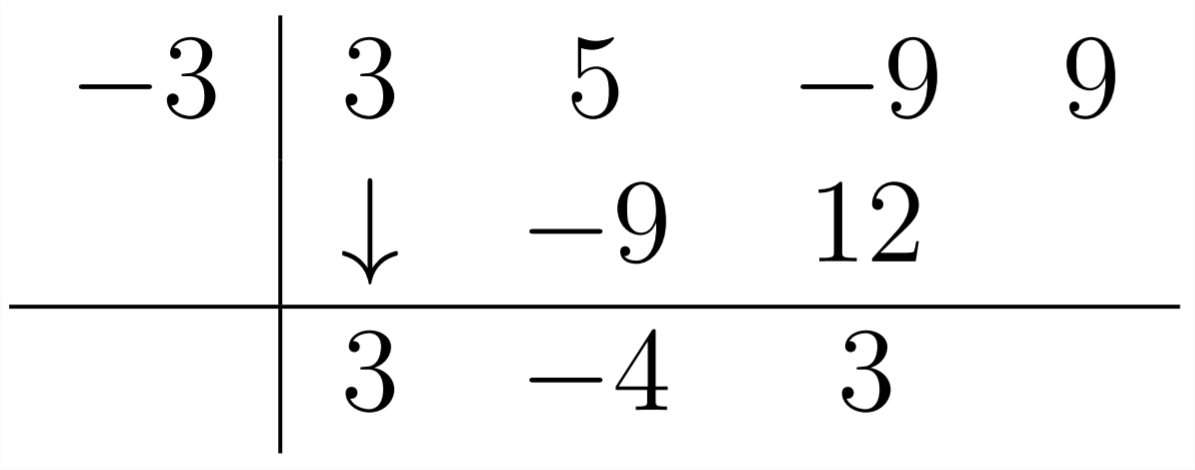
І цей приклад також має нульовий залишок:

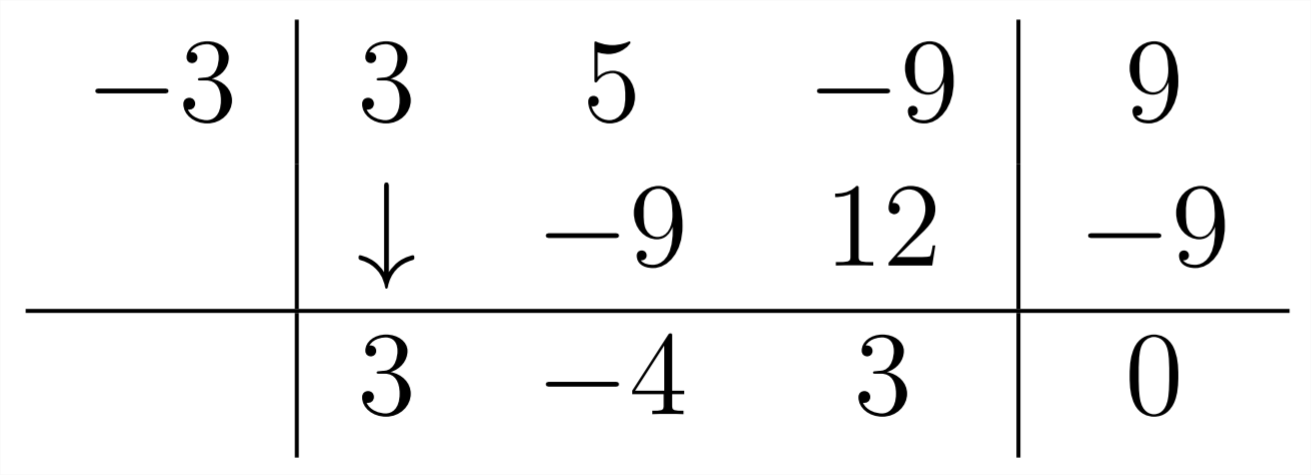
Відповідь тут$3 x^{2}-4 x+3$
\ [
\ frac {3 x^ {3} +5 x^ {2} -9 x+9} {x+3} =3 x^ {2} -4 x+3
\]
і
\ [
3 x^ {3} +5 x^ {2} -9 x+9 =( x+3)\ left (3 x^ {2} -4 x+3
\ праворуч)\]
Давайте розглянемо приклад, який трохи відрізняється.

Приклад
Використовуйте синтетичний поділ для поділу:
$\frac{6 x^{4}+x^{3}+9 x^{2}+x-2}{2 x+1}$
Синтетичний відділ створений для вирішення проблем, в яких ми ділимося на$1 x-a .$ Ясно, що в цьому прикладі це не так, однак ми можемо обійти це. Інший спосіб погляду на налаштування синтетичного поділу полягає в тому, що ми використовуємо число, яке є рішенням$x-a=0 .$ Коли ми розділили на$x-5,$ ми використовували
+5. Коли ми ділили на$x+3$, ми використовували$-3 .$ Отже, якщо ми збираємося розділити на$2 x+1,$ ми будемо використовувати$-\frac{1}{2}$ в синтетичному відділі:

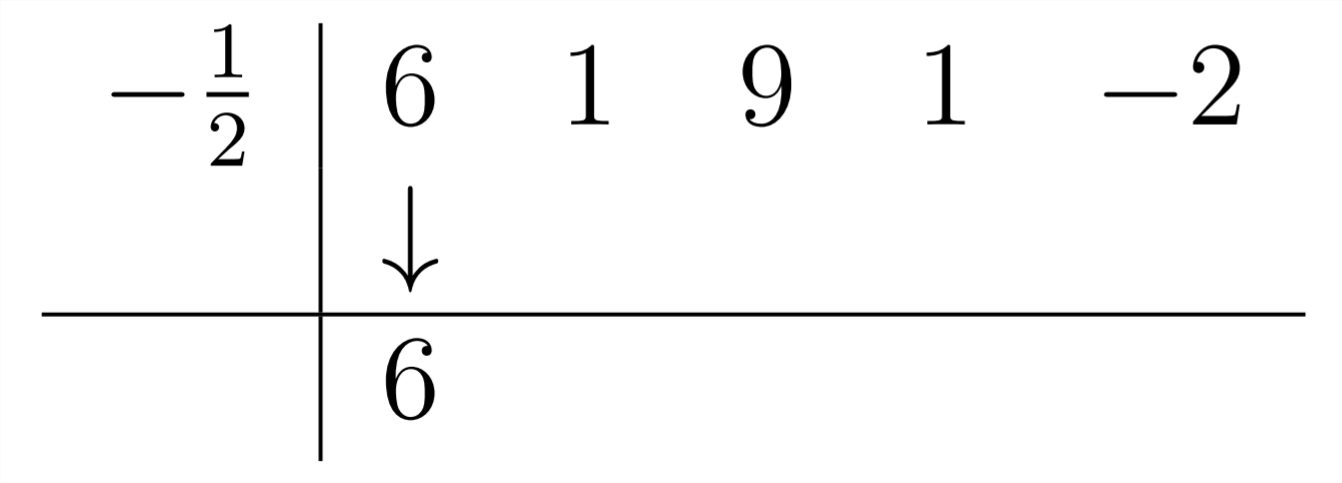
Потім, ми продовжуємо, як зазвичай:

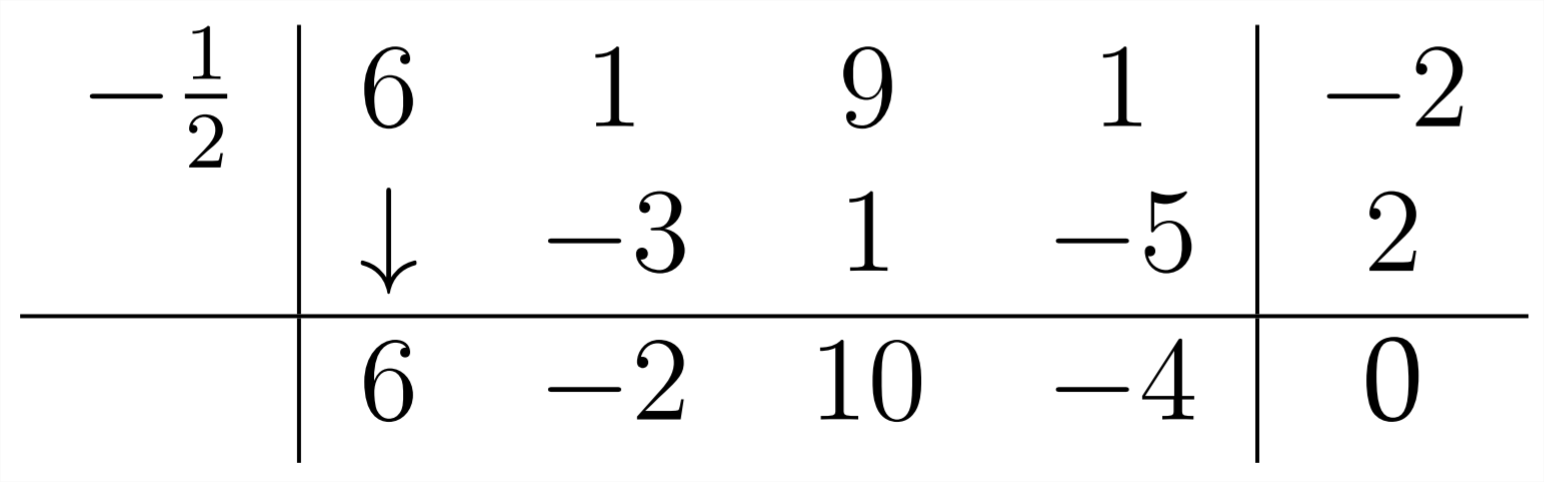
Зверніть увагу, що, знову ж таки, у нас є нуль залишок. Також зверніть увагу, що кожен коефіцієнт в нашій відповіді має загальний коефіцієнт$2,$ якого був коефіцієнт того,$x$ в$2 x+1,$ якому ми спочатку збиралися ділити на. Те, що ми зробили тут не ділення на,$2 x+1,$ а ділення на$x+\frac{1}{2}$
Отже, врешті-решт, наша робота говорить нам, що:

\ [\ frac {6 x^ {4} +x^ {3} +9 x^ {2} +x-2} {x+\ frac {1} {2}} =6 x^ {3} -2 x^ {2} +10 x-4
\]
і
\ [
6 x^ {4} +x^ {3} +9 x^ {2} +x-2 =\ left (x+\ frac {1} {2}\ праворуч)\ left (6 x^ {3} -2 x^ {2} +10 x-4\ праворуч)
\]
Зверніть увагу, що якщо ми визначимо загальний коефіцієнт 2 з нашої відповіді, ми можемо помножити його назад в$x+\frac{1}{2}$ і отримати відповідь на нашу оригінальну проблему:
\ [
\ почати {вирівняний}
6 x^ {4} +x^ {3} +9 x^ {2} +x-2 &=\ лівий (x+\ frac {1} {2}\ праворуч) 2\ ліворуч (3 x^ {3} -x^ {2} +5 x-2\ праворуч)\\
& =( 2 х+1)\ ліворуч (3 x ^ {3} -x^ {2} +5 2\ праворуч)
\ end {вирівняний}
\]
Це означає, що:
\ [
\ frac {6 x^ {4} +x^ {3} +9 x^ {2} +x-2} {2 x+1} =3 x^ {3} -x^ {2} +5 x-2
\]
Ще одна річ, щоб зрозуміти про синтетичний поділ, що якщо немає потужності$x$, то ви повинні включити нуль як коефіцієнт цієї потужності

Приклад
Використовуйте синтетичний поділ для поділу:
$\frac{x^{3}+4 x-6}{x-2}$
оскільки в поліномі, на$x^{2}$ який ми ділимо, ми введемо нуль як коефіцієнт для цього члена:

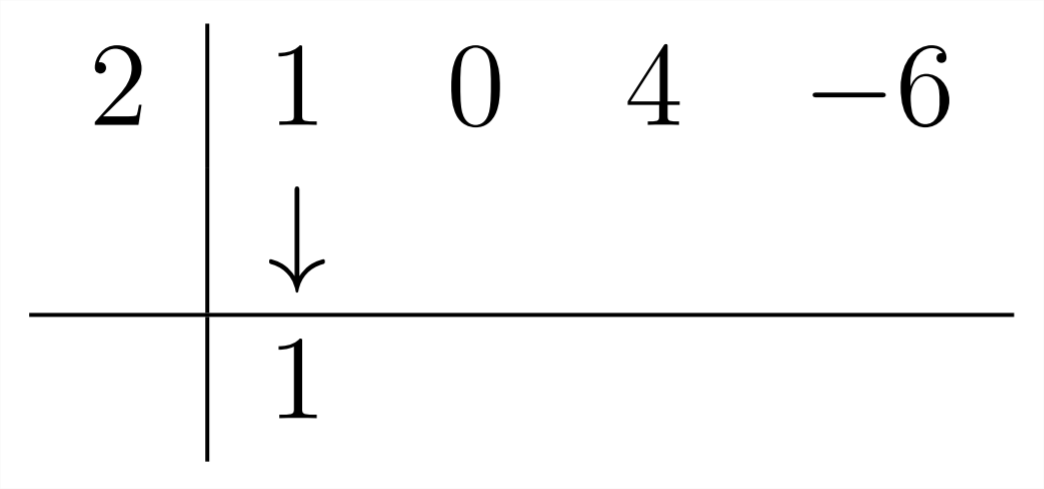
А потім продовжуйте, як завжди:

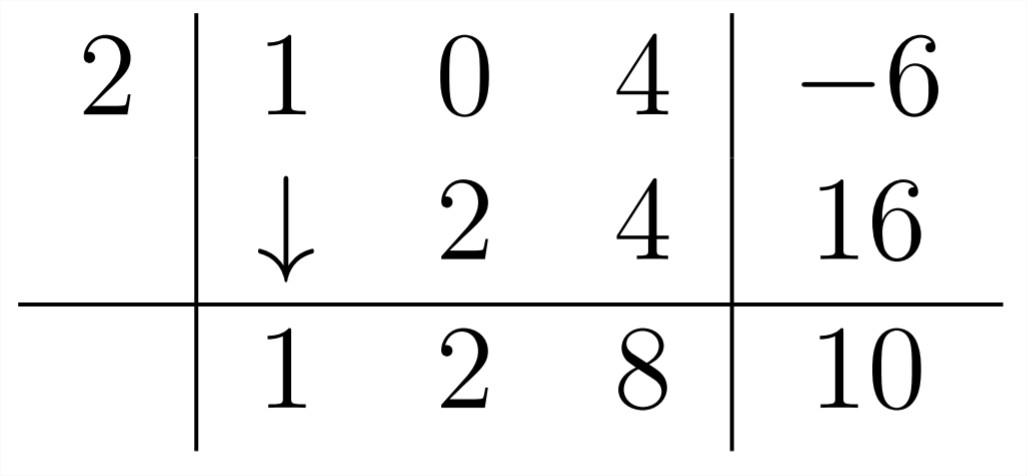
Отже, відповідь на цю проблему$x^{2}+2 x+8$

Вправи 2.7
Використовуйте синтетичний поділ, щоб знайти частку в кожній задачі.
1)$\frac{x^{3}-8 x^{2}+5 x+50}{x-5}$
2)$\frac{x^{3}+5 x^{2}-x-14}{x+2}$
3)$\frac{x^{3}+12 x^{2}+34 x-7}{x+7}$
4)$\frac{x^{3}-10 x^{2}+23 x-6}{x-3}$
5)$\frac{x^{4}-15 x^{2}+10 x+24}{x+4}$
6)$\frac{x^{4}-3 x^{3}+4 x^{2}-36}{x-3}$
7)$\frac{x^{4}-2 x^{3}-x+10}{x-2}$
8)$\frac{x^{4}-16 x^{2}-5 x-24}{x+4}$
9)$\frac{2 x^{4}-x^{3}+2 x-1}{2 x-1}$
10)$\frac{3 x^{4}+x^{3}-3 x+1}{3 x+1}$
11)$\frac{3 x^{4}-8 x^{3}+9 x^{2}-2 x-2}{3 x+1}$
12)$\frac{6 x^{4}-7 x^{3}+5 x^{2}-17 x+10}{3 x-2}$
13)$\frac{2 x^{3}+7 x^{2}+6 x-5}{2 x-1}$
14)$\frac{3 x^{4}-x^{3}-21 x^{2}-11 x+6}{3 x-1}$