1.5: Глава 1 Вправи з рішеннями
- Page ID
- 58062
У Вправи\(\PageIndex{1}\) -\(\PageIndex{8}\) знайдіть просту факторизацію заданого натурального числа.
Вправа\(\PageIndex{1}\)
80
- Відповідь
-
\(80=2 \cdot 2 \cdot 2 \cdot 2 \cdot 5\)
Вправа\(\PageIndex{2}\)
108
Вправа\(\PageIndex{3}\)
180
- Відповідь
-
\(180=2 \cdot 2 \cdot 3 \cdot 3 \cdot 5\)
Вправа\(\PageIndex{4}\)
160
Вправа\(\PageIndex{5}\)
128
- Відповідь
-
\(128=2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2\)
Вправа\(\PageIndex{6}\)
192
Вправа\(\PageIndex{7}\)
32
- Відповідь
-
\(32=2 \cdot 2 \cdot 2 \cdot 2 \cdot 2\)
Вправа\(\PageIndex{8}\)
72
У Вправи\(\PageIndex{9}\) -\(\PageIndex{16}\) перетворіть задане десяткове число в дріб.
Вправа\(\PageIndex{9}\)
0,648
- Відповідь
-
Є три знака після коми, так\(0.648=\frac{648}{1000}=\frac{81}{125}\)
Вправа\(\PageIndex{10}\)
0,62
Вправа\(\PageIndex{11}\)
0,240
- Відповідь
-
Є три знака після коми, так\(0.240=\frac{240}{1000}=\frac{6}{25}\)
Вправа\(\PageIndex{12}\)
0,90
Вправа\(\PageIndex{13}\)
0,14
- Відповідь
-
Є два знака після коми, так\(0.14=\frac{14}{100}=\frac{7}{50}\)
Вправа\(\PageIndex{14}\)
0,760
Вправа\(\PageIndex{15}\)
0.888
- Відповідь
-
Є три знака після коми, так\(0.888=\frac{888}{1000}=\frac{111}{125}\)
Вправа\(\PageIndex{16}\)
0,104
У Вправи\(\PageIndex{17}\) -\(\PageIndex{24}\) перетворіть задане повторюване десяткове число в дріб.
Вправа\(\PageIndex{17}\)
\(0 . \overline{27}\)
- Відповідь
-
Нехай\(x=0 . \overline{27} .\) потім\(100 x=27 . \overline{27} .\) віднімання по обидва боки цих рівнянь.
\[\begin{aligned} 100 x &=27 . \overline{27} \\ x &=0 . \overline{27} \end{aligned}\]
врожайність\(99 x=27 .\) Нарешті, вирішуйте для\(x\) шляхом ділення на\(99 : x=\frac{27}{99}=\frac{3}{11}\).
Вправа\(\PageIndex{18}\)
\(0 . \overline{171}\)
Вправа\(\PageIndex{19}\)
\(0 . \overline{24}\)
- Відповідь
-
Нехай\(x=0 . \overline{24} .\) потім\(100 x=24 . \overline{24} .\) Віднімання по обидва боки цих рівнянь\[\begin{aligned} 100 x &=24 . \overline{24} \\ x &=0 . \overline{24} \end{aligned}\]
врожайність\(99 x=24 .\) Нарешті, вирішуйте для,\(x\) діливши на\(99 : x=\frac{24}{99}=\frac{8}{33}\)
Вправа\(\PageIndex{20}\)
\(0 . \overline{882}\)
Вправа\(\PageIndex{21}\)
\(0 . \overline{84}\)
- Відповідь
-
Нехай\(x=0 . \overline{84} .\) потім\(100 x=84 . \overline{84} .\) Віднімання по обидва боки цих рівнянь
\[\begin{aligned} 100 x &=84 . \overline{.84} \\ x &=0 . \overline{84} \end{aligned}\]
врожайність\(99 x=84 .\) Нарешті, вирішуйте для,\(x\) діливши на\(99 : x=\frac{84}{99}=\frac{28}{33}\)
Вправа\(\PageIndex{22}\)
\(0 . \overline{384}\)
Вправа\(\PageIndex{23}\)
\(0 . \overline{63}\)
- Відповідь
-
Нехай\(x=0 . \overline{63} .\) потім\(100 x=63 . \overline{63} .\) Віднімання по обидва боки цих рівнянь
\[\begin{aligned} 100 x &=63 . \overline{63} \\ x &=0 . \overline{63} \end{aligned}\]
врожайність\(99 x=63 .\) Нарешті, вирішуйте для,\(x\) діливши на\(99 : x=\frac{63}{99}=\frac{7}{11}\)
Вправа\(\PageIndex{24}\)
\(0 . \overline{60}\)
Вправа\(\PageIndex{25}\)
Доведіть, що\(\sqrt{3}\) це нераціонально.
- Відповідь
-
Припустимо, що\(\sqrt{3}\) це раціонально. Потім його можна виразити у вигляді співвідношення двох цілих чисел p і q наступним чином:
\[\sqrt{3}=\frac{p}{q}\]
Квадрат з обох сторін,\[3=\frac{p^{2}}{q^{2}}\]
потім очистити рівняння дробів, помноживши обидві сторони на\(q^{2}\):
\[p^{2}=3 q^{2}\]
Тепер p і q кожен має свої унікальні прості факторизації. Обидва\(p^{2}\) і\(q^{2}\) мають парну кількість факторів у своїх простих факторизаціях. Але це суперечить рівнянню (1), тому що ліва сторона матиме парну кількість факторів у його простому факторизації, тоді як права сторона матиме непарну кількість факторів у його простому факторизації (є один додатковий 3 на правій стороні).
Тому наше припущення, яке\(\sqrt{3}\) було раціональним, є помилковим. Таким чином,\(\sqrt{3}\) є нераціональним.
Вправа\(\PageIndex{26}\)
Доведіть, що\(\sqrt{5}\) це нераціонально.
У Вправи\(\PageIndex{27}\) -\(\PageIndex{30}\) скопіюйте дану таблицю на домашній папір. У кожному рядку поставте галочку в кожному стовпчику, яка підходить. Тобто, якщо число на початку рядка раціональне, поставте галочку в раціональному стовпчику. Примітка: Більшість (але не всіх) рядків матимуть більше однієї галочки.
Вправа\(\PageIndex{27}\)
| \(\mathbb{N}\) | \(\mathbb{W}\) | \(\mathbb{Z}\) | \(\mathbb{Q}\) | \(\mathbb{R}\) | |
| 0 | |||||
| -2 | |||||
| -2/3 | |||||
| 0,15 | |||||
| \(0 . \overline{2}\) | |||||
| \(\sqrt{5}\) |
- Відповідь
-
\(\mathbb{N}\) \(\mathbb{W}\) \(\mathbb{Z}\) \(\mathbb{Q}\) \(\mathbb{R}\) 0 х х х х -2 х х х -2/3 х х 0,15 х х \(0 . \overline{2}\) х х \(\sqrt{5}\) х
Вправа\(\PageIndex{28}\)
| \(\mathbb{N}\) | \(\mathbb{W}\) | \(\mathbb{Z}\) | \(\mathbb{Q}\) | \(\mathbb{R}\) | |
| 10/2 | |||||
| \(\pi\) | |||||
| -6 | |||||
| \(0 . \overline{9}\) | |||||
| \(\sqrt{2}\) | |||||
| 0,37 |
Вправа\(\PageIndex{29}\)
| \(\mathbb{N}\) | \(\mathbb{W}\) | \(\mathbb{Z}\) | \(\mathbb{Q}\) | \(\mathbb{R}\) | |
| -4/3 | |||||
| 12 | |||||
| 0 | |||||
| \(\sqrt{11}\) | |||||
| \(1. \overline{3}\) | |||||
| 6/2 |
- Відповідь
-
\(\mathbb{N}\) \(\mathbb{W}\) \(\mathbb{Z}\) \(\mathbb{Q}\) \(\mathbb{R}\) -4/3 х х 12 х х х х х 0 х х х х \(\sqrt{11}\) х \(1. \overline{3}\) х х 6/2 х х х х х
Вправа\(\PageIndex{30}\)
| \(\mathbb{N}\) | \(\mathbb{W}\) | \(\mathbb{Z}\) | \(\mathbb{Q}\) | \(\mathbb{R}\) | |
| -3/5 | |||||
| \(\sqrt{10}\) | |||||
| 1,625 | |||||
| 10/2 | |||||
| 0/5 | |||||
| 11 |
У Вправи\(\PageIndex{31}\) -\(\PageIndex{42}\) розгляньте дане твердження і визначте, правда воно чи хибне. Напишіть речення, що пояснює вашу відповідь. Зокрема, якщо твердження помилкове, спробуйте навести приклад, який суперечить твердженню.
Вправа\(\PageIndex{31}\)
Всі натуральні числа є цілими числами.
- Відповідь
-
Правда. Єдина відмінність між двома множинами полягає в тому, що набір цілих чисел містить число 0.
Вправа\(\PageIndex{32}\)
Всі цілі числа є раціональними числами.
Вправа\(\PageIndex{33}\)
Всі раціональні числа є цілими числами.
- Відповідь
-
Помилкові. Наприклад, не\(\frac{1}{2}\) є цілим числом.
Вправа\(\PageIndex{34}\)
Всі раціональні числа є цілими числами.
Вправа\(\PageIndex{35}\)
Деякі натуральні числа нераціональні.
- Відповідь
-
Помилкові. Всі натуральні числа раціональні, а тому не ірраціональні.
Вправа\(\PageIndex{36}\)
Деякі цілі числа нераціональні.
Вправа\(\PageIndex{37}\)
Деякі дійсні числа нераціональні.
- Відповідь
-
Правда. Наприклад, π і √2 - дійсні числа, які є ірраціональними.
Вправа\(\PageIndex{38}\)
Всі цілі числа є дійсними числами.
Вправа\(\PageIndex{39}\)
Всі цілі числа є раціональними числами.
- Відповідь
-
Правда. Кожне ціле число b можна записати як дріб b/1.
Вправа\(\PageIndex{40}\)
Ніякі раціональні числа не є натуральними числами.
Вправа\(\PageIndex{41}\)
Ніякі дійсні числа не є цілими числами.
- Відповідь
-
Помилкові. Наприклад, 2 - це дійсне число, яке також є цілим числом.
Вправа\(\PageIndex{42}\)
Всі цілі числа є натуральними числами.
У Вправи\(\PageIndex{43}\) -\(\PageIndex{54}\) розв'яжіть кожне з заданих рівнянь для x.
Вправа\(\PageIndex{43}\)
45х+ 12 = 0
- Відповідь
-
\[\begin{aligned} & 45 x+12=0 \\ \Longrightarrow \quad & 45 x=-12 \\ \Longrightarrow \quad& x=-\frac{12}{45}=-\frac{4}{15} \end{aligned}\]
Вправа\(\PageIndex{44}\)
76х − 55 = 0
Вправа\(\PageIndex{45}\)
x − 7 = −6х+ 4
- Відповідь
-
\[\begin{aligned} & x-7=-6 x+4 \\ \Longrightarrow \quad & x+6 x=4+7 \\ \Longrightarrow \quad & 7 x=11 \\ \Longrightarrow \quad & x=\frac{11}{7} \end{aligned}\]
Вправа\(\PageIndex{46}\)
−26х+ 84 = 48
Вправа\(\PageIndex{47}\)
37х + 39 = 0
- Відповідь
-
\[\begin{aligned} & 37 x+39=0 \\ \Longrightarrow\quad & 37 x=-39 \\ \Longrightarrow\quad & x=-\frac{39}{37} \end{aligned}\]
Вправа\(\PageIndex{48}\)
−48х + 95 = 0
Вправа\(\PageIndex{49}\)
74х− 6 = 91
- Відповідь
-
\[\begin{aligned} & 74 x-6=91 \\ \Longrightarrow\quad & 74 x=97 \\ \Longrightarrow\quad & x=\frac{97}{74} \end{aligned}\]
Вправа\(\PageIndex{50}\)
−7х+ 4 = −6
Вправа\(\PageIndex{51}\)
−88х+13 = −21
- Відповідь
-
\[\begin{aligned} &-88 x+13=-21 \\ \Longrightarrow\quad &-88 x=-34 \\ \Longrightarrow \quad & x=\frac{-34}{-88}=\frac{17}{44} \end{aligned}\]
Вправа\(\PageIndex{52}\)
−14х − 81 = 0
Вправа\(\PageIndex{53}\)
19х + 35 = 10
- Відповідь
-
\[\begin{aligned} & 19 x+35=10 \\ \Longrightarrow\quad & 19 x=-25 \\ \Longrightarrow\quad & x=-\frac{25}{19} \end{aligned}\]
Вправа\(\PageIndex{54}\)
−2х+ 3 = −5х − 2
У Вправи\(\PageIndex{55}\) -\(\PageIndex{66}\) розв'яжіть кожне з заданих рівнянь для x.
Вправа\(\PageIndex{55}\)
6 − 3 (х + 1) = −4 (х + 6) + 2
- Відповідь
-
\[\begin{aligned} & 6-3(x+1)=-4(x+6)+2 \\ \Longrightarrow\quad & 6-3 x-3=-4 x-24+2 \\ \Longrightarrow\quad &-3 x+3=-4 x-22 \\ \Longrightarrow\quad &-3 x+4 x=-22-3 \\ \Longrightarrow\quad & x=-25 \end{aligned}\]
Вправа\(\PageIndex{56}\)
(8х+ 3) − (2х+ 6) = −5х+ 8
Вправа\(\PageIndex{57}\)
−7 − (5x − 3) = 4 (7х + 2)
\[\begin{aligned} &-7-(5 x-3)=4(7 x+2) \\ \Longrightarrow\quad &-7-5 x+3=28 x+8 \\ \Longrightarrow\quad &-5 x-4=28 x+8 \\ \Longrightarrow\quad &-5 x-28 x=8+4 \\ \Longrightarrow\quad &-33 x=12 \\ \Longrightarrow\quad & x=-\frac{12}{33}=-\frac{4}{11} \end{aligned}\]
Вправа\(\PageIndex{58}\)
−3 − 4 (x + 1) = 2 (х + 4) + 8
Вправа\(\PageIndex{59}\)
9 − (6x − 8) = −8 (6х − 8)
- Відповідь
-
\[\begin{aligned} & 9-(6 x-8)=-8(6 x-8) \\ \Longrightarrow \quad & 9-6 x+8=-48 x+64 \\ \Longrightarrow\quad &-6 x+17=-48 x+64 \\ \Longrightarrow\quad &-6 x+48 x=64-17 \\ \Longrightarrow\quad & 42 x=47 \\ \Longrightarrow\quad & x=\frac{47}{42} \end{aligned}\]
Вправа\(\PageIndex{60}\)
−9 − (7x − 9) = −2 (−3x + 1)
Вправа\(\PageIndex{61}\)
(3x − 1) − (7x − 9) = −2x − 6
- Відповідь
-
\[\begin{aligned} &(3 x-1)-(7 x-9)=-2 x-6 \\ \Longrightarrow\quad & 3 x-1-7 x+9=-2 x-6 \\ \Longrightarrow\quad &-4 x+8=-2 x-6 \\ \Longrightarrow\quad &-4 x+2 x=-6-8 \\ \Longrightarrow\quad &-2 x=-14 \\ \Longrightarrow\quad & x=7 \end{aligned}\]
Вправа\(\PageIndex{62}\)
−8 − 8 (x − 3) = 5 (x + 9) + 7
Вправа\(\PageIndex{63}\)
(7x − 9) − (9х + 4) = −3х + 2
- Відповідь
-
\[\begin{aligned} &(7 x-9)-(9 x+4)=-3 x+2 \\ \Longrightarrow\quad & 7 x-9-9 x-4=-3 x+2 \\ \Longrightarrow\quad &-2 x-13=-3 x+2 \\ \Longrightarrow\quad &-2 x+3 x=2+13 \\ \Longrightarrow\quad & x=15 \end{aligned}\]
Вправа\(\PageIndex{64}\)
(−4х − 6) + (−9х + 5) = 0
Вправа\(\PageIndex{65}\)
−5 − (9х + 4) = 8 (−7х − 7)
- Відповідь
-
\[\begin{array}{ll}{} & {-5-(9 x+4)=8(-7 x-7)} \\ {\Longrightarrow} & {-5-9 x-4=-56 x-56} \\ {\Longrightarrow} & {-9 x-9=-56 x-56} \\ {\Longrightarrow} & {-9 x+56 x=-56+9} \\ {\Longrightarrow} & {47 x=-47} \\ {\Longrightarrow} & {x=-1}\end{array}\]
Вправа\(\PageIndex{66}\)
(8x − 3) + (−3x + 9) = −4х − 7
У Вправи\(\PageIndex{67}\) -\(\PageIndex{78}\) розв'яжіть кожне з заданих рівнянь для х Перевірте свої рішення за допомогою калькулятора.
Вправа\(\PageIndex{67}\)
−3.7x − 1 = 8.2x − 5
- Відповідь
-
Спочатку очистіть десяткові числа, помноживши на 10.
\[\begin{aligned} &-3.7 x-1=8.2 x-5 \\ \Longrightarrow\quad &-37 x-10=82 x-50 \\ \Longrightarrow\quad &-37 x-82 x=-50+10 \\ \Longrightarrow\quad &-119 x=-40 \\ \Longrightarrow\quad & x=\frac{40}{119} \end{aligned}\]
Ось перевірка рішень на графічному калькуляторі. Ліва частина рівняння оцінюється при розв'язці в (а), права частина рівняння оцінюється при розв'язку в (b). Зверніть увагу, що вони збігаються.

Вправа\(\PageIndex{68}\)
8.48х − 2,6 = −7,17х − 7,1
Вправа\(\PageIndex{69}\)
\(-\frac{2}{3} x+8=\frac{4}{5} x+4\)
- Відповідь
-
Спочатку очистіть дроби, помноживши на 15.
\[\begin{aligned} &-\frac{2}{3} x+8=\frac{4}{5} x+4 \\ \Longrightarrow\quad &-10 x+120=12 x+60 \\ \Longrightarrow\quad &-10 x-12 x=60-120 \\ \Longrightarrow\quad &-22 x=-60 \\ \Longrightarrow\quad & x=\frac{-60}{-22}=\frac{30}{11} \end{aligned}\]
Ось перевірка рішень на графічному калькуляторі. Ліва частина рівняння оцінюється при розв'язці в (а), права частина рівняння оцінюється при розв'язку в (b). Зверніть увагу, що вони збігаються.

Вправа\(\PageIndex{70}\)
−8,4х = −4,8х+ 2
Вправа\(\PageIndex{71}\)
\(-\frac{3}{2} x+9=\frac{1}{4} x+7\)
- Відповідь
-
Спочатку очистіть дроби, помноживши на 4.
\[\begin{aligned} &-\frac{3}{2} x+9=\frac{1}{4} x+7 \\ \Longrightarrow\quad &-6 x+36=x+28 \\ \Longrightarrow\quad &-6 x-x=28-36 \\ \Longrightarrow\quad &-7 x=-8 \\ \Longrightarrow\quad & x=\frac{8}{7} \end{aligned}\]
Ось перевірка рішень на графічному калькуляторі. Ліва частина рівняння оцінюється при розв'язці в (а), права частина рівняння оцінюється при розв'язку в (b). Зверніть увагу, що вони збігаються.

Вправа\(\PageIndex{72}\)
2.9x − 4 = 0.3х − 8
Вправа\(\PageIndex{73}\)
5,45х + 4,4 = 1,12х + 1,6
- Відповідь
-
Спочатку очистіть десяткові числа, помноживши на 100.
\[\begin{aligned} & 5.45 x+4.4=1.12 x+1.6 \\ \Longrightarrow\quad & 545 x+440=112 x+160 \\ \Longrightarrow\quad & 545 x-112 x=160-440 \\ \Longrightarrow\quad & 433 x=-280 \\ \Longrightarrow\quad & x=-\frac{280}{433} \end{aligned}\]
Ось перевірка рішень на графічному калькуляторі. Ліва частина рівняння оцінюється при розв'язці в (а), права частина рівняння оцінюється при розв'язку в (b). Зверніть увагу, що вони збігаються.

Вправа\(\PageIndex{74}\)
\(-\frac{1}{4} x+5=-\frac{4}{5} x-4\)
Вправа\(\PageIndex{75}\)
\(-\frac{3}{2} x-8=\frac{2}{5} x-2\)
- Відповідь
-
Спочатку очистіть дроби, помноживши на 10. \[\begin{aligned} &-\frac{3}{2} x-8=\frac{2}{5} x-2 \\ \Longrightarrow\quad &-15 x-80=4 x-20 \\ \Longrightarrow\quad &-15 x-4 x=-20+80 \\ \Longrightarrow\quad &-19 x=60 \\ \Longrightarrow\quad & x=-\frac{60}{19} \end{aligned}\]
Ось перевірка рішень на графічному калькуляторі. Ліва частина рівняння оцінюється при розв'язці в (а), права частина рівняння оцінюється при розв'язку в (b). Зверніть увагу, що вони збігаються.

Вправа\(\PageIndex{76}\)
\(-\frac{4}{3} x-8=-\frac{1}{4} x+5\)
Вправа\(\PageIndex{77}\)
−4.34x − 5,3 = 5,45х − 8,1
- Відповідь
-
Спочатку очистіть десяткові числа, помноживши на 100.
\[\begin{aligned} &-4.34 x-5.3=5.45 x-8.1 \\ \Longrightarrow\quad &-434 x-530=545 x-810 \\ \Longrightarrow\quad &-434 x-545 x=-810+530 \\ \Longrightarrow\quad &-979 x=-280 \\ \Longrightarrow\quad & x=\frac{280}{979} \end{aligned}\]
Ось перевірка рішень на графічному калькуляторі. Ліва частина рівняння оцінюється при розв'язці в (а), права частина рівняння оцінюється при розв'язку в (b). Зверніть увагу, що вони збігаються.

Вправа\(\PageIndex{78}\)
\(\frac{2}{3} x-3=-\frac{1}{4} x-1\)
У Вправах\(\PageIndex{79}\) -50 розв'яжіть кожне з заданих рівнянь для зазначеної змінної.
Вправа\(\PageIndex{79}\)
P = ІРТ для R
- Відповідь
-
\[\begin{aligned} & P=I R T \\ \Longrightarrow\quad & P=(I T) R \\ \Longrightarrow\quad & \frac{P}{I T}=\frac{(I T) R}{I T} \\ \Longrightarrow\quad & \frac{P}{I T}=R \end{aligned}\]
Вправа\(\PageIndex{80}\)
d = vt для т
Вправа\(\PageIndex{81}\)
\(v=v_{0}+a t\)для\(a\)
- Відповідь
-
\[\begin{aligned} & v=v_{0}+a t \\ \Longrightarrow\quad & v-v_{0}=a t \\ \Longrightarrow\quad & \frac{v-v_{0}}{t}=a \end{aligned}\]
Вправа\(\PageIndex{82}\)
\(x=v_{0}+v t\)для\(v\)
Вправа\(\PageIndex{83}\)
Ax+ By = C для y
- Відповідь
-
\[\begin{aligned} & A x+B y=C \\ \Longrightarrow\quad & B y=C-A x \\ \Longrightarrow\quad & y=\frac{C-A x}{B} \end{aligned}\]
Вправа\(\PageIndex{84}\)
y = mx + б для х
Вправа\(\PageIndex{85}\)
\(A=\pi r^{2}\)для\(\pi\)
- Відповідь
-
\[\begin{aligned} A &=\pi r^{2} \\ \Longrightarrow \quad \frac{A}{r^{2}} &=\pi \end{aligned}\]
Вправа\(\PageIndex{86}\)
\(S=2 \pi r^{2}+2 \pi r h\)для\(h\)
Вправа\(\PageIndex{87}\)
\(F=\frac{k q q_{0}}{r^{2}}\)для\(k\)
- Відповідь
-
\[\begin{aligned} & F=\frac{k q q_{0}}{r^{2}} \\ \Longrightarrow\quad & F r^{2}=k q q_{0} \\ \Longrightarrow\quad & \frac{F r^{2}}{q q_{0}}=k \end{aligned}\]
Вправа\(\PageIndex{88}\)
\(C=\frac{Q}{m T}\)для\(T\)
Вправа\(\PageIndex{89}\)
\(\frac{V}{t}=k\)для\(t\)
- Відповідь
-
\[\begin{aligned} & \frac{V}{t}=k \\ \Longrightarrow\quad & V=k t \\ \Longrightarrow\quad & \frac{V}{k}=t \end{aligned}\]
Вправа\(\PageIndex{90}\)
\(\lambda=\frac{h}{m v}\)для\(v\)
Вправа\(\PageIndex{91}\)
\(\frac{P_{1} V_{1}}{n_{1} T_{1}}=\frac{P_{2} V_{2}}{n_{2} T_{2}}\)для\(V_{2}\)
- Відповідь
-
Перехресний множимо, потім ділимо на коефіцієнт\(V_{2}\).
\[\begin{aligned} & \frac{P_{1} V_{1}}{n_{1} T_{1}}=\frac{P_{2} V_{2}}{n_{2} T_{2}} \\ \Longrightarrow\quad & n_{2} P_{1} V_{1} T_{2}=n_{1} P_{2} V_{2} T_{1} \\ \Longrightarrow\quad & \frac{n_{2} P_{1} V_{1} T_{2}}{n_{1} P_{2} T_{1}}=V_{2} \end{aligned}\]
Вправа\(\PageIndex{92}\)
\(\pi=\frac{n R T}{V} i\)для\(n\)
Вправа\(\PageIndex{93}\)
Прив'яжіть кульку до нитки і кружьте його по колу з постійною швидкістю. Відомо, що прискорення кулі відбувається безпосередньо до центру кола і задається формулою,\[a=\frac{v^{2}}{r}\] де a - прискорення, v - швидкість кулі, а r - радіус кола руху.
i. розв'яжіть формулу (1) для r.
II. З огляду на, що прискорення кулі дорівнює 12 м/с2, а швидкість дорівнює 8 м/с, знайдіть радіус кола руху.
- Відповідь
-
Перехресний множимо, потім ділимо на коефіцієнт r.
\[\begin{aligned} a &=\frac{v^{2}}{r} \\ a r &=v^{2} \\ r &=\frac{v^{2}}{a} \end{aligned}\]
Щоб знайти радіус, підставляємо прискорення\(a=12 \mathrm{m} / \mathrm{s}^{2}\) і швидкість v = 8 м/с.
\[r=\frac{v^{2}}{a}=\frac{(8)^{2}}{12}=\frac{64}{12}=\frac{16}{3}\]
Значить, радіус дорівнює\(r=16 / 3 \mathrm{m},\) або 5\(\frac{1}{3}\) метрів.
Вправа\(\PageIndex{94}\)
Частка рухається уздовж лінії з постійним прискоренням. Відомо, що швидкість частинки, як функція кількості часу, що пройшов, задається рівнянням
\[v=v_{0}+a t\]де v - швидкість в момент t, v0 - початкова швидкість частинки (в момент часу t = 0), а - прискорення частинки.
i. розв'яжіть формулу (2) для t.
II. Ви знаєте, що поточна швидкість частинки становить 120 м/с, ви також знаєте, що початкова швидкість була 40 м/с, а прискорення було постійним\(a=2 \mathrm{m} / \mathrm{s}^{2}\). Скільки часу пішло частинці, щоб досягти своєї поточної швидкості?
Вправа\(\PageIndex{95}\)
Як і Універсальний закон тяжіння Ньютона, сила тяжіння (відштовхування) між двома несхожими (подібними) зарядженими частинками пропорційна добутку зарядів і обернено пропорційна відстані між ними. \[F=k_{C} \frac{q_{1} q_{2}}{r^{2}}\]У цій формулі\(k_{C} \approx 8.988 \times 10^{9} \mathrm{Nm}^{2} / \mathrm{C}^{2}\) і називається електростатична постійна. Змінні q1 та q2 представляють заряди (у Кулоні) на частинках (які можуть бути або додатними, або від'ємними числами), а r - відстань (у метрах) між зарядами. Нарешті, F являє собою силу заряду, виміряну в Ньютонах.
i Розв'яжіть формулу (3) для r.
II. За умови сили\(F=2.0 \times 10^{12} \mathrm{N}\), двох рівних зарядів\(q_{1}=q_{2}=1 \mathrm{C}\), знайти приблизну відстань між двома зарядженими частинками.
- Відповідь
-
Перехресний множимо, потім ділимо на коефіцієнт r.
\[\begin{aligned} F &=k_{C} \frac{q_{1} q_{2}}{r^{2}} \\ F r^{2} &=k_{C} q_{1} q_{2} \\ r^{2} &=\frac{k_{C} q_{1} q_{2}}{F} \end{aligned}\]
Нарешті, щоб знайти r, візьміть квадратний корінь.
\[r=\sqrt{\frac{k_{C} q_{1} q_{2}}{F}}\]
Щоб знайти відстань між зарядженими частинками, підставляють\(k_{C}=8.988 \times 10^{9} \mathrm{Nm}^{2} / \mathrm{C}^{2}\),
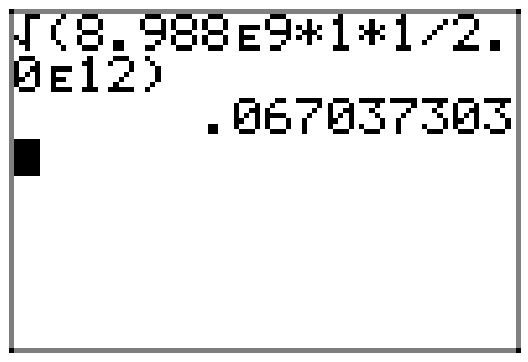
\(q_{1}=q_{2}=1 \mathrm{C},\) і\(F=2.0 \times 10^{12} \mathrm{N}\).\[r=\sqrt{\frac{\left(8.988 \times 10^{9}\right)(1)(1)}{2.0 \times 10^{12}}}\]
Калькулятор виробляє наближення,\(r \approx 0.067\) метри.
Виконуйте кожне з наступних завдань у Вправи\(\PageIndex{96}\) -\(\PageIndex{99}\).
i. Випишіть словами значення символів, які написані в позначеннях set-builder.
II. Напишіть деякі елементи цього набору.
iii. Намалюйте реальну лінію і намалюйте деякі точки, які знаходяться в цьому наборі.
Вправа\(\PageIndex{96}\)
\(A=\{x \in \mathbb{N} : x>10\}\)
- Відповідь
-
i. a - множина всіх\(x\) натуральних чисел, таких,\(x\) що більше\(10.\)
II. \(A=\{11,12,13,14, \ldots\}\)
iii.

Вправа\(\PageIndex{97}\)
\(B=\{x \in \mathbb{N} : x \geq 10\}\)
Вправа\(\PageIndex{98}\)
\(C=\{x \in \mathbb{Z} : x \leq 2\}\)
- Відповідь
-
i. c - множина всіх\(x\) в цілих чисел, таких, що\(x\) менше або дорівнює\(2.\)
II. \(C=\{\ldots,-4,-3,-2,-1,0,1,2\}\)
iii.

Вправа\(\PageIndex{99}\)
\(D=\{x \in \mathbb{Z} : x>-3\}\)
У Вправи\(\PageIndex{100}\) -\(\PageIndex{103}\) використовуйте набори A, B, C і D, які були визначені в Вправи\(\PageIndex{96}\) -\(\PageIndex{99}\). Опишіть наступні множини, використовуючи множинні позначення, і намалюйте відповідну діаграму Венна.
Вправа\(\PageIndex{100}\)
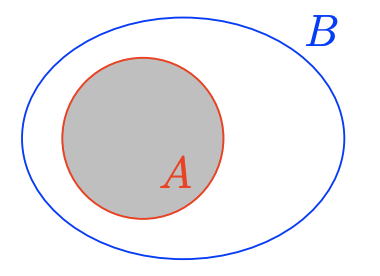
\(A \cap B\)
- Відповідь
-
\(A \cap B=\{x \in \mathbb{N} : x>10\}=\{11,12,13, \ldots\}\)
Вправа\(\PageIndex{101}\)
\(A \cup B\)
Вправа\(\PageIndex{102}\)
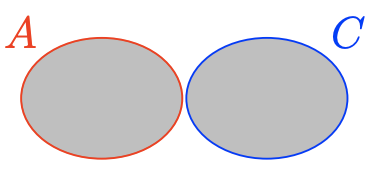
\(A \cup C\)
- Відповідь
-
\(A \cup C=\{x \in \mathbb{Z} : x \leq 2 \text { or } x>10\}=\{\ldots,-3,-2-1,0,1,2,11,12,13 \dots\}\)
Вправа\(\PageIndex{103}\)
\(C \cap D\)
У Вправи\(\PageIndex{104}\) - використовуйте як інтервальні\(\PageIndex{111}\), так і встановлені позначення для опису інтервалу, показаного на графіку.
Вправа\(\PageIndex{104}\)

- Відповідь
-
Заповнена окружність в кінцевій точці 3 вказує на те, що ця точка включена в множину. Таким чином, множина в інтервалі позначення є\([3, \infty)\), а в множині позначення\(\{x : x \geq 3\}\).
Вправа\(\PageIndex{105}\)

Вправа\(\PageIndex{106}\)

- Відповідь
-
Порожнє коло у кінцевій точці −7 вказує на те, що ця точка не включена до множини. Таким чином, множина в інтервалі позначення є\((-\infty,-7)\), а в множині -\(\{x : x<-7\}\).
Вправа\(\PageIndex{107}\)

Вправа\(\PageIndex{108}\)

- Відповідь
-
Порожнє коло в кінцевій точці 0 вказує, що ця точка не включена до множини. Таким чином, множина в інтервалі позначення є\((0, \infty)\), а в множині -\(\{x : x>0\}\).
Вправа\(\PageIndex{109}\)

Вправа\(\PageIndex{110}\)

- Відповідь
-
Порожнє коло у кінцевій точці −8 вказує на те, що ця точка не включена до множини. Таким чином, множина в інтервалі позначення є\((-8, \infty)\), а в множині -\(\{x : x>-8\}\).
Вправа\(\PageIndex{111}\)

У Вправи\(\PageIndex{112}\) -\(\PageIndex{119}\) накидайте графік заданого інтервалу.
Вправа\(\PageIndex{112}\)
\([2,5)\)
- Відповідь
-

Вправа\(\PageIndex{113}\)
\((-3,1]\)
Вправа\(\PageIndex{114}\)
\([1, \infty)\)
- Відповідь
-

Вправа\(\PageIndex{115}\)
\((-\infty, 2)\)
Вправа\(\PageIndex{116}\)
\(\{x :-4<x<1\}\)
- Відповідь
-

Вправа\(\PageIndex{117}\)
\(\{x : 1 \leq x \leq 5\}\)
Вправа\(\PageIndex{118}\)
\(\{x : x<-2\}\)
- Відповідь
-

Вправа\(\PageIndex{119}\)
\(\{x : x \geq-1\}\)
У Вправи\(\PageIndex{120}\) - використовуйте як інтервальні\(\PageIndex{127}\), так і встановлені позначення для опису перетину двох інтервалів, показаних на графіку. Також накидайте графік перетину на дійсній числовій лінії.
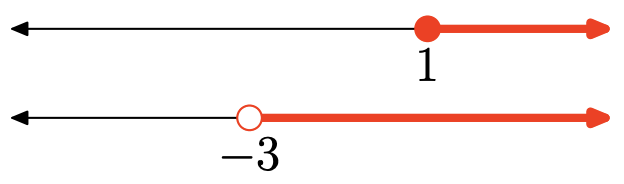
Вправа\(\PageIndex{120}\)
- Відповідь
-
Перетин - це сукупність точок, які знаходяться в обох інтервалах (затінених на обох графіках). Графік перетину:

\([1, \infty)=\{x : x \geq 1\}\)
Вправа\(\PageIndex{121}\)
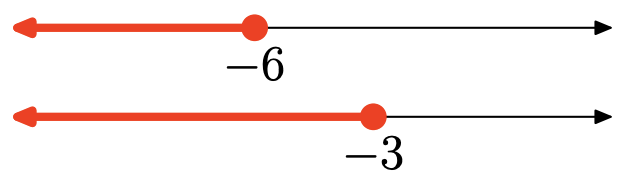
Вправа\(\PageIndex{122}\)
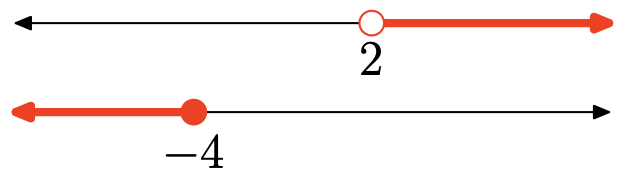
- Відповідь
-
Немає точок, які знаходяться в обох інтервалах (затінених в обох), тому немає перетину. Графік перетину:

немає перехрестя
Вправа\(\PageIndex{123}\)
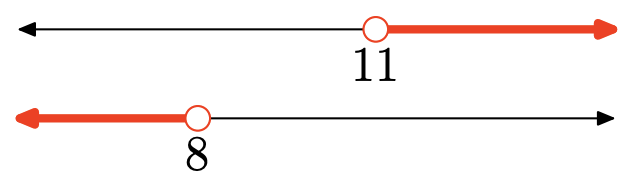
Вправа\(\PageIndex{124}\)
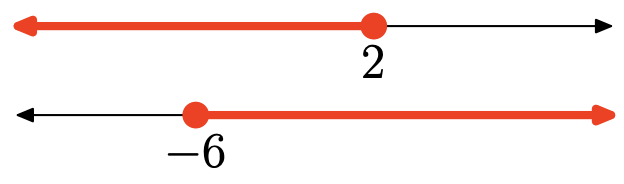
- Відповідь
-
Перетин - це сукупність точок, які знаходяться в обох інтервалах (затінених в обох). Графік перетину:

\([-6,2]=\{x :-6 \leq x \leq 2\}\)
Вправа\(\PageIndex{125}\)

Вправа\(\PageIndex{126}\)
- Відповідь
-
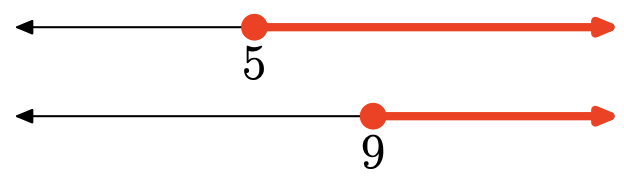
Перетин - це сукупність точок, які знаходяться в обох інтервалах (затінених в обох). Графік перетину:

\([9, \infty)=\{x : x \geq 9\}\)
Вправа\(\PageIndex{127}\)
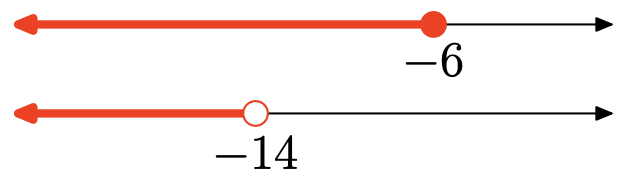
У Вправи\(\PageIndex{128}\) - використовуйте як інтервальні\(\PageIndex{135}\), так і встановлені позначення для опису об'єднання двох інтервалів, показаних на графіку. Також накидайте графік об'єднання на дійсній числовій лінії.
Вправа\(\PageIndex{128}\)
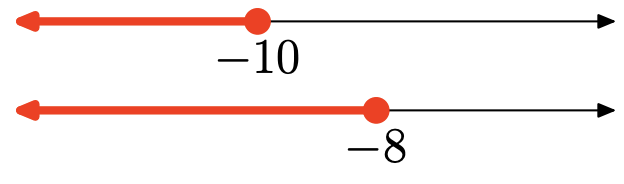
- Відповідь
-
Об'єднання - це множина всіх точок, які знаходяться в одному або іншому інтервалі (затінені в будь-якому графіку). Графік об'єднання:

\((-\infty,-8]=\{x : x \leq-8\}\)
Вправа\(\PageIndex{129}\)

Вправа\(\PageIndex{130}\)
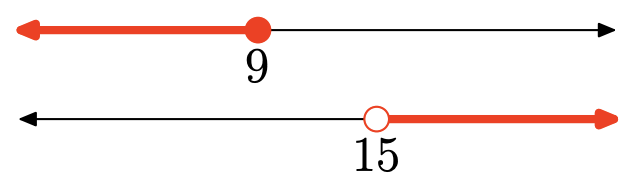
- Відповідь
-
Об'єднання - це множина всіх точок, які знаходяться в одному або іншому інтервалі (затінені в будь-якому графіку). Графік об'єднання:

\((-\infty, 9] \cup(15, \infty)\)
\(=\{x : x \leq 9 \text { or } x>15\}\)
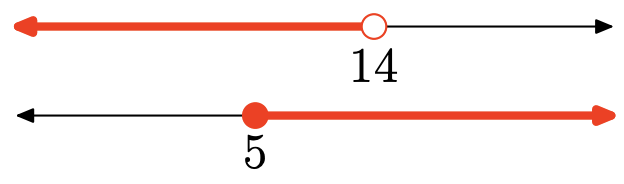
Вправа\(\PageIndex{131}\)
Вправа\(\PageIndex{132}\)
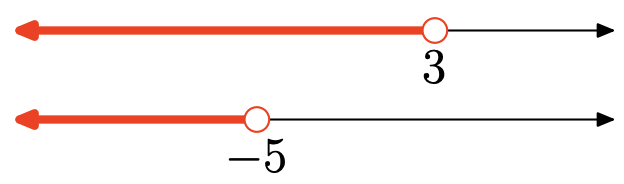
- Відповідь
-
Об'єднання - це сукупність всіх точок, які знаходяться в одному або іншому інтервалі (затінені в будь-якому). Графік об'єднання:

\((-\infty, 3)=\{x : x<3\}\)
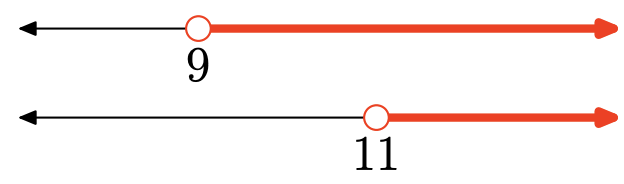
Вправа\(\PageIndex{133}\)
Вправа\(\PageIndex{134}\)
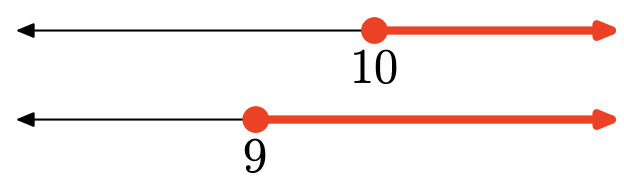
- Відповідь
-
Об'єднання - це сукупність всіх точок, які знаходяться в одному або іншому інтервалі (затінені в будь-якому). Графік об'єднання:

\([9, \infty)=\{x : x \geq 9\}\)
Вправа\(\PageIndex{135}\)
У Вправи\(\PageIndex{136}\) -56 використовуйте інтервальні позначення для опису заданого множини. Також накидайте графік множини на дійсній числовій лінії.
Вправа\(\PageIndex{136}\)
\(\{x : x \geq-6 \text { and } x>-5\}\)
- Відповідь
-
Цей набір такий же\(\{x : x>-5\}\), як, який знаходиться\((-5, \infty)\) в інтервальному позначенні. Графік набору:

Вправа\(\PageIndex{137}\)
\(\{x : x \leq 6 \text { and } x \geq 4\}\)
Вправа\(\PageIndex{138}\)
\(\{x : x \geq-1 \text { or } x<3\}\)
- Відповідь
-
Кожне дійсне число знаходиться в одному або іншому з двох інтервалів. Тому множина - це сукупність всіх дійсних чисел\((-\infty, \infty)\). Графік набору:

Вправа\(\PageIndex{139}\)
\(\{x : x>-7 \text { and } x>-4\}\)
Вправа\(\PageIndex{140}\)
\(\{x : x \geq -1 \text { or } x>6\}\)
- Відповідь
-
Цей набір такий же\(\{x : x \geq-1\}\), як, який знаходиться\([-1, \infty)\) в інтервальному позначенні. Графік набору:

Вправа\(\PageIndex{141}\)
\(\{x : x \geq 7 \text { or } x<-2\}\)
Вправа\(\PageIndex{142}\)
\(\{x : x \geq 6 \text { or } x>-3\}\)
- Відповідь
-
Цей набір такий же\(\{x : x>-3\}\), як, який знаходиться\((-3, \infty)\) в інтервальному позначенні. Графік набору:

Вправа\(\PageIndex{143}\)
\(\{x : x \leq 1 \text { or } x>0\}\)
Вправа\(\PageIndex{144}\)
\(\{x : x<2 \text { and } x<-7\}\)
- Відповідь
-
Цей набір такий же\(\{x : x<-7\}\), як, який знаходиться\((-\infty,-7)\) в інтервальному позначенні. Графік набору:

Вправа\(\PageIndex{145}\)
\(\{x : x \leq-3 \text { and } x<-5\}\)
Вправа\(\PageIndex{146}\)
\(\{x : x \leq-3 \text { or } x \geq 4\}\)
- Відповідь
-
Цей набір є об'єднанням двох інтервалів,\((-\infty,-3] \cup[4, \infty)\). Графік набору:

Вправа\(\PageIndex{147}\)
\(\{x : x<11 \text { or } x \leq 8\}\)
Вправа\(\PageIndex{148}\)
\(\{x : x \geq 5 \text { and } x \leq 1\}\)
- Відповідь
-
Немає чисел, які задовольняють обидві нерівності. Таким чином, перехрестя немає. Графік набору:

Вправа\(\PageIndex{149}\)
\(\{x : x<5 \text { or } x<10\}\)
Вправа\(\PageIndex{150}\)
\(\{x : x \leq 5 \text { and } x \geq-1\}\)
- Відповідь
-
Ця множина є такою ж\(\{x :-1 \leq x \leq 5\}\), яка є [−1, 5] у інтервальній нотації. Графік множини

Вправа\(\PageIndex{151}\)
\(\{x : x>-3 \text { and } x<-6\}\)
У Вправи\(\PageIndex{152}\) -\(\PageIndex{163}\) вирішуйте нерівність. Висловлюйте свою відповідь в обох інтервалах і встановлених позначеннях і затіньте рішення на числовому рядку.
Вправа\(\PageIndex{152}\)
\(-8 x-3 \leq-16 x-1\)
- Відповідь
-
\[\begin{aligned} & -8 x-3 \leq-16 x-1 \\ \Longrightarrow \quad & − 8x + 16x \leq −1 + 3 \\ \Longrightarrow \quad& 8x \leq 2 \\ \Longrightarrow \quad & x \leq \frac{1}{4}\end{aligned}\]
Таким чином, інтервал розв'язку дорівнює\((−\infty, \frac{1}{4}]\) =\(\{x|x \leq \frac{1}{4}\}\).

Вправа\(\PageIndex{153}\)
\(6 x-6>3 x+3\)
Вправа\(\PageIndex{154}\)
\(-12 x+5 \leq-3 x-4\)
- Відповідь
-
\[\begin{aligned} & -12 x+5 \leq-3 x-4 \\ \Longrightarrow \quad & -12x + 3x \leq −4 − 5 \\ \Longrightarrow \quad& -9x \leq -9 \\ \Longrightarrow \quad & x \geq 1\end{aligned}\]
Таким чином, інтервал розчину становить\([1,\infty) = \{x|x \geq 1\}\).

Вправа\(\PageIndex{155}\)
\(7 x+3 \leq-2 x-8\)
Вправа\(\PageIndex{156}\)
\(-11 x-9<-3 x+1\)
- Відповідь
-
\[\begin{aligned} & − 11x − 9 < −3x + 1 \\ \Longrightarrow \quad & − 11x + 3x < 1 + 9 \\ \Longrightarrow \quad& − 8x < 10 \\ \Longrightarrow \quad & x > -\frac{5}{4}\end{aligned}\]
Таким чином, інтервал розчину становить\((−\frac{5}{4} ,\infty) = \{x|x >−\frac{5}{4} \}\).
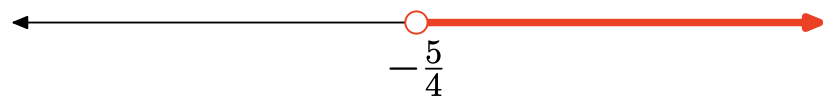
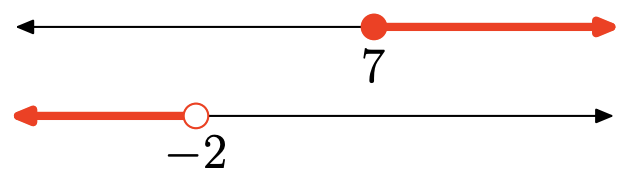
Вправа\(\PageIndex{157}\)
\(4 x-8 \geq-4 x-5\)
Вправа\(\PageIndex{158}\)
\(4 x-5>5 x-7\)
- Відповідь
-
\[\begin{aligned} & 4x − 5 > 5x − 7\\ \Longrightarrow \quad & 4x − 5x > −7 + 5 \\ \Longrightarrow \quad& − x > −2 \\ \Longrightarrow \quad &x < 2\end{aligned}\]
Таким чином, інтервал розчину становить\((−\infty, 2) = \{x|x < 2\}\).
Вправа\(\PageIndex{159}\)
\(-14 x+4>-6 x+8\)
Вправа\(\PageIndex{160}\)
\(2 x-1>7 x+2\)
- Відповідь
-
\[\begin{aligned} & 2x − 1 > 7x + 2\\ \Longrightarrow \quad & 2x − 7x > 2 + 1 \\ \Longrightarrow \quad& − 5x > 3 \\ \Longrightarrow \quad &x < −\frac{3}{5}\end{aligned}\]
Таким чином, інтервал розчину становить\((−\infty, −\frac{3}{5}) = \{x|x < −\frac{3}{5}\}\).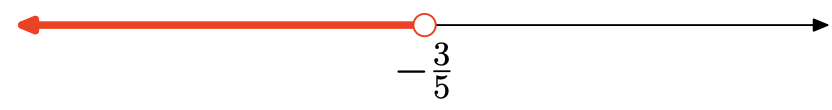
Вправа\(\PageIndex{161}\)
\(-3 x-2>-4 x-9\)
Вправа\(\PageIndex{162}\)
\(-3 x+3<-11 x-3\)
- Відповідь
-
\[\begin{aligned} & − 3x + 3 < −11x − 3\\ \Longrightarrow \quad & − 3x + 11x < −3 − 3 \\ \Longrightarrow \quad& 8x < −6 \\ \Longrightarrow \quad &x < -\frac{3}{4}\end{aligned}\]
Таким чином, інтервал розчину становить\((−\infty, −\frac{3}{4}) = \{x|x < −\frac{3}{4}\}\).
Вправа\(\PageIndex{163}\)
\(6 x+3<8 x+8\)
У вправах 13-50 розв'яжіть складну нерівність. Висловлюйте свою відповідь в обох інтервалах і встановлених позначеннях і затіньте рішення на числовому рядку.
Вправа\(\PageIndex{164}\)
\(2 x-1<4\)або\(7 x+1 \geq-4\)
- Відповідь
-
\[\begin{aligned} & 2x − 1 < 4 \text{ or } 7x + 1 \geq −4\\ \Longrightarrow \quad & 2x < 5\quad \text{or}\quad 7x \geq −5 \\ \Longrightarrow \quad&x<\frac{5}{2}\quad\text{or}\quad x\geq-\frac{5}{7}\end{aligned}\]

Для об'єднання затінюйте все, що затінено в будь-якому графіку. Рішення - множина всіх дійсних чисел\((−\infty,\infty)\).

Вправа\(\PageIndex{165}\)
\(-8 x+9<-3\)і\(-7 x+1>3\)
Вправа\(\PageIndex{166}\)
\(-6 x-4<-4\)і\(-3 x+7 \geq-5\)
- Відповідь
-
\[\begin{aligned} & − 6x − 4 < −4 \text{ and } − 3x + 7 \geq −5\\ \Longrightarrow \quad & -6x < 0\quad \text{and}\quad -3x \geq −12 \\ \Longrightarrow \quad&x>0\quad\text{and}\quad x\leq4 \\ \Longrightarrow \quad & 0< x \leq 4 \end{aligned}\]
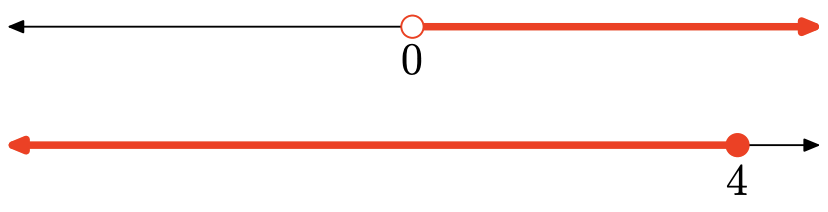
Перетин - це всі точки, затінені на обох графіках, тому рішення є\((0, 4] = \{x|0 < x \leq 4\}\).

Вправа\(\PageIndex{167}\)
\(-3 x+3 \leq 8\)і\(-3 x-6>-6\)
Вправа\(\PageIndex{168}\)
\(8 x+5 \leq-1\)і\(4 x-2>-1\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{169}\)
\(-x-1<7\)і\(-6 x-9 \geq 8\)
Вправа\(\PageIndex{170}\)
\(-3 x+8 \leq-5\)або\(-2 x-4 \geq-3\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{171}\)
\(-6 x-7<-3\)і\(-8 x \geq 3\)
Вправа\(\PageIndex{172}\)
\(9 x-9 \leq 9\)і\(5 x>-1\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-7 x+3<-3\)або\(-8 x \geq 2\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(3 x-5<4\)і\(-x+9>3\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-8 x-6<5\)або\(4 x-1 \geq 3\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(9 x+3 \leq-5\)або\(-2 x-4 \geq 9\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-7 x+6<-4\)або\(-7 x-5>7\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(4 x-2 \leq 2\)або\(3 x-9 \geq 3\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-5 x+5<-4\)або\(-5 x-5 \geq-5\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(5 x+1<-6\)і\(3 x+9>-4\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(7 x+2<-5\)або\(6 x-9 \geq-7\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-7 x-7<-2\)і\(3 x \geq 3\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(4 x+1<0\)або\(8 x+6>9\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(7 x+8<-3\)і\(8 x+3 \geq-9\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(3 x<2\)і\(-7 x-8 \geq 3\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-5 x+2 \leq-2\)і\(-6 x+2 \geq 3\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(4 x-1 \leq 8\)або\(3 x-9>0\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(2 x-5 \leq 1\)і\(4 x+7>7\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(3 x+1<0\)або\(5 x+5>-8\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-8 x+7 \leq 9\)або\(-5 x+6>-2\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(x-6 \leq-5\)і\(6 x-2>-3\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-4 x-8<4\)або\(-4 x+2>3\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(9 x-5<2\)або\(-8 x-5 \geq-6\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-9 x-5 \leq-3\)або\(x+1>3\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-5 x-3 \leq 6\)і\(2 x-1 \geq 6\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-1 \leq-7 x-3 \leq 2\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(0<5 x-5<9\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(5<9 x-3 \leq 6\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-6<7 x+3 \leq 2\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-2<-7 x+6<6\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-9<-2 x+5 \leq 1\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
У вправах 51-62 розв'яжіть задану нерівність для x. Графік розв'язку, встановленого на числовому рядку, а потім використовуйте інтервал і множинні позначення для опису множини розв'язків.
Вправа\(\PageIndex{1}\)
\(-\frac{1}{3}<\frac{x}{2}+\frac{1}{4}<\frac{1}{3}\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-\frac{1}{5}<\frac{x}{2}-\frac{1}{4}<\frac{1}{5}\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-\frac{1}{2}<\frac{1}{3}-\frac{x}{2}<\frac{1}{2}\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-\frac{2}{3} \leq \frac{1}{2}-\frac{x}{5} \leq \frac{2}{3}\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-1<x-\frac{x+1}{5}<2\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-2<x-\frac{2 x-1}{3}<4\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-2<\frac{x+1}{2}-\frac{x+1}{3} \leq 2\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-3<\frac{x-1}{3}-\frac{2 x-1}{5} \leq 2\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(x<4-x<5\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-x<2 x+3 \leq 7\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(-x<x+5 \leq 11\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
\(−2x < 3 − x \leq 8\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Аерон влаштував демонстрацію «Як зробити комету» професора О'Коммеля. Мудрий професор попросив Аерон переконатися, що аудиторія залишається між 15 і 20 градусами Цельсія (C). Aeron знає, що термостат знаходиться в Фаренгейті (F), і він також знає, що формула перетворення між двома температурними шкалами становить C = (5/9) (F − 32).
а) Налаштовуючи складну нерівність для запитуваного температурного діапазону в Цельсії, отримаємо\(15 \leq C \leq 20\). Використовуючи наведену вище формулу перетворення, встановіть відповідну складну нерівність у Фаренгейті.
б) Розв'яжіть складну нерівність у частині (а) для F. Напишіть свою відповідь у множинних позначеннях.
в) Які можливі температури (лише цілі числа), які Aeron може встановити термостат у Фаренгейті?
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Вправа\(\PageIndex{1}\)
Додайте сюди текст вправ.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.