1.4: Дроби

Цілі навчання

• Зменшіть частку до найнижчих показників.
• Множення і ділення дробів.
• Додавання і віднімання дробів.

Зменшення

Дріб - це дійсне число, записане у вигляді частки, або співвідношення, двох цілих чисел\(a\) and\(b\), де\(b \neq 0\).

Малюнок\(\PageIndex{1}\)

Ціле число над рядком дробу називається чисельником, а ціле число нижче називається знаменником. Чисельник часто називають «частиною», а знаменник часто називають «цілим». Еквівалентні дроби - це два рівних співвідношення, виражені за допомогою різних чисельників і знаменників. Наприклад,

\(\frac{50}{100} = \frac{1}{2}\)

П'ятдесят частин з\(100\) - це те саме співвідношення, що\(2\) і\(1\) частина з і являє собою те саме дійсне число. Розглянемо наступні факторизації\(50\) і\(100\):

\ [
\ почати {вирівнювати*}
50 &= 2\ cdot 25\\
100 &= 4\ cdot 25
\ кінець {вирівнювати*}
\]

Цифри\(50\) і\(100\) поділяють коефіцієнт\(25\). Спільний фактор називається загальним фактором. Ми можемо переписати співвідношення\(\frac{50}{100}\) наступним чином:

\(\frac{50}{100} = \frac{2 \cdot 25}{4 \cdot 25}\)

Використовуючи мультиплікативну властивість ідентичності та той факт\(\frac{25}{25} = 1\), що ми маємо

Малюнок\(\PageIndex{2}\)

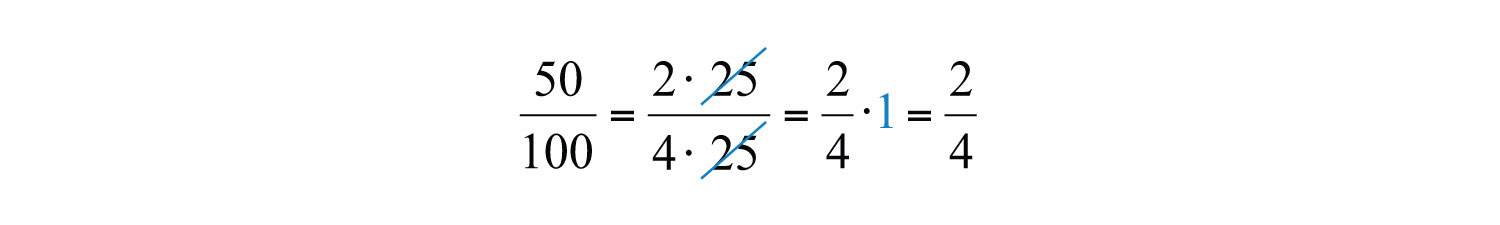
Поділ\(\frac{25}{25}\) і заміна цього фактора на а\(1\) називається скасуванням. Разом ці основні етапи знаходження еквівалентних дробів визначають процес скорочення. Так як множники поділяють свій твір рівномірно, ми досягаємо однакового результату, діливши і чисельник, і знаменник на\(25\) наступне:

Малюнок\(\PageIndex{3}\)

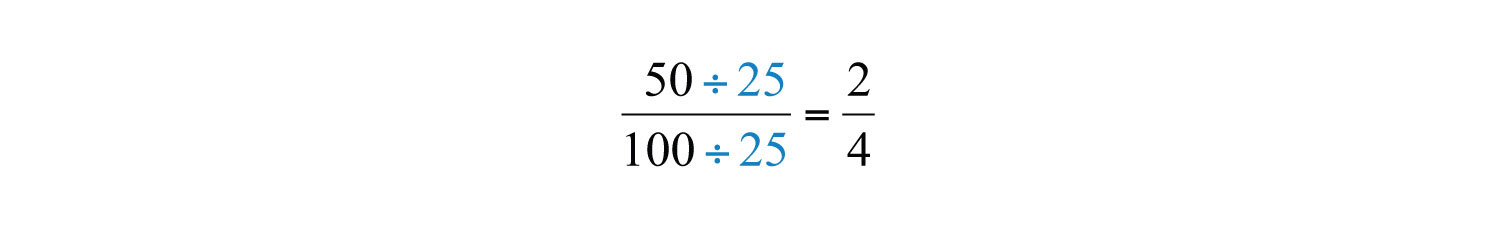
Знаходження еквівалентних дробів, де чисельник і знаменник не мають спільного множника, крім\(1\) називається скороченням до найнижчих чисел. Навчаючись, як звести до найнижчих термінів, корисно спочатку переписати чисельник і знаменник як добуток простих чисел, а потім скасувати. Наприклад,

Малюнок\(\PageIndex{4}\)

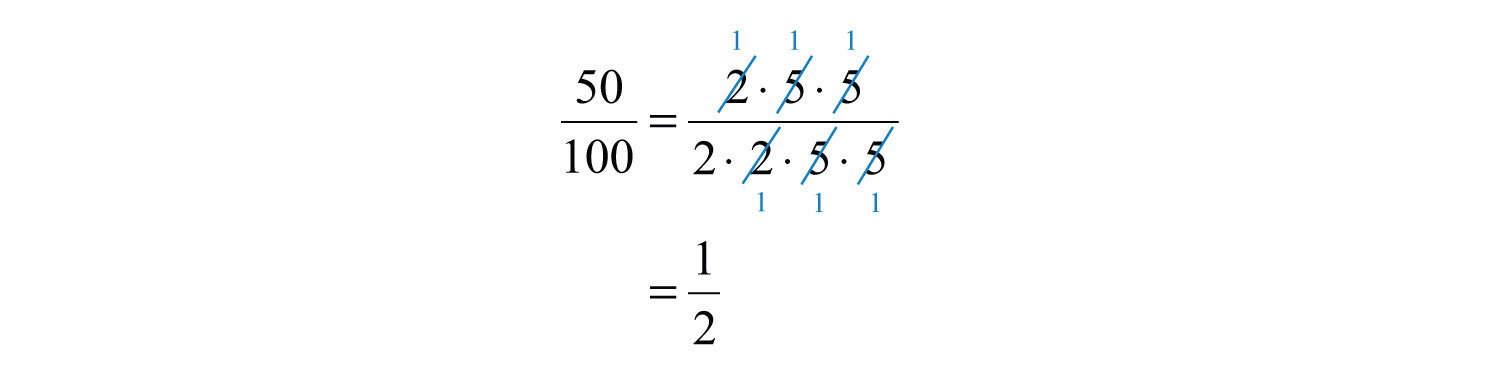
Такого ж результату досягаємо, діливши чисельник і знаменник на найбільший спільний коефіцієнт (ГКФ). GCF - це найбільше число, яке ділить і чисельник, і знаменник рівномірно. Один із способів знайти GCF\(50\) і\(100\) полягає в тому, щоб перерахувати всі фактори кожного і визначити найбільшу кількість, яка з'являється в обох списках. Пам'ятайте, кожне число також є фактором самого себе.

\ [
\ почати {вирівнювати*}
&\ {1,2,5,10,25,50\} &&\ колір {Кольоровий} {Фактори\ з\ 50}\\
&\ {1,2,4,5,10,20,25,50,100\} &\ колір {Кольоровий} {Фактори\ з\ 100}
\ кінець {вирівнювати*}
\]

Загальні фактори перераховані жирним шрифтом, і ми бачимо, що найбільшим загальним фактором є\(50\). Використовуємо наступні позначення для позначення GCF двох чисел: GCF\((50, 100) = 50\). Після визначення ГКФ зменшіть, діливши і чисельник, і знаменник наступним чином:

Малюнок\(\PageIndex{5}\)

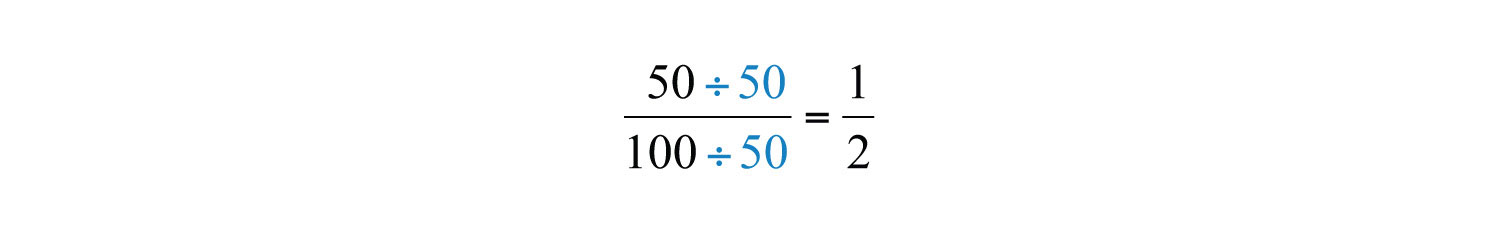
Приклад\(\PageIndex{1}\)

Знизити до найнижчих термінів:\(\frac{105}{300}\).

Рішення

Перепишіть чисельник і знаменник як добуток простих чисел, а потім скасуйте.

Малюнок\(\PageIndex{6}\)

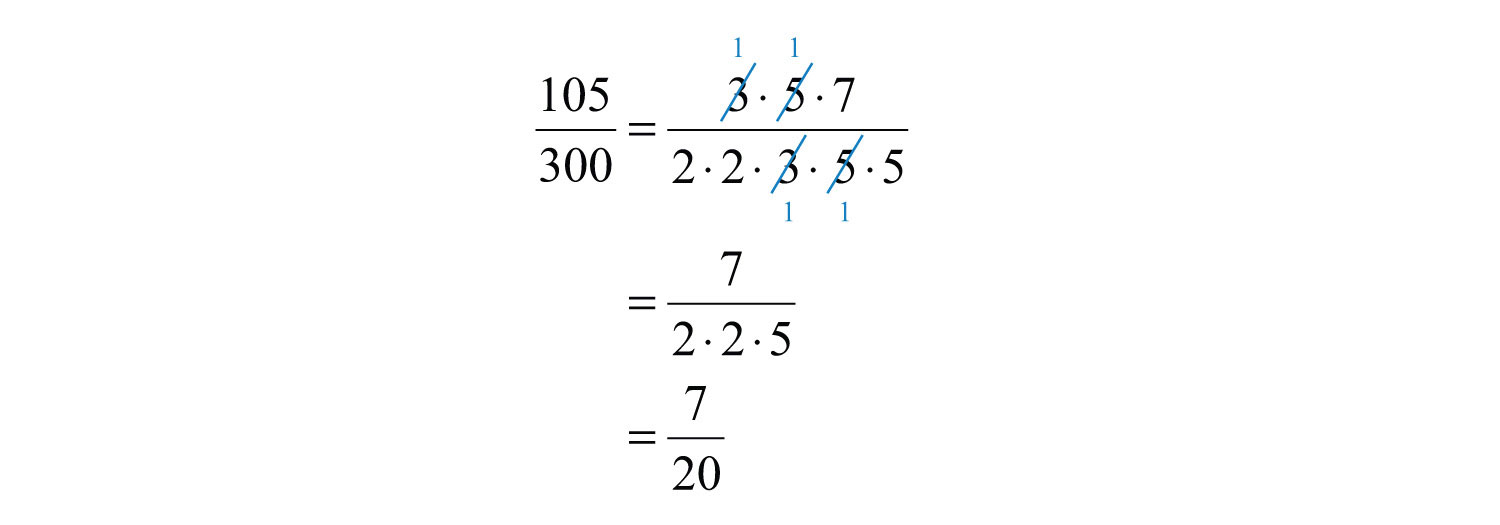
Як варіант, ми досягаємо того ж результату, якщо розділимо і чисельник, і знаменник на ЗКФ\((105, 300)\). Швидкий спосіб знайти GCF двох чисел вимагає від нас спочатку написати кожне як добуток простих чисел. GCF є добутком всіх загальних простих множників.

Малюнок\(\PageIndex{7}\)

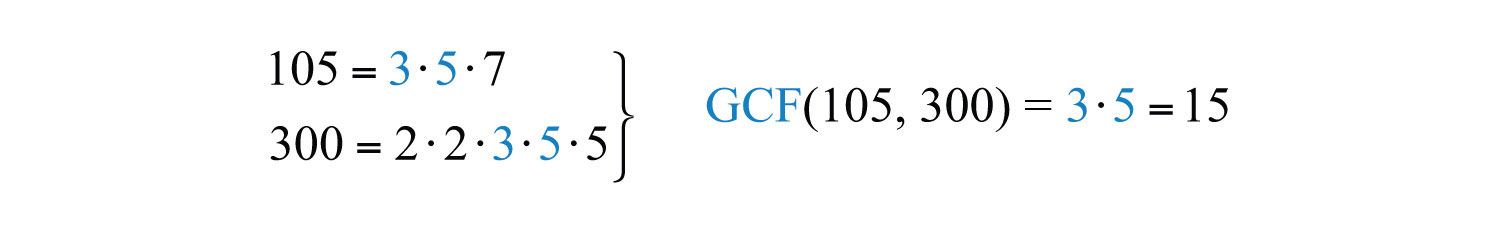
При цьому загальні прості множники є\(3\) і\(5\) і найбільшим загальним фактором\(105\) і\(300\) є\(15\).

Малюнок\(\PageIndex{8}\)

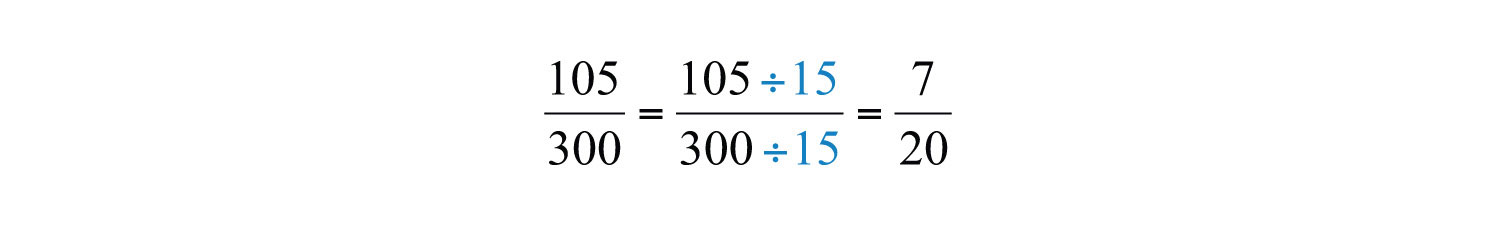
Відповідь:

\(\frac{7}{20}\)

Приклад\(\PageIndex{2}\)

Спробуйте це! Знизити до найнижчих термінів:\(\frac{32}{96}\).

Відео Рішення:

(натисніть, щоб подивитися відео)

Неправильний дріб - це той, де чисельник більше знаменника. Мішане число - це число, яке представляє суму цілого числа і дробу. Наприклад,\(5 \frac{1}{2}\) це мішане число, яке представляє суму\(5+\frac{1}{2}\). Використовуйте довге ділення для перетворення неправильного дробу в мішане число; залишок - чисельник дробової частини.

Приклад\(\PageIndex{3}\)

Пишіть\(\frac{23}{5}\) як мішане число.

Рішення

Зверніть увагу, що\(5\) ділиться на\(23\) чотири рази з залишком\(3\).

Малюнок\(\PageIndex{9}\)

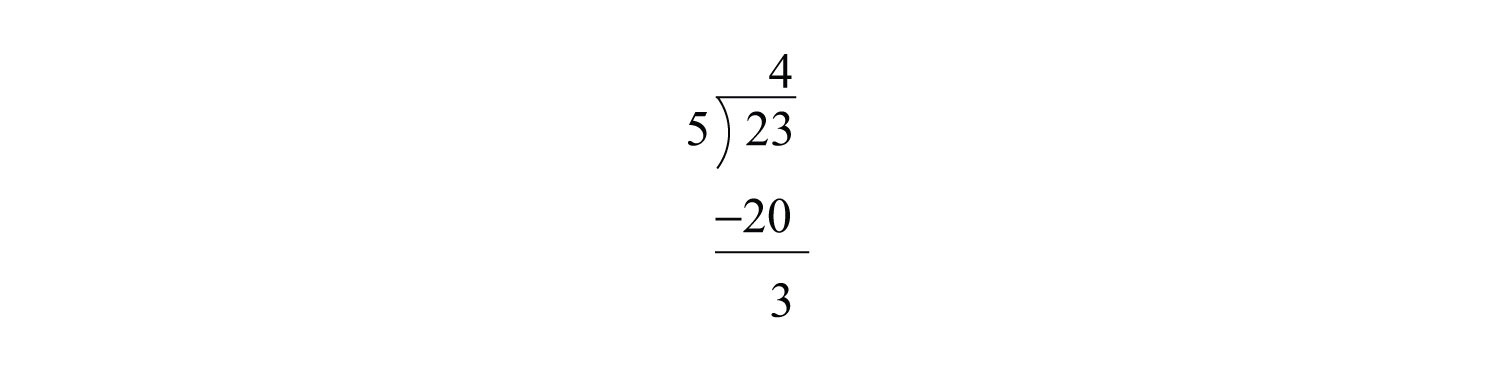
Тоді ми можемо написати

\ [
\ почати {вирівнювати*}
\ гідророзриву {23} {5} &= 4 +\ гідророзриву {3} {5}\
&= 4\ гідророзриву {3} {5}
\ end {align*}
\]

Зверніть увагу, що знаменник дробової частини змішаного числа залишається таким же, як і знаменник вихідного дробу.

Відповідь

\(4 \frac{3}{5}\)

Щоб перетворити мішані числа на неправильні дроби, помножте ціле число на знаменник, а потім додайте чисельник; запишіть цей результат поверх початкового знаменника.

Приклад\(\PageIndex{4}\)

Пишіть\(3 \frac{5}{7}\) як неправильний дріб.

Рішення

Отримайте чисельник, множивши\(7\) раз,\(3\) а потім складіть\(5\).

\ [
\ почати {вирівнювати*}
3\ гідророзриву {5} {7} &=\ гідророзриву {7\ cdot 3 + 5} {7}\
&=\ гідророзриву {21+5} {7}\
&=\ frac {26} {7}
\ end {align*}
\\]

Відповідь

\(\frac{26}{7}\)

Важливо відзначити, що перетворення в мішане число не є частиною процесу скорочення. Ми вважаємо, що неправильні дроби\(267\), наприклад, зводяться до найнижчих. В алгебрі часто краще працювати з неправильними дробами, хоча в деяких додатках більш доречні мішані числа.

Приклад\(\PageIndex{5}\)

Спробуйте це! \(10 \frac{1}{2}\)Перетворити на неправильний дріб.

Рішення

(натисніть, щоб подивитися відео)

Множення та ділення дробів

У цьому розділі, припустимо\(a, b, c\), що, і\(d\) всі ненульові цілі числа. Твір двох дробів - це дріб, утворений добутком чисельників і добутком знаменників. Іншими словами, для множення дробів множимо чисельники і множимо знаменники:

\(\frac{a}{b} \cdot \frac{c}{d} = \frac{ac}{bd}\)

Приклад\(\PageIndex{6}\)

Помножити:\(\frac{2}{3} \cdot \frac{5}{7}\)

Рішення

Множимо чисельники і множимо знаменники.

\ [
\ почати {вирівнювати*}
\ гідророзриву {2} {3}\ cdot\ гідророзриву {5} {7} &=\ гідророзриву {2\ cdot 5} {3\ cdot 7}\\
&=\ frac {10} {21}
\ кінець {вирівнювати*}
\]

Відповідь:

\(\frac{10}{21}\)

Приклад\(\PageIndex{7}\)

Помножити:\(\frac{5}{9}\left(-\frac{1}{4}\right)\)

Рішення

Нагадаємо, що добуток позитивного числа і негативного числа є негативним.

\ [
\ почати {вирівнювати*}
\ гідророзриву {5} {9}\ ліворуч (-\ гідророзриву {1} {4}\ праворуч) &= -\ розриву {5\ cdot 1} {9\ cdot 4}\\
&= -\ frac {5} {36}
\ end {align*}
\]

Відповідь:

\(-\frac{5}{36}\)

Приклад\(\PageIndex{8}\)

Помножити:\(\frac{2}{3} \cdot 5 \frac{3}{4}\)

Рішення

Почніть\(5 \frac{3}{4}\) з перетворення в неправильний дріб.

Малюнок\(\PageIndex{10}\)

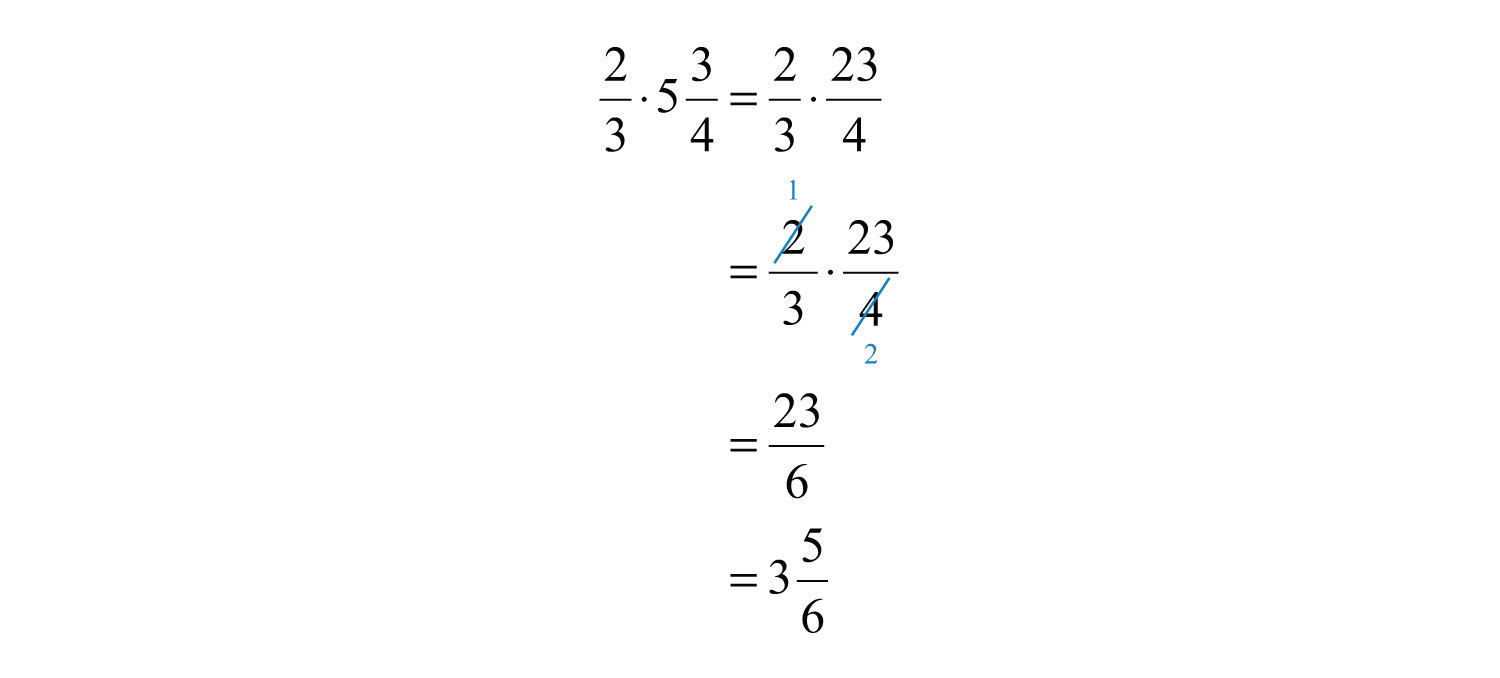
У цьому прикладі ми помітили, що ми могли б зменшити, перш ніж помножити чисельники і знаменники. Зменшення таким чином називається перехресним скасуванням, і може заощадити час при множенні дробів.

Відповідь

\(3 \frac{5}{6}\)

Два дійсних числа, твір\(1\) яких називається зворотними. Тому\(\frac{a}{b}\) і\(\frac{b}{a}\) є взаємними тому що\( \frac{a}{b} \cdot \frac{b}{a} = \frac{ab}{ab} = 1\). Наприклад,

\(\frac{2}{3} \cdot \frac{3}{2} = \frac{6}{6} = 1\)

Тому що їх продукт є\(1\),\(\frac{2}{3}\) і\(\frac{3}{2}\) є взаємними. Деякі інші взаємні перелічені нижче:

\(\frac{5}{8}\ \text{and}\ \frac{8}{5} \qquad 7\ \text{and}\ \frac{1}{7} \qquad -\frac{4}{5}\ \text{and}\ -\frac{5}{4}\)

Це визначення важливо, оскільки ділення дробів вимагає, щоб ви помножили дивіденд на зворотний дільник.

\(\frac{a}{b} \div \color{Cerulean}{\frac{c}{d}} \color{Black}{=} \frac{a}{b} \cdot \color{Cerulean}{\frac{d}{c}} \color{Black}{=} \frac{ad}{bc} \)

Приклад\(\PageIndex{9}\)

Розділити:\(\frac{2}{3} \div \frac{5}{7}\)

Рішення

\(\frac{2}{3}\)Помножте на зворотну\(\frac{5}{7}\).

\ [
\ почати {вирівнювати*}
\ гідророзриву {2} {3}\ div\ гідророзриву {5} {7} &=\ гідророзриву {2} {3}\ cdot\ гідророзриву {7} {5}\\ &=\ frac {2\ cdot 7} {3\ cdot 5}\\
&=\ гідророзриву {14} {15}\ кінець {2\ cdot 7} {3\ cdot 5}\\
&=\ гідророзриву {14} {15}
\ кінець {align*}
\\

Відповідь:

\(\frac{14}{15\)

Також потрібно знати про інші форми позначення, які вказують на поділ:/і —. Наприклад,

\(5/(1/2) = 5*(2/1)=(5/1)*(2/1)= 10/1=10\)

Або

\(\frac{\frac{7}{8}}{\color{Cerulean}{\frac{2}{3}}} \color{Black}{=} \frac{7}{8} \div \color{Cerulean}{\frac{2}{3}} \color{Black}{=} \frac{7}{8} \cdot \color{Cerulean}{\frac{3}{2}} \color{Black}{=} \frac{21}{16}\)

Останній є прикладом складного дробу, який представляє собою дріб, чисельник якого, знаменник або обидва є дробами.

Примітка

Студенти часто запитують, чому ділення еквівалентно множенню на зворотний дільника. Математичне пояснення походить від того, що добуток взаємних є\(1\). Якщо застосувати мультиплікативну властивість ідентичності і помножити чисельник і знаменник на зворотні знаменника, то отримаємо наступне:

Малюнок\(\PageIndex{11}\)

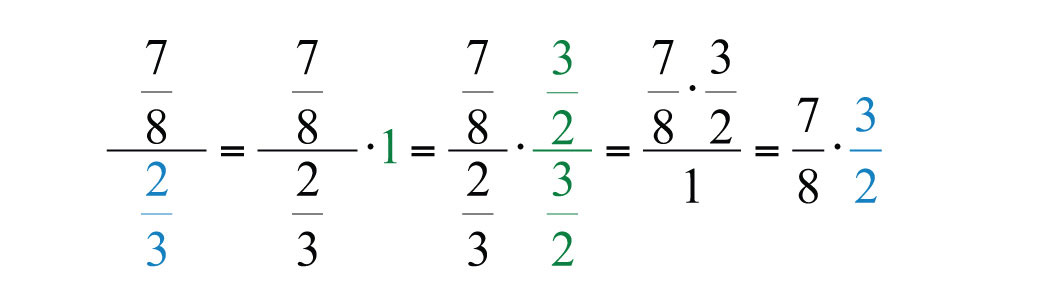
Перед множенням шукайте загальні фактори для скасування; це позбавляє від необхідності зменшення кінцевого результату.

Приклад\(\PageIndex{10}\)

Розділити:\(\frac{\frac{5}{2}}{\frac{7}{4}}\).

Рішення

Малюнок\(\PageIndex{12}\)

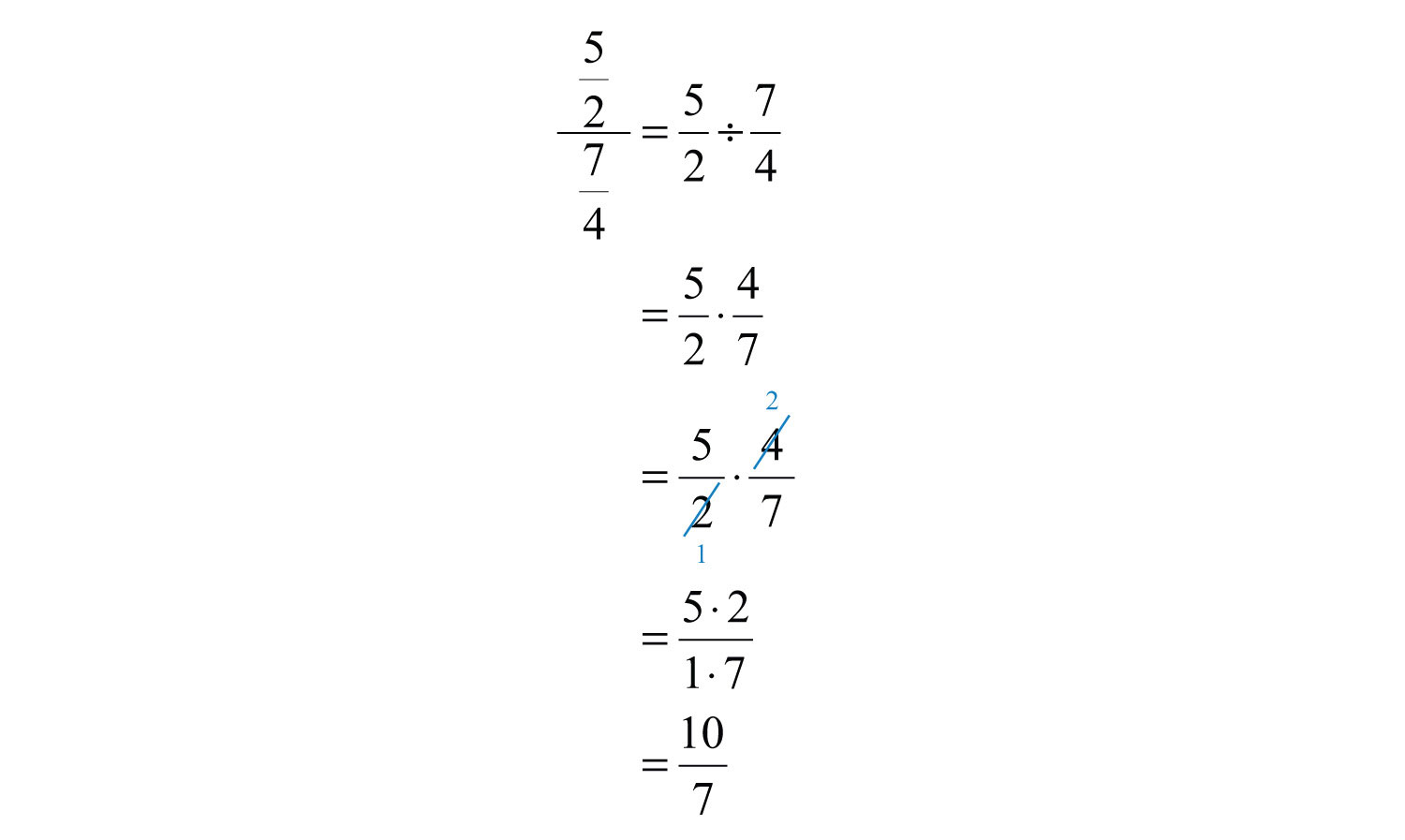
Відповідь

\(\frac{10}{7}\)

При діленні на ціле число корисно переписати його як дріб над\(1\).

Приклад\(\PageIndex{11}\)

Розділити:\(\frac{2}{3} \div 6\)

Рішення

Перепишіть 6 як\(\frac{6}{1}\) і помножте на його взаємні.

Малюнок\(\PageIndex{13}\)

Відповідь:

\(\frac{1}{9}\)

Також зверніть увагу, що ми скасовуємо тільки при роботі з множенням. Перепишіть будь-яку проблему поділу як продукт перед скасуванням.

Приклад\(\PageIndex{12}\)

Спробуйте це! Розділити:\(5 \div 2 \frac{3}{5} \)

Відео Рішення:

(натисніть, щоб подивитися відео)

Додавання та віднімання дробів

Негативні дроби позначаються негативним знаком перед рядком дробу, в чисельнику, або в знаменнику. Всі такі форми рівнозначні і взаємозамінні.

\(\frac{-3}{4} = -\frac{3}{4} = \frac{3}{-4}\)

Додавання або віднімання дробів вимагає спільного знаменника. У цьому розділі припустимо, що спільний знаменник c є ненульовим цілим числом.

Хорошою практикою є використання позитивних спільних знаменників шляхом вираження негативних дробів з негативними чисельниками. Коротше кажучи, уникайте негативних знаменників.

Приклад\(\PageIndex{13}\)

Відніміть:\(\frac{12}{15} - \frac{3}{15}\)

Рішення

Два дроби мають спільний знаменник\(15\). Тому відніміть чисельники і запишіть результат над спільним знаменником:

\ [
\ begin {align*}
\ frac {12} {15} -\ frac {3} {15} &=\ frac {12-3} {15} &&\ color {Cerulean} {Відніміть\ чисельники.} \\
&=\ колір {чорний} {\ розрив {9} {15}}\\
&=\ розрив {9\ колір {\ div 3}} {\ колір {чорний} {15}\ колір {Cerulean} {\ div 3}} &&\ колір {Cerulean} {Зменшити.} \\
&=\ гідророзриву {3} {5}
\ end {align*}
\]

Відповідь
\(\frac{3}{5}\)

Більшість проблем, з якими ви, ймовірно, зіткнетеся, матимуть на відміну від знаменників. У цьому випадку спочатку знайдіть еквівалентні дроби із загальним знаменником перед додаванням або відніманням чисельників. Одним із способів отримання еквівалентних дробів є поділ чисельника і знаменника на одне і те ж число. Зараз ми розглянемо методику знаходження еквівалентних дробів шляхом множення чисельника і знаменника на одне і те ж число. Повинно бути зрозуміло, що\(5/5\) дорівнює\(1\) і що\(1\) помножене на будь-яке число це число:

\(\frac{1}{2} = \frac{1}{2} \cdot \color{Cerulean}{1} \color{Black}{=} \frac{1}{2} \cdot \color{Cerulean}{\frac{5}{5}} \color{Black}{=} \frac{5}{10}\)

У нас є еквівалентні дроби\(\frac{1}{2}=\frac{5}{10}\). Скористайтеся цією ідеєю, щоб знайти еквівалентні дроби зі спільним знаменником для додавання або віднімання дробів. Кроки викладені в наступному прикладі.

Приклад\(\PageIndex{14}\)

Відніміть:\(\frac{7}{15} - \frac{3}{10}\)

Рішення

Крок 1: Визначте спільний знаменник. Для цього використовують найменше спільне кратне (НКМ) заданих знаменників. LCM\(15\) і\(10\) позначається LCM\((15, 10)\). Постарайтеся придумати найменшу цифру, на яку обидва знаменника поділяють рівномірно. Перерахуйте кратні кожному числу:

Загальні кратні перераховані жирним шрифтом, а найменш загальним кратним є\(30\).

LCM\((10,15)=30\)

Крок 2: Помножте чисельник і знаменник кожного дробу на значення, які призводять до отримання еквівалентних дробів з визначеним спільним знаменником.

\ [\ begin {align*}
\ frac {7} {15} -\ frac {3} {10} &=\ frac {7\ color {Cerulean} {\ cdot 2}} {15\ color {cdot 3}} -\ frac {3\ колір {\ cdot 3}} {10\ кольоровий {Cdot 3}\ cdot 3}}\\
&=\ гідророзриву {14} {30} -\ frac {9} {30}
\ end {align*}\]

Крок 3: Додайте або відніміть чисельники, запишіть результат над загальним знаменником, а потім зменшіть, якщо це можливо.

\ [\ почати {вирівнювати*}
\ гідророзриву {14} {30} -\ розрив {9} {30} &=\ гідророзриву {14-9} {30}\
&=\ гідророзриву {5} {30}\
&=\ фрак {5\ колір {\ div 5}} {30\ колір {\ div 5} {\ div 5} {\
div 5} гідророзрив {1} {6}
\ end {align*}\]

Відповідь:

\(\frac{1}{6}\)

Найменш поширеним кратним знаменників називається найменш спільний знаменник (РК). Пошук РК-дисплея часто є складним кроком. Це варто знайти, тому що якщо використовується будь-яке спільне множинне, крім найменшого, тоді буде задіяно більше кроків при зменшенні.

Приклад\(\PageIndex{15}\)

Додати:\(\frac{5}{10} + \frac{1}{18}\)

Рішення

Спочатку визначте, що LCM\((10, 18)\) є,\(90\) а потім знайдіть еквівалентні дроби з\(90\) як знаменник.

\ [\ почати {вирівнювати*}
\ frac {5} {10} +\ frac {1} {18} &=\ frac {5\ колір {Cerulean} {\ cdot 9}} {1\ колір {\ cdot 5}} {1\ колір {\ cdot 5}} {18\ колір {Croulean}\ cdot 5}}\\
&=\ гідророзриву {45} {90} +\ гідророзриву {5} {90}\
&=\ гідророзриву {45+5} {90}\\
& amp; =\ гідророзрив {50} {90}\\
&=\ розрив {50\ колір {лазурський} {\ div 10}} {90\ колір {\ div 10}}\\
&=\ frac {5} {9}
\ end {align*}\\\]

Відповідь

\(\frac{5}{9}\)

Приклад\(\PageIndex{16}\)

Спробуйте це! Додати:\(\frac{2}{30} + \frac{5}{21}\)

Відео Рішення:

(натисніть, щоб подивитися відео)

Приклад\(\PageIndex{17}\)

Спростити:\(2 \frac{1}{3} + \frac{3}{5} - \frac{1}{2}\)

Рішення

Почніть\(2 \frac{1}{3}\) з перетворення в неправильний дріб.

Відповідь:

\(2 \frac{13}{30}\)

Взагалі, краще працювати з неправильними фракціями. Однак, коли початкова задача включає мішані числа, якщо це доречно, представити свої відповіді у вигляді мішаних чисел. Крім того, мішані числа часто віддають перевагу при роботі з числами на числовому рядку і з реальними додатками.

Приклад\(\PageIndex{18}\)

Спробуйте це! Відніміть:\(\frac{5}{7} - 2 \frac{1}{7}\)

Відео Рішення:

(натисніть, щоб подивитися відео)

Приклад\(\PageIndex{19}\)

Скільки\(\frac{1}{2}\) дюймових книг у м'якій обкладинці можна скласти, щоб поміститися на полиці, яка висотою\(1 \frac{1}{2}\) футів?

Рішення

Для початку визначте висоту полиці в дюймах. Для цього використовуйте той факт, що в\(1\) футі є\(12\) дюйми і помножте наступним чином:

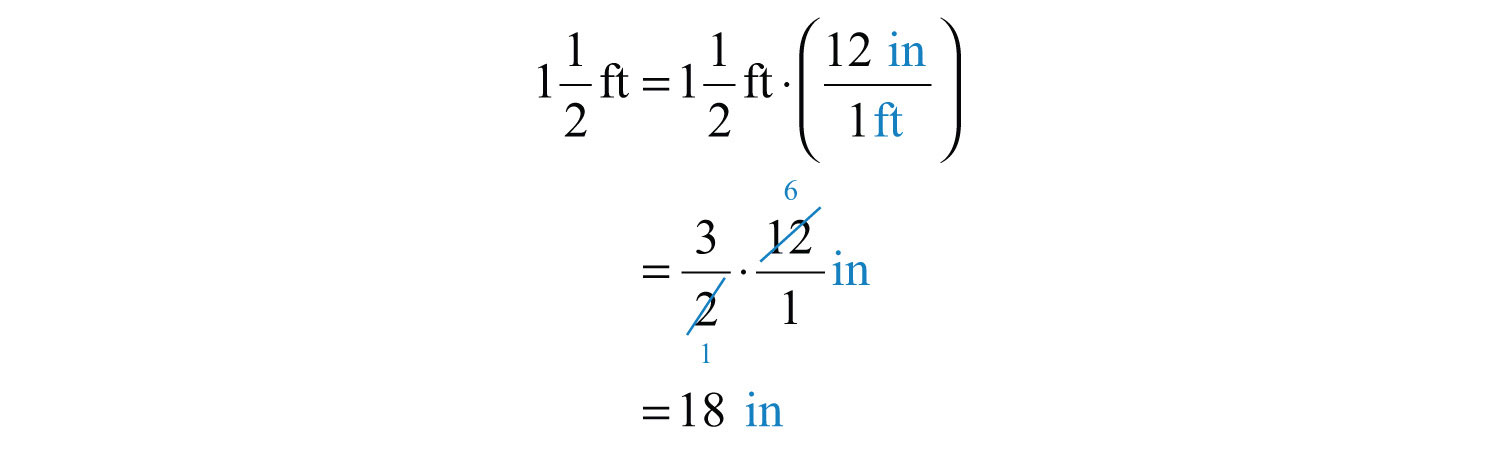
Далі визначте, скільки зошитів поміститься, розділивши висоту полиці на товщину кожної книги.

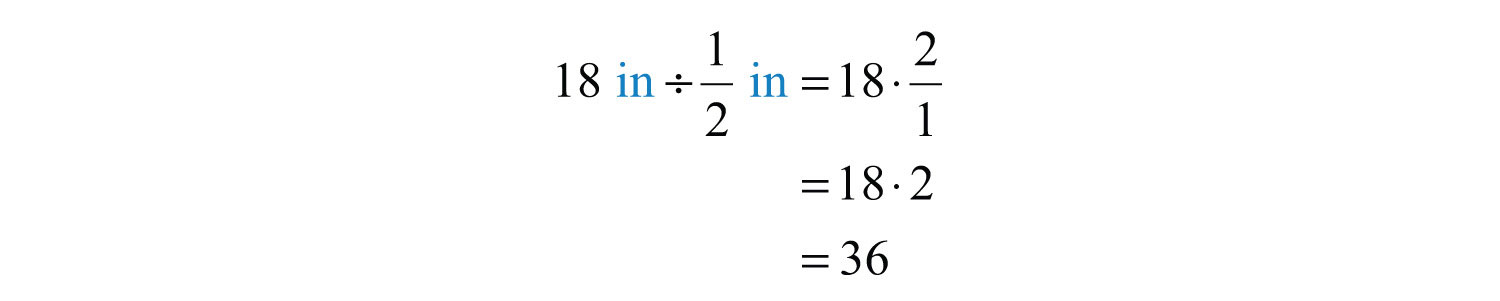
Відповідь

\(36\)книги можна укладати на полицю.

Ключові винос:

• Дроби не є унікальними; існує багато способів вираження одного і того ж співвідношення. Знайти еквівалентні дроби шляхом множення або ділення чисельника і знаменника на однакове дійсне число.
• Еквівалентні дроби в найнижчих вираженнях зазвичай є кращими. Це гарна практика, щоб завжди зменшити.
• В алгебрі зазвичай кращими є неправильні дроби. Однак у реальних додатках часто віддають перевагу еквівалентам змішаних чисел. Ми можемо представити відповіді як неправильні дроби, якщо оригінальне запитання не містить мішаних чисел, або це відповідь на реальну чи геометричну програму.
• Множення дробів не вимагає спільного знаменника; множте чисельники і множте знаменники для отримання добутку. Найкраще скасувати будь-які загальні множники в чисельнику та знаменнику перед множенням.
• Взаємні - це раціональні числа, добуток яких дорівнює\(1\). З огляду на дріб\(\frac{a}{b}\), його зворотний є\(\frac{b}{a}\).
• Ділимо дроби, множивши дивіденд на зворотний дільника. Іншими словами, помножте чисельник на зворотний знаменника.
• Перепишіть будь-яку проблему поділу як продукт перед скасуванням.
• Додавання або віднімання дробів вимагає спільного знаменника. Коли знаменники будь-якої кількості дробів збігаються, просто додайте або відніміть чисельники і запишіть результат над загальним знаменником.
• Перед додаванням або відніманням дробів переконайтеся, що знаменники однакові, знаходячи еквівалентні дроби із загальним знаменником. Помножте чисельник і знаменник кожного дробу на відповідне значення, щоб знайти еквівалентні дроби.
• Як правило, перед початком процесу додавання, віднімання, множення або ділення найкраще перетворити всі мішані числа в неправильні дроби.

Вправа\(\PageIndex{1}\)

Зменшіть кожну дробу до найнижчих показників.

1. \(\frac{5}{30}\)

2. \(\frac{6}{24}\)

3. \(\frac{30}{70}\)

4. \(\frac{18}{27}\)

5. \(\frac{44}{84}\)

6. \(\frac{54}{90}\)

7. \(\frac{135}{30}\)

8. \(\frac{105}{300}\)

9. \(\frac{18}{6}\)

10. \(\frac{256}{16}\)

11. \(\frac{126}{45}\)

12. \(\frac{52}{234}\)

13. \(\frac{54}{162}\)

14. \(\frac{2000}{3000}\)

15. \(\frac{270}{360}\)

Відповідь

1:\(1/6\)

3:\(3/7\)

5:\(11/21\)

7:\(9/2\)

9:\(3\)

11:\(14/5\)

13:\(1/3\)

15:\(3/4\)

Вправа\(\PageIndex{2}\)

Перепишіть як неправильний дріб.

1. \(4\frac{3}{4}\)
2. \(2\frac{1}{2}\)
3. \(5\frac{7}{15}\)
4. \(1\frac{1}{2}\)
5. \(3\frac{5}{8}\)
6. \(1\frac{3}{4}\)
7. \(−2\frac{1}{2}\)
8. \(−1\frac{3}{4}\)

Відповідь

1:\(5/2\)

3:\(3/2\)

5:\(7/4\)

7:\(−7/4\)

Вправа\(\PageIndex{3}\)

Перепишіть як мішане число.

1. \(\frac{15}{2}\)
2. \(\frac{9}{2}\)
3. \(\frac{40}{13}\)
4. \(\frac{103}{25}\)
5. \(\frac{73}{10}\)
6. \(\frac{−52}{7}\)
7. \(\frac{−59}{6}\)

Відповідь

2:\(4\frac{1}{2}\)

4:\(4\frac{3}{25}\)

6:\(−7\frac{3}{7}\)

Вправа\(\PageIndex{4}\)

Помножити і зменшити до найнижчих показників.

1. \(\frac{2}{3}⋅\frac{5}{7}\)
2. \(\frac{1}{5}⋅\frac{4}{8}\)
3. \(\frac{1}{2}⋅\frac{1}{3}\)
4. \(\frac{3}{4}⋅\frac{20}{9}\)
5. \(\frac{5}{7}⋅\frac{49}{10}\)
6. \(\frac{2}{3}⋅\frac{9}{12}\)
7. \(\frac{6}{14}⋅\frac{21}{12}\)
8. \(\frac{44}{15}⋅\frac{15}{11}\)
9. \(3 \frac{3}{4} \cdot 2 \frac{1}{3}\)
10. \(2\frac{7}{10}⋅5\frac{5}{6}\)
11. \(\frac{3}{11}(−\frac{5}{2})\)
12. \(-\frac{4}{5}(\frac{9}{5})\)
13. \((−\frac{9}{5} (−\frac{3}{10}) \)
14. \(\frac{6}{7}(−\frac{14}{3})\)
15. \((−\frac{9}{12})(−\frac{4}{8})\)
16. \(−\frac{3}{8}(−\frac{4}{15})\)
17. \(\frac{1}{7}⋅\frac{1}{2}⋅\frac{1}{3}\)
18. \(\frac{3}{5}⋅\frac{15}{21}⋅\frac{7}{27}\)
19. \(\frac{2}{5}⋅3\frac{1}{8}⋅\frac{4}{5}\)
20. \(2\frac{4}{9}⋅\frac{2}{5}⋅2\frac{5}{11}\)

Відповідь

1:\(10/21\)

3:\(1/6\)

5:\(7/2\)

7:\(3/4\)

9:\(834\)

11:\(−15/22\)

13:\(27/50\)

15:\(3/8\)

17:\(1/42\)

19:\(1\)

Вправа\(\PageIndex{5}\)

Визначте зворотні наступних чисел.

1. \(\frac{1}{2}\)
2. \(\frac{8}{5}\)
3. \(−\frac{2}{3}\)
4. \(−\frac{4}{3}\)
5. \(10\)
6. \(−4\)
7. \(2\frac{1}{3}\)
8. \(1\frac{5}{8}\)

Відповідь

1:\(2\)

3:\(−3/2\)

5:\(1/10\)

7:\(3/7\)

9:\(3/4\)

Вправа\(\PageIndex{6}\)

Розділити і звести до найнижчих термінів.

1. \(\frac{1}{2} \div \frac{2}{3}\)
2. \(\frac{5}{9} \div \frac{1}{3}\)
3. \(\frac{5}{8} \div (−\frac{4}{5})\)
4. \((−\frac{2}{5})÷\frac{15}{3}\)
5. \(\dfrac{−\frac{6}{7}}{−\frac{6}{7}}\)
6. \(\dfrac{−\frac{1}{2}}{\frac{1}{4}}\)
7. \(\dfrac{−\frac{10}{3}}{−\frac{5}{20}}\)
8. \(\dfrac{\frac{2}{3}}{\frac{9}{2}}\)
9. \(\dfrac{\frac{30}{50}}{\frac{5}{3}}\)
10. \(\dfrac{\frac{1}{2}}{2}\)
11. \(\dfrac{5}{\frac{2}{5}}\)
12. \(\dfrac{−6}{\frac{5}{4}}\)
13. \(2 \frac{1}{2} \div \frac{5}{3}\)
14. \(4 \frac{2}{3} \div 3 \frac{1}{2}\)
15. \(5 \div 2\frac{3}{5}\)
16. \(4\frac{3}{5} \div 23\)

Відповідь

1:\(3/4\)

3:\(−25/32\)

5:\(1\)

7:\(40/3\)

9:\(9/25\)

11:\(25/2\)

13:\(1 \frac{1}{2}\)

15:\(1 \frac{12}{13}\)

Вправа\(\PageIndex{7}\)

Додайте або відніміть і зменшуйте до найнижчих термінів.

1. \(\frac{17}{20}-\frac{5}{20}\)
2. \(\frac{4}{9}-\frac{13}{9}\)
3. \(\frac{3}{5}+\frac{1}{5}\)
4. \(\frac{11}{15}+\frac{9}{15}\)
5. \(\frac{5}{7}-2\frac{1}{7}\)
7. \(\frac{1}{2}+\frac{1}{3}\)
8. \(\frac{1}{5}-\frac{1}{4}\)
9. \(\frac{3}{4}-\frac{5}{2}\)
10. \(\frac{3}{8}+\frac{7}{16}\)
11. \(\frac{7}{15}-\frac{3}{10}\)
12. \(\frac{3}{10}+\frac{2}{14}\)
13. \(\frac{2}{30}+\frac{5}{21}\)
14. \(\frac{3}{18}-\frac{1}{24}\)
15. \(5 \frac{1}{2}+2\frac{1}{3}\)
16. \(1 \frac{3}{4}+2 \frac{1}{10}\)
17. \(\frac{1}{2}+\frac{1}{3}+\frac{1}{6}\)
18. \(\frac{2}{3}+\frac{3}{5}-\frac{2}{9}\)
19. \(\frac{7}{3}-\frac{3}{2}+\frac{2}{15}\)
20. \(\frac{9}{4}-\frac{3}{2}+\frac{3}{8}\)
22. \(\frac{2}{3}-4\frac{1}{2}+3\frac{1}{6}\)
23. \(1-\frac{6}{16}+\frac{3}{18}\)
24. \(3-\frac{1}{21}-\frac{1}{15}\)

Відповідь

1:\(3/5\)

3:\(4/5\)

5:\(−1 \frac{3}{7}\)

7:\(5/6\)

9:\(−7/4\)

11:\(1/6\)

13:\(32/105\)

15:\(7 \frac{5}{6}\)

17:\(1\)

19:\(29/30\)

21:\(2 \frac{2}{3}\)

23:\(19/24\)

Вправа\(\PageIndex{8}\)

Виконайте операції. Зменшіть відповіді до найнижчих термінів.

1. \(\frac{3}{14} \cdot \frac{7}{3} \div \frac{1}{8}\)
2. \(\frac{1}{2} \cdot (-\frac{4}{5}) \div \frac{14}{15}\)
3. \(\frac{1}{2} \div \frac{3}{4} \cdot \frac{1}{5}\)
4. \(-\frac{5}{9} \div \frac{5}{3} \cdot \frac{5}{2}\)
7. \(\frac{4}{5} \div 4 \cdot \frac{1}{2}\)
8. \(\frac{5}{3} \div 15 \cdot \frac{2}{3}\)
9. Що являє собою продукт\(\frac{3}{16}\) і\(\frac{4}{9}\)?
10. Що являє собою продукт\(−\frac{24}{5}\) і\(\frac{25}{8}\)?
11. Що таке частка\(\frac{5}{9}\) і\(\frac{25}{3}\)?
12. Що таке частка\(−\frac{16}{5}\) і\(32\)?
13. Відняти\(\frac{1}{6}\) від суми\(\frac{9}{2}\) і\(\frac{2}{3}\).
14. Відняти\(\frac{1}{4}\) від суми\(\frac{3}{4}\) і\(\frac{6}{5}\).
15. Яка загальна ширина, коли\(3\) дошки, кожна шириною в\(2 \frac{5}{8}\) дюйми, склеюються між собою?
16. Опади в дюймах для конкретних 3-денних вихідних були опубліковані як\(\frac{3}{10}\) дюйми в п'ятницю,\(1\frac{1}{2}\) дюйми в суботу та\(\frac{3}{4}\) дюйми в неділю. Розрахуйте загальну кількість опадів за цей період.
17. Дошку, яка довжиною\(5\frac{1}{4}\) ноги, повинна бути розрізана на\(7\) шматки однакової довжини. Яка довжина кожного шматка?
18. Скільки\(\frac{3}{4}\) дюймових ноутбуків товщиною можна скласти у коробку висотою\(2\) футів?
19. У класі математики одна чверть\(44\) учнів записалася на спеціальну суботню навчальну сесію. Скільки студентів записалося?
20. Визначити довжину огорожі потрібно, щоб підкласти прямокутну ручку з розмірами\(35\frac{1}{2}\) ноги по\(20\frac{2}{3}\) ногах.
21. Кожне коло навколо траси вимірює\(\frac{1}{4}\) милю. Скільки кіл потрібно для завершення пробігу\(2\frac{1}{2}\) милі?
22. Пенсіонер заробляв пенсію, яка складається з трьох чвертей його звичайної щомісячної зарплати. Якщо його регулярна місячна зарплата була\($5,200\), то якої щомісячної виплати пенсіонер може очікувати від пенсійного плану?

Відповідь

1:\(4\)

3:\(2/15\)

5:\(9/28\)

7:\(1/10\)

9:\(1/12\)

11:\(1/15\)

13:\(5\)

15:\(7 \frac{7}{8}\) дюйми

17:\(\frac{3}{4}\) фути

19:\(11\) студенти

21:\(10\) кола

Вправа\(\PageIndex{1}\)

Теми дискусійної дошки

1. Чи\(0\) є у відповідь? Поясніть.
2. Поясніть різницю між НКМ і ГКФ. Наведемо приклад.
3. Поясніть різницю між LCM і LCD.
4. Навіщо потрібно знаходити РК-дисплей, щоб скласти або відняти дроби?
5. Поясніть, як визначити, яка дріб більше,\(\frac{7}{16}\) або\(\frac{1}{2}\).