1.2: Додавання та віднімання цілих чисел
- Page ID
- 58092
Цілі навчання
- Додавання і віднімання цілих знаків.
- Перекладіть англійські речення, що включають додавання і віднімання, в математичні твердження.
- Обчисліть відстань між двома числами на числовому рядку.
Додавання і віднімання\((+, -)\)
Візуалізуйте додавання\(3 + 2\) на числовому рядку, перемістивши від нуля три одиниці вправо, а потім ще дві одиниці праворуч, як показано нижче:

На ілюстрації це видно\(3 + 2 = 5\). Аналогічно візуалізуйте додавання двох негативних чисел, спочатку\((−3) + (−2)\) перемістивши від початку три одиниці вліво, а потім перемістивши ще дві одиниці вліво.

У цьому прикладі показано на ілюстрації\((−3) + (−2) = −5\), що призводить до наступних двох властивостей дійсних чисел.
\[\begin{align*} & \color{Cerulean}{positive\ number\;} \color{Black}{+\;} \color{Cerulean}{positive\ number\;} \color{Black}{=\;} \color{Cerulean}{positive\ number} \\ & \color{Cerulean}{negative\ number\;} \color{Black}{+\;} \color{Cerulean}{negative\ number\;} \color{Black}{=\;} \color{Cerulean}{negative\ number} \end{align*}\]
Далі ми вивчимо додавання чисел з несхожими знаками. Щоб додати\(3 + (−7)\), спочатку перемістіть від початку три одиниці вправо, потім перемістіть сім одиниць ліворуч, як показано на малюнку:

У цьому випадку ми бачимо, що додавання від'ємного числа еквівалентно відніманню:
\(3+(-7)=3-7=-4\)
Спокусливо сказати, що позитивне число плюс негативне число є негативними, але це не завжди так:\(7+(−3)=7−3=4\). Результат додавання чисел з несхожими знаками може бути позитивним або негативним. Знак результату такий же, як і знак числа з найбільшою віддаленістю від початку. Наприклад, наступні результати залежать від знака числа,\(12\) оскільки воно знаходиться далі від нуля, ніж\(5\):
\[\begin{align*} &12+(-5)=7 \\ &-12+5=-7 \end{align*} \]
Приклад\(\PageIndex{1}\)
Спростити:\(14+(−25)\).
Рішення
\(−25\)Тут більша відстань від початку. Тому результат негативний.
\[\begin{align*} 14+(-25) &= 14-25 \\ &= -11 \end{align*}\]
Відповідь
\(-11\)
Властивості додавання
Задано будь-які дійсні числа \(a\)\(b\)\(c\), і, ми маємо такі властивості додавання:
- Властивість адитивної ідентичності:\[a+0=0+a=a\]
- Адитивна зворотна властивість:\[a+(−a)=(−a)+a=0\]
- Асоціативна властивість:\[(a+b)+c=a+(b+c)\]
- Комутативне майно:\[a+b=b+a\]
Нижче наведено кілька прикладів цих властивостей в дії.
Приклад\(\PageIndex{2}\)
Спростити:
а.\(5+0\)
б.\(10+(−10)\)
Рішення
а Додавання нуля до будь-якого дійсного числа призводить до того ж дійсного числа.
\[5+0=5 \nonumber\]
б Додавання протилежностей призводить до нуля.
Відповідь
а.\(5\); б.\(0\)
Приклад\(\PageIndex{3}\)
Спростити:
а.\((3+7)+4\)
б.\(3+(7+4)\)
Рішення
У дужках групуються операції, які слід виконати першими.
а.\[\begin{align*} (\color{Cerulean}{3+7} \color{Black}{)}+4 &= \color{Cerulean}{10}\ \color{Black}{+\ 4} \\ &= 14 \end{align*} \]
б.\[\begin{align*} 3+(\color{Cerulean}{7+4} \color{Black}{)} &= 3+ \color{Cerulean}{10} \\ &= 14 \end{align*} \]
Ці два приклади призводять до\(14\): зміна групування чисел не змінює результату.
\((\color{Cerulean}{3+7} \color{Black}{)} +4=3+(\color{Cerulean}{7+4} \color{Black}{)}=14\)
Відповідь
а.\(14\); б.\(14\)
На цьому етапі ми виділяємо той факт, що додавання є комутативним: порядок, в якому ми додаємо, не має значення і дає той самий результат.
\[\begin{align*} 2+9 &= 9+2 \\ 11 &= 11 \end{align*} \]
З іншого боку, віднімання не є комутативним.
\[\begin{align*} 2-9 &\neq 9-2 \\ -7 &\neq 7 \end{align*} \]
Ми будемо використовувати ці властивості, поряд з подвійно-негативним властивістю для дійсних чисел, для виконання більш задіяних послідовних операцій. Щоб спростити речі, ми зробимо загальним правилом спочатку замінити всі послідовні операції або додаванням або відніманням, а потім виконувати кожну операцію по порядку зліва направо.
Приклад\(\PageIndex{4}\)
Спростити:\(4−(−10)+(−5)\).
Рішення
Замініть послідовні операції, а потім виконайте їх зліва направо.
\[\begin{align*} 4-(-10)+(-5) &= 4+10-5 && \color{Cerulean}{Replace\ -(-)\ with\ addition\ (+).} \\ & && \color{Cerulean}{Replace\ +(-)\ with\ addition\ (-).} \\ &= 14-5 \\ &=9 \end{align*} \]
Відповідь
\(9\)
Приклад\(\PageIndex{5}\)
Спростити:\(−3+(−8)−(−7)\).
Рішення
\[\begin{align*} -3+(-8)-(-7) &= -3-8+7 && \color{Cerulean}{Replace\ +(-)\ with\ (-).} \\ & && \color{Cerulean}{Replace\ -(-)\ with\ (+).} \\ &= -11+7 \\ &=-4 \end{align*} \]
Відповідь
\(-4\)
Приклад\(\PageIndex{6}\)
Спробуйте це!
Спростити:\(12−(−9)+(−6)\).
Рішення
(натисніть, щоб подивитися відео)
Часто ми знаходимо необхідність перекладу англійських речень, що передбачають додавання і віднімання до математичних тверджень. Нижче перераховані деякі ключові слова, які переводять на дану операцію.
| Ключові слова | Операція |
| Сума, збільшена на, більше, ніж, плюс, додана до, загальна | \(+\) |
| Різниця, зменшена на, віднімається від, менше, мінус | \(-\) |
Приклад\(\PageIndex{7}\)
У чому різниця\(7\) і\(−3\)?
Рішення
Ключове слово «різниця» має на увазі, що ми повинні відняти числа.
\[\begin{align*} 7-(-3) &= 7+3 \\ &=10 \end{align*} \]
Відповідь
Різниця\(7\) і\(−3\) є\(10\).
Приклад\(\PageIndex{8}\)
Яка сума перших п'яти натуральних чисел?
Рішення
Початкове ключове слово, на якому слід зосередитись, - це «сума»; це означає, що ми додамо п'ять чисел. Перші п'ять натуральних чисел є\(\{1, 2, 3, 4, 5\}\). Нагадаємо, що не\(0\) є ні позитивним, ні негативним.
\(1+2+3+4+5=15\)
Відповідь
Сума перших п'яти натуральних чисел дорівнює\(15\).
Приклад\(\PageIndex{9}\)
Що\(10\) віднімається з суми\(8\) і\(6\)?
Рішення
Ми знаємо, що віднімання не є комутаційним; тому ми повинні подбати про віднімання в правильному порядку. Спочатку додайте,\(8\)\(6\) а потім відніміть\(10\) наступним чином:
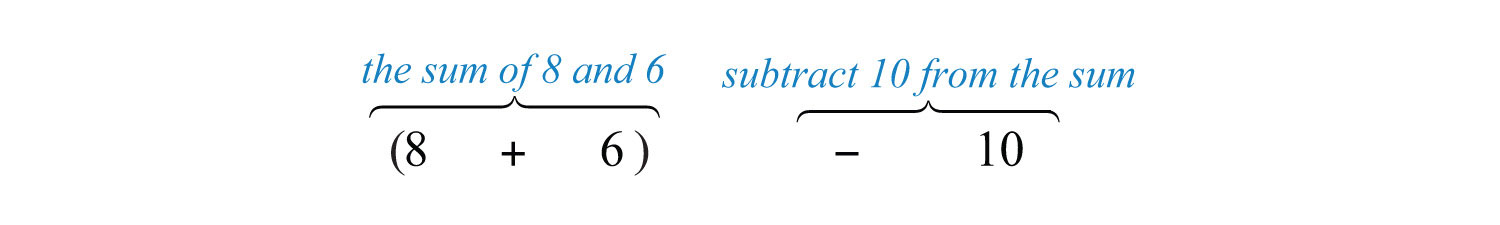
Важливо зауважити, що словосполучення «\(10\)віднімається з» не переводиться в математичне твердження в тому порядку, в якому воно з'являється. Іншими словами,\(10−(8+6)\) був би невірний переклад і призводить до неправильної відповіді. Після перекладу пропозиції виконайте операції.
\[\begin{align*} (8+6)-10 &= 14-10 \\ &= 4 \end{align*} \]
Відповідь
Десять віднімається від суми\(8\) і\(6\) є\(4\).
Відстань на числовому рядку
Одне застосування абсолютного значення полягає в тому, щоб знайти відстань між будь-якими двома точками на числовій лінії. Для дійсних чисел\(a\) і\(b\) формула відстані для числового рядка задається як,
\(d=|b-a|\)
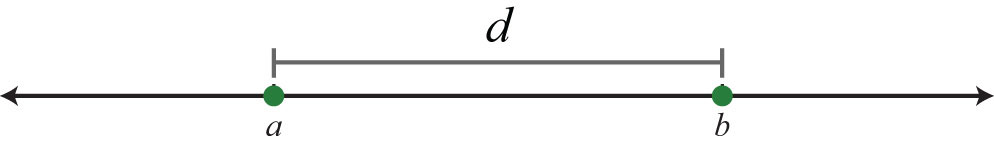
Приклад\(\PageIndex{10}\)
Визначте відстань між\(2\) і\(7\) на числовій лінії.
Рішення
На графіку ми бачимо, що відстань між двома заданими цілими числами є\(5\) одиницями.

За допомогою формули відстані отримуємо той же результат.
\[\begin{align*} d &= |7-2| \\ &=|5| \\ &=5 \end{align*} \]
Відповідь
\(5\)одиниць
Приклад\(\PageIndex{11}\)
Визначте відстань між\(−4\) і\(7\) на числовій лінії.
Рішення
Використовуйте формулу відстані для числового рядка\(d=|b−a|\), де\(a=−4\) і\(b=7\).
\[\begin{align*} d &= |7-(-4)| \\ &= |7+4| \\ &= |11| \\ &= 11 \end{align*} \]
Відповідь
\(11\)одиниць
Виходить, що неважливо, для яких балів використовуються\(a\) і\(b\); абсолютне значення завжди забезпечує позитивний результат.
| Використання\(a = −4\) і\(b = 7\) | Використання\(a = 7\) і\(b = −4\) |
| \(d=|7−(−4)|=|7+4|=|11|=11\) | \(d=|−4−7|=|−11|=11\) |
Вправа\(\PageIndex{1}\)
Визначте відстань між\(−12\) і\(−9\) на числовій лінії.
- Відповідь
-
3
Відео Рішення
(натисніть, щоб подивитися відео)
Ключові винос
- Позитивне число, додане до позитивного числа, є позитивним. Від'ємне число, додане до від'ємного числа, є від'ємним.
- Знак позитивного числа, доданого до від'ємного числа, такий же, як і знак числа з найбільшою відстанню від походження.
- Додавання є комутативним, а віднімання - ні.
- При спрощенні найкраще спочатку замінити послідовні операції, а потім працювати з операціями додавання та віднімання зліва направо.
- Відстань між будь-якими двома числами на числовому рядку є абсолютним значенням їх різниці. Іншими словами, задані будь-які дійсні числа a і b, використовуйте формулу\(d=|b−a|\) для обчислення відстані d між ними.
Вправа\(\PageIndex{2}\)
Додавання і віднімання.
- \(24+(−18)\)
- \(9+(−11)\)
- \(−31+5\)
- \(−12+15\)
- \(−30+(−8)\)
- \(−50+(−25)\)
- \(−7+(−7)\)
- \(−13−(−13)\)
- \(8−12+5\)
- \(−3−7+4\)
- \(−1−2−3−4\)
- \(6−(−5)+(−10)−14\)
- \(−5+(−3)−(−7)\)
- \(2−7+(−9)\)
- \(−30+20−8−(−18)\)
- \(10−(−12)+(−8)−20\)
- \(5−(−2)+(−6)\)
- \(−3+(−17)−(−13)\)
- \(−10+(−12)−(−20)\)
- \(−13+(−5)−(−25)\)
- \(20−(−4)−(−5)\)
- \(17+(−12)−(−2)\)
- Відповідь
-
1:6
3: −26
5: −38
7: −14
9:1
11: −10
13: −1
15:0
17:1
19: −2
21:29
Вправа\(\PageIndex{3}\)
Переведіть кожне речення в математичне твердження, а потім спростіть.
- Знайти суму\(3\)\(7\), і\(−8\).
- Знайти суму\(−12\)\(−5\), і\(7\).
- Визначте суму перших десяти натуральних чисел.
- Визначте суму цілих чисел у множині\(\{−2, −1, 0, 1, 2\}\).
- Знайдіть різницю\(10\) і\(6\).
- Знайдіть різницю\(10\) і\(−6\).
- Знайдіть різницю\(−16\) і\(−5\).
- Знайдіть різницю\(−19\) і\(7\).
- Відняти\(12\) від\(10\).
- Відняти\(−10\) від\(−20\).
- Відняти\(5\) від\(−31\).
- Відняти\(−3\) від\(27\).
- На два менше\(8\).
- На п'ять менше\(−10\).
- Відняти\(8\) від суми\(4\) і\(7\).
- Відняти\(-5\) від суми\(10\) і\(−3\).
- Відняти\(2\) від різниці\(8\) і\(5\).
- Відняти\(6\) від різниці\(−1\) і\(7\).
- Менді внесла\($200\) депозит на свій розрахунковий рахунок у вівторок. Потім вона писала\(4\) чеки на\($50.00\)\($125.00\),,\($60.00\), і\($45.00\). Скільки більше, ніж її депозит вона витратила?
- Захисник тричі пробіг м'яч у футбольному матчі минулої неділі. Він набирав\(7\) ярдів на одному пробігу, але втратив\(3\)\(8\) ярди та ярди на двох інших. Яким був його загальний метраж для гри?
- Дохід для місцевого фотографа за місяць становить\($1,200\). Його витрати включають в себе оренду студії\($600\), реквізит вартість\($105\), матеріали збори\($135\), і візажист, який бере плату\($120\). Яка його сумарна прибуток за місяць?
- Літак, що летить на\(30,000\) ногах, втратив\(2,500\) ноги на висоті, а потім\(1,200\) піднялися ноги. Яка нова висота літака?
- Температура була о\(22°\)\(6:00\) вечора і\(26°\) знизилася до півночі. Яка була температура опівночі?
- У медсестри є\(30\) мілілітри сольового розчину, але потрібні\(75\) мілілітри розчину. Скільки ще їй потрібно?
- Ширина прямокутника на\(2\) дюйми менше його довжини. Якщо довжина вимірює\(16\) дюйми, визначте ширину.
- Підстава трикутника -\(3\) ноги коротше його висоти. Якщо висота вимірює\(5\) ноги, знайдіть довжину підстави.
- Відповідь
-
1:\(2\)
3:\(55\)
5:\(4\)
7:\(−11\)
9:\(−2\)
11:\(−36\)
13:\(6\)
15:\(3\)
17:\(1\)
19:\($80\)
21:\($240\)
23:\(−4°\)
25:\(14\) дюйми
Вправа\(\PageIndex{4}\)
Знайти відстань між заданими числами на числовому рядку.
- \(−3\)і\(12\)
- \(8\)і\(−13\)
- \(−25\)і\(−10\)
- \(−100\)і\(−130\)
- \(−7\)і\(−20\)
- \(0\)і\(−33\)
- \(-10\)і\(10\)
- \(−36\)і\(36\)
- Найхолодніша температура на землі,\(−129°\) F, була зафіксована в 1983 році на станції Восток, Антарктида. Найгарячіша температура на землі,\(136°\) F, була зафіксована в 1922 році в Аль-Азізії, Лівія. Обчисліть діапазон температур Землі.
- Добова висока температура була зафіксована як\(91°\) F, а низька була зафіксована як\(63°\) F. Який був температурний діапазон за день?
- Учень заробив\(67\) бали на своєму найнижчому тесті і\(87\) бали на своєму кращому. Обчисліть його діапазон тестових балів.
- У напружений день певний веб-сайт може мати\(12,500\) хіти. У повільний день у нього може бути стільки ж, скільки\(750\) хітів. Обчисліть діапазон кількості звернень.
- Відповідь
-
1:\(15\) одиниці
3:\(15\) одиниці
5:\(13\) одиниці
7:\(20\) одиниці
9:\(265°\) Ф
11:\(20\) бали
Вправа\(\PageIndex{5}\)
Теми дискусійної дошки
- Поділіться прикладом додавання підписаних чисел у реальній програмі.
- Продемонструйте асоціативну властивість складання з будь-якими трьома дійсними числами.
- Показати, що віднімання не є комутативним
