3.5: Матриці та гаусова елімінація

Цілі навчання

• Використовуйте зворотну заміну для вирішення лінійних систем у верхній трикутній формі.
• Перетворення лінійних систем в еквівалентні доповнені матриці.
• Використовуйте матриці та гаусову елімінацію для розв'язання лінійних систем.

Заміна спини

Нагадаємо, що лінійна система рівнянь складається з безлічі двох і більше лінійних рівнянь з однаковими змінними. Лінійна система, що складається з трьох рівнянь у стандартній формі, розташованої так, що$x$ змінна не з'являється ні в одному рівнянні після першого, а$y$ змінна не з'являється ні в одному рівнянні після того, як другий, як кажуть, знаходиться у верхній трикутній формі. ²². Наприклад,

Малюнок$\PageIndex{1}$

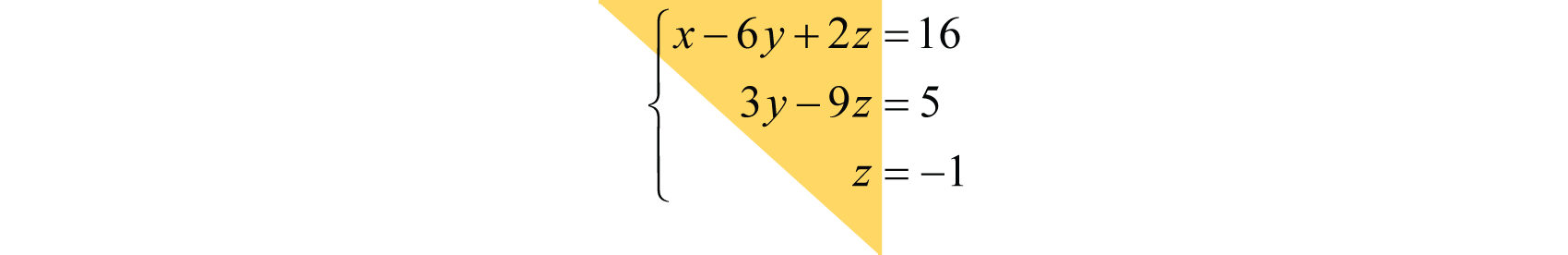
Зверніть увагу, що система утворює трикутник, де кожне наступне рівняння містить одну меншу змінну. Загалом,

$\color{Cerulean}{Linear\: Systems\: in\: Upper\: Triangular\: Form}$

$\left\{ \begin{array} { r l } { a _ { 1 } x + b _ { 1 } y = c _ { 1 } } \\ { b _ { 2 } y = c _ { 2 } }\end{array} \right. \quad\quad\left\{ \begin{array} { r l } { a _ { 1 } x + b _ { 1 } y + c_{1}z= d _ { 1 } } \\ { b _ { 2 } y + c_{2}z = d _ { 2 }\\ \\\quad\quad\:\:\: c_{3}z = d_{3} }\end{array} \right.$

Якщо лінійна система знаходиться в такому вигляді, ми можемо легко вирішити для однієї зі змінних, а потім назад замінити для вирішення інших змінних.

Приклад$\PageIndex{1}$:

Вирішити:$\left\{ \begin{aligned} 3 x - y & = 7 \\ 2 y & = - 2 \end{aligned} \right.$

Рішення

Нагадаємо, що розв'язки лінійних систем з двома змінними, якщо вони існують, є впорядкованими парами$(x, y)$. Ми можемо визначити$y$ -значення легко за допомогою другого рівняння.

$\begin{aligned} 2 y & = - 2 \\ y & = - 1 \end{aligned}$

Далі використовуємо перше рівняння$3x − y = 7$ і те, що$y = −1$ знайти$x$.

$\begin{aligned} 3 x - y & = 7 \\ 3 x - ( \color{Cerulean}{- 1}\color{black}{ )} & = 7 \\ 3 x + 1 & = 7 \\ 3 x & = 6 \\ x & = 2 \end{aligned}$

Відповідь:

$(2, -1)$

Приклад$\PageIndex{2}$:

Вирішити:$\left\{ \begin{aligned} x - 6 y + 2 z & = 16 \\ 3 y - 9 z & = 5 \\ z & = - 1 \end{aligned} \right.$.

Рішення

Нагадаємо, що розв'язки лінійних систем з трьома змінними, якщо вони існують, є впорядкованими трійками$(x, y, z)$. Використовуйте друге рівняння$3y − 9z = 5$ і те, що$z = −1$ знайти$y$.

$\begin{aligned} 3 y - 9 z & = 5 \\ 3 y - 9 (\color{Cerulean}{ - 1}\color{black}{ )} & = 5 \\ 3 y + 9 & = 5 \\ 3 y & = - 4 \\ y & = - \frac { 4 } { 3 } \end{aligned}$

Далі$z$ підставляємо$y$ і в перше рівняння.

$\begin{aligned} x - 6 y + 2 z & = 16 \\ x - 6 \left( \color{Cerulean}{- \frac { 4 } { 3} } \right) + 2 ( \color{Cerulean}{- 1}\color{black}{ )} & = 16 \\ x + 8 - 2 & = 16 \\ x + 6 & = 16 \\ x & = 10 \end{aligned}$

Відповідь:

$(10, -\frac{4}{3}, -1)$

Вправа$\PageIndex{1}$

Вирішити:$\left\{ \begin{aligned} 4 x - y + 3 z & = 1 \\ 2 y - 9 z & = - 2 \\ 3 z & = 2 \end{aligned} \right.$

Відповідь

$\left( \frac { 1 } { 4 } , 2 , \frac { 2 } { 3 } \right)$

www.youtube.com/В/RBUXJSQ-БВУ

Матриці та гаусова елімінація

У цьому розділі метою є розробка методики, яка впорядковує процес розв'язання лінійних систем. Почнемо з визначення матриці ²³, яка представляє собою прямокутний масив чисел, що складається з рядків і стовпців. З огляду на лінійну систему в стандартному вигляді, ми створюємо матрицю коефіцієнтів ²⁴, записуючи коефіцієнти, як вони виглядають збудованими без змінних або операцій наступним чином.

$\quad\quad\quad\quad\quad\color{Cerulean}{Linear\:System} \quad\quad\quad\quad\quad\color{Cerulean}{Coefficient\:Matrix} \\\left\{ \begin{array} { l } { a _ { 1 } x + b _ { 1 } y + c _ { 1 } z = d _ { 1 } } \\ { a _ { 2 } x + b _ { 2 } y + c _ { 2 } z = d _ { 2 } } \\ { a _ { 3 } x + b _ { 3 } y + c _ { 3 } z = d _ { 3 } } \end{array} \right. \quad \quad\Rightarrow\quad \quad \left[ \begin{array} { l } { a _ { 1 } b _ { 1 } c _ { 1 } } \\ { a _ { 2 } b _ { 2 } c _ { 2 } } \\ { a _ { 3 } b _ { 3 } c _ { 3 } } \end{array} \right]$

Рядки представляють коефіцієнти в рівняннях, а стовпці - коефіцієнти кожної змінної. Крім того, якщо ми включимо стовпець, який представляє константи, ми отримаємо те, що називається розширеною матрицею ²⁵. Для лінійної системи з двома змінними

$\quad\quad\quad\quad\color{Cerulean}{Linear\:System}\quad\color{Cerulean}\quad\quad{Augmented\:Matrix} \\\left\{ \begin{array} { l l } { a _ { 1 } x + b _ { 1 } y = c _ { 1 } } \\ { a _ { 2 } x + b _ { 2 } y = c _ { 2 } } \end{array} \right.\quad\quad \Leftrightarrow \quad\quad \left[ \begin{array} { l } { a _ { 1 } b _ { 1 } \left| c _ { 1 } \right. } \\ { a _ { 2 } b _ { 2 } \left| c _ { 2 } \right. } \end{array} \right]$

І для лінійної системи з трьома змінними у нас є

$\quad\quad\quad\quad\color{Cerulean}{Linear\:System}\quad\color{Cerulean}\quad\quad{Augmented\:Matrix} \\\left\{ \begin{array} { l } { a _ { 1 } x + b _ { 1 } y + c _ { 1 } z = d _ { 1 } } \\ { a _ { 2 } x + b _ { 2 } y + c _ { 2 } z = d _ { 2 } } \\ { a _ { 3 } x + b _ { 3 } y + c _ { 3 } z = d _ { 3 } } \end{array} \right.\quad\quad \Leftrightarrow \quad\left[ \begin{array} { l } { a _ { 1 } b _ { 1 } c _ { 1 } \left| d _ { 1 } \right. } \\ { a _ { 2 } b _ { 2 } c _ { 2 } \left| d _ { 2 } \right. } \\ { a _ { 3 } b _ { 3 } c _ { 3 } \left| d _ { 3 } \right. } \end{array} \right]$

Примітка

Пропунктирна вертикальна лінія забезпечує візуальний поділ між матрицею коефіцієнтів і стовпцем констант. В інших ресурсах алгебри, з якими ви можете зіткнутися, це іноді опускається.

Приклад$\PageIndex{3}$:

Побудувати доповнену матрицю, яка відповідає:$\left\{ \begin{array} { l } { 9 x - 6 y = 0 } \\ { - x + 2 y = 1 } \end{array} \right.$.

Рішення

Ця система складається з двох лінійних рівнянь у стандартній формі; отже, коефіцієнти в матриці виглядають так само, як і в системі.

$\left\{ \begin{array} { l } { 9 x - 6 y = 0 } \\ { - x + 2 y = 1 } \end{array} \right. \Leftrightarrow \left[ \begin{array} { c c | c } { 9 } & { - 6}&{0 } \\ { - 1 } &{ 2} &{ 1} \end{array} \right]$

Приклад$\PageIndex{4}$:

Побудувати доповнену матрицю, яка відповідає:$\left\{ \begin{aligned} x + 2 y - 4 z & = 5 \\ 2 x + y - 6 z & = 8 \\ 4 x - y - 12 z & = 13 \end{aligned} \right.$

Рішення

Оскільки рівняння наведені в стандартному вигляді, коефіцієнти з'являються в матриці так само, як і в системі.

$\left\{ \begin{array} { c c } { x + 2 y - 4 z = 5 } \\ { 2 x + y - 6 z = 8 } \\ { 4 x - y - 12 z = 13 } \end{array} \right. \Leftrightarrow \left[ \begin{array} { c c c | c } { 1 } & { 2 } & { - 4 } & { 5 } \\ { 2 } & { 1 } & { - 6 } & { 8 } \\ { 4 } & { - 1 } & { - 12 } & { 13 } \end{array} \right]$

Матриця має верхню трикутну форму, якщо всі елементи нижче початкового ненульового елемента в кожному наступному рядку дорівнюють нулю. Наприклад,

Малюнок$\PageIndex{2}$

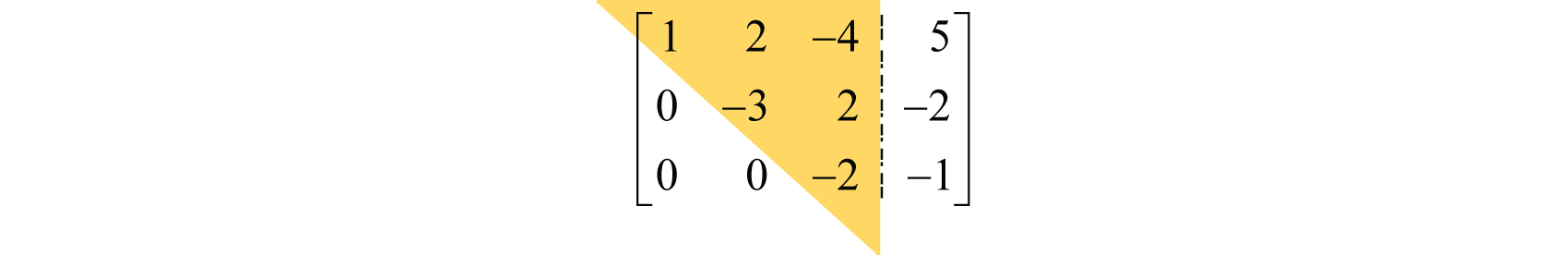
Зверніть увагу, що елементи нижче основної діагоналі дорівнюють нулю, а наведені вище коефіцієнти утворюють трикутну форму. Загалом,

$\color{Cerulean}{Upper\:Triangular\:Form}\\\left[ \begin{array} { c c } { a _ { 1 }} & { b _ { 1 } } \\ { 0} &{ b _ { 2 } } \end{array} \right] \quad \left[ \begin{array} { c c c } { a _ { 1 }} &{ b _ { 1 }} & { c _ { 1 } } \\ { 0} &{ b _ { 2 }}&{ c _ { 2 } } \\ { 0 } & { 0} &{ c _ { 3 } } \end{array} \right]$

Це важливо, оскільки в цьому розділі ми окреслимо процес, за допомогою якого можуть бути зроблені певні операції для створення еквівалентної лінійної системи у верхній трикутній формі, щоб її можна було вирішити за допомогою зворотної заміни. Огляд процесу викладено нижче:

Малюнок$\PageIndex{3}$

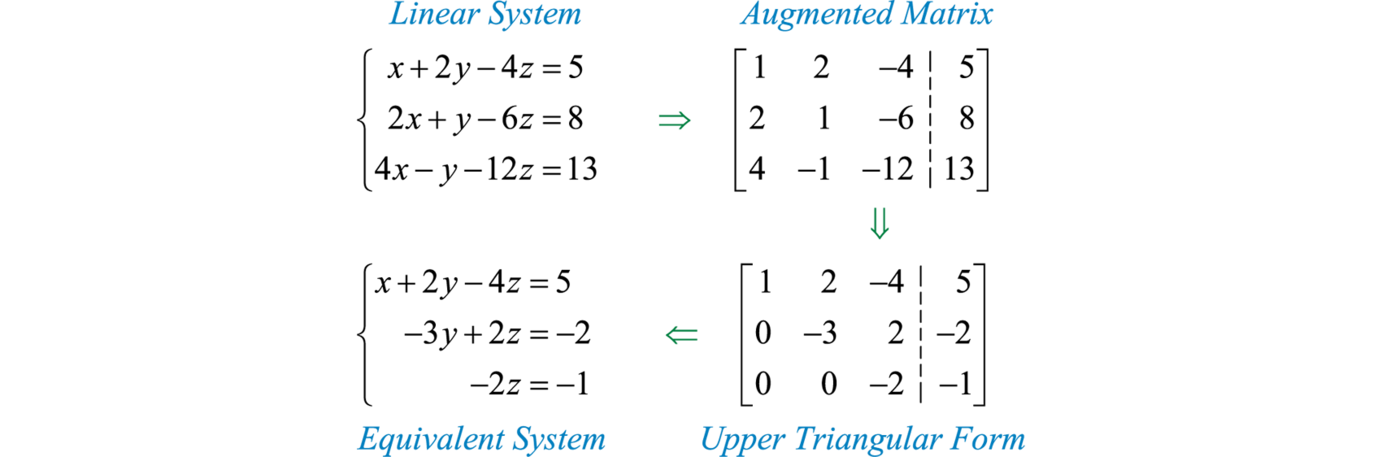
Після того, як система знаходиться у верхній трикутній формі, ми можемо використовувати зворотну заміну, щоб легко її вирішити. Важливо відзначити, що представлені тут доповнені матриці представляють лінійні системи рівнянь в стандартному вигляді.

Наступні елементарні операції рядків ²⁶ призводять до розширеної матриці, що представляють еквівалентні лінійні системи:

1. Будь-які два ряди можуть бути змінені місцями.
2. Кожен елемент в рядку можна помножити на ненульову константу.
3. Будь-який рядок може бути замінений сумою цього рядка і кратною іншому рядку.

Примітка

Ці операції узгоджуються з властивостями, використовуваними в методі усунення.

Для ефективного розв'язання системи лінійних рівнянь спочатку будують доповнену матрицю. Потім застосуйте відповідні елементарні операції рядка для отримання розширеної матриці у верхній трикутній формі. У такому вигляді еквівалентна лінійна система може бути легко вирішена за допомогою зворотної заміни. Цей процес називається гауссівською ліквідацією ²⁷, названий на честь Карла Фрідріха Гаусса (1777—1855).

Ілюстрація$\PageIndex{4}$: Карл Фрідріх Гаусс

Етапи розв'язання лінійного рівняння з двома змінними за допомогою гаусової елімінації наведені в наступному прикладі.

Приклад$\PageIndex{5}$:

Вирішити за допомогою матриць і гаусової елімінації:$\left\{ \begin{array} { l } { 9 x - 6 y = 0 } \\ { - x + 2 y = 1 } \end{array} \right.$.

Рішення

Переконайтеся, що рівняння в системі знаходяться в стандартній формі перед початком цього процесу.

Крок 1: Побудуйте відповідну розширену матрицю.

$\left\{ \begin{array} { l } { 9 x - 6 y = 0 } \\ { - x + 2 y = 1 } \end{array} \right. \Leftrightarrow \left[ \begin{array} { c c | c} { 9} &{ - 6} & {0 } \\ { - 1} &{2}&{1 } \end{array} \right]$

Крок 2: Застосуйте операції елементарного ряду, щоб отримати верхню трикутну форму. В цьому випадку нам потрібно лише усунути перший елемент другого ряду,$−1$. Для цього другий ряд множимо на$9$ і додаємо його в перший ряд.

Малюнок$\PageIndex{5}$

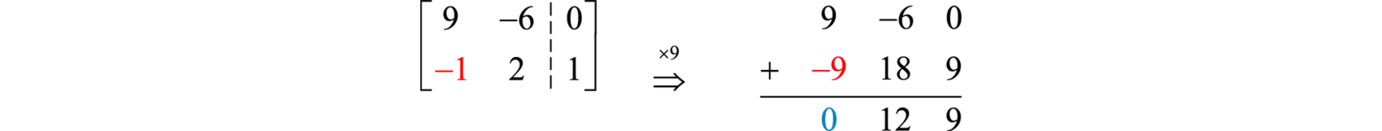
Тепер скористайтеся цим, щоб замінити другий ряд.

$\left[ \begin{array} { c c | c } { 9 } & { - 6}&{0 } \\ {\color{Cerulean}{ 0} } & { \color{black}{12} } & { 19 } \end{array} \right]$

Це призводить до збільшення матриці у верхній трикутній формі.

Крок 3: Перетворіть назад в лінійну систему та вирішуйте за допомогою зворотної заміни. У цьому прикладі ми маємо

$\left[ \begin{array} { c c |c} { 9} &{ - 6} &{0 } \\ { \color{Cerulean}{0} } & { \color{black}{12}} &{ 9 } \end{array} \right] \Rightarrow \left\{ \begin{array} { r } { 9 x - 6 y = 0 } \\ { 12 y = 9 } \end{array} \right.$

Розв'яжіть друге рівняння для$y$,

$\begin{array} { l } { 12 y = 9 } \\ { y = \frac { 9 } { 12 } } \\ { y = \frac { 3 } { 4 } } \end{array}$

Заставте це значення$y$ в перше рівняння, яке потрібно знайти$x$,

$\begin{aligned} 9 x - 6 y & = 0 \\ 9 x - 6 \left( \color{OliveGreen}{\frac { 3 } { 4 }} \right) & = 0 \\ 9 x - \frac { 9 } { 2 } & = 0 \\ 9 x & = \frac { 9 } { 2 } \\ x & = \frac { 1 } { 2 } \end{aligned}$

Відповідь:

$\left( \frac { 1 } { 2 } , \frac { 3 } { 4 } \right)$

Етапи використання гаусової елімінації для розв'язання лінійного рівняння з трьома змінними наведені в наступному прикладі.

Приклад$\PageIndex{6}$:

Вирішіть за допомогою матриць і гаусової елімінації:$\left\{ \begin{array} { c } { x + 2 y - 4 z = 5 } \\ { 2 x + y - 6 z = 8 } \\ { 4 x - y - 12 z = 13 } \end{array} \right.$

Рішення

Переконайтеся, що рівняння в системі знаходяться в стандартній формі перед початком цього процесу.

Крок 1: Побудуйте відповідну розширену матрицю.

$\left\{ \begin{array} { c c c } { x + 2 y - 4 z } & { = 5 } \\ { 2 x + y - 6 z } & { = 8 } \\ { 4 x - y - 12 z } & { = 13 } \end{array} \right.\quad \color{Cerulean}{\Rightarrow} \color{black}{\quad \left[ \begin{array} { c c c | c } { 1 } & { 2 } & { - 4 } & { 5 } \\ { 2 } & { 1 } & { - 6 } & { 8 } \\ { 4 } & { - 1 } & { - 12 } & { 13 } \end{array} \right]}$

Крок 2: Застосуйте операції елементарного ряду, щоб отримати верхню трикутну форму. Починаємо з усунення першого елемента другого ряду,$2$ в даному випадку. Для цього помножте перший ряд на,$−2$ а потім додайте його до другого ряду.

$\left[ \begin{array} { r r r | r } { 1 } & { 2 } & { - 4 } & { 5 } \\ { \color{red}{2} } & { 1 } & { - 6 } & { 8 } \\ { 4 } & { - 1 } & { - 12 } & { 13 } \end{array} \right] \stackrel{\stackrel {\times( - 2 )}{\Longrightarrow}}{}\begin{array} { c c c c }\:\;\:\:\:\: { - 2} &{ - 4} &\:\:{ 8} &{ - 10 } \\ + \:\:\:\:\:\:{ \color{red}{2}} & {\color{black}{1}} & {- 6} &{8 } \\ \hline \:\:\:\:\:\:\:\: {\color{Cerulean}{0}} &{ - 3} & {2} & { - 2 } \end{array}$

Використовуйте це для заміни другого ряду.

$\left[ \begin{array} { r r r | r } { 1 } & { 2 } & { - 4 } & { 5 } \\ { \color{Cerulean}{0} } & { \color{black}{- 3} } & { 2 } & { - 2 } \\ { 4 } & { - 1 } & { - 12 } & { 13 } \end{array} \right]$

Далі виключіть перший елемент третього ряду,$4$ в цьому випадку множивши перший ряд на$−4$ і додаючи його до третього ряду.

$\left[ \begin{array} { r r r | r } { 1 } & { 2 } & { - 4 } & { 5 } \\ { 0 } & { -3 } & { 2 } & { -2 } \\ { \color{red}{4} } & { \color{black}{- 1} } & { - 12 } & { 13 } \end{array} \right] \stackrel{\stackrel {\times( - 4 )}{\Longrightarrow}}{}\begin{array} { c c c c }\:\;\:\:\:\: { - 4} &{ - 8} &{ 16} &{ - 20 } \\ + \:\:\:\:\:\:{ \color{red}{4}} & {\color{black}{-1}} & {- 12} &{13 } \\ \hline \:\:\:\:\:\:\:\: {\color{Cerulean}{0}} &{ - 9} & {4} & { - 7 } \end{array}$

Використовуйте це для заміни третього ряду.

$\left[ \begin{array} { r r r | r } { 1 } & { 2 } & { - 4 } & { 5 } \\ {\color{Cerulean}{ 0} } & { \color{black}{- 3} } & { 2 } & { - 2 } \\ { \color{Cerulean}{0} } & { \color{black}{- 9} } & { 4 } & { - 7 } \end{array} \right]$

Це призводить до розширеної матриці, де елементи під першим елементом першого рядка дорівнюють нулю. Далі усуваємо другий елемент в третьому ряду, в даному випадку$−9$. Другий ряд множимо на$−3$ і додаємо до третього ряду.

Малюнок$\PageIndex{6}$

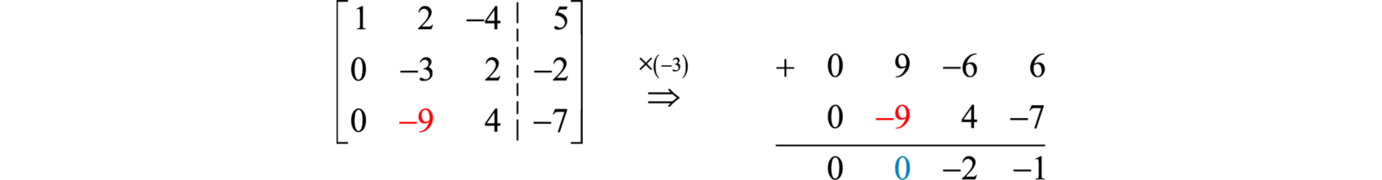
Використовуйте це, щоб замінити третій рядок, і ми бачимо, що ми отримали матрицю у верхній трикутній формі.

$\left[ \begin{array} { r r r | r } { 1 } & { 2 } & { - 4 } & { 5 } \\ { \color{Cerulean}{0} } & { \color{black}{- 3} } & { 2 } & { - 2 } \\ { \color{Cerulean}{0} } & { \color{Cerulean}{0} } & {\color{black}{ - 2} } & { - 1 } \end{array} \right]$

Крок 3: Перетворіть назад в лінійну систему та вирішуйте за допомогою зворотної заміни. У цьому прикладі ми маємо

$\left[ \begin{array} { c c c |c } { 1 } & { 2 } & { - 4 } & { 5 } \\ { 0 } & { - 3 } & { 2 } & { - 2 } \\ { 0 } & { 0 } & { - 2 } & { - 1 } \end{array} \right] \Rightarrow \left\{ \begin{array} { r } { x + 2 y - 4 z = 5 } \\ { - 3 y + 2 z = - 2 } \\ { - 2 z = - 1 } \end{array} \right.$

Відповідь:

Це залишається читачеві, щоб переконатися, що рішення є$(5, 1, \frac{1}{2})$.

Примітка

Як правило, робота, пов'язана із заміною рядка множенням і додаванням, виконується збоку за допомогою скретч-паперу.

Приклад$\PageIndex{7}$:

Вирішіть за допомогою матриць і гаусової елімінації:$\left\{ \begin{aligned} 2 x - 9 y + 3 z &= - 18 \\ x - 2 y - 3 z &= - 8 \\ - 4 x + 23 y + 12 z &= 47 \end{aligned} \right.$

Рішення

Починаємо з перетворення системи в доповнену матрицю коефіцієнтів.

$\left\{ \begin{aligned} 2 x - 9 y + 3 z &= - 18 \\ x - 2 y - 3 z& = - 8 \\ - 4 x + 23 y + 12 z &= 47 \end{aligned} \right. \color{OliveGreen}{\Rightarrow} \color{black}{\left[ \begin{array} { c c c | c } { 2 }&{- 9 } & { 3} &{ - 18 } \\ { 1} &{ - 2 } & { - 3 } & { - 8 } \\ { - 4 } & { 23 } & { 12 } & { 47 } \end{array} \right]}$

Елементарні операції рядків спрощуються, якщо провідним ненульовим елементом у рядку є$1$. З цієї причини починайте з перемикання ряду один і два.

Малюнок$\PageIndex{7}$

Замініть рядок два сумою$−2$ разів на рядок один і другий рядок.

Малюнок$\PageIndex{8}$

Замініть рядок три сумою$4$ разів на рядок перший і рядок три.

Малюнок$\PageIndex{9}$

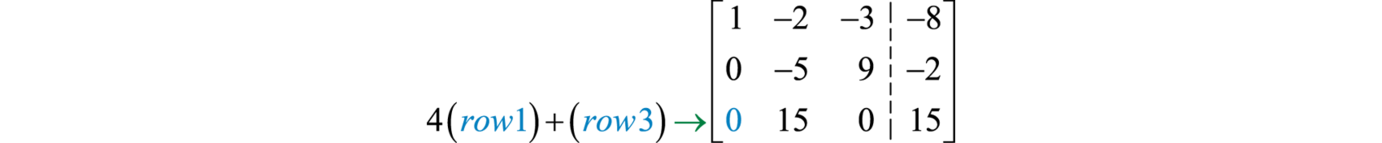
Далі ділимо ряд$3$ на$15$.

Малюнок$\PageIndex{10}$

Пересадочний ряд три з рядом два.

Малюнок$\PageIndex{11}$

Далі$3$ замініть рядок сумою$5$ разів рядка два та три рядки.

Малюнок$\PageIndex{12}$

Це призводить до матриці у верхній трикутній формі. Матриця знаходиться в рядковій формі ешелону ²⁸, якщо вона знаходиться у верхній трикутній формі, де провідний ненульовий елемент кожного рядка$1$. Ми можемо отримати цю форму, замінивши рядок три з результатами ділення його на$9$.

Малюнок$\PageIndex{13}$

Перетворити в систему лінійних рівнянь і вирішити шляхом зворотної підстановки.

$\left[ \begin{array} { c c c | c} { 1} &{ - 2} &{ - 3} &{ - 8 } \\ { 0 } & { 1 } & { 0 } & { 1 } \\ { 0 } & { 0 } & { 1 } & { \frac { 1 } { 3 } } \end{array} \right] \Rightarrow \left\{ \begin{aligned} x - 2 y - 3 z & = - 8 \\ y & = 1 \\ z & = \frac { 1 } { 3 } \end{aligned} \right.$

Ось$y = 1$ і$z = \frac{1}{3}$. Підставте в перше рівняння, яке потрібно знайти$x$.

$\begin{aligned} x - 2 y - 3 y & = - 8 \\ x - 2 ( \color{Cerulean}{1}\color{black}{ )} - 3 \left(\color{Cerulean}{ \frac { 1 } { 3} } \right) & = - 8 \\ x - 2 - 1 & = - 8 \\ x - 3 & = - 8 \\ x & = - 5 \end{aligned}$

Відповідь:

Тому рішення є$\left( - 5,1 , \frac { 1 } { 3 } \right)$.

Примітка

Багато сучасних калькуляторів і систем комп'ютерної алгебри можуть виконувати гаусову елімінацію. Для початку потрібно буде дізнатися, як ввести матрицю. Потім скористайтеся функціями калькулятора, щоб знайти форму ешелону рядків. Вам рекомендується провести деякі веб-дослідження на цю тему для вашої конкретної моделі калькулятора.

Вправа$\PageIndex{2}$

Вирішіть за допомогою гаусової елімінації:$\left\{ \begin{array} { c } { x - 3 y + 2 z = 16 } \\ { 4 x - 11 y - z = 69 } \\ { 2 x - 5 y - 4 z = 36 } \end{array} \right.$.

Відповідь

$( 6 , - 4 , - 1 )$

www.youtube.com/В/8 МаввигоЄДМ

Приклад$\PageIndex{8}$:

Вирішити за допомогою матриць і гаусової елімінації:$\left\{ \begin{array} { c } { x - 2 y + z = 4 } \\ { 2 x - 3 y + 4 z = 7 } \\ { 4 x - 7 y + 6 z = 15 } \end{array} \right.$.

Рішення

Починаємо з перетворення системи в доповнену матрицю коефіцієнтів.

$\left\{ \begin{array} { c c } { x - 2 y + z = 4 } \\ { 2 x - 3 y + 4 z = 7 } \\ { 4 x - 7 y + 6 z = 15 } \end{array} \right. \color{OliveGreen}{\Rightarrow} \color{black}{ \left[ \begin{array} { c c | c } { 1} &{ - 21} &{ 4 } \\ { 2} &{ - 34}&{ 7 } \\ { 4} &{ - 76}&{ 15 } \end{array} \right]}$

Замініть рядок два на$−2$ (рядок$1$) + (рядок$2$) і замініть рядок третій на$−4$ (рядок$1$) + (рядок$3$).

$\left[ \begin{array} { c c |c } { 1 } & { - 21 } & { 4 } \\ { 0 } & { 12 } & { - 1 } \\ { 0 } & { 12 } & { - 1 } \end{array} \right]$

Замініть рядок три на$−1$ (рядок$2$) + (рядок$3$).

$\left[ \begin{array} { c c | c} { 1 } & { - 21 } & { 4 } \\ { 0 } & { 12 } & { - 1 } \\ { 0 } & { 00 } & { 0 } \end{array} \right]$

Останній рядок вказує на те, що це залежна система, оскільки перетворення доповненої матриці назад до рівнянь, які ми маємо,

$\left\{ \begin{aligned} x - 2 y + z & = 4 \\ y + 2 z & = - 1 \\ 0 x + 0 y + 0 z & = 0 \end{aligned} \right.$

Зверніть увагу, що рядок нулів відповідає наступному ідентичності,

$\begin{array} { r } { 0 x + 0 y + 0 z = 0 } \\ { 0 = 0 } \end{array} \color{Cerulean}{✓}$

У цьому випадку ми можемо висловити нескінченно багато рішень з точки зору$z$. З другого ряду у нас виходить наступне:

$\begin{aligned} y + 2 z & = - 1 \\ y & = - 2 z - 1 \end{aligned}$

І з першого рівняння,

$\begin{aligned} x - 2 y + z & = 4 \\ x - 2 ( \color{Cerulean}{- 2 z - 1}\color{black}{ )} + z & = 4 \\ x + 5 z + 2 & = 4 \\ x & = - 5 z + 2 \end{aligned}$

Рішення набувають вигляду,$(x, y, z) = (−5z + 2, −2z − 1, z)$ де$z$ знаходиться будь-яке дійсне число.

Відповідь:

$( - 5 z + 2 , - 2 z - 1 , z )$

Залежні і непослідовні системи можуть бути ідентифіковані в доповненій матриці коефіцієнтів, коли коефіцієнти в одному рядку дорівнюють нулю.

Малюнок$\PageIndex{14}$

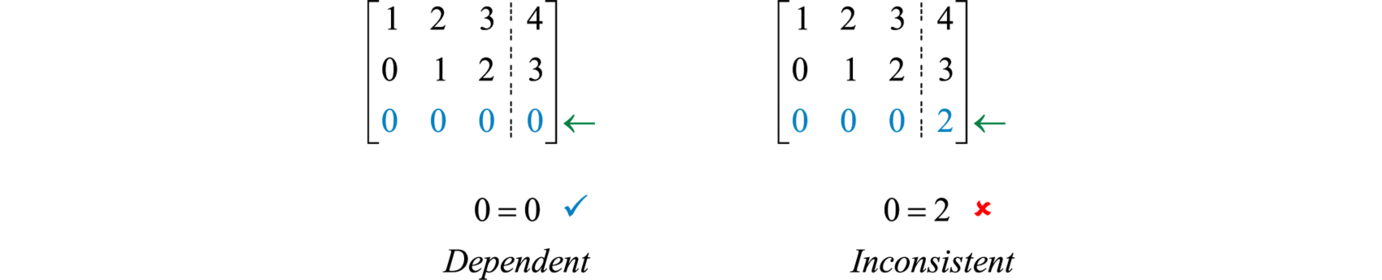
Якщо рядок нулів має відповідну константу нуля, то матриця являє собою залежну систему. Якщо константа ненульова, то матриця являє собою неузгоджену систему.

Вправа$\PageIndex{3}$

Вирішити за допомогою матриць і гаусової елімінації:$\left\{ \begin{aligned} 5 x - 2 y + z & = - 3 \\ 10 x - y + 3 z & = 0 \\ - 15 x + 9 y - 2 z & = 17 \end{aligned} \right.$.

Відповідь

$\varnothing$

www.youtube.com/В/38W0EB5E0py

Ключові виноси

• Лінійна система у верхній трикутній формі може бути легко вирішена за допомогою зворотного заміщення.
• Доповнена матриця коефіцієнтів і гаусова елімінація можуть бути використані для впорядкування процесу розв'язання лінійних систем.
• Для розв'язання системи з використанням матриць і гауссова елімінації спочатку використовують коефіцієнти для створення доповненої матриці. Застосовуйте елементарні операції рядка як засіб для отримання матриці у верхній трикутній формі. Перетворіть матрицю назад в еквівалентну лінійну систему і вирішіть її за допомогою зворотної заміни.

Вправа$\PageIndex{4}$

Вирішити за допомогою зворотної заміни.

1. $\left\{ \begin{aligned} 5 x - 3 y & = 2 \\ y & = - 1 \end{aligned} \right.$
2. $\left\{ \begin{array} { r } { 3 x + 2 y = 1 } \\ { y = 3 } \end{array} \right.$
3. $\left\{ \begin{aligned} x - 4 y & = 1 \\ 2 y & = - 3 \end{aligned} \right.$
4. $\left\{ \begin{aligned} x - 5 y & = 3 \\ 10 y & = - 6 \end{aligned} \right.$
5. $\left\{ \begin{aligned} 4 x - 3 y & = - 16 \\ 7 y & = 0 \end{aligned} \right.$
6. $\left\{ \begin{aligned} 3 x - 5 y & = - 10 \\ 4 y & = 8 \end{aligned} \right.$
7. $\left\{ \begin{aligned} 2 x + 3 y & = - 1 \\ 3 y & = 2 \end{aligned} \right.$
8. $\left\{ \begin{aligned} 6 x - y & = - 3 \\ 4 y & = 3 \end{aligned} \right.$
9. $\left\{ \begin{aligned} x - y & = 0 \\ 2 y & = 0 \end{aligned} \right.$
10. $\left\{ \begin{aligned} 2 x + y & = 2 \\ 3 y & = 0 \end{aligned} \right.$
11. $\left\{ \begin{aligned} x + 3 y - 4 z & = 1 \\ y - 3 z & = - 2 \\ z & = 3 \end{aligned} \right.$
12. $\left\{ \begin{aligned} x - 5 y + 4 z & = - 1 \\ y - 7 z & = 10 \\ z & = - 2 \end{aligned} \right.$
13. $\left\{ \begin{aligned} x - 6 y + 8 z & = 2 \\ 3 y - 4 z & = - 4 \\ 2 z & = - 1 \end{aligned} \right.$
14. $\left\{ \begin{aligned} 2 x - y + 3 z & = - 9 \\ 2 y + 6 z & = - 2 \\ 3 z & = 2 \end{aligned} \right.$
15. $\left\{ \begin{aligned} 10 x - 3 y + z & = 13 \\ 11 y - 3 z & = 9 \\ 2 z & = - 6 \end{aligned} \right.$
16. $\left\{ \begin{aligned} 3 x - 2 y + 5 z & = - 24 \\ 4 y + 5 z & = 3 \\ 4 z & = - 12 \end{aligned} \right.$
17. $\left\{ \begin{aligned} x - y + 2 z & = 1 \\ 2 y + z & = 1 \\ 3 z & = - 1 \end{aligned} \right.$
18. $\left\{ \begin{aligned} x + 2 y - z & = 2 \\ y - 3 z & = 1 \\ 6 z & = 1 \end{aligned} \right.$
19. $\left\{ \begin{aligned} x - 9 y + 5 z & = - 3 \\ 2 y & = 10 \\ 3 z & = 27 \end{aligned} \right.$
20. $\left\{ \begin{aligned} 4 x - z & = 3 \\ 3 y - 2 z & = - 1 \\ 2 z & = - 8 \end{aligned} \right.$

Відповідь

1. $\left( - \frac { 1 } { 5 } , - 1 \right)$

3. $\left( - 5 , - \frac { 3 } { 2 } \right)$

5. $(-4, 0)$

7. $\left( - \frac { 3 } { 2 } , \frac { 2 } { 3 } \right)$

9. $(0,0)$

11. $(-8, 7, 3)$

13. $\left( - 6 , - 2 , - \frac { 1 } { 2 } \right)$

15. $\left( \frac { 8 } { 5 } , 0 , - 3 \right)$

17. $\left( \frac { 7 } { 3 } , \frac { 2 } { 3 } , - \frac { 1 } { 3 } \right)$

19. $(-3, 5, 9)$

Вправа$\PageIndex{5}$

Побудувати відповідну доповнену матрицю (не вирішувати).

1. $\left\{ \begin{array} { c } { x + 2 y = 3 } \\ { 4 x + 5 y = 6 } \end{array} \right.$
2. $\left\{ \begin{array} { l } { 6 x + 5 y = 4 } \\ { 3 x + 2 y = 1 } \end{array} \right.$
3. $\left\{ \begin{array} { l } { x - 2 y = 1 } \\ { 2 x - y = 1 } \end{array} \right.$
4. $\left\{ \begin{array} { c } { x - y = 2 } \\ { - x + y = - 1 } \end{array} \right.$
5. $\left\{ \begin{aligned} - x + 8 y & = 3 \\ 2 y & = 2 \end{aligned} \right.$
6. $\left\{ \begin{array} { r } { 3 x - 2 y = 4 } \\ { - y = 5 } \end{array} \right.$
7. $\left\{ \begin{array} { l } { 3 x - 2 y + 7 z = 8 } \\ { 4 x - 5 y - 10 z = 6 } \\ { - x - 3 y + 2 z = - 1 } \end{array} \right.$
8. $\left\{ \begin{array} { c } { x - y - z = 0 } \\ { 2 x - y + 3 z = - 1 } \\ { - x + 4 y - 3 z = - 2 } \end{array} \right.$
9. $\left\{ \begin{aligned} x - 9 y + 5 z & = - 3 \\ 2 y & = 10 \\ 3 z & = 27 \end{aligned} \right.$
10. $\left\{ \begin{array} { c } { 4 x - z = 3 } \\ { 3 y - 2 z = - 1 } \\ { 2 z = - 8 } \end{array} \right.$
11. $\left\{ \begin{array} { c } { 8 x + 2 y = - 13 } \\ { - 2 y + z = 1 } \\ { 12 x - 5 z = - 18 } \end{array} \right.$
12. $\left\{ \begin{array} { l } { x - 3 z = 2 } \\ { y + 6 z = 4 } \\ { 2 x + 3 y = 12 } \end{array} \right.$

Відповідь

1. $\left[ \begin{array} { c c | c } { 1} & {2} &{ 3 } \\ { 4}&{5} &{ 6 } \end{array} \right]$

3. $\left[ \begin{array} { c c | c} { 1} &{ - 2} &{ 1 } \\ { 2} &{ - 1} &{ 1 } \end{array} \right]$

5. $\left[ \begin{array} { c c | c } { - 1} &{8} &{ 3 } \\ { 0} & {2} &{ 2 } \end{array} \right]$

7. $\left[ \begin{array} { c c c | c} { 3 } & { - 2 } & { 7 } & { 8 } \\ { 4} &{ - 5 } & { - 10 } & { 6 } \\ { - 1 } & { - 3 } & { 2 } & { - 1 } \end{array} \right]$

9. $\left[ \begin{array} { c c c | c } { 1 } & { - 9} &{5} &{ - 3 } \\ { 0 } & { 2} &{0 } & { 10 } \\ { 0 } & { 0} &{3 } & { 27 } \end{array} \right]$

11. $\left[ \begin{array} { c c c | c } { 8 } & { 2 } & { 0 } &{ - 13 } \\ { 0 } & { - 2 } & { 1 } & { 1 } \\ { 12 } & { 0 } & { - 5 } & { - 18 } \end{array} \right]$

Вправа$\PageIndex{6}$

Вирішити за допомогою матриць і гауссова елімінації.

1. $\left\{ \begin{array} { l } { x - 5 y = 2 } \\ { 2 x - y = 1 } \end{array} \right.$
2. $\left\{ \begin{array} { c } { x - 2 y = - 1 } \\ { x + y = 1 } \end{array} \right.$
3. $\left\{ \begin{array} { l } { 10 x - 7 y = 15 } \\ { - 2 x + 3 y = - 3 } \end{array} \right.$
4. $\left\{ \begin{array} { c } { 9 x - 10 y = 2 } \\ { 3 x + 5 y = - 1 } \end{array} \right.$
5. $\left\{ \begin{array} { l } { 3 x + 5 y = 8 } \\ { 2 x - 3 y = 18 } \end{array} \right.$
6. $\left\{ \begin{array} { l } { 5 x - 3 y = - 14 } \\ { 7 x + 2 y = - 1 } \end{array} \right.$
7. $\left\{ \begin{array} { c } { 9 x + 15 y = 5 } \\ { 3 x + 5 y = 7 } \end{array} \right.$
8. $\left\{ \begin{array} { c } { 6 x - 8 y = 1 } \\ { - 3 x + 4 y = - 1 } \end{array} \right.$
9. $\left\{ \begin{array} { l } { x + y = 0 } \\ { x - y = 0 } \end{array} \right.$
10. $\left\{ \begin{array} { l } { 7 x - 3 y = 0 } \\ { 3 x - 7 y = 0 } \end{array} \right.$
11. $\left\{ \begin{array} { c } { 2 x - 3 y = 4 } \\ { - 10 x + 15 y = - 20 } \end{array} \right.$
12. $\left\{ \begin{array} { l } { 6 x - 10 y = 20 } \\ { - 3 x + 5 y = - 10 } \end{array} \right.$
13. $\left\{ \begin{array} { l } { x + y - 2 z = - 1 } \\ { - x + 2 y - z = 1 } \\ { x - y + z = 2 } \end{array} \right.$
14. $\left\{ \begin{array} { c } { x - y + z = - 2 } \\ { x + 2 y - z = 6 } \\ { - x + y - 2 z = 3 } \end{array} \right.$
15. $\left\{ \begin{aligned} 2 x - y + z & = 2 \\ x - y + z & = 2 \\ - 2 x + 2 y - z & = - 1 \end{aligned} \right.$
16. $\left\{ \begin{array} { l } { 3 x - y + 2 z = 7 } \\ { - x + 2 y + z = 6 } \\ { x + 3 y - 2 z = 1 } \end{array} \right.$
17. $\left\{ \begin{aligned} x - 3 y + z & = 6 \\ - x - y + 2 z & = 4 \\ 2 x + y + z & = 3 \end{aligned} \right.$
18. $\left\{ \begin{aligned} 4 x - y + 2 z & = 12 \\ x - 3 y + 2 z & = 7 \\ - 2 x + 3 y + 4 z & = - 16 \end{aligned} \right.$
19. $\left\{ \begin{array} { c } { 2 x - 4 y + 6 z = - 4 } \\ { 3 x - 2 y + 5 z = - 2 } \\ { 5 x - y + 2 z = 1 } \end{array} \right.$
20. $\left\{ \begin{aligned} 3 x + 6 y + 9 z & = 6 \\ 2 x - 2 y + 3 z & = 0 \\ - 3 x + 18 y - 12 z & = 5 \end{aligned} \right.$
21. $\left\{ \begin{array} { l } { - x + y - z = - 2 } \\ { 3 x - 2 y + 5 z = 1 } \\ { 3 x - 5 y - z = 3 } \end{array} \right.$
22. $\left\{ \begin{array} { c } { x + 2 y + 3 z = 4 } \\ { 3 x + 8 y + 13 z = 21 } \\ { 2 x + 5 y + 8 z = 16 } \end{array} \right.$
23. $\left\{ \begin{array} { c } { 2 x - 4 y - 5 z = 3 } \\ { - x + y + z = 1 } \\ { 3 x - 4 y - 5 z = - 4 } \end{array} \right.$
24. $\left\{ \begin{array} { l } { 5 x - 3 y - 2 z = 4 } \\ { 3 x - 6 y + 4 z = - 6 } \\ { - x + 2 y - z = 2 } \end{array} \right.$
25. $\left\{ \begin{array} { c } { - 2 x - 3 y + 12 z = 4 } \\ { 4 x - 5 y - 10 z = - 1 } \\ { - x - 3 y + 2 z = 0 } \end{array} \right.$
26. $\left\{ \begin{array} { c } { 3 x - 2 y + 5 z = 10 } \\ { 4 x + 3 y - 3 z = - 6 } \\ { x + y + z = 2 } \end{array} \right.$
27. $\left\{ \begin{array} { c } { x + 2 y + z = - 3 } \\ { x + 6 y + 3 z = 7 } \\ { x + 4 y + 2 z = 2 } \end{array} \right.$
28. $\left\{ \begin{array} { c } { 2 x - y + z = 1 } \\ { 4 x - y + 3 z = 5 } \\ { 2 x + y + 3 z = 7 } \end{array} \right.$
29. $\left\{ \begin{array} { l } { 2 x + 3 y - 4 z = 0 } \\ { 3 x - 5 y + 3 z = - 10 } \\ { 5 x - 2 y + 5 z = - 4 } \end{array} \right.$
30. $\left\{ \begin{array} { l } { 3 x - 2 y + 9 z = 2 } \\ { - 2 x - 5 y - 4 z = 3 } \\ { 5 x - 3 y + 3 z = 15 } \end{array} \right.$
31. $\left\{ \begin{array} { l } { 8 x + 2 y = - 13 } \\ { - 2 y + z = 1 } \\ { 12 x - 5 z = - 18 } \end{array} \right.$
32. $\left\{ \begin{array} { l } { x - 3 z = 2 } \\ { y + 6 z = 4 } \\ { 2 x + 3 y = 12 } \end{array} \right.$
33. $\left\{ \begin{aligned} 9 x + 3 y - 11 z & = 6 \\ 2 x + y - 3 z & = 1 \\ 7 x + 2 y - 8 z & = 3 \end{aligned} \right.$
34. $\left\{ \begin{array} { c } { 3 x - y - z = 4 } \\ { - 5 x + y + 2 z = - 3 } \\ { 6 x - 2 y - 2 z = 8 } \end{array} \right.$
35. $\left\{ \begin{array} { l } { 2 x - 4 y + 3 z = 15 } \\ { 3 x - 5 y + 2 z = 18 } \\ { 5 x + 2 y - 6 z = 0 } \end{array} \right.$
36. $\left\{ \begin{array} { l } { 3 x - 4 y - 3 z = - 14 } \\ { 4 x + 2 y + 5 z = 12 } \\ { - 5 x + 8 y - 4 z = - 3 } \end{array} \right.$

Відповідь

1. $\left( \frac { 1 } { 3 } , - \frac { 1 } { 3 } \right)$

3. $\left( \frac { 3 } { 2 } , 0 \right)$

5. $( 6 , - 2 )$

7. $\varnothing$

9. $(0,0)$

11. $\left( x , \frac { 2 } { 3 } x - \frac { 4 } { 3 } \right)$

13. $(2, 3, 3)$

15. $(0, 1, 3)$

17. $(1, -1, 2)$

19. $(\left( \frac { 1 } { 2 } , \frac { 1 } { 2 } , - \frac { 1 } { 2 } \right)$

21. $\varnothing$

23. $(-7, -13, 7)$

25. $(1, 0, \frac{1}{2})$

27. $\left( - 8 , - \frac { 1 } { 2 } z + \frac { 5 } { 2 } , z \right)$

29. $(-1, 2, 1)$

31. $\left( - \frac { 3 } { 2 } , - \frac { 1 } { 2 } , 0 \right)$

33. $\varnothing$

35. $(2, -2, 1)$

Вправа$\PageIndex{7}$

1. Досліджуйте та обговоріть історію гаусової ліквідації. Кому зараховують перший розвиток цього процесу? Опублікуйте щось, що вам здалося цікавим, пов'язане з цією історією.
2. Дослідити та обговорити історію сучасних матричних позначень. Кому зараховується розробка? У яких сферах вони використовуються сьогодні? Опублікуйте свої висновки на дошці обговорень.

Відповідь

1. Відповідь може відрізнятися

Виноски

²² Лінійна система, що складається з рівнянь з трьома змінними в стандартній формі, розташованої так, що$x$ змінна не з'являється після першого рівняння, а$y$ змінна не з'являється після другого рівняння.

²³ Прямокутний масив чисел, що складається з рядків і стовпців.

²⁴ Матриця коефіцієнтів лінійної системи в стандартному вигляді записується, як вони виглядають вишикувалися без змінних або операцій.

²⁵ Матриця коефіцієнта з включеним стовпцем констант.

²⁶ Операції, які можуть бути виконані для отримання еквівалентних лінійних систем.

²⁷ Кроки, що використовуються для отримання еквівалентної лінійної системи у верхній трикутній формі, щоб її можна було вирішити за допомогою зворотної заміни.

²⁸ Матриця в трикутній формі, де провідний ненульовий елемент кожного рядка дорівнює 1