2.4: Графік основних функцій

Цілі навчання

• Визначте і пографуйте сім основних функцій.
• Визначте і графуйте кусково функції.
• Оцініть кусково визначені функції.
• Визначте найбільшу цілу функцію.

Основні функції

У цьому розділі ми графуємо сім основних функцій, які будуть використовуватися протягом цього курсу. Кожна функція графічна шляхом побудови точок. Пам'ятайте, що$f (x) = y$$f (x)$ і таким чином і$y$ можна використовувати взаємозамінно.

Будь-яка функція виду$f (x) = c$, де$c$ знаходиться будь-яке дійсне число, називається постійною функцією ⁴³. Постійні функції лінійні і можуть бути записані$f (x) = 0x + c$. У такому вигляді зрозуміло, що нахил є$0$ і$y$ -перехоплення є$(0, c)$. Оцінка будь-якого значення для$x$, наприклад$x = 2$, призведе до$c$.

Малюнок$\PageIndex{1}$

Графік постійної функції - горизонтальна лінія. Домен складається з усіх дійсних чисел,$ℝ$ а діапазон складається з одного значення$\{c\}$.

Далі визначаємо функцію ідентичності ⁴⁴$f (x) = x$. Оцінка будь-якого значення для$x$ призведе до того ж значення. Наприклад,$f (0) = 0$ і$f (2) = 2$. Функція ідентичності лінійна$f (x) = 1x + 0$, з нахилом$m = 1$ і$y$ -перехопленням$(0, 0)$.

Малюнок$\PageIndex{2}$

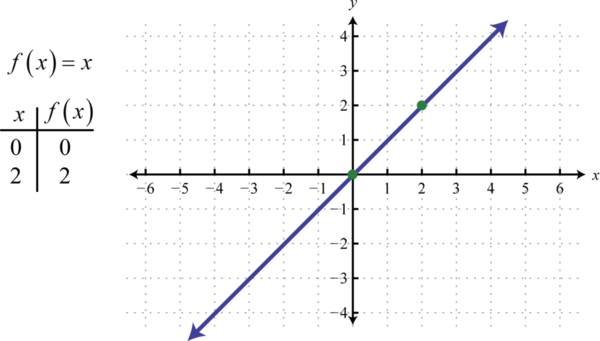
Домен і діапазон складаються з усіх дійсних чисел.

Квадратна функція ⁴⁵, визначена$f (x) = x^{2}$, - це функція, отримана шляхом зведення в квадрат значень в області. Наприклад,$f (2) = (2)^{2} = 4$ і$f (−2) = (−2)^{2} = 4$ .Результат зведення в квадрат ненульових значень в області завжди буде позитивним.

Малюнок$\PageIndex{3}$

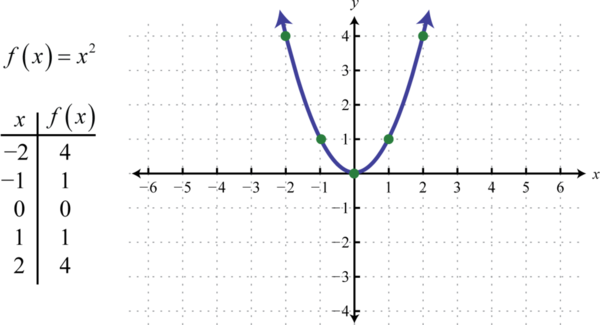
Отриманий вигнутий графік називається параболою ⁴⁶. Домен складається з усіх дійсних чисел,$ℝ$ а діапазон складається з усіх$y$ -значень, більших або рівних нулю$[0, ∞)$.

Функція кубінгу ⁴⁷,$f (x) = x^{3}$ визначена, піднімає всі значення в області до третьої степені. Результати можуть бути як позитивними, так і нульовими, або негативними. Наприклад$f (1) = (1)^{3} = 1, f (0) = (0)^{3} = 0$, і$f (−1) = (−1)^{3} = −1$.

Малюнок$\PageIndex{4}$

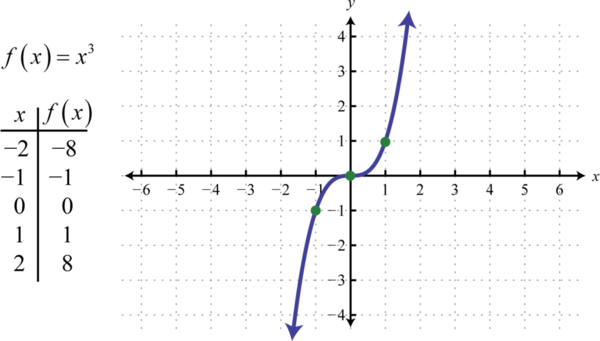
Домен і діапазон складаються з усіх дійсних чисел$ℝ$.

Зауважте, що функції константи, ідентичності, квадратури та кубінгу є прикладами основних поліноміальних функцій. Наступні три основні функції не є поліномами.

Функція абсолютного значення ⁴⁸, визначена$f (x) = |x|$, є функцією, де вихід представляє відстань до початку на числовому рядку. Результат оцінювання функції абсолютного значення для будь-якого ненульового значення завжди$x$ буде додатним. Наприклад,$f (−2) = |−2| = 2$ і$f (2) = |2| = 2$.

Малюнок$\PageIndex{5}$

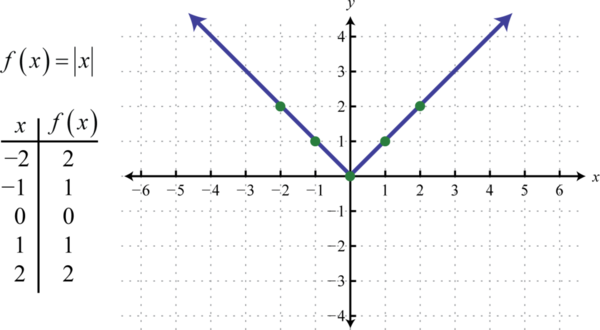
Область функції абсолютного значення складається з усіх дійсних чисел,$ℝ$ а діапазон складається з усіх$y$ -значень, більших або рівних нулю$[0, ∞)$.

Функція квадратного кореня ⁴⁹$f (x) = \sqrt{x}$, визначена, не визначається як дійсне число, якщо$x$ -значення від'ємні. Тому найменше значення в домені дорівнює нулю. Наприклад,$f (0) = \sqrt{0}= 0$ і$f (4) = \sqrt{4}= 2$.

Малюнок$\PageIndex{6}$

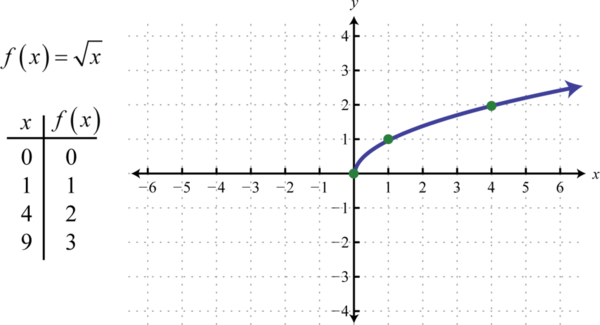
Домен і діапазон складаються з дійсних чисел, більших або рівних нулю$[0, ∞)$.

Зворотна функція ⁵⁰, визначена$f (x) = \frac{1}{x}$, є раціональною функцією з одним обмеженням на область, а саме$x ≠ 0$. Зворотне$x$ значення -значення, дуже близьке до нуля, дуже велике. Наприклад,

$\begin{aligned} f ( 1 / 10 ) &= \frac { 1 } { \left( \frac { 1 } { 10 } \right) } = 1 \cdot \frac { 10 } { 1 } = 10 \\ f ( 1 / 100 ) &= \frac { 1 } { \left( \frac { 1 } { 100 } \right) } = 1 \cdot \frac { 100 } { 1 } = 100 \\ f ( 1 / 1,000 )& = \frac { 1 } { \left( \frac { 1 } { 1,000 } \right) } = 1 \cdot \frac { 1,000 } { 1 } = 1,000 \end{aligned}$

Іншими словами, коли$x$ -значення наближаються до нуля, їх взаємні будуть прагнути або до позитивної, або негативної нескінченності. Це описує вертикальну асимптоту ⁵¹ на$y$ -осі. Крім того, де$x$ -значення дуже великі, результат зворотної функції дуже малий.

$\begin{aligned} f ( 10 ) & = \frac { 1 } { 10 } = 0.1 \\ f ( 100 ) & = \frac { 1 } { 100 } = 0.01 \\ f ( 1000 ) & = \frac { 1 } { 1,000 } = 0.001 \end{aligned}$

Іншими словами, оскільки$x$ -значення стають дуже великими, результуючі$y$ -значення прагнуть до нуля. Це описує горизонтальну асимптоту ⁵² на$x$ -осі. Після побудови ряду точок можна визначити загальну форму зворотної функції.

Малюнок$\PageIndex{7}$

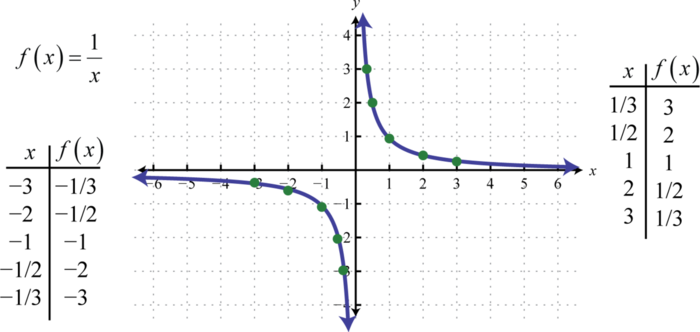
І область, і діапазон зворотної функції складається з усіх дійсних чисел$0$, крім, які можуть бути виражені за допомогою інтервальних позначень наступним чином:$(−∞, 0) ∪ (0, ∞)$.

Підсумовуючи, основними поліноміальними функціями є:

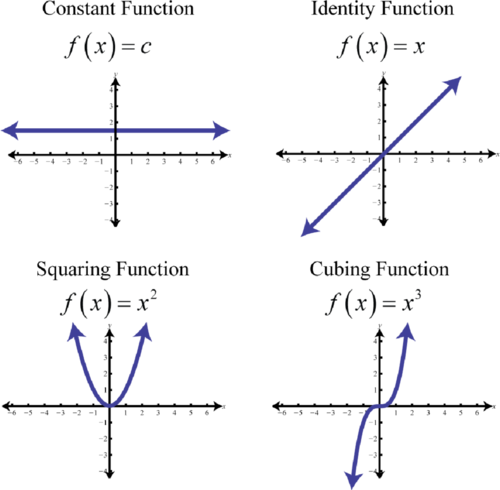
Малюнок$\PageIndex{8}$

Основними неполіноміальними функціями є:

Малюнок$\PageIndex{9}$

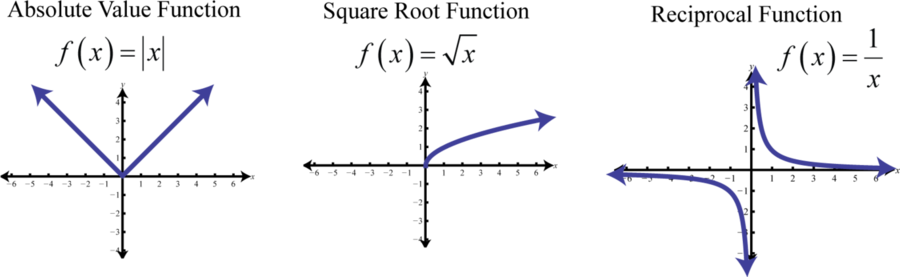
Кусково визначені функції

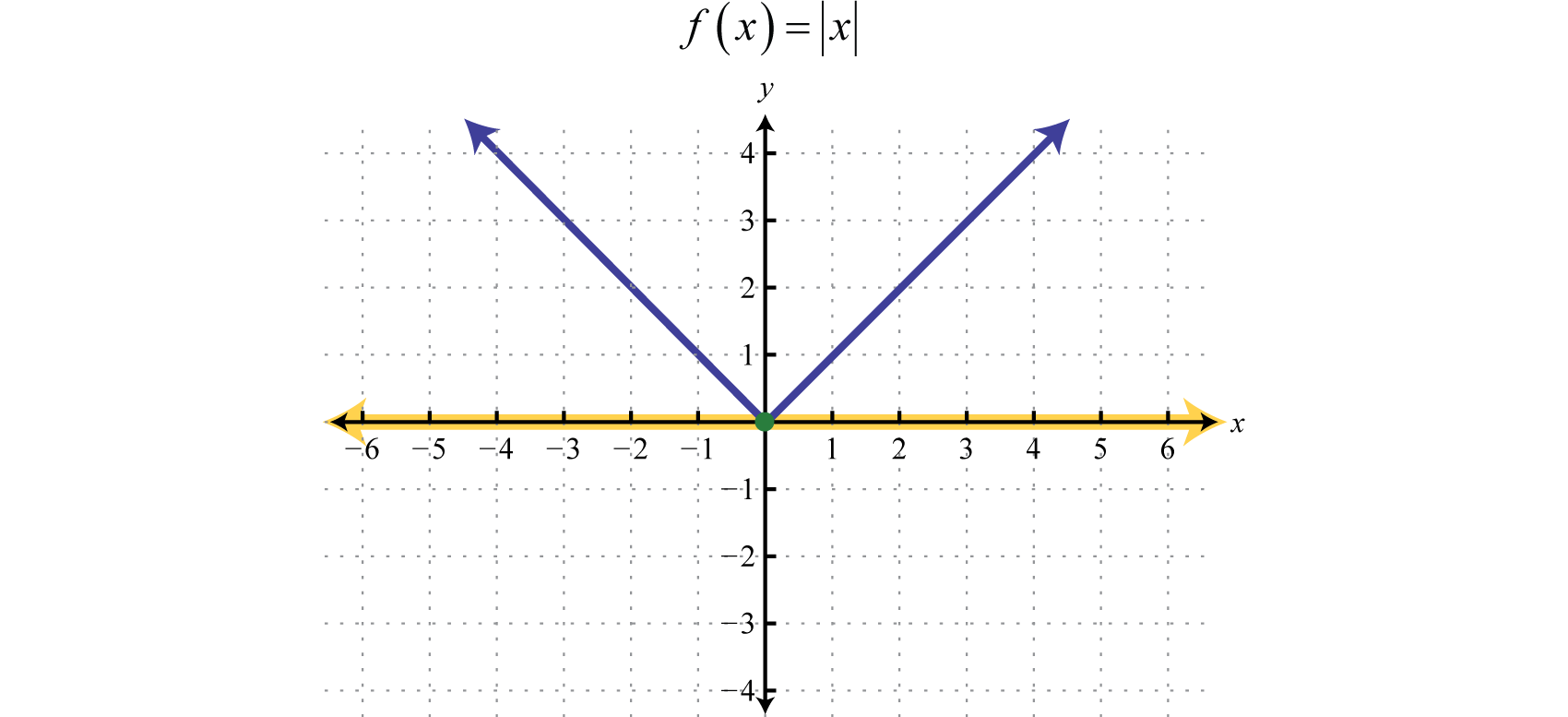
Кускова функція ⁵³, або функція спліт ⁵⁴, - це функція, визначення якої змінюється залежно від значення в області. Наприклад, ми можемо записати функцію абсолютного значення$f(x) = |x|$ як кускову функцію:

$f ( x ) = | x | = \left\{ \begin{array} { c l } { x } & { \text { if } x \geq 0 } \\ { - x } & { \text { if } x < 0 } \end{array} \right.$

В даному випадку використовуване визначення залежить від знака$x$ -значення. Якщо$x$ -value позитивне$x ≥ 0$, то функція визначається за допомогою$f(x) = x$. І якщо$x$ -значення$x < 0$ від'ємне, то функція визначається$f(x) = −x$.

Малюнок$\PageIndex{10}$

Далі наведено графік двох частин на одній прямокутній координатній площині:

Малюнок$\PageIndex{11}$

Приклад$\PageIndex{1}$:

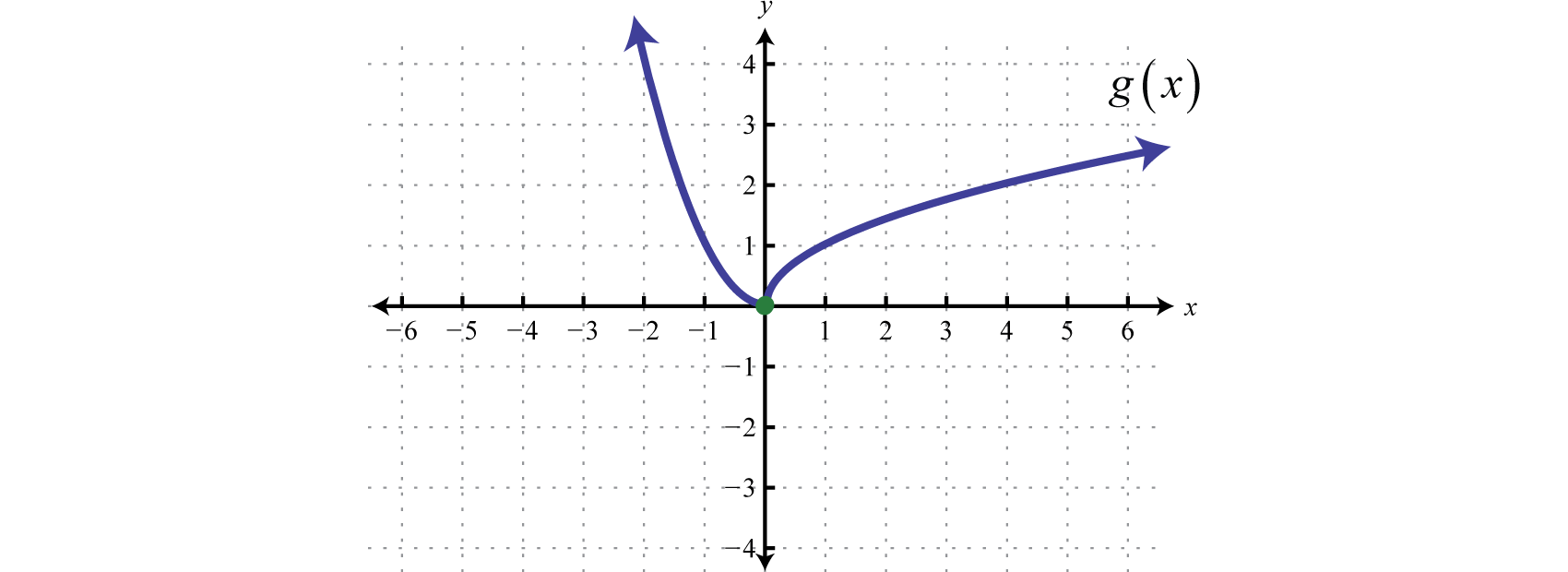
Графік:$g ( x ) = \left\{ \begin{array} { c c c } { x ^ { 2 } } & { \text { if } } & { x < 0 } \\ { \sqrt { x } } & { \text { if } } & { x \geq 0 } \end{array} \right.$.

Рішення

У цьому випадку ми графуємо функцію квадрата над негативними$x$ -значеннями та функцію квадратного кореня над додатними$x$ -значеннями.

Малюнок$\PageIndex{12}$

Зверніть увагу на відкриту точку, яка використовується в початковій точці для функції квадратування, і замкнуту крапку, яка використовується для функції квадратного кореня. Це визначалося нерівністю, яка визначає область кожного фрагмента функції. Вся функція складається з кожного фрагмента, розміщеного на одній координатній площині.

Відповідь:

Малюнок$\PageIndex{13}$

При оцінці значення в області визначає відповідне визначення для використання.

Приклад$\PageIndex{2}$:

З огляду на функцію$h$, знайдіть$h(−5), h(0),$ і$h(3)$.

Рішення

Використовувати$h(t) = 7t + 3$ де$t$ негативний, як зазначено$t < 0$.

$\begin{aligned} h ( t ) & = 7 t + 5 \\ h ( \color{Cerulean}{- 5}\color{Black}{ )} & = 7 ( \color{Cerulean}{- 5}\color{Black}{)} + 3 \\ & = - 35 + 3 \\ & = - 32 \end{aligned}$

Де$t$ більше або дорівнює нулю, використовуйте$h(t) = −16t^{2} + 32t$.

$\begin{aligned} h ( \color{Cerulean}{0}\color{Black}{ )} & = - 16 ( \color{Cerulean}{0}\color{Black}{ )} + 32 ( \color{Cerulean}{0}\color{Black}{ )} h ( \color{Cerulean}{3}\color{Black}{ )} = 16 ( \color{Cerulean}{3}\color{Black}{ )} ^ { 2 } + 32 ( \color{Cerulean}{3}\color{Black}{ )} \\ & = 0 + 0 \quad\quad\quad\quad\quad\:\quad = -144 +96 \\ & = 0 \quad\quad\quad\quad\quad\quad\quad\quad = - 48 \end{aligned}$

Відповідь:

$h(−5) = −32, h(0) = 0,$і$h(3) = −48$

Вправа$\PageIndex{1}$

Графік:$f ( x ) = \left\{ \begin{array} { l l } { \frac { 2 } { 3 } x + 1 } & { \text { if } x < 0 } \\ { x ^ { 2 } } & { \text { if } x \geq 0 } \end{array} \right.$.

Відповідь

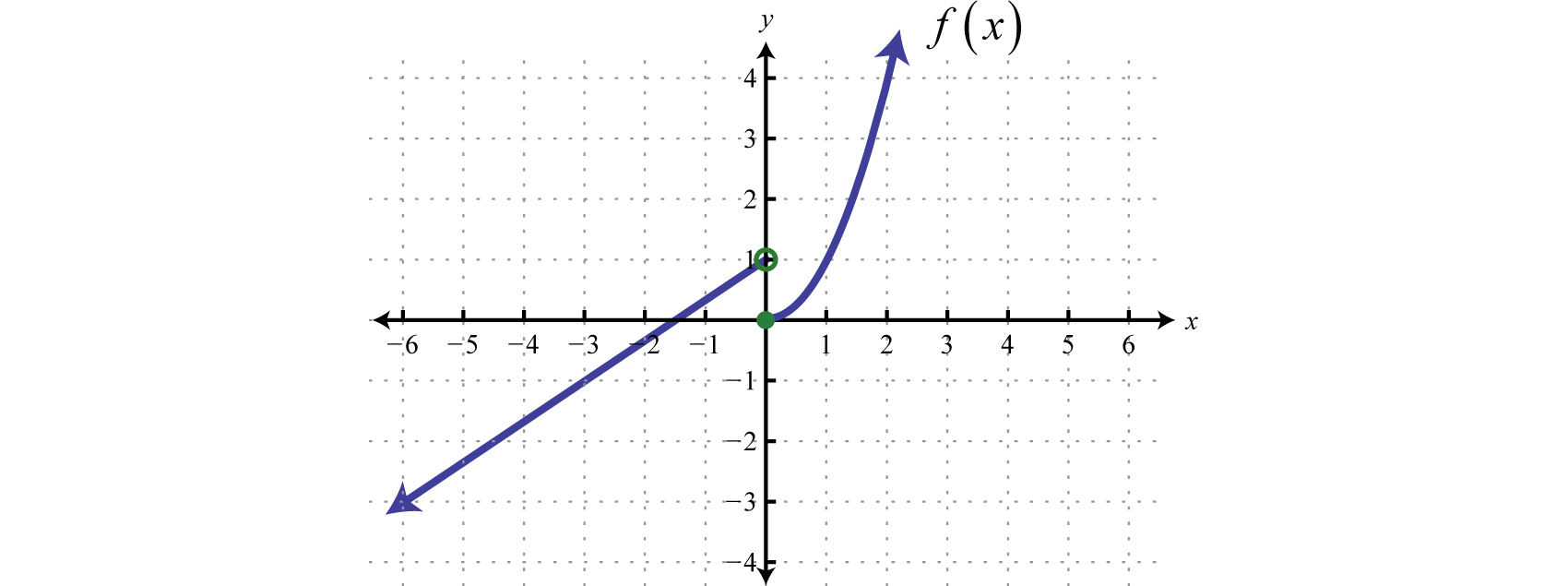
Малюнок$\PageIndex{14}$

www.youtube.com/В/0 ПриємнийN5BLW

Визначення функції може відрізнятися протягом декількох інтервалів в області.

Приклад$\PageIndex{3}$:

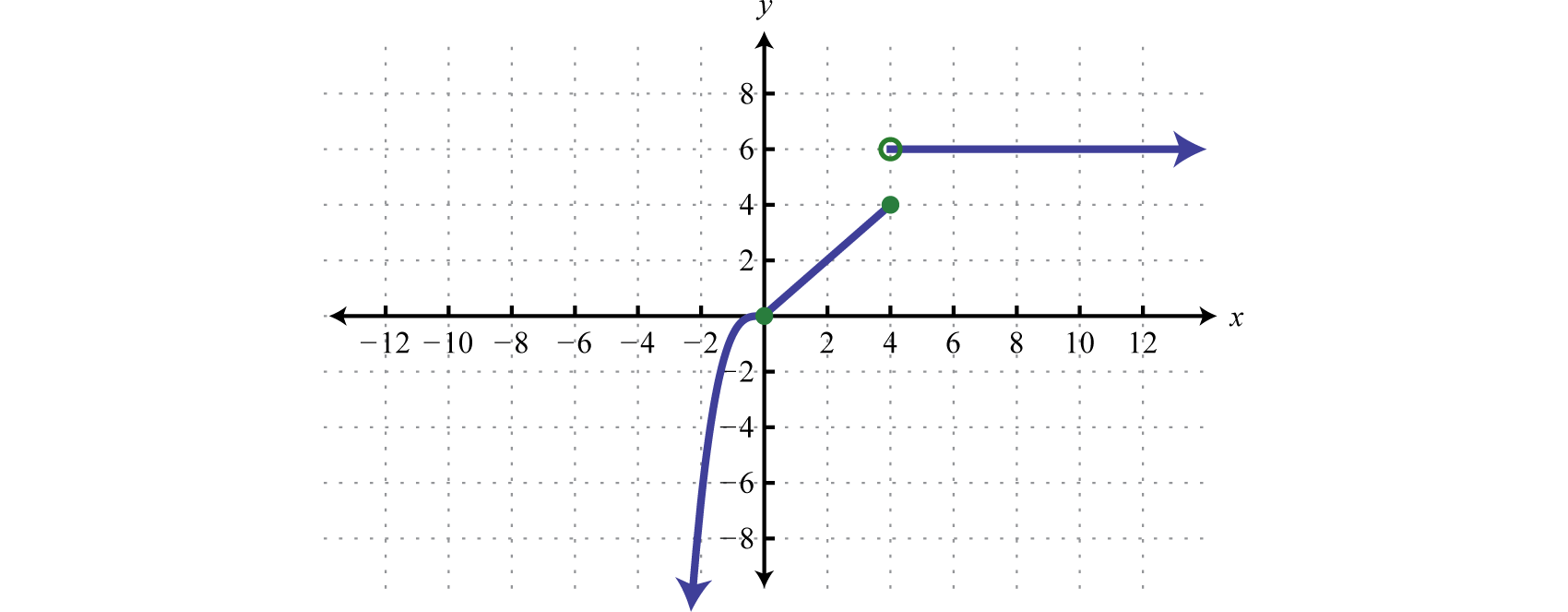
Графік:$f ( x ) = \left\{ \begin{array} { l l } { x ^ { 3 } } & { \text { if } x < 0 } \\ { x } & { \text { if } 0 \leq x \leq 4 } \\ { 6 } & { \text { if } x > 4 } \end{array} \right.$.

Рішення

У цьому випадку графуйте функцію кубінга протягом інтервалу$(−∞,0)$. Графік функції ідентичності протягом інтервалу$[0,4]$. Нарешті, графік постійної функції$f(x)=6$ протягом інтервалу$(4,∞)$. І тому, що$f(x)=6$ де$x>4$, ми використовуємо відкриту точку в точці$(4,6)$. Де$x=4$, ми використовуємо$f(x)=x$ і таким чином$(4,4)$ знаходиться точка на графіку, як зазначено замкнутою крапкою.

Відповідь:

Малюнок$\PageIndex{15}$

Найбільша ціла функція ⁵⁵, що позначається$f(x) = \left[\!\![x]\!\!\right]$, привласнює найбільше ціле число менше або рівне будь-якому дійсному числу в своїй області. Наприклад,

$\begin{aligned} f ( 2.7 ) & = \left[\!\![2.7]\!\!\right] = 2 \\ f ( \pi ) & = \left[\!\![\pi]\!\!\right] = 3 \\ f ( 0.23 ) & = \left[\!\![0.23]\!\!\right] = 0 \\ f ( - 3.5 ) & = \left[\!\![-3.5]\!\!\right] = - 4 \end{aligned}$

Ця функція пов'язує будь-яке дійсне число з найбільшим цілим числом менше або рівним йому і не слід плутати з округленням.

Приклад$\PageIndex{4}$:

Графік:$f(x) = \left[\!\![x]\!\!\right]$.

Рішення

Якщо$x$ є будь-яким дійсним числом, то$y = \left[\!\![x]\!\!\right]$ є найбільшим цілим числом менше або дорівнює$x$.

$\begin{aligned} \vdots\\- 1 \leq x < 0 & \color{Cerulean}{\Rightarrow}\color{Black}{ y} = \left[\!\![x]\!\!\right] = -1 \\ 0 \leq x < 1 & \color{Cerulean}{\Rightarrow} \color{Black}{y} = \left[\!\![x]\!\!\right] = 0 \\ 1 \leq x < 2 & \color{Cerulean}{\Rightarrow}\color{Black}{ y} = \left[\!\![x]\!\!\right] = 1 \\ & \vdots \end{aligned}$

Використовуючи це, отримаємо наступний графік.

Відповідь:

Малюнок$\PageIndex{16}$

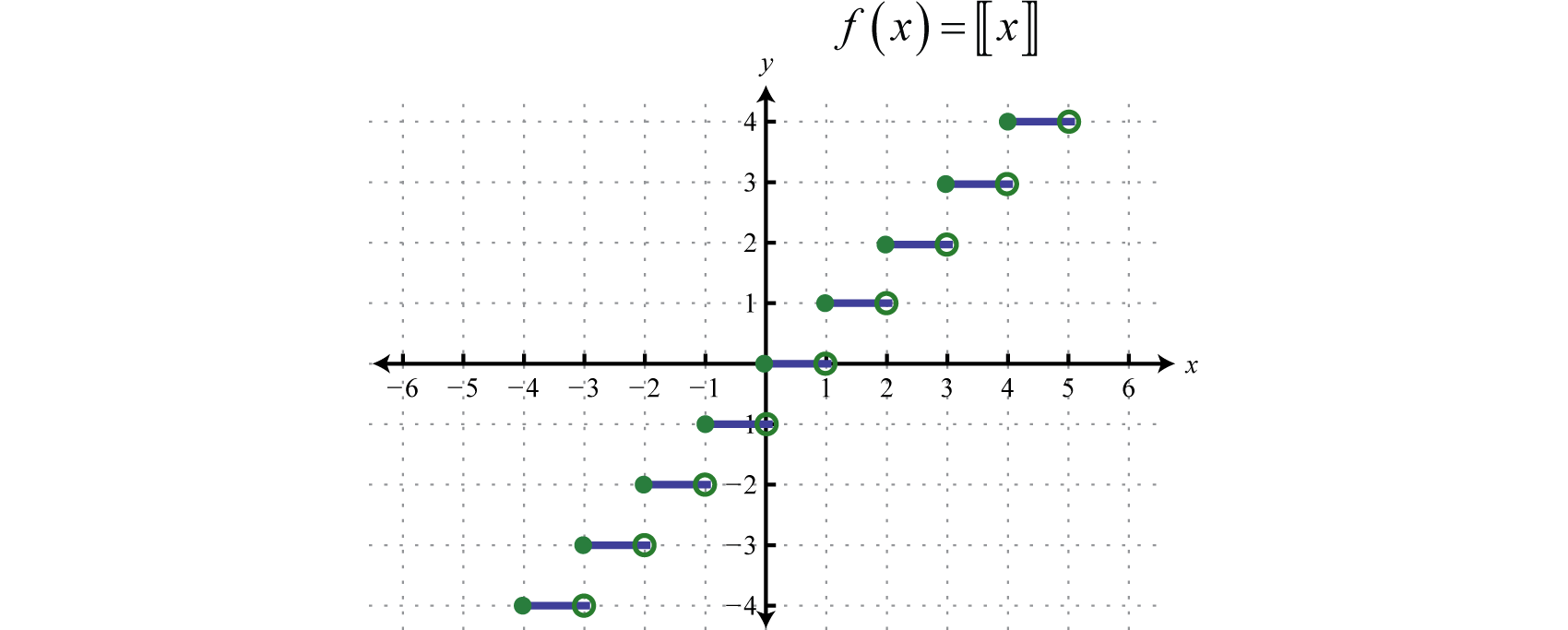
Область найбільшої цілої функції складається з усіх дійсних чисел,$\mathbb{R}$ а діапазон складається з безлічі цілих чисел$\mathbb{Z}$. Цю функцію часто називають функцією підлоги ⁵⁶ і має безліч застосувань в інформатиці.

Ключові винос

• Ділянка точок для визначення загальної форми основних функцій. Форма, а також область і діапазон кожного повинні бути запам'ятовані.
• Основними поліноміальними функціями є:$f(x) = c, f(x) = x , f(x) = x^{2}$, і$f(x) = x^{3}$.
• Основними неполіноміальними функціями є:$f(x) = |x|, f(x) = \sqrt{x}$, і$f(x) = \frac{1}{x}$.
• Функція, визначення якої змінюється в залежності від значення в області, називається кусковою функцією. Значення в домені визначає відповідне визначення для використання.

Вправа$\PageIndex{2}$

Зіставте графік з визначенням функції.

Малюнок$\PageIndex{17}$

Малюнок$\PageIndex{18}$

Малюнок$\PageIndex{19}$

Малюнок$\PageIndex{20}$

Малюнок$\PageIndex{21}$

Малюнок$\PageIndex{22}$

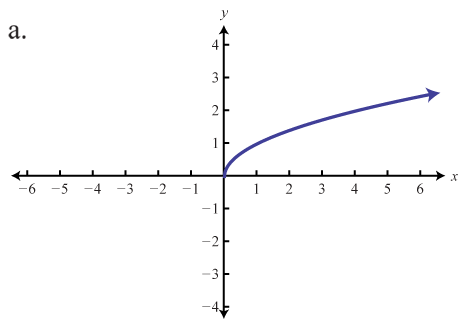
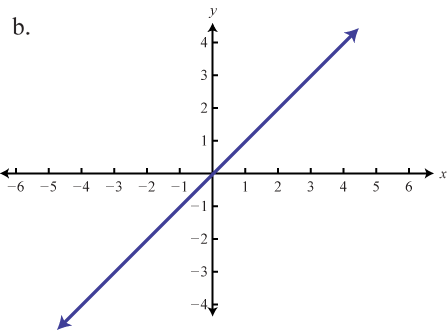
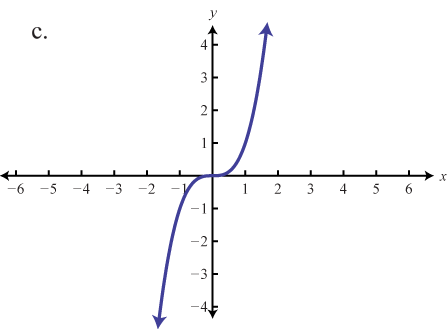
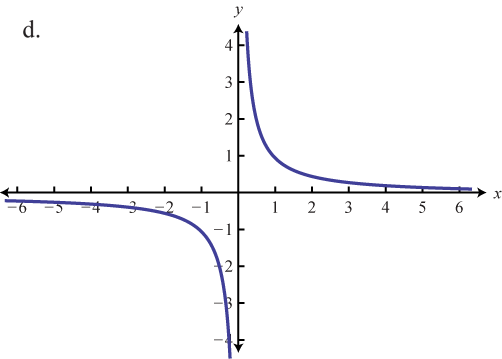
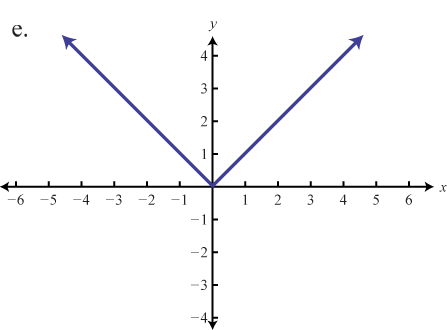
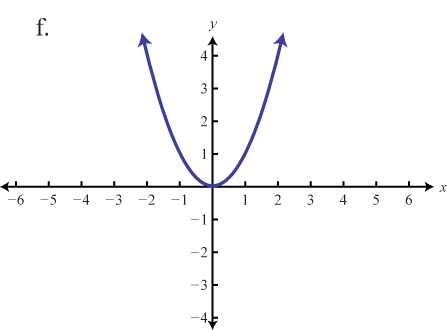
1. $f(x) = x$
2. $f(x) = x^{2}$
3. $f(x) = x^{3}$
4. $f(x) = |x|$
5. $f(x) = x$
6. $f(x) = \frac{1}{x}$

Відповідь

1. $b$

3. $c$

5. $a$

Вправа$\PageIndex{3}$

Оцінити.

1. $f(x) = x$; знайти$f(−10), f(0)$, і$f(a)$.
2. $f(x) = x^{2}$; знайти$f(−10), f(0)$, і$f(a)$.
3. $f(x) = x^{3}$; знайти$f(−10), f(0)$, і$f(a)$.
4. $f(x) = |x|$; знайти$f(−10), f(0)$, і$f(a)$.
5. $f(x) = \sqrt{x}$;$find f(25), f(0)$, і$f(a)$ де$a ≥ 0$.
6. $f(x) = \frac{1}{x}$; знайти$f(−10), f (\frac{1}{5})$, і$f(a)$ де$a ≠ 0$.
7. $f(x) = 5$; знайти$f(−10), f(0)$, і$f(a)$.
8. $f(x) = −12$; знайти$f(−12), f(0)$, і$f(a)$.
9. Графік$f(x) = 5$ і вказати його область і діапазон.
10. Графік$f(x) = −9$ та стан його області та діапазону

Відповідь

1. $f ( - 10 ) = - 10 , f ( 0 ) = 0 , f ( a ) = a$

3. $f ( - 10 ) = - 1,000 , f ( 0 ) = 0 , f ( a ) = a ^ { 3 }$

5. $f ( 25 ) = 5 , f ( 0 ) = 0 , f ( a ) = \sqrt { a }$

7. $f ( - 10 ) = 5 , f ( 0 ) = 5 , f ( a ) = 5$

9. Домен:$\mathbb{R}$; діапазон$\{5\}$

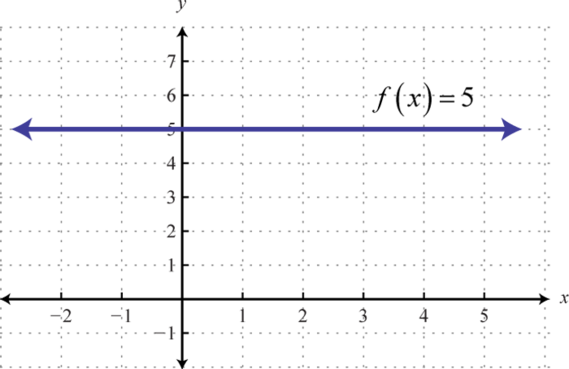
Малюнок$\PageIndex{23}$

Вправа$\PageIndex{4}$

Функція кореня куба.

1. 17. Знайти точки на графіку функції, визначеної$f ( x ) = \sqrt [ 3 ] { x }$ with$x$ -values у множині$\{−8, −1, 0, 1, 8\}$.
2. Знайти точки на графіку функції, визначеної$f ( x ) = \sqrt [ 3 ] { x }$ with$x$ -values у множині$\{−3, −2, 1, 2, 3\}$. Скористайтеся калькулятором і округляйте до найближчої десятої.
3. Графік функції кореня куба, визначену$f ( x ) = \sqrt [ 3 ] { x }$ шляхом побудови точок, знайдених у попередніх двох вправах.
4. Визначте область і діапазон функції кореня куба.

Відповідь

1. $\{ ( - 8 , - 2 ) , ( - 1 , - 1 ) , ( 0,0 ) , ( 1,1 ) , ( 8,2 ) \}$

3.

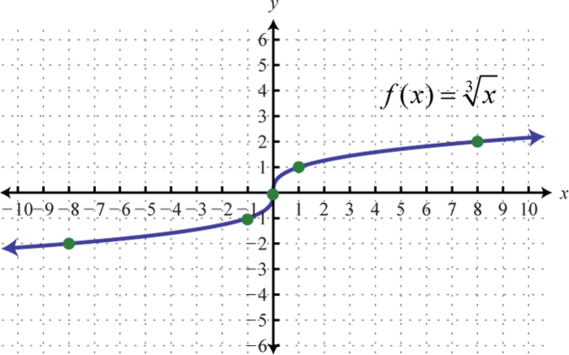
Малюнок$\PageIndex{24}$

Вправа$\PageIndex{5}$

Знайдіть впорядковану пару, яка вказує точку$P$.

1.

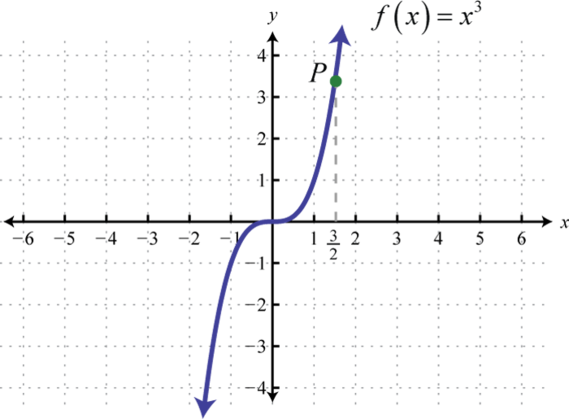
Малюнок$\PageIndex{25}$

2.

Малюнок$\PageIndex{26}$

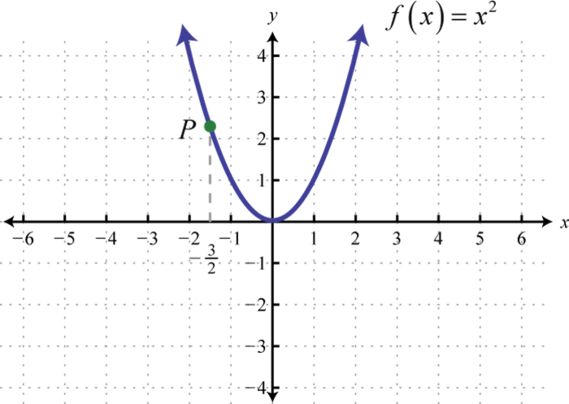
3.

Малюнок$\PageIndex{27}$

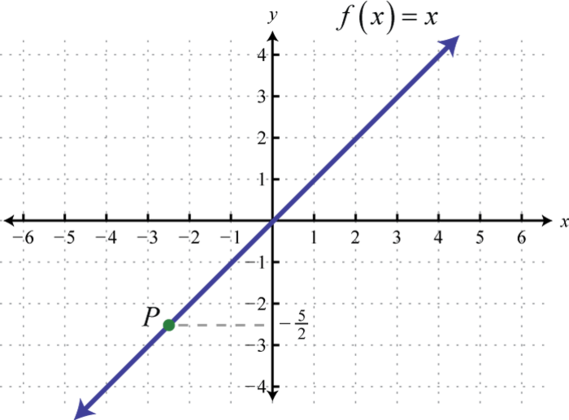
4.

Малюнок$\PageIndex{28}$

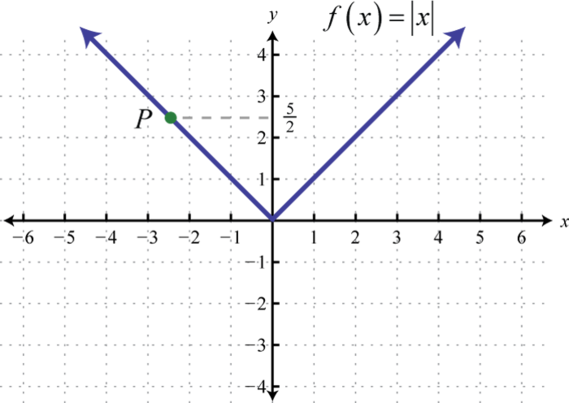
Відповідь

1. $\left( \frac { 3 } { 2 } , \frac { 27 } { 8 } \right)$

3. $\left( - \frac { 5 } { 2 } , - \frac { 5 } { 2 } \right)$

Вправа$\PageIndex{6}$

Графік кусково функцій.

1. $g ( x ) = \left\{ \begin{array} { l l } { 2 } & { \text { if } x < 0 } \\ { x } & { \text { if } x \geq 0 } \end{array} \right.$
2. $g ( x ) = \left\{ \begin{array} { l l } { x ^ { 2 } } & { \text { if } x < 0 } \\ { 3 } & { \text { if } x \geq 0 } \end{array} \right.$
3. $h ( x ) = \left\{ \begin{array} { l l } { x } & { \text { if } x < 0 } \\ { \sqrt { x } } & { \text { if } x \geq 0 } \end{array} \right.$
4. $h ( x ) = \left\{ \begin{array} { l } { | x | \text { if } x < 0 } \\ { x ^ { 3 } \text { if } x \geq 0 } \end{array} \right.$
5. $f ( x ) = \left\{ \begin{array} { l } { | x | \text { if } x < 2 } \\ { 4 \text { if } x \geq 2 } \end{array} \right.$
6. $f ( x ) = \left\{ \begin{array} { l l } { x } & { \text { if } x < 1 } \\ { \sqrt { x } } & { \text { if } x \geq 1 } \end{array} \right.$
7. $g ( x ) = \left\{ \begin{array} { l l } { x ^ { 2 } \text { if } x \leq - 1 } \\ { x \quad \text { if } x > - 1 } \end{array} \right.$
8. $g ( x ) = \left\{ \begin{array} { l } { - 3 \text { if } x \leq - 1 } \\ { x ^ { 3 } \text { if } x > - 1 } \end{array} \right.$
9. $h ( x ) = \left\{ \begin{array} { l } { 0 \text { if } x \leq 0 } \\ { \frac { 1 } { x } \text { if } x > 0 } \end{array} \right.$
10. $h ( x ) = \left\{ \begin{array} { l } { \frac { 1 } { x } \text { if } x < 0 } \\ { x ^ { 2 } \text { if } x \geq 0 } \end{array} \right.$
11. $f ( x ) = \left\{ \begin{array} { l l } { x ^ { 2 } } & { \text { if } x < 0 } \\ { x } & { \text { if } 0 \leq x < 2 } \\ { - 2 } & { \text { if } x \geq 2 } \end{array} \right.$
12. $f ( x ) = \left\{ \begin{array} { l l } { x } & { \text { if } x < - 1 } \\ { x ^ { 3 } } & { \text { if } - 1 \leq x < 1 } \\ { 3 } & { \text { if } x \geq 1 } \end{array} \right.$
13. $g ( x ) = \left\{ \begin{array} { l l } { 5 } & { \text { if } x < - 2 } \\ { x ^ { 2 } } & { \text { if } - 2 \leq x < 2 } \\ { x } & { \text { if } x \geq 2 } \end{array} \right.$
14. $g ( x ) = \left\{ \begin{array} { l l } { x } & { \text { if } x < - 3 } \\ { | x | } & { \text { if } - 3 \leq x < 1 } \\ { \sqrt { x } } & { \text { if } x \geq 1 } \end{array} \right.$
15. $h ( x ) = \left\{ \begin{array} { l } { \frac { 1 } { x } \text { if } x < 0 } \\ { x ^ { 2 } \text { if } 0 \leq x < 2 } \\ { 4 \text { if } x \geq 2 } \end{array} \right.$
16. $h ( x ) = \left\{ \begin{array} { l } { 0 \text { if } x < 0 } \\ { x ^ { 3 } \text { if } 0 < x \leq 2 } \\ { 8 \text { if } x > 2 } \end{array} \right.$
17. $f ( x ) = [\left[\!\![x+0.5]\!\!\right]$
18. $f(x) = \left[\!\![x]\!\!\right] +1$
19. $f(x) = \left[\!\![0.5x]\!\!\right]$
20. $f(x) = 2\left[\!\![x]\!\!\right]$

Відповідь

1.

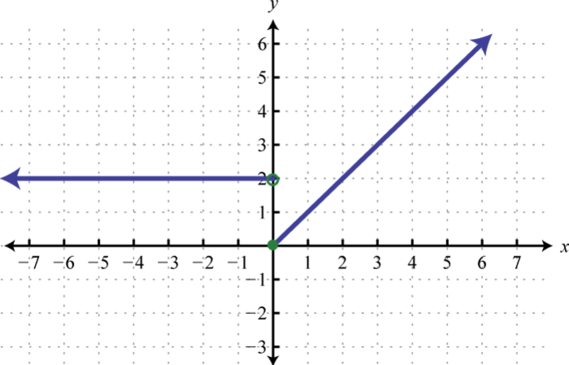
Малюнок$\PageIndex{29}$

3.

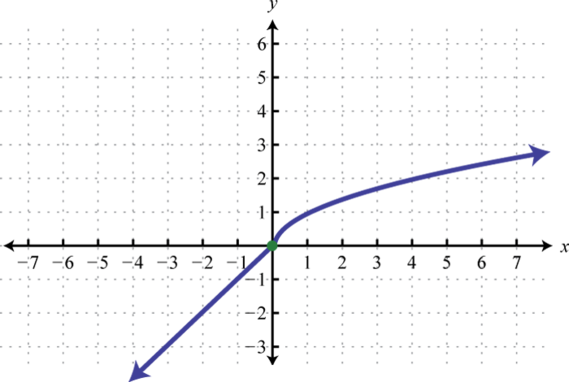
Малюнок$\PageIndex{50}$

5.

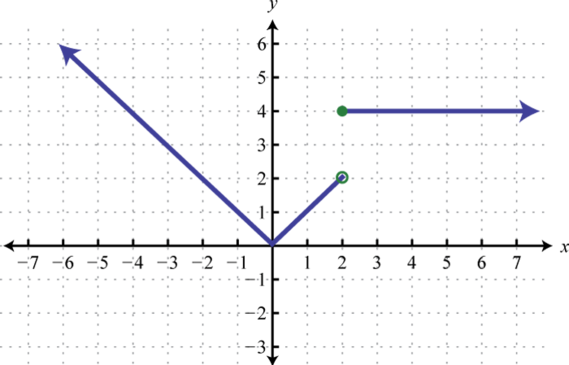
Малюнок$\PageIndex{51}$

7.

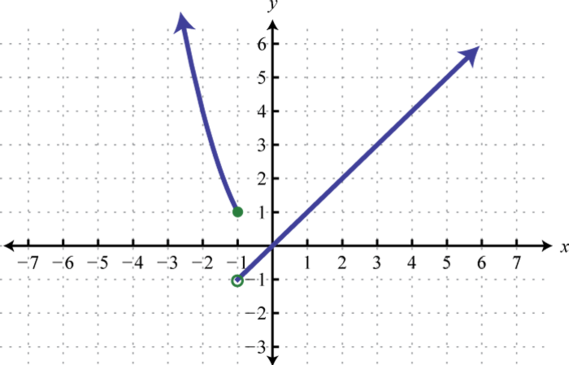
Малюнок$\PageIndex{52}$

9.

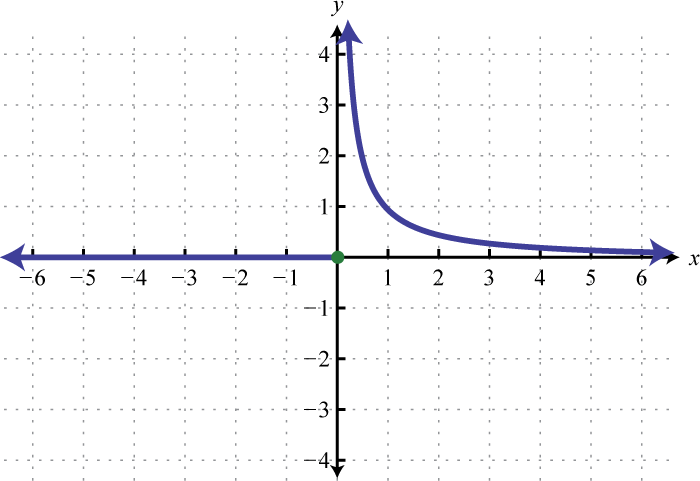
Малюнок$\PageIndex{53}$

11.

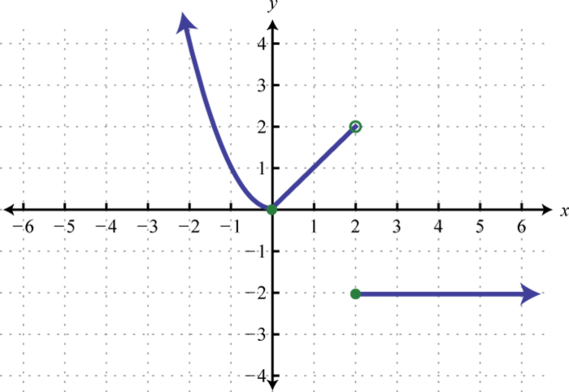
Малюнок$\PageIndex{54}$

13.

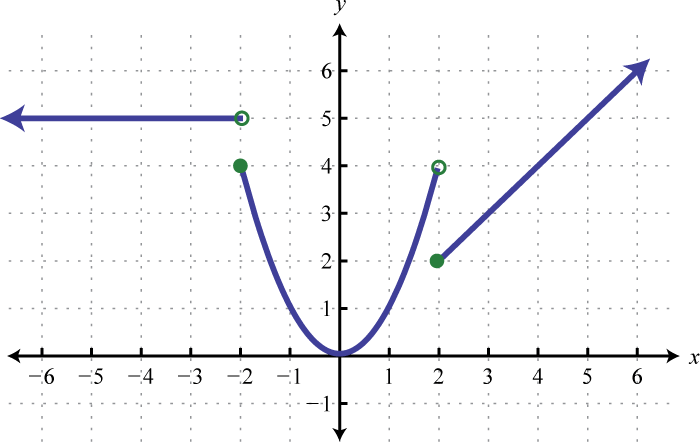
Малюнок$\PageIndex{55}$

15.

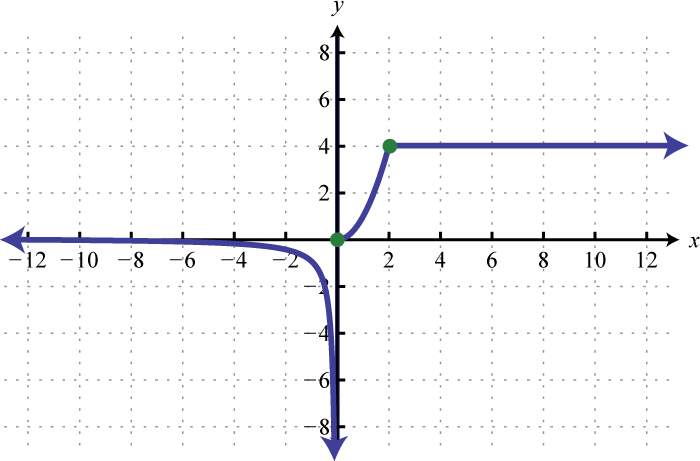
Малюнок$\PageIndex{56}$

17.

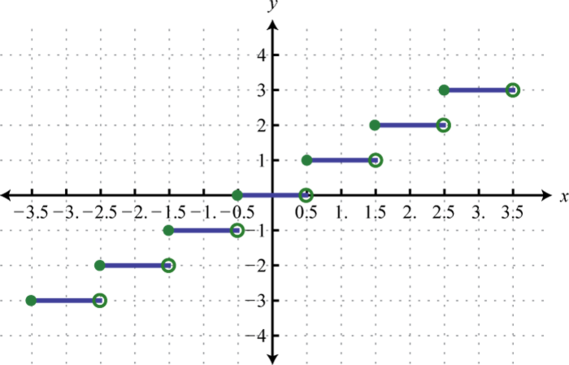
Малюнок$\PageIndex{57}$

19.

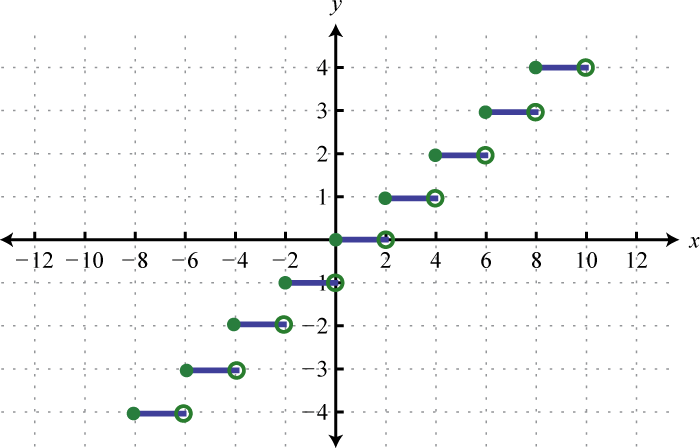
Малюнок$\PageIndex{58}$

Вправа$\PageIndex{7}$

Оцінити.

1. $f ( x ) = \left\{ \begin{array} { l l } { x ^ { 2 } } & { \text { if } x \leq 0 } \\ { x + 2 } & { \text { if } x > 0 } \end{array} \right.$

Знайти$f(-5), f(0)$, і$f(3)$.

2. $f ( x ) = \left\{ \begin{array} { l l } { x ^ { 3 } } & { \text { if } x < 0 } \\ { 2 x - 1 } & { \text { if } x \geq 0 } \end{array} \right.$

Знайти$f(−3), f(0)$, і$f(2)$.

3. $g ( x ) = \left\{ \begin{array} { l l } { 5 x - 2 } & { \text { if } x < 1 } \\ { \sqrt { x } } & { \text { if } x \geq 1 } \end{array} \right.$

Знайти$g(−1), g(1)$, і$g(4)$.

4. $g ( x ) = \left\{ \begin{array} { l } { x ^ { 3 } \text { if } x \leq - 2 } \\ { | x | \text { if } x > - 2 } \end{array} \right.$

Знайти$g(−3), g(−2)$, і$g(−1)$.

5. $h ( x ) = \left\{ \begin{array} { l l } { - 5 } & { \text { if } x < 0 } \\ { 2 x - 3 } & { \text { if } 0 \leq x < 2 } \\ { x ^ { 2 } } & { \text { if } x \geq 2 } \end{array} \right.$

Знайти$h(−2), h(0)$, і$h(4)$.

6. $h ( x ) = \left\{ \begin{array} { l } { - 3 x \text { if } x \leq 0 } \\ { x ^ { 3 } \text { if } 0 < x \leq 4 } \\ { \sqrt { x } \text { if } x > 4 } \end{array} \right.$

Знайти$h(−5), h(4)$, і$h(25)$.

7. $f ( x ) = \left[\!\![x-0.5]\!\!\right]$

Знайти$f(−2), f(0)$, і$f(3)$.

8. $f ( x ) = \left[\!\![2x]\!\!\right] + 1$

Знайти$f(−1.2), f(0.4)$, і$f(2.6)$.

Відповідь

1. $f (−5) = 25, f(0) = 0$, і$f(3) = 5$

3. $g(−1) = −7, g(1) = 1$, і$g(4) = 2$

5. $h(−2) = −5, h(0) = −3$, і$h(4) = 16$

7. $f(−2) = −3, f(0) = −1$, і$f(3) = 2$

Вправа$\PageIndex{8}$

Оцініть заданий графік$f$.

1. Знайти$f(-4), f(-2)$, і$f(0)$.

Малюнок$\PageIndex{59}$

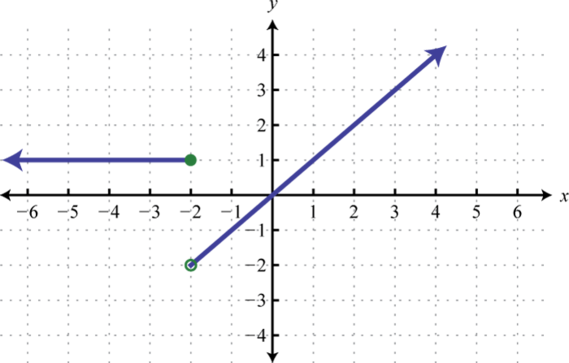
2. Знайти$f(−3), f(0)$, і$f(1)$.

Малюнок$\PageIndex{60}$

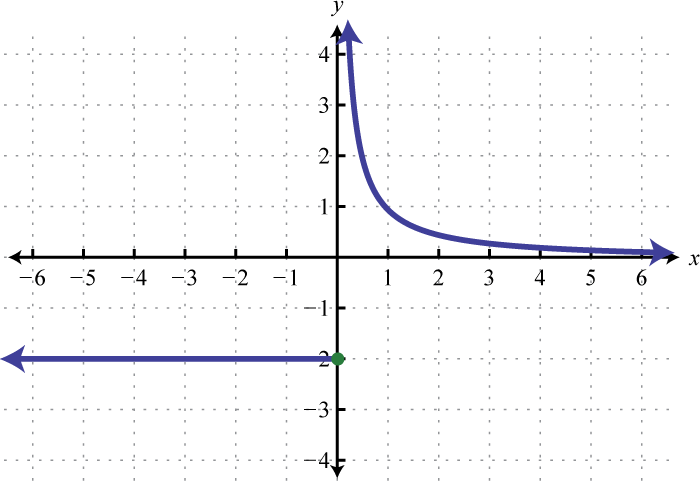
3. Знайти$f(0), f(2)$, і$f(4)$.

Малюнок$\PageIndex{61}$

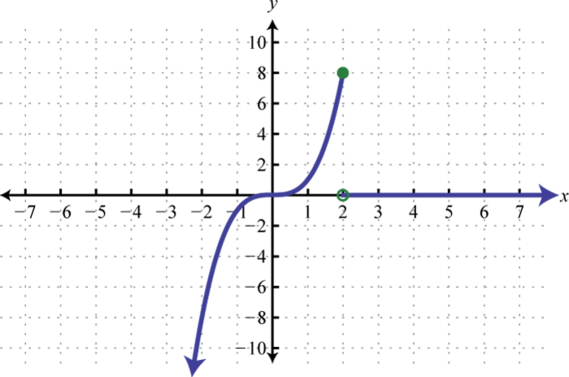
4. Знайти$f(−5), f(−2)$, і$f(2)$.

Малюнок$\PageIndex{62}$

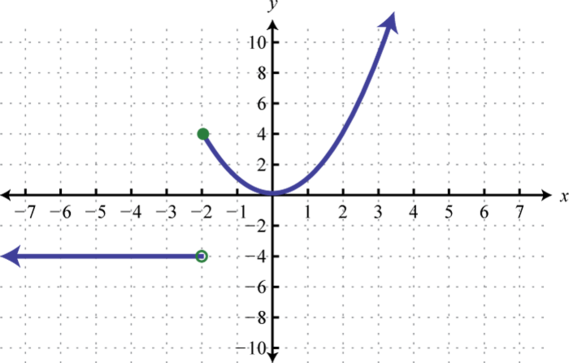
5. Знайти$f(−3), f(−2)$, і$f(2)$.

Малюнок$\PageIndex{63}$

6. Знайти$f(−3), f(0)$, і$f(4)$.

Малюнок$\PageIndex{64}$

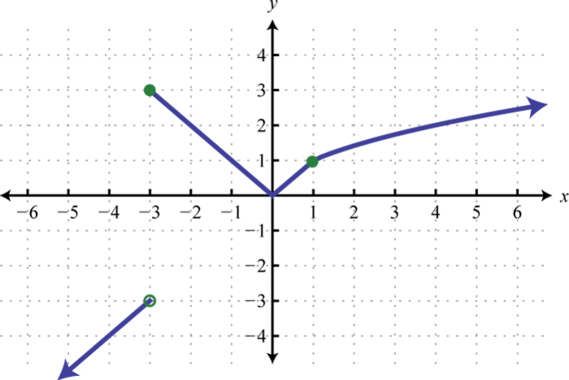
7. Знайти$f(−2), f(0)$, і$f(2)$.

Малюнок$\PageIndex{65}$

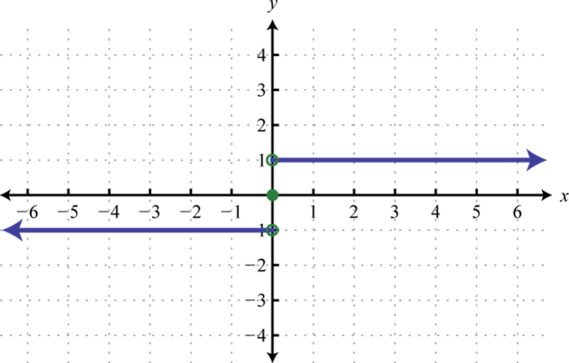
8. Знайти$f(−3), f(1)$, і$f(2)$.

Малюнок$\PageIndex{66}$

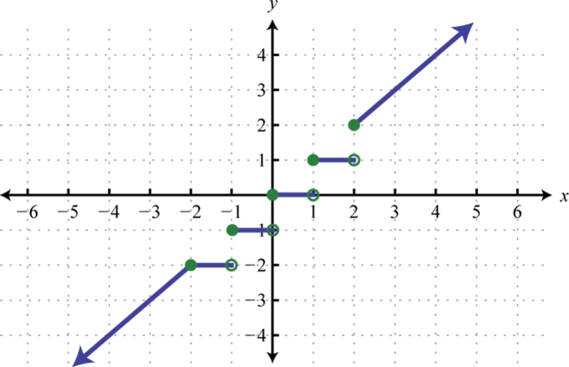
9. Вартість автомобіля в доларах дається в перерахунку на кількість років з моменту придбання нового в$1975$:

Малюнок$\PageIndex{67}$

(1) Визначте вартість автомобіля в році$1980$.

(2) В якому році оцінюється автомобіль$$9,000$?

10. Вартість одиниці в доларах нестандартних ламп залежить від кількості вироблених одиниць за наступним графіком:

Малюнок$\PageIndex{68}$

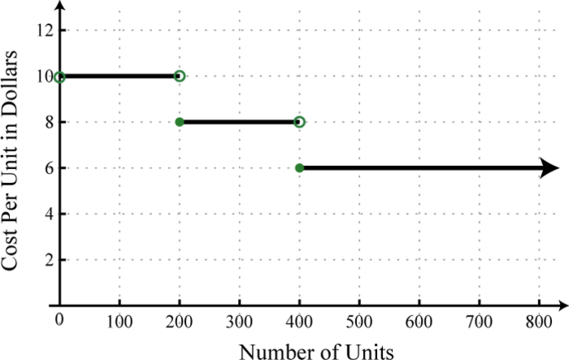
(1) Яка вартість одиниці, якщо виготовляються$250$ спеціальні лампи?

(2) Який рівень виробництва мінімізує вартість одиниці?

11. Продавець автомобілів заробляє комісію на основі загального обсягу продажів щомісяця$x$ відповідно до функції:

$( x ) = \left\{ \begin{array} { l l } { 0.03 x\quad \text { if } \quad 0 \leq x < \$ 20,000 } \\ { 0.05 x \quad\text { if } } \quad { \$ 20,000 \leq x < \$ 50,000 } \\ { 0.07 x \quad\text { if } }\quad { x \geq \$ 50,000 } \end{array} \right.$

(1) Якщо загальний обсяг продажів продавця за місяць є$$35,500$, яка її комісія відповідно до функції?

(2) Щоб вийти на наступний рівень у структурі комісії, скільки більше продажів їй знадобиться?

12. Прокат$$32$ човна коштує одну годину, а кожна додаткова година або часткова година коштує$$8$. Графік вартості прокату човна і визначте вартість оренди човна на$4 \frac{1}{2}$ години.

Відповідь

1. $f(−4) = 1, f(−2) = 1$, і$f(0) = 0$

3. $f(0) = 0, f(2) = 8$, і$f(4) = 0$

5. $f(−3) = 5, f(−2) = 4$, і$f(2) = 2$

7. $f(−2) = −1, f(0) = 0$, і$f(2) = 1$

9. (1)$$3,000$; (2)$2005$

11. (1)$$1,775$; (2)$$14,500$

Вправа$\PageIndex{9}$

1. Поясніть починаючому студенту алгебри, що таке асимптота.
2. Дослідіть і обговоріть різницю між функціями підлоги та стелі. Які програми ви можете знайти, які використовують ці функції?

Відповідь

1. Відповідь може відрізнятися

Виноски

⁴³ Будь-яка функція виду,$f(x) = c$ де$c$ є дійсним числом.

⁴⁴ Лінійна функція, визначена$f(x) = x$.

⁴⁵ Квадратична функція, визначена$f(x) = x^{2}$.

⁴⁶ Вигнутий графік, утворений функцією квадратизації.

⁴⁷ Кубічна функція, визначена$f(x) = x^{3}$.

⁴⁸ Функція, визначена за допомогою$f(x) = |x|$.

⁴⁹ Функція, визначена командою$f(x) = \sqrt{x}$.

⁵⁰ Функція, визначена за допомогою$f(x) = \frac{1}{x}$.

⁵¹ Вертикальна лінія, до якої граф стає нескінченно близьким.

⁵² Горизонтальна лінія, до якої графік стає нескінченно близьким, де$x$ -значення прагнуть до$±∞$.

⁵³ Функція, визначення якої змінюється залежно від значень у домені.

⁵⁴ Термін, який використовується при зверненні до кускової функції.

⁵⁵ Функція, яка присвоює будь-яке дійсне число$x$ найбільшому цілому числу, меншому або рівному$x$ позначеному$f(x) = \left[\!\![x]\!\!\right]$.

⁵⁶ Термін, який використовується при зверненні до найбільшої цілої функції.