Skip to main content
LibreTexts - Ukrayinska

9.7: Вищі коріння

  1. Last updated
  2. Save as PDF
  • Page ID
    58716

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    До кінця цього розділу ви зможете:

    • Спростіть вирази з вищими коренями
    • Використовуйте Product Property, щоб спростити вирази з вищими коренями
    • Скористайтеся властивістю Quotient, щоб спростити вирази з вищими коренями
    • Додайте і відніміть вищі коріння
    Примітка
    1. Спростити:\(y^{5}y^{4}\).
      Якщо ви пропустили цю проблему, перегляньте приклад 6.2.7.
    2. Спростити:\((n^2)^6\).
      Якщо ви пропустили цю проблему, перегляньте приклад 6.2.19.
    3. Спростити:\(\frac{x^8}{x^3}\).
      Якщо ви пропустили цю проблему, перегляньте приклад 6.5.1.

    Спрощення виразів за допомогою вищих коренів

    До теперішнього часу в цьому розділі ми працювали з квадратами та квадратними корінням. Зараз ми будемо розширювати нашу роботу, включивши вищі сили та вищі коріння.

    Давайте спочатку розглянемо деякі словникові запаси.

    \[\begin{array}{cc} {}&{}\\ {\textbf{We write:}}&{\textbf{We say:}}\\ {n^2}&{\text{n squared}}\\ {n^3}&{\text{n cubed}}\\ {n^4}&{\text{n to the fourth}}\\ {n^5}&{\text{n to the fifth}}\\ \nonumber \end{array}\]

    Терміни «квадрат» та «куб» походять від формул для площі квадрата та об'єму куба.

    Буде корисно мати таблицю ступенів цілих чисел від −5 до 5. Див\(\PageIdnex{1}\). Малюнок.

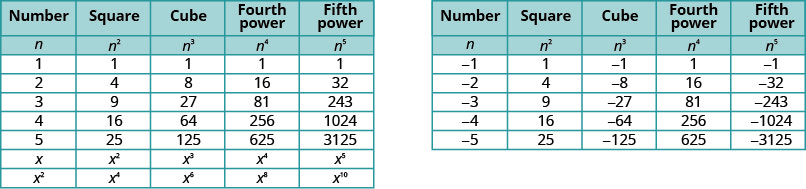
    Ця цифра складається з двох таблиць. Перша таблиця показує результати підняття чисел 1, 2, 3, 4, 5, х і х в квадраті до другої, третьої, четвертої і п'ятої степеней. У другій таблиці наведені результати підняття чисел негативного одного через негативну п'ять до другої, третьої, четвертої і п'ятої степеней. Перша таблиця має п'ять стовпців і дев'ять рядків. Другий має п'ять стовпців і сім рядків. Стовпці в обох таблицях позначені: «Число», «Квадрат», «Куб», «Четверта сила», «П'ята сила», «Ніщо», «Число», «Квадрат», «Куб», «Четверта сила» та «П'ята сила». В обох таблицях наступний рядок читає: n, n в квадраті, n в кубі, n до четвертого степеня, n до п'ятого ступеня, нічого, n, n в квадраті, n в кубі, n до четвертого степеня, і n до п'ятого степеня. У першій таблиці 1 в квадраті, 1 в кубі, 1 до четвертої потужності і 1 до п'ятої потужності показані як 1. У наступному ряду 2 в квадраті дорівнює 4, 2 куб дорівнює 8, 2 до четвертої потужності дорівнює 16, а 2 до п'ятої потужності 32. У наступному ряду 3 в квадраті дорівнює 9, 3 куб дорівнює 27, 3 до четвертого ступеня дорівнює 81, а 3 до п'ятої потужності 243. У наступному ряду 4 квадрата дорівнює 16, 4 куб дорівнює 64, 4 до четвертої потужності 246, а 4 до п'ятої потужності - 1024. У наступному ряду 5 в квадраті дорівнює 25, 5 куб дорівнює 125, 5 до четвертого ступеня дорівнює 625, а 5 до п'ятої потужності - 3125. У наступному ряду перераховані х в квадраті, х в кубі, х до четвертої степені, і х до п'ятої степені. У наступному рядку х у квадраті є х до четвертої степені, х в кубі квадрат є х до п'ятої степені, х в квадраті до четвертої потужності х до восьмої потужності, а х в квадраті до п'ятої потужності х до десятої степені. У другій таблиці негативний 1 в квадраті дорівнює 1, негативний 1 в кубі - негативний 1, негативний 1 до четвертої степені дорівнює 1, а негативний 1 до п'ятої - негативний 1. У наступному ряду негативний 2 в квадраті дорівнює 4, негативний 2 в кубі - негативний 8, негативний 2 до четвертої степені дорівнює 16, а негативний 2 до п'ятої - негативний 32. У наступному ряду негативний 4 в квадраті дорівнює 16, негативний 4 в кубі - негативний 64, негативний 4 до четвертої степені дорівнює 256, а негативний 4 до п'ятої - негативний 1024. У наступному ряду негативний 5 в квадраті дорівнює 25, негативний 5 в кубі - негативний 125, негативний 5 до четвертої степені дорівнює 625, а негативний 5 до п'ятої степені - негативний 3125.
    Рисунок\(\PageIndex{1}\): Від першого до п'ятого степенів цілих чисел від −5 до 5.

    Зверніть увагу на знаки на малюнку\(\PageIndex{1}\). Всі сили позитивних чисел, звичайно, позитивні. Але коли ми маємо негативне число, парні сили позитивні, а непарні - негативні. Ми скопіюємо рядок з повноваженнями −2 нижче, щоб допомогти вам побачити це.

    Ця цифра має п'ять стовпців і два рядки. Перший рядок позначає кожен стовпець: n, n у квадраті, n в кубі, n до четвертого степеня і n до п'ятого степеня. Другий ряд читає: негативні 2, 4, негативні 8, 16 і негативні 32.

    Раніше в цьому розділі ми визначили квадратний корінь числа.

    Якщо\(n^2=m\), то n - квадратний корінь m.

    І ми використовували позначення для\(\sqrt{m}\) позначення основного квадратного кореня. Так\(\sqrt{m} \ge 0\) завжди.

    Тепер ми поширимо визначення на вищі коріння.

    Визначення: N КОРІНЬ ЧИСЛА

    Якщо\(b^n=a\), то b - це і в корені числа a.

    Запис принципала в корені a\(\sqrt[n]{a}=b\)

    n називається індексом радикала.

    Індекс для квадратного кореня ми не пишемо. Так само, як ми використовуємо слово «куб» для\(b^3\), ми використовуємо термін «куб корінь» для\(\sqrt[3]{a}\).

    Ми посилаємося на Малюнок\(\PageIndex{1}\), щоб допомогти нам знайти вищі коріння.

    \[\begin{array}{cc} {4^3=64}&{\sqrt[3]{64}=4}\\ {3^4=81}&{\sqrt[4]{81}=3}\\ {(−2)^5=−32}&{\sqrt[5]{−32}=−2}\\ \nonumber \end{array}\]

    Чи можемо ми мати парний корінь негативного числа? Ні. Ми знаємо, що квадратний корінь від'ємного числа не є дійсним числом. Те ж саме справедливо і для будь-якого рівного кореня. Парні корені від'ємних чисел не є дійсними числами. Непарні корені від'ємних чисел є дійсними числами.

    Визначення: ВЛАСТИВОСТІ\(\sqrt[n]{a}\)

    Коли n - парне число і

    • \(a\ge 0\), то\(\sqrt[n]{a}\) є дійсним числом
    • \(a < 0\), то не\(\sqrt[n]{a}\) є дійсним числом

    Коли n - непарне число,\(\sqrt[n]{a}\) є дійсним числом для всіх значень a.

    Приклад\(\PageIndex{1}\)

    Спростити:

    1. \(\sqrt[3]{8}\)
    2. \(\sqrt[4]{81}\)
    3. \(\sqrt[5]{32}\).
    Відповідь
    1. \(\sqrt[3]{8}\)
    З тих пір\((2)^3=8\). 2
    2. \(\sqrt[4]{81}\)
    З тих пір\((3)^4=81\). 3
    3. \(\sqrt[5]{32}\)
    З тих пір\((2)^5=32\). 2
    Приклад\(\PageIndex{2}\)

    Спростити:

    1. \(\sqrt[3]{27}\)
    2. \(\sqrt[4]{256}\)
    3. \(\sqrt[5]{243}\).
    Відповідь
    1. 3
    2. 4
    3. 3
    Приклад\(\PageIndex{3}\)

    Спростити:

    1. \(\sqrt[3]{1000}\)
    2. \(\sqrt[4]{16}\)
    3. \(\sqrt[5]{32}\).
    Відповідь
    1. 10
    2. 2
    3. 2
    Приклад\(\PageIndex{4}\)

    Спростити:

    1. \(\sqrt[3]{−64}\)
    2. \(\sqrt[4]{−16}\)
    3. \(\sqrt[5]{−243}\).
    Відповідь
    1. \(\sqrt[3]{−64}\)
    З тих пір\((−4)^3=−64\). −4
    2. \(\sqrt[4]{−16}\)
    Подумайте,\((?)^4=−16\) .Ніяке реальне число, підняте до четвертої влади, не є позитивним. Чи не дійсне число.
    3. \(\sqrt[5]{−243}\)
    З тих пір\((−3)^5=−243\). −3
    Приклад\(\PageIndex{5}\)

    Спростити:

    1. \(\sqrt[3]{−125}\)
    2. \(\sqrt[4]{−16}\)
    3. \(\sqrt[5]{−32}\).
    Відповідь
    1. −5
    2. не реальний
    3. −2
    Приклад\(\PageIndex{6}\)

    Спростити:

    1. \(\sqrt[3]{−216}\)
    2. \(\sqrt[4]{−81}\)
    3. \(\sqrt[5]{−1024}\).
    Відповідь
    1. −6
    2. не реальний
    3. −4
    Коли ми працювали з квадратними коренями, які мали змінні в радиканді, ми обмежили змінні до невід'ємних значень. Зараз ми знімемо це обмеження.

    Непарний корінь числа може бути як позитивним, так і негативним. Ми це бачили\(\sqrt[3]{−64}=−4\).

    Але парний корінь невід'ємного числа завжди невід'ємний, тому що ми беремо принципал n -й корінь.

    Припустимо, ми починаємо з a=−5.

    \[\begin{array}{cc} {(−5)^4=625}&{\sqrt[4]{625}=5}\\ \nonumber \end{array}\]

    Як ми можемо переконатися, що четвертий корінь −5, піднятий до четвертої степені,\((−5)^4\) дорівнює 5? Ми побачимо в наступному властивості.

    Визначення: СПРОЩЕННЯ НЕПАРНИХ І ПАРНИХ КОРЕНІВ

    Для будь-якого цілого числа\(n \ge 2\),

    \[\begin{array}{cc} {\text{when n is odd}}&{\sqrt[n]{a^n}=a}\\ {\text{when n is even}}&{\sqrt[n]{a^n}=|a|}\\ \nonumber \end{array}\]

    Ми повинні використовувати знаки абсолютного значення, коли беремо парний корінь виразу зі змінною в радикалі.

    Приклад\(\PageIndex{7}\)

    Спростити:

    1. \(\sqrt{x^2}\)
    2. \(\sqrt[3]{n^3}\)
    3. \(\sqrt[4]{p^4}\)
    4. \(\sqrt[5]{y^5}\).
    Відповідь

    Ми використовуємо абсолютне значення, щоб обов'язково отримати позитивний корінь.

    1. \(\sqrt{x^2}\)
    Так як\((x)^2=x^2\) і ми хочемо позитивного кореня. |x|
    2. \(\sqrt[3]{n^3}\)
    З тих пір\((n)^3=n^3\). Це непарний корінь, тому немає необхідності в знаку абсолютного значення. п
    3. \(\sqrt[4]{p^4}\)
    Так як\((p)^4=p^4\) і ми хочемо позитивного кореня. |п|
    4. \(\sqrt[5]{y^5}\)
    З тих пір\((y)^5=y^5\). Це непарний корінь, тому немає необхідності в знаку абсолютного значення. у
    Приклад\(\PageIndex{8}\)

    Спростити:

    1. \(\sqrt{b^2}\)
    2. \(\sqrt[3]{w^3}\)
    3. \(\sqrt[4]{m^4}\)
    4. \(\sqrt[5]{q^5}\).
    Відповідь
    1. |б|
    2. ш
    3. |м|
    4. q
    Приклад\(\PageIndex{9}\)

    Спростити:

    1. \(\sqrt{y^2}\)
    2. \(\sqrt[3]{p^3}\)
    3. \(\sqrt[4]{z^4}\)
    4. \(\sqrt[5]{q^5}\)
    Відповідь
    1. |y|
    2. р
    3. |з|
    4. q
    Приклад\(\PageIndex{10}\)

    Спростити:

    1. \(\sqrt[3]{y^{18}}\)
    2. \(\sqrt[4]{z^8}\).
    Відповідь
    1. \(\sqrt[3]{y^{18}}\)
    З тих пір\((y^6)^3=y^18\). \(\sqrt[3]{(y^6)^3}\)
      \(y^6\)
    2. \(\sqrt[4]{z^8}\)
    З тих пір\((z^2)^4=z^8\). \(\sqrt[4]{(z^2)^4}\)
    Оскільки\(z^2\) позитивний, нам не потрібен знак абсолютного значення. \(z^2\)
    Приклад\(\PageIndex{11}\)

    Спростити:

    1. \(\sqrt[4]{u^{12}}\)
    2. \(\sqrt[3]{v^{15}}\).
    Відповідь
    1. \(u^3\)
    2. \(v^5\)
    Приклад\(\PageIndex{12}\)

    Спростити:

    1. \(\sqrt[5]{c^{20}}\)
    2. \(\sqrt[6]{d^{24}}\).
    Відповідь
    1. \(c^4\)
    2. \(d^4\)
    Приклад\(\PageIndex{13}\)

    Спростити:

    1. \(\sqrt[3]{64p^6}\)
    2. \(\sqrt[4]{16q^{12}}\).
    Відповідь
    1. \(\sqrt[3]{64p^6}\)
    Перепишіть\(64p^6\) як\((4p^2)^3\). \(\sqrt[3]{(4p^2)^3}\)
    Візьміть кубик кореня. \(4p^2\)
    2. \(\sqrt[4]{16q^{12}}\)
    Перепишіть радиканд як четверту потужність. \(\sqrt[4]{(2q^3)^4}\)
    Візьміть четвертий корінь. \(2|q^3|\)
    Приклад\(\PageIndex{14}\)

    Спростити:

    1. \(\sqrt[3]{27x^{27}}\)
    2. \(\sqrt[4]{81q^{28}}\).
    Відповідь
    1. \(3x^9\)
    2. \(3∣q^7∣\)
    Приклад\(\PageIndex{15}\)

    Спростити:

    1. \(\sqrt[3]{125p^9}\)
    2. \(\sqrt[5]{243q^{25}}\)
    Відповідь
    1. \(5p^3\)
    2. \(3q^5\)

    Використовуйте властивість Product для спрощення виразів з вищими коренями

    Ми спростимо вирази з вищими коренями майже так само, як ми спростили вирази з квадратними коренями. А в корені вважається спрощеним, якщо він не має факторів\(m^n\).

    Визначення: СПРОЩЕНО В КОРЕНІ

    \(\sqrt[n]{a}\)вважається спрощеним, якщо не має факторів\(m^n\).

    Ми узагальнимо властивість продукту квадратних коренів, щоб включити будь-який цілочисельний корінь.\(n \ge 2\).

    Визначення: ВЛАСТИВІСТЬ ПРОДУКТУ N TH КОРЕНІВ

    \(\sqrt[n]{ab}=\sqrt[n]{a}·\sqrt[n]{b}\)і\(\sqrt[n]{a}·\sqrt[n]{b}=\sqrt[n]{ab}\)

    коли\(\sqrt[n]{a}\) і\(\sqrt[n]{b}\) є дійсними числами і для будь-якого цілого числа\(n \ge 2\)

    Приклад\(\PageIndex{16}\)

    Спростити:

    1. \(\sqrt[3]{x^4}\)
    2. \(\sqrt[4]{x^7}\).
    Відповідь

    1.

    		 \(\sqrt[3]{x^4}\)
    Перепишіть радиканд як продукт, використовуючи найбільший коефіцієнт ідеального куба. \(\sqrt[3]{x^3·x}\)
    Перепишіть радикал як добуток двох радикалів. \(\sqrt[3]{x^3}·\sqrt[3]{x}\)
    Спростити. \(x\sqrt[3]{x}\)
    2. \(\sqrt[4]{x^7}\)
    Перепишіть радиканд як продукт, використовуючи найбільший ідеальний четвертий коефіцієнт потужності. \(\sqrt[4]{x^4·x^3}\)
    Перепишіть радикал як добуток двох радикалів. \(\sqrt[4]{x^4}·\sqrt[4]{x^3}\)
    Спростити. \(|x|\sqrt[4]{x^3}\)
    Приклад\(\PageIndex{17}\)

    Спростити:

    1. \(\sqrt[4]{y^6}\)
    2. \(\sqrt[3]{z^5}\).
    Відповідь
    1. \(|y∣\sqrt[4]{y^2}\)
    2. \(z\sqrt[3]{z^2}\)
    Приклад\(\PageIndex{18}\)

    Спростити:

    1. \(\sqrt[5]{p^8}\)
    2. \(\sqrt[6]{q^{13}}\).
    Відповідь
    1. \(p\sqrt[5]{p^3}\)
    2. \( q^2\sqrt[6]{q}\)
    Приклад\(\PageIndex{19}\)

    Спростити:

    1. \(\sqrt[3]{16}\)
    2. \(\sqrt[4]{243}\).
    Відповідь
    1. \(\sqrt[3]{16}\)
      \(\sqrt[3]{2^4}\)
    Перепишіть радиканд як продукт, використовуючи найбільший коефіцієнт ідеального куба. \(\sqrt[3]{2^3·2}\)
    Перепишіть радикал як добуток двох радикалів. \(\sqrt[3]{2^3}·\sqrt[3]{2}\)
    Спростити. \(2\sqrt[3]{2}\)
    2. \(\sqrt[4]{243}\)
      \(\sqrt[4]{3^5}\)
    Перепишіть радиканд як продукт, використовуючи найбільший ідеальний четвертий коефіцієнт потужності. \(\sqrt[4]{3^4·3}\)
    Перепишіть радикал як добуток двох радикалів. \(\sqrt[4]{3^4}·\sqrt[4]{3}\)
    Спростити. \(3\sqrt[4]{3}\)
    Приклад\(\PageIndex{20}\)

    Спростити:

    1. \(\sqrt[3]{81}\)
    2. \(\sqrt[4]{64}\).
    Відповідь
    1. \(3\sqrt[3]{3}\)
    2. \(2\sqrt[4]{4}\)
    Приклад\(\PageIndex{21}\)

    Спростити:

    1. \(\sqrt[3]{625}\)
    2. \(\sqrt[4]{729}\).
    Відповідь
    1. \(5\sqrt[3]{5}\)
    2. \(3\sqrt[4]{9}\)

    Не забувайте використовувати знаки абсолютного значення, коли берете парний корінь виразу зі змінною в радикалі.

    Приклад\(\PageIndex{22}\)

    Спростити:

    1. \(\sqrt[3]{24x^7}\)
    2. \(\sqrt[4]{80y^{14}}\).
    Відповідь
    1. \(\sqrt[3]{24x^7}\)
    Перепишіть радиканд як продукт, використовуючи ідеальні кубові фактори. \(\sqrt[3]{2^{3}x^{6}·3x}\)
    Перепишіть радикал як добуток двох радикалів. \(\sqrt[3]{2^{3}x^{6}}·\sqrt[3]{3x}\)
    Перепишіть перший радиканд як\((2x^2)^3\) \(\sqrt[3]{(2x^{2})^3}·\sqrt[3]{3x}\)
    Спростити. \(2x^2\sqrt[3]{3x}\)
    2. \(\sqrt[4]{80y^{14}}\)
    Перепишіть радиканд як продукт, використовуючи ідеальні четверті коефіцієнти потужності. \(\sqrt[4]{2^{4}y^{12}·5y^2}\)
    Перепишіть радикал як добуток двох радикалів. \(\sqrt[4]{2^{4}y^{12}}·\sqrt[4]{5y^2}\)
    Перепишіть перший радиканд як\((2y^3)^4\) \(\sqrt[4]{(2y^3)^4}·\sqrt[4]{5y^2}\)
    Спростити. \(2|y^3|\sqrt[4]{5y^2}\)
    Приклад\(\PageIndex{23}\)

    Спростити:

    1. \(\sqrt[3]{54p^[10}]\)
    2. \(\sqrt[4]{64q^{10}}\).
    Відповідь
    1. \(3p^3\sqrt[3]{2p}\)
    2. \(2q^2\sqrt[4]{4q^2}\)
    Приклад\(\PageIndex{24}\)

    Спростити:

    1. \(\sqrt[3]{128m^{11}}\)
    2. \(\sqrt[4]{162n^7}\).
    Відповідь
    1. \(4m^3\sqrt[3]{2m^2}\)
    2. \(3|n|\sqrt[4]{2n^3}\)
    Приклад\(\PageIndex{25}\)

    Спростити:

    1. \(\sqrt[3]{−27}\)
    2. \(\sqrt[4]{−16}\).
    Відповідь
    1. \(\sqrt[3]{−27}\)
    Перепишіть радиканд як продукт, використовуючи ідеальні кубові фактори. \(\sqrt[3]{(−3)^3}\)
    Візьміть кубик кореня. −3
    2. \(\sqrt[4]{−16}\)
    Там немає дійсного числа n де\(n^4=−16\). Чи не дійсне число.
    Приклад\(\PageIndex{26}\)

    Спростити:

    1. \(\sqrt[3]{−108}\)
    2. \(\sqrt[4]{−48}\).
    Відповідь
    1. \(−3\sqrt[3]{4}\)
    2. не реальний
    Приклад\(\PageIndex{27}\)

    Спростити:

    1. \(\sqrt[3]{−625}\)
    2. \(\sqrt[4]{−324}\).
    Відповідь
    1. \(−5\sqrt[3]{5}\)
    2. не реальний

    Використовуйте властивість коефіцієнта для спрощення виразів з вищими коренями

    Ми можемо спростити вищі коріння за допомогою коефіцієнтів так само, як ми спростили квадратні коріння. Спочатку спрощуємо будь-які дроби всередині радикала.

    Приклад\(\PageIndex{28}\)

    Спростити:

    1. \(\sqrt[3]{\frac{a^8}{a^5}}\)
    2. \(\sqrt[4]{\frac{a^{10}}{a^2}}\).
    Відповідь

    1.

    		 \(\sqrt[3]{\frac{a^8}{a^5}}\)
    Спростити дріб під радикалом першим. \(\sqrt[3]{a^3}\)
    Спростити. a
    2. \(\sqrt[4]{\frac{a^{10}}{a^2}}\)
    Спростити дріб під радикалом першим. \(\sqrt[4]{a^8}\)
    Перепишіть радиканд, використовуючи ідеальні четверті коефіцієнти потужності. \(\sqrt[4]{(a^2)^4}\)
    Спростити. \(a^2\)
    Приклад\(\PageIndex{29}\)

    Спростити:

    1. \(\sqrt[4]{\frac{x^7}{x^3}}\)
    2. \(\sqrt[4]{\frac{y^{17}}{y^5}}\).
    Відповідь
    1. |x|
    2. \(y^3\)
    Приклад\(\PageIndex{30}\)

    Спростити:

    1. \(\sqrt[3]{\frac{m^{13}}{m^7}}\)
    2. \(\sqrt[5]{\frac{n^{12}}{n^2}}\).
    Відповідь
    1. \(m^2\)
    2. \(n^2\)

    Раніше ми використовували властивість «в зворотному напрямку» для спрощення квадратних коренів. Тепер узагальнимо формулу, щоб включити вищі коріння.

    Визначення: ЧАСТКОВА ВЛАСТИВІСТЬ N КОРЕНІВ

    \(\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\)і\(\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}\)

    коли\(\sqrt[n]{a}\) and \(\sqrt[n]{b}\) are real numbers, \(b \ne 0\), and for any integer \(n \ge 2\)

    Вправа\(\PageIndex{31}\)

    Спростити:

    1. \(\frac{\sqrt[3]{−108}}{\sqrt[3]{2}}\)
    2. \(\frac{\sqrt[4]{96x^7}}{\sqrt[4]{3x^2}}\)
    Відповідь
    1. \(\frac{\sqrt[3]{−108}}{\sqrt[3]{2}}\)
    Жоден радиканд не є ідеальним кубом, тому використовуйте властивість Quotient, щоб написати як один радикал. \(\sqrt[3]{\frac{−108}{2}}\)
    Спростити дріб під радикалом. \(\sqrt[3]{−54}\)
    Перепишіть радиканд як продукт, використовуючи ідеальні кубові фактори. \(\sqrt[3]{(−3)^3·2}\)
    Перепишіть радикал як добуток двох радикалів. \(\sqrt[3]{(−3)^3}·\sqrt[3]{2}\)
    Спростити. \(−3\sqrt[3]{2}\)
    2. \(\frac{\sqrt[4]{96x^7}}{\sqrt[4]{3x^2}}\)
    Жоден радиканд не є ідеальною четвертою силою, тому використовуйте властивість частки писати як один радикал \(\sqrt[4]{\frac{96x^7}{3x^2}}\)
    Спростити дріб під радикалом. \(\sqrt[4]{32x^5}\)
    Перепишіть радиканд як продукт, використовуючи ідеальні четверті коефіцієнти потужності. \(\sqrt[4]{2^{4}x^4·2x}\)
    Перепишіть радикал як добуток двох радикалів. \(\sqrt[4]{(2x)^4}·\sqrt[4]{2x}\)
    Спростити. \(2|x|\sqrt[4]{2x}\)
    Приклад\(\PageIndex{32}\)

    Спростити:

    1. \(\frac{\sqrt[3]{−532}}{\sqrt[3]{2}}\)
    2. \(\frac{\sqrt[4]{486m^{11}}}{\sqrt[4]{3m^5}}\)
    Відповідь
    1. не реальний
    2. \(3|m|\sqrt[4]{2m^2}\)
    Приклад\(\PageIndex{33}\)

    Спростити:

    1. \(\frac{\sqrt[3]{−192}}{\sqrt[3]{3}}\)
    2. \(\frac{\sqrt[4]{324n^7}}{\sqrt[4]{2n^3}}\).
    Відповідь
    1. −4
    2. \(3|n|\sqrt[4]{2}\)

    Якщо дріб всередині радикала не може бути спрощений, ми використовуємо першу форму властивості частки, щоб переписати вираз як частку двох радикалів.

    Приклад\(\PageIndex{34}\)

    Спростити:

    1. \(\sqrt[3]{\frac{24x^7}{y^3}}\)
    2. \(\sqrt[4]{\frac{48x^{10}}{y^8}}\).
    Відповідь
    1. \(\sqrt[3]{\frac{24x^7}{y^3}}\)
    Дріб в радиканді спростити неможливо. Використовуйте властивість частки, щоб написати як два радикали. \(\frac{\sqrt[3]{24x^7}}{\sqrt[3]{y^3}}\)
    Перепишіть кожен радиканд як продукт, використовуючи ідеальні кубові фактори. \(\frac{\sqrt[3]{8x^6·3x}}{\sqrt[3]{y^3}}\)
    Перепишіть чисельник як добуток двох радикалів. \(\frac{\sqrt[3]{(2x^2)^3}·\sqrt[3]{3x}}{\sqrt[3]{y^3}}\)
    Спростити. \(\frac{2x^2\sqrt[3]{3x}}{y}\)
    2. \(\sqrt[4]{\frac{48x^{10}}{y^8}}\)
    Дріб в радиканді спростити неможливо. Використовуйте властивість частки, щоб написати як два радикали. \(\frac{\sqrt[4]{48x^{10}}}{\sqrt[4]{y^8}}\)
    Перепишіть кожен радиканд як продукт, використовуючи ідеальні кубові фактори. \(\frac{\sqrt[4]{16x^8·3x^2}}{\sqrt[4]{y^8}}\)
    Перепишіть чисельник як добуток двох радикалів. \(\frac{\sqrt[4]{(2x^2)^4}·\sqrt[4]{3x^2}}{\sqrt[4]{(y^2)^4}}\)
    Спростити. \(\frac{2x^2\sqrt[4]{3x^2}}{y^2}\)
    Приклад\(\PageIndex{35}\)

    Спростити:

    1. \(\sqrt[3]{\frac{108c^{10}}{d^6}}\)
    2. \(\sqrt[4]{\frac{80x^{10}}{y^5}}\).
    Відповідь
    1. \(\frac{3c^3\sqrt[3]{4c}}{d^2}\)
    2. \(\frac{x^2}{∣y∣}\sqrt[4]{\frac{80x^2}{y}}\)
    Приклад\(\PageIndex{36}\)

    Спростити:

    1. \(\sqrt[3]{\frac{40r^3}{s}}\)
    2. \(\sqrt[4]{\frac{162m^{14}}{n^{12}}}\)
    Відповідь
    1. \(r\sqrt[3]{\frac{40}{s}}\)
    2. \(\frac{3m^3\sqrt[4]{2m^2}}{∣n^3∣}\)

    Додавання та віднімання вищих коренів

    Ми можемо додавати та віднімати вищі коріння, як ми додали та віднімали квадратні коріння. Спочатку ми надаємо формальне визначення подібних радикалів.

    Визначення: ЯК РАДИКАЛИ

    Радикали з однаковим показником і однаковим радикалом називаються подібними радикалами.

    Подібні радикали мають однаковий індекс і той же радиканд.

    • \(9\sqrt[4]{42x}\)і\(−2\sqrt[4]{42x}\) схожі на радикалів.
    • \(5\sqrt[3]{125x}\)і не\(6\sqrt[3]{125y}\) схожі на радикалів. Радиканди бувають різними.
    • \(2\sqrt[5]{1000q}\)і не\(−4\sqrt[4]{1000q}\) схожі на радикалів. Індекси різні.

    Ми додаємо і віднімаємо як радикали так само, як ми додаємо і віднімаємо як терміни. Ми можемо додати\(9\sqrt[4]{42x}+(−2\sqrt[4]{42x})\) і результат є\(7\sqrt[4]{42x}\).

    Приклад\(\PageIndex{37}\)

    Спростити:

    1. \(\sqrt[3]{4x}+\sqrt[3]{4x}\)
    2. \(4\sqrt[4]{8}−2\sqrt[4]{8}\)
    Відповідь
    1. \(\sqrt[3]{4x}+\sqrt[3]{4x}\)
    Радикали схожі, тому ми додаємо коефіцієнти \(2\sqrt[3]{4x}\)
    2. \(4\sqrt[4]{8}−2\sqrt[4]{8}\)
    Радикали схожі, тому ми віднімаємо коефіцієнти. \(2\sqrt[4]{8}\)
    Приклад\(\PageIndex{38}\)

    Спростити:

    1. \(\sqrt[5]{3x}+\sqrt[5]{3x}\)
    2. \(3\sqrt[3]{9}−\sqrt[3]{9}\)
    Відповідь
    1. \(2\sqrt[5]{3x}\)
    2. \(2\sqrt[3]{9}\)
    Приклад\(\PageIndex{39}\)

    Спростити:

    1. \(\sqrt[4]{10y}+\sqrt[4]{10y}\)
    2. \(5\sqrt[6]{32}−3\sqrt[6]{32}\).
    Відповідь
    1. \(2\sqrt[4]{10y}\)
    2. \(2\sqrt[6]{32}\)

    Коли вираз, здається, не має подібних радикалів, ми спочатку спростимо кожен радикал. Іноді це призводить до виразу з подібними радикалами.

    Приклад\(\PageIndex{40}\)

    Спростити:

    1. \(\sqrt[3]{54}−\sqrt[3]{16}\)
    2. \(\sqrt[4]{48}+\sqrt[4]{243}\).
    Відповідь
    1. \(\sqrt[3]{54}−\sqrt[3]{16}\)
    Перепишіть кожен радиканд, використовуючи ідеальні кубові фактори. \(\sqrt[3]{27}·\sqrt[3]{2}−\sqrt[3]{8}·\sqrt[3]{2}\)
    Перепишіть ідеальні кубики. \(\sqrt[3]{(3)^3}·\sqrt[3]{2}−\sqrt[3]{(2)^3}·\sqrt[3]{2}\)
    Спрощуйте радикали там, де це можливо. \(3\sqrt[3]{2}−2\sqrt[3]{2}\)
    Поєднуються як радикали. \(\sqrt[3]{2}\)
    2. \(\sqrt[4]{48}+\sqrt[4]{243}\)
    Перепишіть, використовуючи ідеальні четверті коефіцієнти потужності. \(\sqrt[4]{16}·\sqrt[4]{3}+\sqrt[4]{81}·\sqrt[4]{3}\)
    Перепишіть кожен радиканд як продукт, використовуючи ідеальні кубові фактори. \(\sqrt[4]{(2)^4}·\sqrt[4]{3}+\sqrt[4]{(3)^4}·\sqrt[4]{3}\)
    Перепишіть чисельник як добуток двох радикалів. \(2\sqrt[4]{3}+3\sqrt[4]{3}\)
    Спростити. \(5\sqrt[4]{3}\)
    Приклад\(\PageIndex{41}\)

    Спростити:

    1. \(\sqrt[3]{192}−\sqrt[3]{81}\)
    2. \(\sqrt[4]{32}+\sqrt[4]{512}\).
    Відповідь
    1. \(\sqrt[3]{3}\)
    2. \(6\sqrt[4]{2}\)
    Приклад\(\PageIndex{42}\)

    Спростити:

    1. \(\sqrt[3]{108}−\sqrt[3]{250}\)
    2. \(\sqrt[5]{64}+\sqrt[5]{486}\).
    Відповідь
    1. \(−\sqrt[3]{2}\)
    2. \(5\sqrt[5]{2}\)
    Приклад\(\PageIndex{43}\)

    Спростити:

    1. \(\sqrt[3]{24x^4}−\sqrt[3]{−81x^7}\)
    2. \(\sqrt[4]{162y^9}+\sqrt[4]{512y^5}\).
    Відповідь
    1. \(\sqrt[3]{24x^4}−\sqrt[3]{−81x^7}\)
    Перепишіть кожен радиканд, використовуючи ідеальні кубові фактори. \(\sqrt[3]{8x^3}·\sqrt[3]{3x}−\sqrt[3]{−27x^6}·\sqrt[3]{3x}\)
    Перепишіть ідеальні кубики. \(\sqrt[3]{(2x)^3}·\sqrt[3]{3x}−\sqrt[3]{(−3x^2)^3}·\sqrt[3]{3x}\)
    Спрощуйте радикали там, де це можливо. \(2x\sqrt[3]{3x}−(−3x^2\sqrt[3]{3x})\)
    2. \(\sqrt[4]{162y^9}+\sqrt[4]{516y^5}\)
    Перепишіть, використовуючи ідеальні четверті коефіцієнти потужності. \(\sqrt[4]{81y^8}·\sqrt[4]{2y}+\sqrt[4]{256y^4}·\sqrt[4]{2y}\)
    Перепишіть кожен радиканд як продукт, використовуючи ідеальні кубові фактори. \(\sqrt[4]{(3y^2)^4}·\sqrt[4]{2y}+\sqrt[4]{(4y)^4}·\sqrt[4]{2y}\)
    Перепишіть чисельник як добуток двох радикалів. \(3y^2\sqrt[4]{2y}+4|y|\sqrt[4]{2y}\)
    Приклад\(\PageIndex{44}\)

    Спростити:

    1. \(\sqrt[3]{32y^5}−\sqrt[3]{−108y^8}\)
    2. \(\sqrt[4]{243r^{11}}+\sqrt[4]{768r^{10}}\).
    Відповідь
    1. \(2y\sqrt[3]{4y^2}+3y^2\sqrt[3]{4y^2}\)
    2. \(3r^2\sqrt[4]{3r^3}+4r^2\sqrt[4]{3r^2}\)
    Приклад\(\PageIndex{45}\)

    Спростити:

    1. \(\sqrt[3]{40z^7}−\sqrt[3]{−135z^4}\)
    2. \(\sqrt[4]{80s^{13}}+\sqrt[4]{1280s^6}\).
    Відповідь
    1. \(2z^2\sqrt[3]{5z}+3z^5\sqrt[3]{5z}\)
    2. \(2∣s^3∣\sqrt[4]{5s}+4|s|\sqrt[4]{5s}\)
    Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики зі спрощенням вищих коренів.
    • Спрощення вищих коренів
    • Додавання/віднімання коренів з вищими індексами

    Ключові концепції

    • властивості
    • \(\sqrt[n]{a}\)коли n - парне число і
      • \(a \ge 0\), то\(\sqrt[n]{a}\) є дійсним числом
      • \(a < 0\), то не\(\sqrt[n]{a}\) є дійсним числом
      • Коли n - непарне число,\(\sqrt[n]{a}\) є дійсним числом для всіх значень a.
      • Для будь-якого цілого числа\(n \ge 2\), коли n непарне\(\sqrt[n]{a^n}=a\)
      • Для будь-якого цілого числа\(n \ge 2\), коли n парне\(\sqrt[n]{a^n}=|a|\)
    • \(\sqrt[n]{a}\)вважається спрощеним, якщо не має факторів\(m^n\).
    • \(\sqrt[n]{ab}=\sqrt[n]{a}·\sqrt[n]{b}\)і\(\sqrt[n]{a}·\sqrt[n]{b}=\sqrt[n]{ab}\)
    • \(\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\)і\(\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}\)
    • Щоб об'єднати як радикали, просто додайте або відніміть коефіцієнти, зберігаючи радикал однаковим.

    Глосарій

    У корені числа
    Якщо\(b^n=a\), то b - і в корені a.
    принципова в корені
    Написано принципал в корені a\(\sqrt[n]{a}\).
    індекс
    \(\sqrt[n]{a}\)n називається індексом радикала.
    як радикали
    Радикали з однаковим показником і однаковим радикалом називаються подібними радикалами.