7.6: Квадратні рівняння
- Page ID
- 58747
До кінця цього розділу ви зможете:
- Розв'яжіть квадратні рівняння за допомогою властивості нульового добутку
- Вирішити квадратні рівняння факторингу
- Розв'язуйте програми, змодельовані квадратними рівняннями
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Вирішити:\(5y−3=0\).
Якщо ви пропустили цю проблему, перегляньте Вправа 2.3.1. - Вирішити:\(10a=0\).
Якщо ви пропустили цю проблему, перегляньте Вправа 2.2.1. - Поєднуйте подібні терміни:\(12 x^{2}-6 x+4 x\).
Якщо ви пропустили цю проблему, перегляньте Вправа 1.3.37. - Фактор\(n^{3}-9 n^{2}-22 n\) повністю.
Якщо ви пропустили цю проблему, перегляньте Вправа 7.3.10.
Ми вже розв'язали лінійні рівняння, рівняння виду\(a x+b y=c\). У лінійних рівняннях змінні не мають показників. Квадратні рівняння - це рівняння, в яких змінна зведена в квадрат. Нижче наведено кілька прикладів квадратичних рівнянь:
\[x^{2}+5 x+6=0 \quad 3 y^{2}+4 y=10 \quad 64 u^{2}-81=0 \quad n(n+1)=42\]
Останнє рівняння, здається, не має змінної в квадраті, але коли ми спростимо вираз зліва, ми отримаємо\(n^{2}+n\).
Загальна форма квадратного рівняння -\(a x^{2}+b x+c=0\), с\(a \neq 0\).
Рівняння виду\(a x^{2}+b x+c=0\) називається квадратним рівнянням.
\[a, b, \text { and } c \text { are real numbers and } a \neq 0\]
Для розв'язання квадратичних рівнянь потрібні методи, відмінні від тих, які ми використовували при розв'язанні лінійних рівнянь. Ми розглянемо один метод тут, а потім кілька інших в наступному розділі.
Розв'язування квадратичних рівнянь за допомогою властивості нульового добутку
Спочатку ми вирішимо деякі квадратні рівняння за допомогою властивості нульового продукту. Властивість нульового продукту говорить, що якщо добуток двох величин дорівнює нулю, то повинно бути, що хоча б одна з величин дорівнює нулю. Єдиний спосіб отримати добуток, рівний нулю - помножити на сам нуль.
\(\text { If } a \cdot b=0, \text { then either } a=0 \text { or } b=0 \text { or both. }\)
Тепер ми будемо використовувати властивість нульового продукту, щоб вирішити квадратне рівняння.
Вирішити:\((x+1)(x-4)=0\)
- Відповідь
-



Вирішити:\((x-3)(x+5)=0\)
- Відповідь
-
\(x=3, x=-5\)
Вирішити:\((y-6)(y+9)=0\)
- Відповідь
-
\(y=6, y=-9\)
Зазвичай ми будемо робити трохи більше роботи, ніж ми зробили в цьому останньому прикладі, щоб вирішити лінійні рівняння, які є результатом використання властивості нульового продукту.
Вирішити:\((5 n-2)(6 n-1)=0\)
- Відповідь
-
\((5 n-2)(6 n-1)=0\) Використовуйте властивість нульового продукту, щоб встановити
кожен коефіцієнт на 0.\(5 n-2=0 \)
\(6 n-1=0\) Розв'яжіть рівняння. \(n=\frac{2}{5}\) \(n = \frac{1}{6}\) Перевірте свої відповіді. 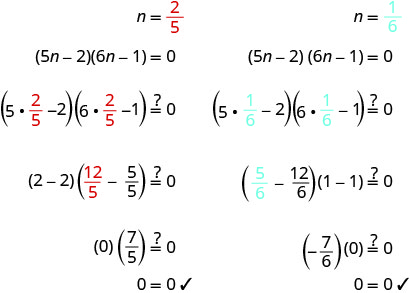
Вирішити:\((3 m-2)(2 m+1)=0\)
- Відповідь
-
\(m=\frac{2}{3}, m=-\frac{1}{2}\)
Вирішити:\((4 p+3)(4 p-3)=0\)
- Відповідь
-
\(p=-\frac{3}{4}, p=\frac{3}{4}\)
Зверніть увагу, коли ми перевірили рішення, що кожен з них зробив лише один коефіцієнт, рівний нулю. Але продукт був нульовим для обох рішень.
Вирішити:\(3 p(10 p+7)=0\)
- Відповідь
-
\(3p(10p+7)=0\) Використовуйте властивість нульового продукту, щоб встановити
кожен коефіцієнт на 0.3p=0 10п+7=0 Розв'яжіть рівняння. p=0 10p=−7 \(p=-\frac{7}{10}\) Перевірте свої відповіді. 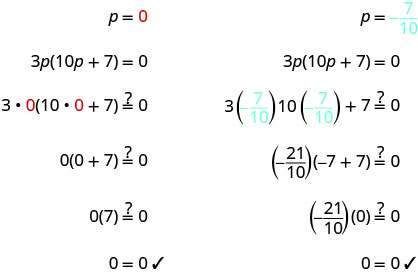
Вирішити:\(2 u(5 u-1)=0\)
- Відповідь
-
\(u=0, u=\frac{1}{5}\)
Вирішити:\(w(2 w+3)=0\)
- Відповідь
-
\(w=0, w=-\frac{3}{2}\)
Може виявитися, що в наступному прикладі є лише один фактор. Пам'ятайте, однак, це\((y-8)^{2}\) означає\((y-8)(y-8)\).
Вирішити:\((y-8)^{2}=0\)
- Відповідь
-
\((y−8)^{2}=0\) Перепишіть ліву сторону як виріб. (y−8) (y−8) =0 Використовуйте властивість нульового продукту та
встановіть для кожного коефіцієнта 0.y−8=0 y−8=0 Розв'яжіть рівняння. y=8 y=8 Коли розчин повторюється, ми називаємо його
подвійним коренем.Перевірте свою відповідь. 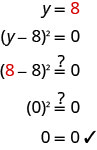
Вирішити:\((x+1)^{2}=0\)
- Відповідь
-
\(x=1\)
Вирішити:\((v-2)^{2}=0\)
- Відповідь
-
\(v=2\)
Розв'язування квадратних рівнянь методом факторингу
Кожне з рівнянь, які ми розв'язали в цьому розділі до цих пір, мали одну сторону в факторованому вигляді. Для того, щоб використовувати властивість нульового продукту, квадратне рівняння має бути враховано з нулем на одній стороні. Тому ми обов'язково почнемо з квадратного рівняння в стандартній формі,\(a x^{2}+b x+c=0\). Потім фактуємо вираз зліва.
Вирішити:\(x^{2}+2 x-8=0\)
- Відповідь
-

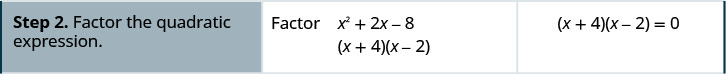



Вирішити:\(x^{2}-x-12=0\)
- Відповідь
-
\(x=4, x=-3\)
Вирішити:\(b^{2}+9 b+14=0\)
- Відповідь
-
\(b=-2, b=-7\)
- Запишіть квадратне рівняння в стандартному вигляді,\(a x^{2}+b x+c=0\).
- Фактор квадратичного виразу.
- Використовуйте властивість нульового продукту.
- Розв'яжіть лінійні рівняння.
- Перевірка.
Перш ніж ми зробимо множник, ми повинні переконатися, що квадратне рівняння знаходиться в стандартній формі.
Вирішити:\(2 y^{2}=13 y+45\)
- Відповідь
-
\(2 y^{2}=13 y+45\) Запишіть квадратне рівняння в стандартному вигляді. \(2 y^{2}-13 y-45=0\) Фактор квадратичного виразу. \((2 y+5)(y-9)=0\) Використовуйте властивість нульового продукту
, щоб встановити кожен коефіцієнт на 0.\(2 y+5=0\) \(y-9=0\) Вирішіть кожне рівняння. \(y=-\frac{5}{2}\) \(y=9\) Перевірте свої відповіді. 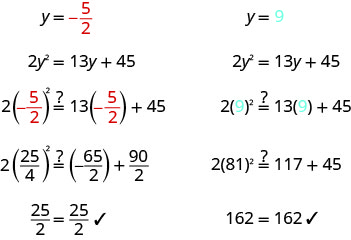
Вирішити:\(3 c^{2}=10 c-8\)
- Відповідь
-
\(c=0, c=\frac{4}{3}\)
Вирішити:\(2 d^{2}-5 d=3\)
- Відповідь
-
\(d=3, d=-\frac{1}{2}\)
Вирішити:\(5 x^{2}-13 x=7 x\)
- Відповідь
-
\(5 x^{2}-13 x=7 x\) Запишіть квадратне рівняння в стандартному вигляді. \(5 x^{2}-20 x=0\) Фактор лівої частини рівняння. \(5 x(x-4)=0\) Використовуйте властивість нульового продукту
, щоб встановити кожен коефіцієнт на 0.\(5x=0\) \(x−4=0\) Вирішіть кожне рівняння. \(x=0\) \(x=4\) Перевірте свої відповіді. 
Вирішити:\(6 a^{2}+9 a=3 a\)
- Відповідь
-
\(a=0, a=-1\)
Вирішити:\(45 b^{2}-2 b=-17 b\)
- Відповідь
-
\(b=0, b=-\frac{1}{3}\)
Вирішення квадратних рівнянь шляхом факторингу буде використовувати всі методи факторингу, які ви дізналися в цьому розділі! Чи розпізнаєте ви спеціальний візерунок продукту в наступному прикладі?
Вирішити:\(144 q^{2}=25\)
- Відповідь
-
\(\begin{array}{lrllrl} & 144 q^{2}&=&25 \\ \text { Write the quadratic equation in standard form. }& 144 q^{2}-25&=& 0 \\ \text { Factor. It is a difference of squares. } & (12 q-5)(12 q+5) & = & 0 \\ \text { Use the Zero Product Property to set each factor to } 0 . & 12 q-5&=&0 & 12 q+5&=&0 \\\text { Solve each equation. } & 12 q & = & 5 & 12 q&=&-5 \\ & q&=&\frac{5}{12} & q & =&-\frac{5}{12} \\ \text { Check your answers. }\end{array}\)
Вирішити:\(25 p^{2}=49\)
- Відповідь
-
\(p=\frac{7}{5}, p=-\frac{7}{5}\)
Вирішити:\(36 x^{2}=121\)
- Відповідь
-
\(x=\frac{11}{6}, x=-\frac{11}{6}\)
Ліва сторона в наступному прикладі враховується, але права сторона не дорівнює нулю. Для того, щоб використовувати властивість нульового продукту, одна сторона рівняння повинна дорівнювати нулю. Ми помножимо множники, а потім запишемо рівняння в стандартній формі.
Вирішити:\((3 x-8)(x-1)=3 x\)
- Відповідь
-
\(\begin{array}{ll} & (3 x-8)(x-1)=3 x \\ \text { Multiply the binomials. }& 3 x^{2}-11 x+8=3 x \\ \text { Write the quadratic equation in standard form. }& 3 x^{2}-14 x+8=0\\ \text { Factor the trinomial. }& (3 x-2)(x-4)=0\\\text { Use the Zero Product Property to set each factor to } 0 . & 3 x-2=0 \quad x-4=0 \\ \text { Solve each equation. } & 3 x=2 \quad x=4 \\ & x=\frac{2}{3} \\ \text { Check your answers. } & \text {The check is left to you! } \end{array}\)
Вирішити:\((2 m+1)(m+3)=12 m\)
- Відповідь
-
\(m=1, m=\frac{3}{2}\)
Вирішити:\((k+1)(k-1)=8\)
- Відповідь
-
\(k=3, k=-3\)
Властивість нульового продукту також застосовується до добутку трьох або більше факторів. Якщо твір дорівнює нулю, хоча б один з факторів повинен дорівнювати нулю. Ми можемо вирішити деякі рівняння ступеня більше двох, використовуючи властивість нульового продукту, так само, як ми розв'язували квадратні рівняння.
Вирішити:\(9 m^{3}+100 m=60 m^{2}\)
- Відповідь
-
\(\begin{array}{lrllrl} & 9 m^{3}+100 m&=&60 m^{2}\\ \text { Bring all the terms to one side so that the other side is zero. } & 9 m^{3}-60 m^{2}+100 m&=&0 \\ \text { Factor the greatest common factor first. } & m\left(9 m^{2}-60 m+100\right)&=&0 \\ \text { Factor the trinomial. } & m(3 m-10)(3 m-10)&=&0 \\ \text { Use the Zero Product Property to set each factor to 0. } & m&=&0 & 3 m-10&=&0 & 3 m-10&=&0 \\ \text { Solve each equation. } & m&=&0 & m&=&\frac{10}{3}& m&=&\frac{10}{3} \\ \text { Check your answers. } & \text { The check is left to you. } \end{array}\)
Вирішити:\(8 x^{3}=24 x^{2}-18 x\)
- Відповідь
-
\(x=0, x=\frac{3}{2}\)
Вирішити:\(16 y^{2}=32 y^{3}+2 y\)
- Відповідь
-
\(y=0, y=\frac{1}{4}\)
Коли ми розрахуємо квадратне рівняння в наступному прикладі, ми отримаємо три множники. Однак першим фактором є постійна. Ми знаємо, що коефіцієнт не може дорівнювати 0.
Вирішити:\(4 x^{2}=16 x+84\)
- Відповідь
-
\(\begin{array}{lrllrl} & 4 x^{2}&=&16 x+84\\ \text { Write the quadratic equation in standard form. }& 4 x^{2}-16 x-84&=&0 \\ \text { Factor the greatest common factor first. }& 4\left(x^{2}-4 x-21\right)&=&0 \\ \text { Factor the trinomial. } & 4(x-7)(x+3)&=&0 \\ \text { Use the Zero Product Property to set each factor to 0. } & 4&\neq&0 & x-7&=&0 & x +3&=&0 \\ \text { Solve each equation. } & 4&\neq&0 & x&=&7& x&=&-3 \\ \text { Check your answers. } & \text { The check is left to you. } \end{array}\)
Вирішити:\(18 a^{2}-30=-33 a\)
- Відповідь
-
\(a=-\frac{5}{2}, a=\frac{2}{3}\)
Вирішити:\(123 b=-6-60 b^{2}\)
- Відповідь
-
\(b=2, b=\frac{1}{20}\)
Розв'язуйте програми, змодельовані квадратними рівняннями
Стратегія розв'язання задач, яку ми використовували раніше для додатків, які перекладають на лінійні рівняння, працюватиме так само добре для додатків, які переводяться на квадратні рівняння. Ми скопіюємо стратегію вирішення проблем тут, щоб ми могли використовувати її для довідки.
- Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі.
- Визначте, що ми шукаємо.
- Назвіть те, що ми шукаємо. Виберіть змінну для представлення цієї кількості.
- Перевести в рівняння. Можливо, буде корисно повторити проблему в одному реченні з усією важливою інформацією. Потім перекладіть англійське речення в рівняння алгебри.
- Вирішіть рівняння, використовуючи хороші методи алгебри.
- Перевірте відповідь в проблемі і переконайтеся, що це має сенс.
- Відповісти на питання повним реченням.
Ми почнемо з числової задачі, щоб отримати практику перекладу слів у квадратне рівняння.
Добуток двох послідовних цілих чисел -\(132 .\) Знайти цілі числа.
- Відповідь
-
\(\begin{array}{ll} \textbf { Step 1. Read} \text { the problem. } \\ \textbf { Step 2. Identify} \text { what we are looking for. } & \text { We are looking for two consecutive integers. } \\ \textbf { Step 3. Name} \text{ what we are looking for. } & \begin{array}{l}{\text { Let } n=\text { the first integer }} \\ {\space n+1=\text { the next consecutive integer }}\end{array} \\\textbf { Step 4. Translate} \text { into an equation. Restate the } & \text { The product of the two consecutive integers is } 132 . \\ \text { problem in a sentence. } \\ \text { Translate to an equation. } & \begin{array}{c}{\text { The first integer times the next integer is } 132 .} \\ {n(n+1)=132}\end{array} \\ \textbf { Step 5. Solve}\text { the equation. } & n^{2}+n=132 \\ \text { Bring all the terms to one side. } & n^{2}+n-132=0 \\ \text { Factor the trinomial. } & (n-11)(n+12)=0 \\ \text { Use the zero product property. } & n-11=0 \quad n+12=0 \\ \text { Solve the equations. } & n=11 \quad n=-12 \end{array}\)
Добуток двох послідовних цілих чисел -\(240 .\) Знайти цілі числа.
- Відповідь
-
\(-15,-16\)і\(15,16\)
Добуток двох послідовних цілих чисел -\(420 .\) Знайти цілі числа.
- Відповідь
-
\(-21,-20\)і\(20,21\)
Ви були здивовані парою від'ємних цілих чисел, яка є одним з рішень попереднього прикладу? Добуток двох натуральних чисел і добуток двох від'ємних цілих чисел дають 132.
У деяких додатках негативні рішення будуть результатом алгебри, але не будуть реалістичними для ситуації.
Прямокутний сад має площу 15 квадратних футів. Довжина саду на два фути більше ширини. Знайдіть довжину і ширину саду.
- Відповідь
-
Крок 1. Прочитайте проблему. У задачах, пов'язаних з геометричними фігурами, начерк може допомогти вам візуалізувати ситуацію. 
Крок 2. Визначте, що ви шукаєте. Шукаємо довжину і ширину. Крок 3. Назвіть те, що ви шукаєте.
Довжина на два фути більше ширини.Нехай W = ширина городу.
W + 2 = довжина садуКрок 4. Перевести в рівняння.
Повторюйте важливу інформацію в реченні.
Площа прямокутного саду становить 15 квадратних футів.Скористайтеся формулою для площі прямокутника. \(A=L \cdot W\) Підставляємо в змінні. \(15=(W+2) W\) Крок 5. Розв'яжіть рівняння. Розподіліть спочатку. \(15=W^{2}+2 W\) Отримайте нуль з одного боку. \(0=W^{2}+2 W-15\) Фактор триноміалу. \(0=(W+5)(W-3)\) Використовуйте властивість нульового продукту. \(0=W+5\) \(0=W−3\) Вирішіть кожне рівняння. \(−5=W\) \(3=W\) Так як W - ширина саду, для
неї немає сенсу бути
негативним. Ми усуваємо це значення для W.\(W=−5\) cannot be the width, since it's negative.
\(W=3\)\(3=W\)
Ширина - 3 фути.Знайти значення довжини. \(\text{length}=W+2\) \(\text{length}=3+2\) \(\text{length}=5\) Довжина - 5 футів. Крок 6. Перевірте відповідь.
Чи має сенс відповідь?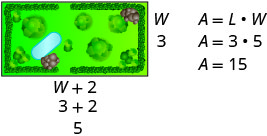
Так, в цьому є сенс. Крок 7. Дайте відповідь на питання. Ширина саду становить 3 фути,
а довжина - 5 футів.
Прямокутний знак має площу 30 квадратних футів. Довжина знака на одну ногу більше ширини. Знайдіть довжину і ширину знака.
- Відповідь
-
55 футів і 66 футів
Прямокутний внутрішній дворик має площу 180 квадратних футів. Ширина внутрішнього дворика на три фути менше довжини. Знайдіть довжину і ширину патіо.
- Відповідь
-
12 футів і 15 футів
У попередньому розділі ми використовували теорему Піфагора\(\left(a^{2}+b^{2}=c^{2}\right)\). Це дало відношення між катетами і гіпотенузою прямокутного трикутника.
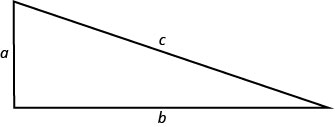
Ми будемо використовувати цю формулу в наступному прикладі.
Жюстін хоче поставити колоду в кутку свого заднього двору у формі прямокутного трикутника, як показано нижче. Гіпотенуза буде довжиною 17 футів. Довжина однієї сторони буде на 7 футів менше довжини іншої сторони. Знайдіть довжини сторін колоди.
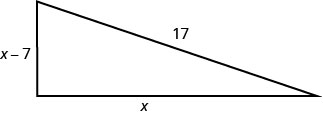
- Відповідь
-
Крок 1. Прочитайте проблему. Крок 2. Визначте, що ви шукаєте. Шукаємо довжини сторін
колоди.Крок 3. Назвіть те, що ви шукаєте.
Одна сторона на 7 менше, ніж інша.Нехай x = довжина сторони палуби
x − 7 = довжина іншої сторониКрок 4. Перевести в рівняння.
Оскільки це прямокутний трикутник, ми можемо використовувати
теорему Піфагора.\(a^{2}+b^{2}=c^{2}\) Підставляємо в змінні. \(x^{2}+(x-7)^{2}=17^{2}\) Крок 5. Розв'яжіть рівняння. \(x^{2}+x^{2}-14 x+49=289\) Спростити. \(2 x^{2}-14 x+49=289\) Це квадратне рівняння, тому отримайте нуль з одного боку. \(2 x^{2}-14 x-240=0\) Фактор найбільший загальний фактор. \(2\left(x^{2}-7 x-120\right)=0\) Фактор триноміалу. \(2(x-15)(x+8)=0\) Використовуйте властивість нульового продукту. \(2\neq 0\) \(x−15=0\) \(x+8=0\) Вирішити. \(2\neq 0\) \(x=15\) \(x=-8\) Так як\(x\) це сторона трикутника,\(x=−8\) не має
сенсу.\(2\neq 0\) \(x=15\) \(\cancel{x=−8}\) Знайдіть довжину іншої сторони. Якщо довжина однієї сторони дорівнює \(x=15\) то довжина іншої сторони дорівнює \(x-7\) \(15 - 7 = 8\) 8 - довжина іншої сторони. Крок 6. Перевірте відповідь.
Чи мають сенс ці цифри?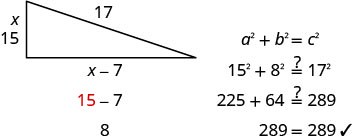
Крок 7. Дайте відповідь на питання. Сторони палуби - 8, 15 і 17 футів.
Вітрило човна - це прямокутний трикутник. Довжина однієї сторони вітрила на 7 футів більше, ніж інша сторона. Гіпотенуза дорівнює 13. Знайдіть довжини двох сторін вітрила.
- Відповідь
-
5 футів і 12 футів
Сад медитації має форму прямокутного трикутника, з однією ногою 7 футів. Довжина гіпотенузи на один більше довжини одного з інших катетів. Знайти довжини гіпотенузи і іншого катета.
- Відповідь
-
24 фути і 25 футів
Ключові поняття
- Нульовий продукт Властивість Якщо\(a \cdot b=0\), то або a=0 або b=0 або обидва. Див. Приклад.
- Вирішити квадратне рівняння шляхом факторингу Вирішити квадратне рівняння факторингом: Див. Приклад.
- Запишіть квадратне рівняння в стандартному вигляді,\(a x^{2}+b x+c=0\).
- Фактор квадратичного виразу.
- Використовуйте властивість нульового продукту.
- Розв'яжіть лінійні рівняння.
- Перевірка.
- Використовуйте стратегію вирішення проблем для вирішення проблем зі словами Див. Приклад.
- Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі.
- Визначте, що ми шукаємо.
- Назвіть те, що ми шукаємо. Виберіть змінну для представлення цієї кількості.
- Перевести в рівняння. Можливо, буде корисно повторити проблему в одному реченні з усією важливою інформацією. Потім перекладіть англійське речення в рівняння алгебри.
- Вирішіть рівняння, використовуючи хороші методи алгебри.
- Перевірте відповідь в проблемі і переконайтеся, що це має сенс.
- Відповісти на питання повним реченням.
Глосарій
- квадратні рівняння
- є рівняннями, в яких змінна знаходиться в квадраті.
- Нульова властивість продукту
- Властивість нульового продукту стверджує, що якщо добуток двох величин дорівнює нулю, принаймні одна з величин дорівнює нулю.
