7.6E: Вправи

Last updated
Save as PDF

Page ID: 58754

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Практика робить досконалим

Використовувати властивість нульового продукту

У наступних вправах вирішуйте.

Вправа 1

$(x−3)(x+7)=0$

Відповідь: $x=3$,$x=−7$ Таким чином, набір рішень:$\{3, -7\}$

Вправа 2

$(y−11)(y+1)=0$

Вправа 3

$(3a−10)(2a−7)=0$

Відповідь: $a=\frac{10}{3}$,$a=\frac{7}{2}$ Таким чином, набір рішень:$\Big\{\tfrac{10}{3}, \tfrac{7}{2}\Big\}$

Вправа 4

$(5b+1)(6b+1)=0$

Вправа 5

$6m(12m−5)=0$

Відповідь: $m=0$,$m=\frac{5}{12}$ Таким чином, набір рішень:$\Big\{0, \tfrac{5}{12}\Big\}$

Вправа 6

$2x(6x−3)=0$

Вправа 7

$(y−3)^2=0$

Відповідь: $y=3$Отже, набір рішень:$\{3\}$

Вправа 8

$(b+10)^2=0$

Вправа 9

$(2x−1)^2=0$

Відповідь: $x=\frac{1}{2}$Отже, набір рішень:$\Big\{\tfrac{1}{2}\Big\}$

Вправа 10

$(3y+5)^2=0$

Розв'язування квадратних рівнянь методом факторингу

У наступних вправах вирішуйте.

Вправа 11

$x^2+7x+12=0$

Відповідь: $x=−3$,$x=−4$ Таким чином, набір рішень:$\{-3, -4\}$

Вправа 12

$y^2−8y+15=0$

Вправа 13

$5a^2−26a=24$

Відповідь: $a=−\tfrac{4}{5}$,$a=6$ Таким чином, набір рішень:$\Big\{−\tfrac{4}{5}, 6\Big\}$

Вправа 14

$4b^2+7b=−3$

Вправа 15

$4m^2=17m−15$

Відповідь: $m=\frac{5}{4}$,$m=3$ Таким чином, набір рішень:$\Big\{\tfrac{5}{4}, 3\Big\}$

Вправа 16

$n^2=5−6n$

Вправа 17

$7a^2+14a=7a$

Відповідь: $a=−1$,$a=0$ Таким чином, набір рішень:$\{-1, 0\}$

Вправа 18

$12b^2−15b=−9b$

Вправа 19

$49m^2=144$

Відповідь: $m=\frac{12}{7}$,$m=−\frac{12}{7}$ Таким чином, набір рішень:$\Big\{−\tfrac{12}{7}, \tfrac{12}{7}\Big\}$

Вправа 20

$625=x^2$

Вправа 21

$(y−3)(y+2)=4y$

Відповідь: $y=−1$,$y=6$ Таким чином, набір рішень:$\{-1, 6\}$

Вправа 22

$(p−5)(p+3)=−7$

Вправа 23

$(2x+1)(x−3)=−4x$

Відповідь: $x=\frac{3}{2}$,$x=−1$ Таким чином, набір рішень:$\Big\{-1,\tfrac{3}{2}\Big\}$

Вправа 24

$(x+6)(x−3)=−8$

Вправа 25

$16p^3=24p^2−9p$

Відповідь: $p=0$,$p=\frac{3}{4}$ Таким чином, набір рішень:$\Big\{0,\tfrac{3}{4}\Big\}$

Вправа 26

$m^3−2m^2=−m$

Вправа 27

$20x^2−60x=−45$

Відповідь: $x=\frac{3}{2}$Отже, набір рішень:$\Big\{\tfrac{3}{2}\Big\}$

Вправа 28

$3y^2−18y=−27$

Розв'язуйте програми, змодельовані квадратними рівняннями

У наступних вправах вирішуйте.

Вправа 29

Добуток двох послідовних цілих чисел дорівнює 56. Знайти цілі числа.

Відповідь: 7 і 8; −8 і −7

Вправа 30

Добуток двох послідовних цілих чисел дорівнює 42. Знайти цілі числа.

Вправа 31

Площа прямокутного килима становить 28 квадратних футів. Довжина на три фути більше ширини. Знайдіть довжину і ширину килима.

Відповідь: 4 фути і 7 футів

Вправа 32

Прямокутна підпірна стіна має площу 15 квадратних футів. Висота стіни на два фути менше її довжини. Знайдіть висоту і довжину стіни.

Вправа 33

Вимпел має форму прямокутного трикутника, з гіпотенузою 10 футів. Довжина однієї сторони вимпела на два фути більше довжини іншої сторони. Знайдіть довжину двох сторін вимпела.

Відповідь: 6 футів і 8 футів

Вправа 34

Басейн, що відбиває, має форму прямокутного трикутника, з однією ніжкою вздовж стіни будівлі. Гіпотенуза на 9 футів довша за сторону вздовж будівлі. Третя сторона на 7 футів довша, ніж сторона вздовж будівлі. Знайдіть довжини всіх трьох сторін відбиває басейну.

Змішана практика

У наступних вправах вирішуйте.

Вправа 35

(х+8) (х−3) =0

Відповідь: $x=−8, \; x=3$Отже, набір рішень:$\{-8, 3\}$

Вправа 36

(3й−5) (y+7) =0

Вправа 37

$p^2+12p+11=0$

Відповідь: $p=−1, \;p=−11$Отже, набір рішень:$\{-11, -1\}$

Вправа 38

$q^2−12q−13=0$

Вправа 39

$m^2=6m+16$

Відповідь: $m=−2, \; m=8$Отже, набір рішень:$\{-2, 8\}$

Вправа 40

$4n^2+19n=5$

Вправа 41

$a^3−a^2−42a=0$

Відповідь: $a=0, \;a=−6, \;a=7$Отже, набір рішень:$\{-6, 0, 7\}$

Вправа 42

$4b^2−60b+224=0$

Вправа 43

Добуток двох послідовних цілих чисел дорівнює 110. Знайти цілі числа.

Відповідь: 10 і 11; −11 і −10

Вправа 44

Довжина однієї ніжки прямокутного трикутника на три більше, ніж іншої ноги. Якщо гіпотенуза дорівнює 15, знайдіть довжини двох катетів.

Щоденна математика

Вправа 45

Площа внутрішнього дворика Якщо кожна сторона квадратного внутрішнього дворика збільшена на 4 фути, площа внутрішнього дворика становила б 196 квадратних футів. Розв'яжіть рівняння (s+4) 2=196 (s+4) 2=196 для s, щоб знайти довжину сторони внутрішнього дворика.

Відповідь: 10 футів

Вправа 46

Кавунова крапля Кавун скидається з десятого поверху будівлі. Розв'яжіть рівняння −16t2+144=0−16t2+144=0, щоб tt знайшов кількість секунд, які потрібно кавуну, щоб досягти землі.

Письмові вправи

Вправа 47

Поясніть, як ви вирішуєте квадратне рівняння. Скільки відповідей ви очікуєте отримати для квадратного рівняння?

Відповідь: Відповіді можуть відрізнятися для пояснення. Для квадратного рівняння слід очікувати не більше 2 розв'язків. Часто він має два рішення, але іноді, він може мати один повторний розчин або навіть не розчин.

Вправа 48

Наведіть приклад квадратного рівняння, яке має GCF і жоден з розв'язків рівняння не дорівнює нулю.

Самостійна перевірка

а Після виконання вправ скористайтеся цим контрольним списком, щоб оцінити своє володіння цілями цього розділу.

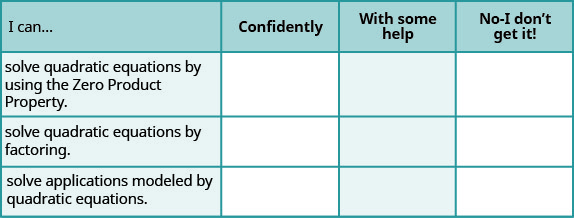
$Ця таблиця має наступні твердження, яким передує «Я можу...». Перший рядок - «вирішити квадратні рівняння за допомогою властивості нульового добутку». Другий рядок - «вирішити квадратні рівняння шляхом факторингу». Третій рядок - «вирішувати додатки, змодельовані квадратними рівняннями». У стовпцях поруч із цими твердженнями знаходяться заголовки, «впевнено», «з деякою допомогою» та «Ні-я не розумію!».$

б Загалом, подивившись контрольний список, ви вважаєте, що добре підготовлені до наступного розділу? Чому чи чому ні?