2.5: Квадратні рівняння
- Page ID
- 59239
- Розв'яжіть квадратні рівняння методом факторингу.
- Розв'яжіть квадратні рівняння за властивістю квадратного кореня.
- Вирішіть квадратні рівняння, заповнивши квадрат.
- Розв'яжіть квадратні рівняння за допомогою квадратичної формули.
Монітор комп'ютера зліва на малюнку\(\PageIndex{1}\)\(23.6\) - це дюймова модель, а праворуч\(27\) - дюймова модель. Пропорційно монітори виглядають дуже схожими. Якщо є обмежена кількість простору, і ми хочемо якомога більшого монітора, як ми вирішуємо, який вибрати? У цьому розділі ми дізнаємося, як вирішити такі проблеми, як ця, використовуючи чотири різні методи.

Розв'язування квадратних рівнянь методом факторингу
Рівняння, що містить многочлен другого ступеня, називається квадратним рівнянням. Наприклад, рівняння, такі як\(2x^2 +3x−1=0\) і\(x^2−4= 0\) є квадратними рівняннями. Вони використовуються незліченними способами в областях інженерії, архітектури, фінансів, біологічних наук і, звичайно ж, математики.
Часто найпростішим методом розв'язання квадратного рівняння є факторинг. Факторинг означає знаходження виразів, які можна помножити разом, щоб дати вираз на одній стороні рівняння.
Якщо квадратне рівняння може бути враховано, воно записується як добуток лінійних членів. Розв'язування факторингом залежить від властивості нульового добутку, в якому зазначено\(a⋅b=0\), що if\(b =0\), то\(a = 0\) або, де a і b - дійсні числа або алгебраїчні вирази. Іншими словами, якщо добуток двох чисел або двох виразів дорівнює нулю, то одне з чисел або одне з виразів має дорівнювати нулю, оскільки нуль помножений на що-небудь дорівнює нулю.
Множення коефіцієнтів розширює рівняння до рядка членів, розділених знаками плюс або мінус. Отже, в цьому сенсі операція множення скасовує операцію факторингу. Наприклад, розгорніть факторний вираз,\((x−2)(x+3)\) множивши два множники разом.
\[\begin{align*} (x-2)(x+3)&= x^2+3x-2x-6\\ &= x^2+x-6\\ \end{align*}\]
Твір являє собою квадратичний вираз. Встановлено рівне нулю,\(x^2+x−6= 0\) являє собою квадратне рівняння. Якби ми мали коефіцієнт рівняння, ми б повернули множники.
Процес факторингу квадратного рівняння залежить від провідного коефіцієнта, будь він\(1\) або інше ціле число. Ми розглянемо обидві ситуації; але спочатку хочемо підтвердити, що рівняння записано в стандартній формі, де\(ax^2+bx+c=0\)\(a\)\(b\), і\(c\) є дійсними числами, і\(a≠0\). Рівняння\(x^2 +x−6= 0\) знаходиться в стандартній формі.
Ми можемо використовувати властивість нульового добутку для вирішення квадратних рівнянь, в яких ми спочатку повинні перерахувати найбільший загальний коефіцієнт (GCF), а також для рівнянь, які мають спеціальні формули факторингу, такі як різниця квадратів, обидва з яких ми побачимо пізніше в цьому розділі.
Властивість нульового продукту
Якщо\(a⋅b=0\), то\(a=0\) або\(b=0\),
де\(a\) і\(b\) дійсні числа або алгебраїчні вирази.
Квадратне рівняння - це рівняння, що містить многочлен другого ступеня; наприклад
\[ax^2+bx+c=0\]
де\(a\)\(b\), і\(c\) є дійсними числами, а якщо\(a≠0\), то в стандартному вигляді.
Розв'язування квадратики з провідним коефіцієнтом\(1\)
У квадратному\(x^2 +x−6=0\) рівнянні провідним коефіцієнтом, або коефіцієнтом\(x^2\), є\(1\). Ми маємо один метод факторингу квадратних рівнянь у такому вигляді.
- Знайдіть два числа, добуток яких дорівнює,\(c\) а сума яких дорівнює\(b\).
- Використовуйте ці числа, щоб записати два множники виду\((x+k)\) або\((x−k)\), де k - одне з чисел, знайдених на кроці 1. Використовуйте цифри точно такими, якими вони є. Іншими словами, якщо два числа\(1\) і\(−2\), фактори є\((x+1)(x−2)\).
- Вирішіть, використовуючи властивість нульового добутку, встановивши кожен коефіцієнт рівний нулю та вирішуючи для змінної.
Коефіцієнт і вирішуємо рівняння:\(x^2+x−6=0\).
Рішення
Для\(x^2 +x−6=0\) множника ми шукаємо два числа, добуток яких дорівнює\(−6\) і сума яких дорівнює\(1\). Почніть з розгляду можливих факторів\(−6\).
\[1⋅(−6) \nonumber \]
\[(−6)⋅1 \nonumber \]
\[2⋅(−3) \nonumber \]
\[3⋅(−2) \nonumber \]
Остання пара,\(3⋅(−2)\) сума до\(1\), так що це числа. Зверніть увагу, що працювати буде тільки одна пара чисел. Потім напишіть фактори.
\[(x−2)(x+3)=0 \nonumber \]
Для вирішення цього рівняння використовуємо властивість нульового добутку. Встановіть кожен коефіцієнт рівним нулю і вирішуйте.
\[\begin{align*} (x-2)(x+3)&= 0\\ (x-2)&= 0\\ x&= 2\\ (x+3)&= 0\\ x&= -3 \end{align*}\]
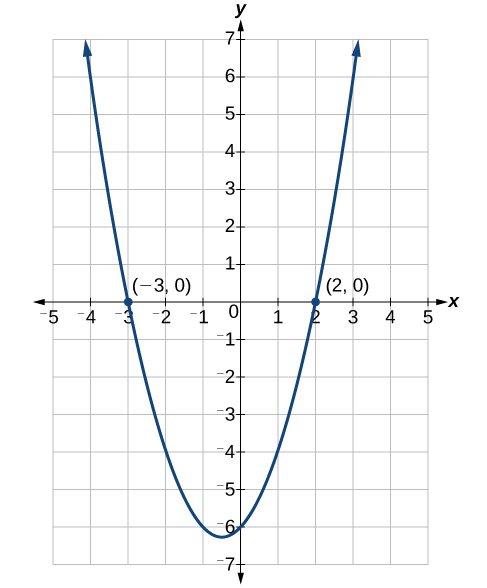
Два рішення - це\(2\) і\(−3\). Ми бачимо, як розв'язки пов'язані з графіком на малюнку\(\PageIndex{2}\). Рішення є х-перехоплення\(x^2 +x−6=0\).
Коефіцієнт і розв'яжіть квадратне рівняння:\(x^2−5x−6=0\).
- Відповідь
-
\((x−6)(x+1)=0\),\(x=6\),\(x=−1\)
Розв'яжіть квадратне рівняння шляхом факторингу:\(x^2+8x+15=0\).
Рішення
Знайдіть два числа, добуток яких дорівнює,\(15\) а сума яких дорівнює\(8\). Перерахуйте фактори\(15\).
\[1⋅15 \nonumber \]
\[3⋅5 \nonumber \]
\[(−1)⋅(−15) \nonumber \]
\[(−3)⋅(−5) \nonumber \]
Числа, які\(8\) додаються до є\(3\) і\(5\). Потім запишіть множники, встановіть кожен коефіцієнт рівним нулю, і вирішіть.
\[\begin{align*} (x+3)(x+5)&= 0\\ (x+3)&= 0\\ x&= -3\\ (x+5)&= 0\\ x&= -5 \end{align*}\]
Рішення є\(−3\) і\(−5\).
Розв'яжіть квадратне рівняння шляхом факторингу:\(x^2−4x−21=0\).
- Відповідь
-
\((x−7)(x+3)=0\),\(x=7\),\(x=−3\)
Розв'яжіть рівняння різниці квадратів за допомогою властивості нульового добутку:\(x^2−9=0\).
Рішення
Визнаючи, що рівняння являє собою різницю квадратів, ми можемо записати два множники, взявши квадратний корінь кожного члена, використовуючи знак мінус як оператор в одному множнику і знак плюс як оператор в іншому. Вирішіть за допомогою властивості нульового фактора.
\[\begin{align*} x^2-9&= 0\\ (x-3)(x+3)&= 0\\ x-3&= 0\\ x&= 3\\ (x+3)&= 0\\ x&= -3 \end{align*}\]
Рішення є\(3\) і\(−3\).
Вирішити факторингом:\(x^2−25=0\).
- Відповідь
-
\((x+5)(x−5)=0, x=−5, x=5\)
Факторинг та розв'язування квадратного рівняння вищого порядку
Коли провідного коефіцієнта немає\(1\), ми множимо квадратне рівняння за допомогою методу, який називається групуванням, який вимагає чотирьох членів.
З рівнянням в стандартній формі розглянемо процедури групування
- При квадратичному в стандартному вигляді\(ax^2+bx+c=0\), помножте\(a⋅c\).
- Знайдіть два числа, добуток яких дорівнює ac, а сума яких дорівнює\(b\).
- Перепишіть рівняння, замінивши\(bx\) термін на два члени, використовуючи числа, знайдені в ступені\(1\), як коефіцієнти\(x\).
- Фактор перших двох членів, а потім множник останніх двох термінів. Вирази в дужках повинні бути точно такими ж, щоб використовувати групування.
- Фактор виразу в дужках.
- Встановіть вирази, рівні нулю, і вирішіть для змінної.
Використовуйте групування для множника та розв'яжіть квадратне рівняння:\(4x^2+15x+9=0\).
Рішення
По-перше, помножте\(ac:4(9)=36\). Потім перерахуйте фактори\(36\).
\[1⋅36 \nonumber\]
\[2⋅18 \nonumber\]
\[3⋅12 \nonumber\]
\[4⋅9 \nonumber\]
\[6⋅6 \nonumber\]
Єдина пара факторів, яка\(15\) становить це\(3+12\). Перепишіть рівняння, що замінює члену b\(15x\), з двома термінами, використовуючи\(3\) і\(12\) як коефіцієнти\(x\). Порахуйте перші два терміни, а потім множник останніх двох термінів.
\[\begin{align*} 4x^2+3x+12x+9&= 0\\ x(4x+3)+3(4x+3)&= 0\\ (4x+3)(x+3)&= 0 \qquad \text{Solve using the zero-product property}\\ (4x+3)&= 3\\ x&= -\dfrac{3}{4}\\ (x+3)&= 0\\ x&= -3 \end{align*}\]
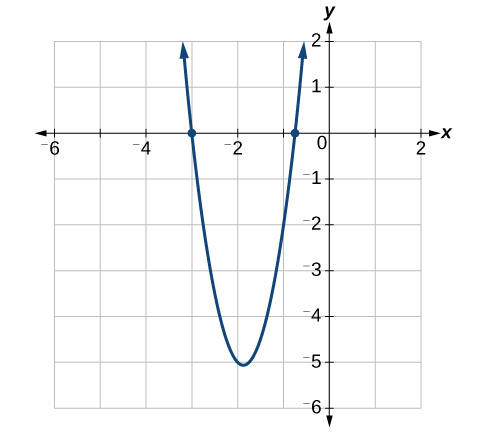
Рішення є\(−\dfrac{3}{4}\), і\(−3\). Див\(\PageIndex{3}\). Малюнок.
Вирішити за допомогою факторингу шляхом групування:\(12x^2+11x+2=0\).
- Відповідь
-
\((3x+2)(4x+1)=0\),\(x=−\dfrac{2}{3}\),\(x=−\dfrac{1}{4}\)
Вирішити рівняння шляхом факторингу:\(−3x^3−5x^2−2x=0\).
Рішення
Це рівняння не виглядає квадратичним, як найвища потужність\(3\), ні\(2\). Нагадаємо, що перше, що ми хочемо зробити при вирішенні будь-якого рівняння - це перерахувати GCF, якщо він існує. І це відбувається тут. Ми можемо врахувати\(−x\) з усіх термінів, а потім приступити до групування.
\ [\ begin {align*}
-3x^3-5x^2-2x&= 0\\
-x (3x^2+5x+2) &= 0\\
-x (3x^2+3x+2x+2) &= 0\ qquad\ text {Використовуйте групування виразу в дужках}\\
-x [3x (x+1) +2 (x+1)] &= 0\\
-x (3x+2) (x+1) &= 0
\\\ текст {Тепер ми використовуємо властивість нульового продукту. Зверніть увагу, що ми маємо три фактори.} \\
-x&= 0\\
x&= 0\\
3х+2&= 0\\
x&= -\ dfrac {2} {3}\\
x+1&= 0\\
x&= -1
\\ кінець {вирівнювати*}\]
Рішення є\(0\)\(−\dfrac{2}{3}\), і\(−1\).
Вирішити факторингом:\(x^3+11x^2+10x=0\).
- Відповідь
-
\(x=0, x=−10, x=−1\)
Використання властивості квадратного кореня
Коли в рівнянні немає лінійного члена, іншим методом вирішення квадратного рівняння є використання властивості квадратного кореня, в якому ми виділимо\(x^2\) член і беремо квадратний корінь числа на іншій стороні знака рівності. Майте на увазі, що іноді нам, можливо, доведеться маніпулювати рівнянням, щоб виділити\(x^2\) термін, щоб можна було використовувати властивість квадратного кореня.
При виділеному\(x^2\) терміні властивість квадратного кореня стверджує, що:
де\(k\) - ненульове дійсне число.
- Виділяють\(x^2\) термін з одного боку від знака рівності.
- Візьміть квадратний корінь обох сторін рівняння, поставивши\(±\) знак перед виразом на стороні, протилежній квадратному члену.
- Спростити цифри збоку зі\(±\) знаком.
Вирішіть квадратичну, використовуючи властивість квадратного кореня:\(x^2=8\).
Рішення
Візьміть квадратний корінь з обох сторін, а потім спростіть прикорінний. Не забудьте використовувати\(±\) знак перед радикальним символом.
\[\begin{align*} x^2&= 8\\ x&= \pm \sqrt{8}\\ &= \pm 2\sqrt{2} \end{align*}\]
Рішення є\(2\sqrt{2}\),\(-2\sqrt{2}\)
Розв'яжіть квадратне рівняння:\(4x^2+1=7\).
Рішення
По-перше, виділіть\(x^2\) термін. Потім візьміть квадратний корінь з обох сторін.
\[\begin{align*} 4x^2+1&= 7\\ 4x^2&= 6\\ x^2&= \dfrac{6}{4}\\ x&= \pm \dfrac{\sqrt{6}}{2} \end{align*}\]
Рішення є\(\dfrac{\sqrt{6}}{2}\), і\(-\dfrac{\sqrt{6}}{2}\).
Розв'яжіть квадратне рівняння, використовуючи властивість квадратного кореня:\(3{(x−4)}^2=15\).
- Відповідь
-
\(x=4±\sqrt{5}\)
Завершення площі
Не всі квадратні рівняння можуть бути враховані або можуть бути вирішені в первісному вигляді за допомогою властивості квадратного кореня. У цих випадках ми можемо використовувати метод розв'язання квадратного рівняння, відомого як завершення квадрата. Використовуючи цей метод, ми додаємо або віднімаємо члени до обох сторін рівняння, поки не отримаємо досконалий квадратний триноміал на одній стороні знака рівності. Потім ми застосовуємо властивість квадратного кореня. Для завершення квадрата провідний коефіцієнт\(a\), повинен дорівнювати\(1\). Якщо його немає, то ділимо все рівняння на\(a\). Потім ми можемо використовувати наступні процедури для вирішення квадратного рівняння, заповнивши квадрат.
Ми будемо використовувати приклад\(x^2+4x+1=0\) для ілюстрації кожного кроку.
Задано квадратне рівняння, яке не може бути враховано, і з\(a=1\), first add or subtract the constant term to the right sign of the equal sign.
\ [\ begin {align*}
x^2+4x+1&= 0\\
x^2+4x&= -1\ qquad\ text {Помножте b}\ текст {термін на}\ dfrac {1} {2}\ text {і квадрат його.} \\
\ dfrac {1} {2} (4) &= 2\\
2^2&= 4\ qquad\ text {Додати}\ left ({\ dfrac {1} {2}}\ право) ^2\ text {до обох сторін знака рівності і спростити праву сторону. У нас є}\
x^2+4x+4&= -1+4\\
x^2+4x+4&= 3\ qquad\ text {Ліву частину рівняння тепер можна розглядати як ідеальний квадрат.} \\
{(x+2)} ^2&=3\
\ sqrt {{(x+2)} ^2} &=\ pm\ sqrt {3}\ qquad\ text {Використовуйте властивість квадратного кореня та розв'яжіть.} \\
\ sqrt {{(x+2)} ^2} &=\ пм\ sqrt {3}\\
x+2&=\ pm\ sqrt {3}\\
x&= -2\ pm\ sqrt {3}
\ end {align*}\]
Рішення є\(−2+\sqrt{3}\), і\(−2−\sqrt{3}\).
Вирішіть квадратне рівняння, заповнивши квадрат:\(x^2−3x−5=0\).
Рішення
Спочатку перемістіть постійний член в праву сторону знака рівності.
\ [\ begin {align*}
x^2-3x&= 5\ qquad\ text {Потім візьміть}\ dfrac {1} {2}\ text {з b терміна і квадрат його.} \\
\ dfrac {1} {2} (-3) &= -\ dfrac {3} {2}\\
ліворуч (-\ dfrac {3} {2}\ праворуч)} ^2=\ dfrac {9} {4}\
x^2-3x+ {\ ліворуч (-\ dfrac {3} {2}\ праворуч)} ^2&= 5&= + {\ left (-\ dfrac {3} {2}\ справа)} ^2\ qquad\ text {Додати результат до обох сторін знака рівності.} \\
x^2-3x+\ dfrac {9} {4} &= 5+\ dfrac {9} {4}\
\ text {Вкажіть ліву сторону як ідеальний квадрат і спростіть праву сторону.} \\
{\ ліворуч (x-\ dfrac {3} {2}\ праворуч)} ^2&=\ dfrac {29} {4}\
(x-\ dfrac {3} {2}) &=\ pm\ dfrac {\ sqrt {29}} {2}\ qquad\ text {Використовуйте властивість квадратного кореня та вирішуйте.} \\
x&=\ dfrac {3} {2}\ пм\ dfrac {\ sqrt {29}} {2}\
\ end {align*}\]
Рішення є\(\dfrac{3}{2}+\dfrac{\sqrt{29}}{2}\), і\(\dfrac{3}{2}-\dfrac{\sqrt{29}}{2}\)
Вирішіть, заповнивши квадрат:\(x^2−6x=13\).
- Відповідь
-
\(x=3±\sqrt{22}\)
Використання квадратичної формули
Четвертий метод вирішення квадратного рівняння полягає в використанні квадратної формули, формули, яка вирішить всі квадратні рівняння. Хоча квадратична формула працює на будь-якому квадратному рівнянні в стандартній формі, легко зробити помилки при підстановці значень у формулу. Зверніть пильну увагу при заміні, і використовуйте дужки при вставці негативного числа.
Ми можемо вивести квадратичну формулу, заповнивши квадрат. Будемо вважати, що провідний коефіцієнт позитивний; якщо він\(ax^2+bx+c=0, a≠0\) від'ємний, ми можемо помножити рівняння на\(−1\) і отримати позитивне a.
Спочатку перенесіть постійний член в праву сторону знака рівності:
\[ax^2+bx=−c \nonumber \]
Оскільки ми хочемо, щоб провідний коефіцієнт\(1\) дорівнював, ділимо через\(a\):
\[x^2+\dfrac{b}{a}x=−\dfrac{c}{a} \nonumber \]
Потім знайдіть\(\dfrac{1}{2}\) середній член і додайте\({(\dfrac{1}{2}\dfrac{b}{a})}^2=\dfrac{b^2}{4a^2}\) до обох сторін знак рівності:
\[x^2+\dfrac{b}{a}x+\dfrac{b^2}{4a^2}=\dfrac{b^2}{4a^2}-\dfrac{c}{a} \nonumber \]
Далі напишіть ліву сторону як ідеальний квадрат. Знайдіть спільний знаменник правого боку і запишіть його як одиничний дріб:
\[{(x+\dfrac{b}{2a})}^2=\dfrac{b^2-4ac}{4a^2} \nonumber \]
Тепер використовуйте властивість квадратного кореня, яка дає
\[x+\dfrac{b}{2a}=±\sqrt{\dfrac{b^2-4ac}{4a^2}} \nonumber \]
\[x+\dfrac{b}{2a}=\dfrac{±\sqrt{b^2-4ac}}{2a} \nonumber \]
Нарешті, додайте\(-\dfrac{b}{2a}\) до обох сторін рівняння і об'єднайте члени з правого боку. Таким чином,
\[x=\dfrac{-b±\sqrt{b^2-4ac}}{2a} \nonumber \]
Записане в стандартній формі\(ax^2+bx+c=0\), будь-яке квадратне рівняння може бути вирішено за допомогою квадратичної формули:
\[x=\dfrac{-b±\sqrt{b^2-4ac}}{2a}\]де\(a\)\(b\), і\(c\) є дійсними числами і\(a≠0\).
Задано квадратне рівняння, розв'яжіть його за квадратичною формулою
- Переконайтеся, що рівняння має стандартну форму:\(ax^2+bx+c=0\).
- Зверніть увагу на значення коефіцієнтів і постійний член,\(a\),\(b\), і\(c\).
- Обережно підставляємо значення, зазначені на кроці 2, в рівняння. Щоб уникнути зайвих помилок, використовуйте круглі дужки навколо кожного числа, введеного у формулу.
- Розрахувати і вирішити.
Розв'яжіть квадратне рівняння:\(x^2+5x+1=0\).
Рішення
Визначте коефіцієнти:\(a=1,b=5,c=1\). Потім використовуйте квадратичну формулу.
\[\begin{align*} x&= \dfrac{-(5) \pm \sqrt{(5)^2-4(1)(1)}}{2(1)}\\ &= \dfrac{-5 \pm \sqrt{25-4}}{2}\\ &= \dfrac{-5 \pm \sqrt{21}}{2} \end{align*}\]
Використовуйте квадратичну формулу для вирішення\(x^2+x+2=0\).
Рішення
Спочатку виділимо коефіцієнти:\(a=1\),\(b=1\), і\(c=2\).
Підставляємо ці значення в квадратичну формулу.
\[\begin{align*} x&= \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}\\ &= \dfrac{-(1) \pm \sqrt{(1)^2-4(1)(2)}}{2(1)}\\ &= \dfrac{-1 \pm \sqrt{1-8}}{2}\\ &= \dfrac{-1 \pm \sqrt{-7}}{2}\\ &= \dfrac{-1 \pm i\sqrt{7}}{2} \end{align*}\]
Розв'яжіть квадратне рівняння, використовуючи квадратичну формулу:\(9x^2+3x−2=0\).
- Відповідь
-
\(x=-\dfrac{2}{3},x=\dfrac{1}{3}\)
Дискримінант
Квадратична формула не тільки генерує розв'язки квадратного рівняння, вона розповідає нам про природу розв'язків, коли ми розглядаємо дискримінант, або вираз під радикалом\(b^2−4ac\). Дискримінант говорить нам, чи є розв'язки дійсними числами чи комплексними числами, і скільки розв'язків кожного типу слід очікувати. Таблиця\(\PageIndex{1}\) пов'язує значення дискримінанту з розв'язками квадратного рівняння.
| Значення дискримінанту | Результати |
|---|---|
| \(b^2−4ac=0\) | Одне раціональне рішення (подвійне рішення) |
| \(b^2−4ac>0\), ідеальний квадрат | Два раціональних рішення |
| \(b^2−4ac>0\), не ідеальний квадрат | Два нераціональних рішення |
| \(b^2−4ac<0\) | Два комплексних рішення |
Для\(ax^2+bx+c=0\), де\(a\)\(b\), і\(c\) є дійсними числами, дискримінант - це вираз під радикалом в квадратичній формулі:\(b^2−4ac\). Він говорить нам про те, чи є розв'язки дійсними числами чи комплексними числами і скільки розв'язків кожного типу слід очікувати.
Використовуйте дискримінант, щоб знайти характер розв'язків наступних квадратичних рівнянь:
- \(x^2+4x+4=0\)
- \(8x^2+14x+3=0\)
- \(3x^2−5x−2=0\)
- \(3x^2−10x+15=0\)
Рішення
Обчисліть дискримінант\(b^2−4ac\) для кожного рівняння і вкажіть очікуваний тип розв'язків.
а.
\(x^2+4x+4=0\)
\(b^2-4ac={(4)}^2-4(1)(4)=0\)Буде одне раціональне подвійне рішення.
б.
\(8x^2+14x+3=0\)
\(b^2-4ac={(14)}^2-4(8)(3)=100\)Як і\(100\) ідеальний квадрат, буде два раціональних рішення.
c.
\(3x^2−5x−2=0\)
\(b^2-4ac={(-5)}^2-4(3)(-2)=49\)Як і\(49\) ідеальний квадрат, буде два раціональних рішення.
д.
\(3x^2−10x+15=0\)
\(b^2-4ac={(-10)}^2-4(3)(15)=-80\)Буде два складних рішення.
Використання теореми Піфагора
Однією з найвідоміших формул в математиці є теорема Піфагора. Він заснований на прямокутному трикутнику, і стверджує співвідношення між довжинами сторін як\(a^2+b^2=c^2\), де\(a\) і\(b\) відносяться до катетів прямокутного трикутника, прилеглого до\(90°\) кута, і\(c\) відноситься до гіпотенузи. Він має безмірне використання в архітектурі, інженерії, науках, геометрії, тригонометрії та алгебрі, а також у повсякденних додатках.
Ми використовуємо теорему Піфагора для розв'язання довжини однієї сторони трикутника, коли ми маємо довжини двох інших. Оскільки кожен з членів знаходиться в квадраті в теоремі, коли ми вирішуємо для сторони трикутника, ми маємо квадратне рівняння. Ми можемо використовувати методи розв'язання квадратичних рівнянь, які ми дізналися в цьому розділі, для вирішення для відсутньої сторони.
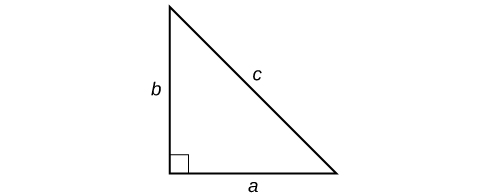
Теорема Піфагора дається як
\[a^2+b^2=c^2\]
де\(a\) і\(b\) відносяться до катетів прямокутного трикутника, прилеглого до\(90°\) кута, і\(c\) відноситься до гіпотенузи, як показано в.
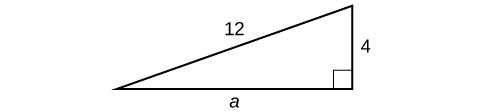
Знайдіть довжину відсутньої сторони прямокутного трикутника на малюнку\(\PageIndex{5}\).
Рішення
Оскільки у нас є вимірювання для сторони\(b\) та гіпотенузи, відсутня сторона є\(a\).
\[\begin{align*} a^2+b^2&= c^2\\ a^2+{(4)}^2&= {(12)}^2\\ a^2+16&= 144\\ a^2&= 128\\ a&= \sqrt{128}\\ &= 8\sqrt{2} \end{align*}\]
Використовуйте теорему Піфагора для вирішення проблеми прямокутного трикутника: Leg a вимірює 4 одиниці, нога b вимірює 3 одиниці. Знайти довжину гіпотенузи.
- Відповідь
-
\(5\)одиниць
Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з квадратними рівняннями.
- Розв'язування квадратних рівнянь методом факторингу
- Властивість нульового продукту
- Завершення площі
- Квадратична формула з двома раціональними розв'язками
- Довжина ніжки прямокутного трикутника
Ключові рівняння
| квадратична формула | \(x=\dfrac{−b±\sqrt{b^2-4ac}}{2a}\) |
Ключові концепції
- Багато квадратні рівняння можуть бути вирішені факторингом, коли рівняння має провідний коефіцієнт\(1\) або якщо рівняння є різницею квадратів. Потім властивість нульового фактора використовується для пошуку рішень. Див. розділ Приклад, Приклад та Приклад.
- Багато квадратні рівняння з провідним коефіцієнтом, відмінним від,\(1\) можуть бути вирішені факторингом за допомогою методу групування. Див. Приклад і Приклад.
- Ще одним методом розв'язання квадратики є властивість квадратного кореня. Змінна знаходиться в квадраті. Виділяємо квадратний член і беремо квадратний корінь обох сторін рівняння. Рішення дасть позитивне і негативне рішення. Див. Приклад і Приклад.
- Завершення квадрата є методом розв'язання квадратних рівнянь, коли рівняння неможливо врахувати. Див. Приклад.
- Високо надійним методом розв'язання квадратних рівнянь є квадратична формула, заснована на коефіцієнтах і постійному члені в рівнянні. Див. Приклад.
- Дискримінант використовується для позначення природи коренів, які дасть квадратне рівняння: реальне або складне, раціональне чи ірраціональне, і скільки з них. Див. Приклад.
- Теорема Піфагора, одна з найвідоміших теорем в історії, використовується для вирішення задач прямокутного трикутника і має застосування в численних областях. Розв'язування довжини однієї сторони прямокутного трикутника вимагає розв'язання квадратного рівняння. Див. Приклад.
