4.8: Зворотні функції

Last updated
Save as PDF

Page ID: 58798

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Обернена функція скасовує дію початкової функції. Таким чином, зворотна функція, яка в квадраті число буде функція, яка квадрат вкорінені число. Загалом, обернена функція буде приймати$y$ значення з початкової функції і повертати$x$ значення, яке її спричинило.

Ми можемо побачити це в додатку. Враховуючи об'єкт з невеликим або відсутнім опором повітря$100 \mathrm{ft}$, з якого скидається, функція, яка описує його висоту як функцію часу, буде такою:
\ [
H (t) =100-16 t^ {2}
\]
У цій функції$H(t)$ є висотою об'єкта в часі $t .$Якби ми хотіли, щоб повернути це навколо так, що він описав час для заданої висоти, то ми хотіли б ізолювати$t$ змінну. У цьому прикладі графік функції зміниться в тому, що вихідна незалежна змінна -$t,$ стає залежною змінною в оберненій функції.
\ [
\ почати {вирівняний}
h &=100-16 t^ {2}\\ 16 t^ {2} &=100-год\\ t^ {2} &=\ розрив {100-h} {
16}\
t &=\ sqrt {\ frac {100-h} {16}}\ T (h) &=\ розрив {\
sqrt {100-h}} {4}\ T (h) &=\ розрив {\ sqrt {100-h}} {4}\
T (h) &=\ розрив {\ sqrt {100-h}} {4}
\ T (h) &=\ розрив вирівняні}
\]

Оригінальна функція:$H(t)=100-16 t^{2}$
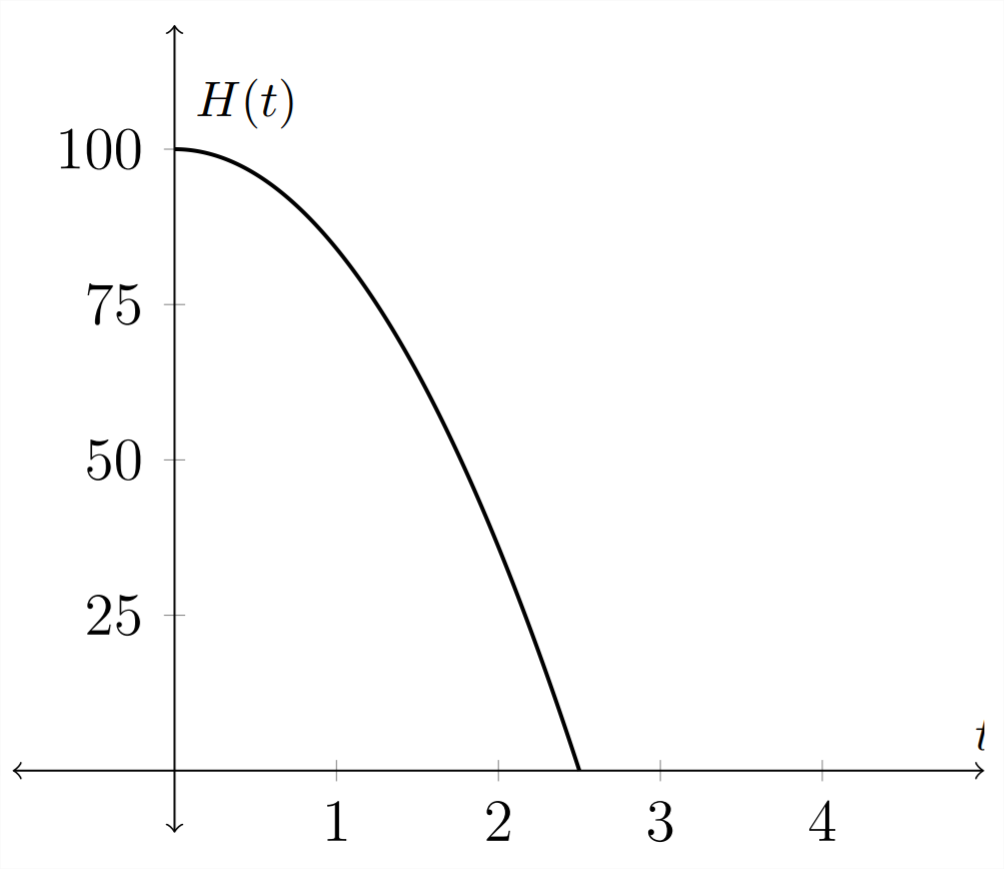
$clipboard_e3860268f9d6975d40696f81c10a4e402.png$
Зворотна функція:$T(h)=\frac{\sqrt{100-h}}{4}$
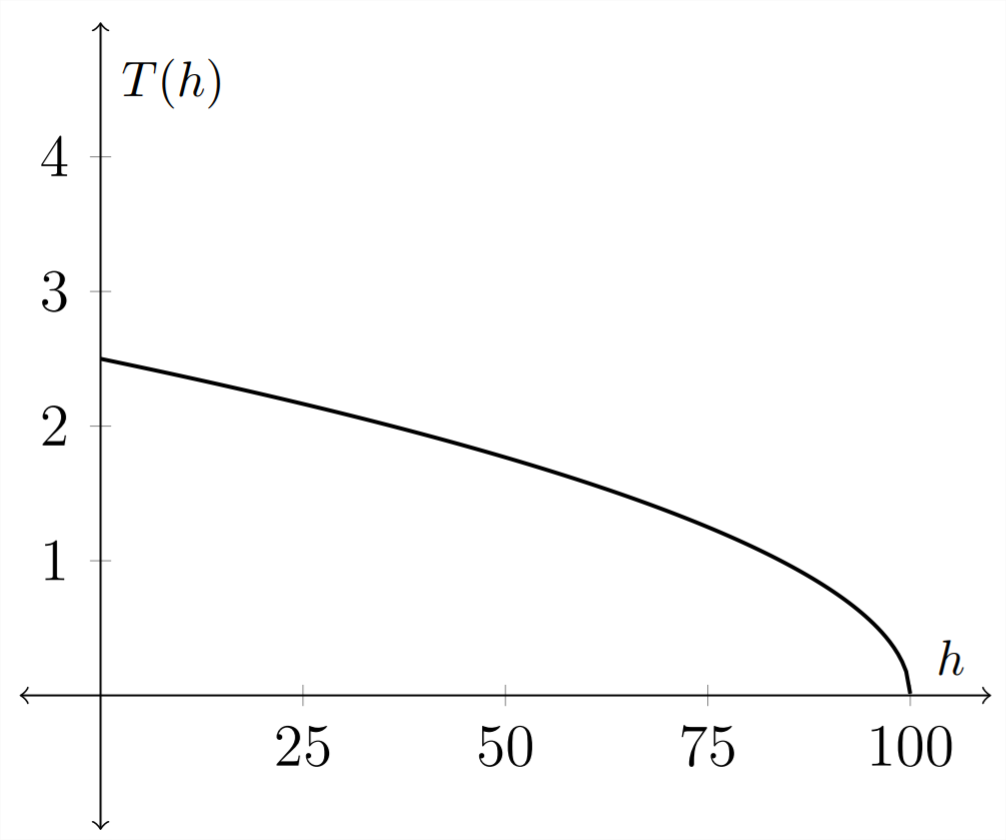
$clipboard_e89256480f8675d2b57ce0801450f241e.png$
Зверніть увагу, що графік функції, оберненої, є вихідною функцією, відображеною над лінією,$y=x,$ оскільки обернена функція змінює незалежну та залежні змінні.

Пошук формули для оберненої функції може бути більш заплутаним, якщо розглядати стандартну функцію.$y=f(x) .$ У нашому стандартному позначенні завжди$x$ вважається незалежною змінною і завжди$y$ вважається залежною змінною.

Зверніть увагу в прикладі вище, що коли ми графікували функцію та її зворотний, мітка на$x$ осі змінилася з$t$ на$h .$ У стандартній функції$x$ вісь завжди буде$x$ віссю, а$y$ вісь завжди буде$y$ віссю. Щоб компенсувати це, коли ми знаходимо функцію, обернену для функції, зазначеної з точки зору,$x$ і$y$ ми, як правило, обмінюємося$x$ і$y$ термінами так, що$x$ залишається незалежною змінною.
У нашому прикладі ми мали
\ [
H (t) =100-16 t^ {2}
\]
і знайшли зворотне значення
\ [
T (h) =\ frac {\ sqrt {100-h}} {4}
\]
Якщо вихідна функція була заявлена в терміні $x$і$y,$ тоді процес виглядав би так:
\ begin {вирівняний}
f (x) &=100-16 x^ {2}\\
y &=100-16 x^ {2}\\
16 x^ {2} &=100-y\\
x^ {2} &=\ frac {100-y} {16}\
x &=\ sqrt {\ frac {100-y} {16}}\
x &=\ frac {\ sqrt {100-y}} {4}
\ end {вирівняний}

Потім ми перемикаємо$y$ змінні$x$ і, щоб зберегти$x$ як незалежну змінну:
\ [
y=f^ {-1} (x) =\ frac {\ sqrt {100-x}} {4}
\]
$\mathrm{So}$
\ [
f (x) =100-16 x^ {2}
\]
і
\ [
f^ {-1} (x) =\ розрив {\ sqrt {100-x}} {4}
\]

Вправи 4.8
З$f(x),$ заданою функцією знайдіть обернену функцію$f^{-1}(x)$
1)$\quad f(x)=3 x$
2)$\quad f(x)=-4 x$
3)$\quad f(x)=4 x+2$
4)$\quad f(x)=1-3 x$
5)$\quad f(x)=x^{3}-1$
6)$\quad f(x)=x^{3}+1$
7)$\quad f(x)=x^{2}+4 (x \geq 4)$
8)$\quad f(x)=x^{2}+9 (x \geq 9)$
9)$\quad f(x)=\frac{4}{x}$
10)$\quad f(x)=-\frac{3}{x}$
11)$\quad f(x)=\frac{1}{x-2}$
12)$\quad f(x)=\frac{4}{x+2}$
13)$\quad f(x)=\frac{2}{x+3}$
14)$\quad f(x)=\frac{4}{2-x}$
15)$\quad f(x)=\frac{3 x}{x+2}$
16) $\quad f(x)=-\frac{2 x}{x-1}$
17)$\quad f(x)=\frac{2 x}{3 x-1}$
18)$\quad f(x)=-\frac{3 x+1}{x}$
19)$\quad f(x)=\frac{3 x+4}{2 x-3}$
20)$\quad f(x)=\frac{2 x-3}{x+4}$
21)$\quad f(x)=\frac{2 x+3}{x+2}$
22)$\quad f(x)=-\frac{3 x+4}{x-2}$
Знайдіть обернену функцію для кожного з наступних додатків.
23) Обсяг води, що залишився в резервуарі на 1000 галонів, який стікає за 40 хвилин, моделюється рівнянням:
\ [
V (t) =1000\ left (1-\ frac {t} {40}\ праворуч) ^ {2}
\]
Find$T(v)$ - функція, яка повідомляє, як довго була вода зливу з огляду на той чи інший обсяг, що залишився в баку. Час вимірюється в хвилинах, а обсяг вимірюється в галонів.
24) Швидкість транспортного засобу в милі на годину, що залишає сліди ковзання довжиною$d$ ноги, моделюється рівнянням:
\ [
R (d) =2\ sqrt {5 d}
\]
Find$D(r)$ - функція, яка повідомляє вам гальмівний шлях для транспортного засобу проїзні$r$ милі на годину.
25) Період маятника довжини$\ell$ може бути виражений співвідношенням:
\ [
T (\ ell) =2\ pi\ sqrt {\ frac {\ ell} {980}}
\]
Знайти функцію$L(t)$, яка визначає довжину маятника з урахуванням його періоду. Тут час вимірюється в секундах, а довжина вимірюється в сантиметрах.
26) Обсяг сфери радіуса$r$ задається формулою:
\ [
V (r) =\ frac {4} {3}\ pi r^ {3}
\]
Find$R(v)$ - функція, яка визначає радіус сфери з огляду на її об'єм.