1.4: Комплексні числа

Last updated
Save as PDF

Page ID: 58856

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Нашу систему числення можна поділити різними способами. Найосновнішою формою математики є підрахунок, і майже всі людські культури мають слова для представлення чисел (Піраха Південної Америки є помітним винятком). Таким чином, найосновнішим набором чисел є набір лічильних чисел, представлених подвійною забороною$\mathrm{N}: \mathbb{N}=\{1,2,3,4,5,6,7, \ldots\}$ (ми відкладемо дискусію щодо того, чи слід включати нуль до цього набору).

Якщо ми спробуємо відняти більшу кількість підрахунку з меншого числа підрахунку, ми виявимо, що в наборі рахункових чисел немає членів, які представляють відповідь у цій ситуації. Це розширює набір натуральних чисел до безлічі цілих чисел:$\mathbb{Z}=\{\ldots,-3,-2,-1,0,1,2,3, \ldots\} .$ Цілі числа представлені подвійною смугою$Z$, для німецького слова для чисел - «zahlen». У самих ранніх появах негативних чисел у китайських та індійських математичних системах негативні значення часто використовувались для представлення боргу. Оскільки грецька математика ґрунтувалася на геометрії, вони не використовували негативних чисел.

Переходячи до множення та ділення, якщо ми ставимо під сумнів значення$8 \div 2=4$ проти,$8 \div 3=?,$ ми знову повинні розширити нашу концепцію чисел, щоб дати відповідь на друге питання$8 \div 3=?$. Розуміння співвідношень цілих чисел або раціональних чисел дозволяє розв'язати такі задачі. Множина раціональних чисел представлена подвійною$Q$ смугою, щоб представляти частку:
$\mathbb{Q}=\left\{\frac{a}{b}: a, b \in \mathbb{Z}\right\}$

Грецьке розуміння чисел в основному зупинилося на цьому. Вони вважали, що всі величини можуть бути представлені у вигляді співвідношення цілих чисел. Довжина діагоналі квадрата, сторони якого мають довжину 1, викликала значний жах у піфагорійців в результаті цього. Використання теореми Піфагора для діагоналі квадрата, сторони якого мають довжину 1, показує, що діагональ буде$c^{2}=1^{2}+1^{2}=2,$ таким чином$c=\sqrt{2} .$ Це число не може бути представлено у вигляді співвідношення цілих чисел. Цей новий клас чисел додає набір
ірраціональних чисел до існуючого набору раціональних чисел для створення Реальних чисел, представлених подвійною смугою$\mathrm{R}$:$\mathbb{R}$.

Ця ієрархія чисел часто представлена на наступній схемі:
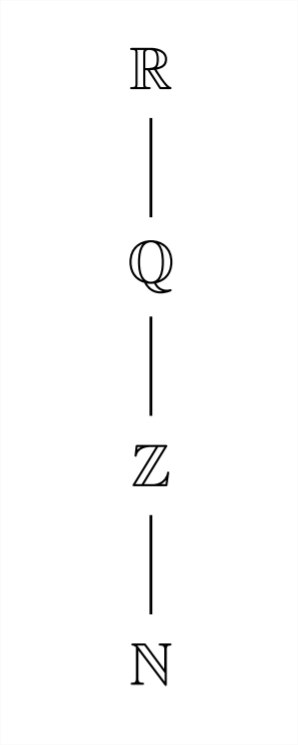
$clipboard_e993bb2370ae519520abd9c2f425f04ea.png$

Один з найкращих способів концептуалізації Реального числа знаходиться на числовій лінії - кожна точка на числовій лінії відповідає унікальному Реальному числу, а кожне Реальне число відповідає унікальній позиції на рядку Реального числа.

$clipboard_ebc7d56f632ad20515407a4ba729c32e6.png$

Після розвитку друкарського верстата в 15 столітті Лібер Абачі Фібоначчі перевели на італійську мову з латини і читали по всій Італії. В результаті Італія стала процвітаючим центром математики аж до 17-го століття, коли центр європейської математики перемістився на північ до Франції, Німеччини та Англії.

Протягом 1500-х років італійські математики, такі як Джироламо Кардано, Рафаель Бомбеллі та Нікколо Фонтана Тарталья працювали над розширенням ідей у книзі Фібоначчі. Вони створили формули для розв'язання кубічних ($x^{3}$) та квартичних ($x^{4}$) рівнянь ступеня. При вирішенні деяких з цих рівнянь вони виявили, що їх формули іноді виробляють від'ємні значення під квадратним коренем. Жодна з відомих систем числення не могла вмістити цю можливість. У книзі Кардано про алгебру Ars Magna він стикається з проблемою, яка включає квадратний корінь від'ємного числа. Він каже: «Зрозуміло, що цей випадок неможливий. Проте ми працюватимемо таким чином...» і він приступає до обчислення дійсного комплексного рішення проблеми. Математики врешті-решт визначили складну одиницю,$\sqrt{-1}=i$ а потім

розробили систему, в якій всі комплексні числа являють собою комбінацію дійсної частини
$(a)$ і «уявної» частини (бі).
Комплексні числа - це двовимірна система числення, представлена подвійною смугою,$C: \mathbb{C}=\{a+b i: a, b \in \mathbb{R}\},$ де$i$ є комплексна одиниця, визначена як$i=\sqrt{-1} .$ Протягом кінця 1700-х і початку 1800-х математики поступово рухалися до геометричної інтерпретації двовимірного комплексні числа. Те, що сьогодні відомо як «діаграма Арганда» являє собою реальну цінну частину комплексного числа вздовж горизонтальної осі та кратну комплексної одиниці вздовж вертикальної осі.

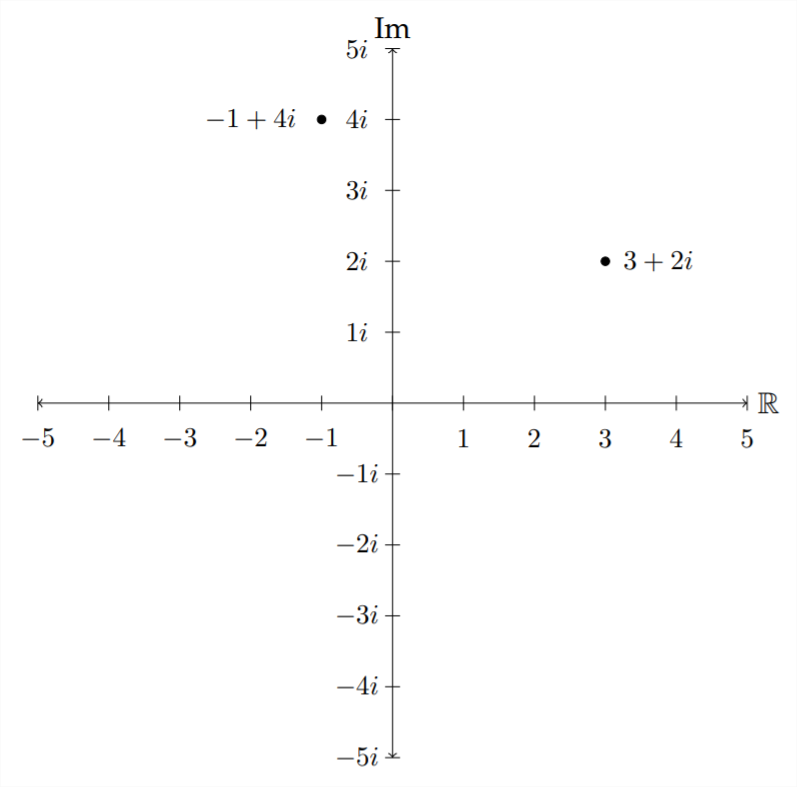
$clipboard_e7bfee771d9948acf99c81e56e14863a8.png$

Висловлення квадратних коренів негативних чисел

Квадратні корені від'ємних величин, як правило, виражаються кратними$i$

Приклад$\PageIndex{1}$

\ [
\ почати {масив} {c}
\ sqrt {-4} =2 я\\
\ sqrt {-25} =5 я\\
\ sqrt {-7}\ приблизно 2.646 я
\ кінець {масив}
\]

Додавання, віднімання та множення комплексними числами

Обчислення комплексними числами має багато схожості з роботою зі змінними. Реальна частина і уявна частина розглядаються окремо для додавання і віднімання, але можуть бути перемножені і розділені.

Приклад$\PageIndex{2}$

Обчисліть наступне:

\ [
\ почати {масив} {c}
(6-4 i) + (-2+7 i) =4+3 i\\
(-9+2 i) - (-4+6 i) =-9+2 i+4-6 i=-5-4 i\\
3 (10+i) =30+3 i\\
-7 i (-5+8 i) =35 i-56 i ^ {2}
\ кінець {масив}
]

Тепер ми стикаємося з цікавим фактом про комплексних числах і, зокрема, комплексної одиниці за$i .$ визначенням,$i=\sqrt{-1} .$ Тому, якщо$i$ ми квадрат ми повинні отримати$-1 .$ В останньому прикладі завдання вище, ми можемо$i^{2}$ замінити на -1, щоб закінчити задачу.

\ почати {вирівняний}
-7 i (-5+8 i) &=35 i-56 i ^ {2}\
&= 35 i-56 (-1)\\
&= 35 i+56\\
&=56+35 i
\ кінець {вирівняний}

Приклад$\PageIndex{3}$

Обчисліть наступне:

\ [
\ почати {вирівняний}
(8-5 я) (1-4 я) &=8-32 i-5 i+20 i^ {2}\
&=8-37 i+20 (-1)\\
&=8-37 i-20\\
&=-12-37 i
\\\\
(9+2 i) ^ {2} & =( 9+2 i) (9+2 я)\\
=81+18 i+4 i^ {2}\\
&=81+36 i+4 (-1)\\
&=81+36 i-4\\
&=77+36 i
\ кінець {вирівняний}
\]

повноваження$i$

Сили$i$ слідувати цікавою схемою, заснованої на визначенні, що$i^{2}=-1$
Ми можемо бачити, що$i^{1}=i$ і що$i^{3}=i^{2} * i^{1}=-1 * i=-i$
в$i^{2}=-1,$ результаті, Аналогічним чином,$i^{4}=i^{2} * i^{2}=(-1)(-1)=1$
Це означає, що$i^{5}=i^{4} * i=1 * i=i$
Якщо ми поставимо все цю інформацію разом ми отримуємо наступне:
$i^{1}=i$
$i^{2}=-1$
$i^{3}=-i$
$i^{4}=1$
$i^{5}=i^{1}=i$
$i^{6}=i^{2}=-1$
$i^{7}=i^{3}=-i$
$i^{8}=i^{4}=1$
Іншими словами, кожна сила$i$ еквівалентна$i,-1,-i,$ або або$1 .$ Щоб визначити, яке з цих значень$i$ є рівнозначною, нам потрібно знайти залишок показника, коли він ділиться на 4

Приклад$\PageIndex{4}$

Спростити$i^{38}$

Рішення

так як кожен$i^{38}=i^{36} * i^{2}=\left(i^{4}\right)^{9} * i^{2}=1^{9} * i^{2}=i^{2}=-1$
з тих$i^{4}=1,$ пір 38 є 2 більше, ніж кратне$4,$ тоді$i^{38}=i^{2}=-1$

Вправа$\PageIndex{1}$

$clipboard_eb2540db434772022cb74d540cb2aca43.png$
Графік наведено наступні комплексні числа:

1)$\quad 2+5 i$
2)$\quad 4-3 i$
3)$\quad -2+6 i$
4)$\quad -3-5 i$
5)$\quad 4$
6)$\quad -2 i$
7)$\quad 7-i$
8)$\quad -1+i$
9)$\quad -8+4 i$
10)$\quad 8+3 i$
11) $\quad 7 i$
12)$\quad -5-9 i$

Висловіть кожну величину через ірраціональні значення$i .$ Round до найближчих 1000 го.
13)$\quad \sqrt{-36}$
14)$\quad \sqrt{-81}$
15)$\quad \sqrt{-100}$
16)$\quad \sqrt{-49}$
17)$\quad \sqrt{-4}$
18)$\quad \sqrt{-25}$
19)$\quad \sqrt{-2}$
20)$\quad \sqrt{-6}$
21)$\quad \sqrt{-10}$
22) $\quad \sqrt{-31}$
23)$\quad \sqrt{-5}$
24)$\quad \sqrt{-3}$

Виконати зазначену операцію і спростити
25)$\quad(6+7 i)+(5+3 i)$
26)$\quad(4-5 i)+(3+9 i)$
27)$\quad(9+8 i)-(1-2 i)$
28)$\quad(2+i)-(6-4 i)$
29)$\quad(7-4 i)-(5-3 i)$
30)$\quad(8+i)-(4+3 i)$
31)$\quad(7 i)(6 i)$
32)$\quad(4 i)(-8 i)$
33)$\quad(-2 i)(5 i)$
34)$\quad(12 i)(3 i)$
35)$\quad(1+i)(3+2 i)$
36)$\quad(1+5 i)(4+3 i)$
37)$\quad(6-5 i)(2-3 i)$
38)$\quad(8-3 i)(2+i)$
39)$\quad(-3+4 i)(-1-2 i)$
40)$\quad(-7-i)(3-5 i)$
41)$\quad(4-2 i)^{2}$
42) $\quad(-5+i)^{2}$
43)$\quad(3+i)(3-i)$
44)$\quad(2+6 i)(2-6 i)$
45)$\quad(9-4 i)(9+4 i)$
46)$\quad(5+2 i)(5-2 i)$

Експрес як$i,-1,-i,$ або 1
47)$\quad i^{3}$
48)$\quad i^{7}$
49)$\quad i^{21}$
50)$\quad i^{13}$
51)$\quad i^{29}$
52)$\quad i^{56}$
53)$\quad i^{72}$
54)$\quad i^{35}$
55) $\quad i^{66}$
56)$\quad i^{103}$
57)$\quad i^{16}$
58)$\quad i^{53}$
59)$\quad i^{11}$
60)$\quad i^{42}$
61)$\quad i^{70}$
62)$\quad i^{9}$

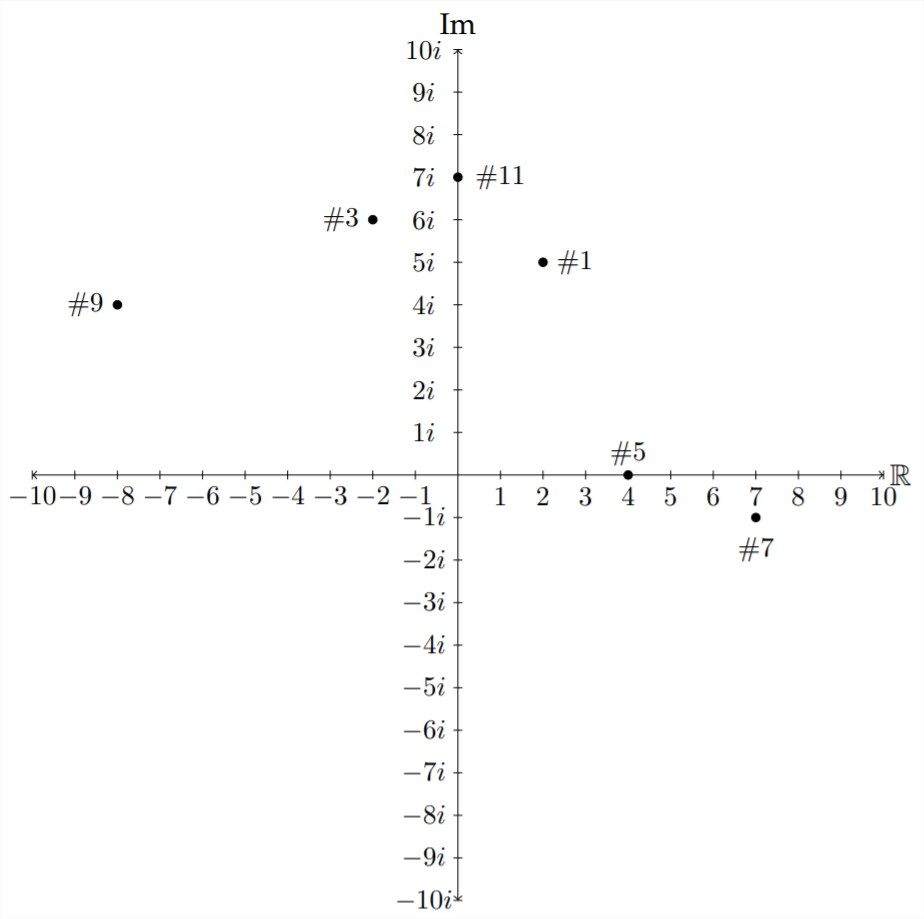
Відповідь: $clipboard_e18ab098a4753b9b24714874b6ca27943.png$
13)$\quad 6 i$
15)$\quad 10 i$
17)$\quad 2 i$
19)$\quad 1.414 i$
21)$\quad 3.162 i$
23)$\quad 2.236 i$
25)$\quad 11+10 i$
27)$\quad 8+10 i$
29)$\quad 2-i$
31)$\quad-42$
33)$\quad 10$
35)$\quad 1+5 i$
37)$\quad-3-28 i$
39)$\quad 11+2 i$
41)$\quad 12-16 i$
43)$\quad 10$
45) $\quad 97$
47)$\quad -i$
49)$\quad i$
51)$\quad i$
53)$\quad 1$
55)$\quad -1$
57)$\quad 1$
59)$\quad -i$
61)$\quad -1$