3.2: Функції та позначення функцій

Визначення того, чи відповідає зв'язок функцію

Відношення - це набір впорядкованих пар. Набір перших компонентів кожної впорядкованої пари називається доменом, а набір других компонентів кожної впорядкованої пари називається діапазоном. Розглянемо наступний набір впорядкованих пар. Перші числа в кожній парі - це перші п'ять натуральних чисел. Друге число в кожній парі вдвічі більше першого.

\[\{(1, 2), (2, 4), (3, 6), (4, 8), (5, 10)\}\tag{1.1.1}\]

Домен є$\{1, 2, 3, 4, 5\}$. Асортимент є$\{2, 4, 6, 8, 10\}$.

Зверніть увагу, що кожне значення в домені також відоме як вхідне значення або незалежна змінна і часто позначається малою літерою$x$. Кожне значення в діапазоні також відоме як вихідне значення або залежна змінна, і часто позначається малою літерою$y$.

Функція$f$ - це відношення, яке присвоює кожному значенню в області одне значення в діапазоні. Іншими словами, no$x$ -значення повторюються. Для нашого прикладу, який пов'язує перші п'ять натуральних чисел з числами, подвоюють їх значення, це відношення є функцією, оскільки кожен елемент в області, {1, 2, 3, 4, 5}, парний рівно з одним елементом в діапазоні,$\{2, 4, 6, 8, 10\}$.

Тепер розглянемо набір впорядкованих пар, що пов'язує терміни «парне» і «непарне» з першими п'ятьма натуральними числами. Це виглядало б як

\[\mathrm{\{(odd, 1), (even, 2), (odd, 3), (even, 4), (odd, 5)\}} \tag{1.1.2}\]

Зверніть увагу, що кожен елемент у домені, {парний, непарний} не парний з точно одним елементом в діапазоні,$\{1, 2, 3, 4, 5\}$. Наприклад, термін «непарний» відповідає трьом значенням з діапазону,$\{1, 3, 5\},$ а термін «парний» відповідає двом значенням з діапазону,$\{2, 4\}$. Це порушує визначення функції, тому це відношення не є функцією.

Рисунок$\PageIndex{1}$ порівнює відносини, які є функціями, а не функціями.

[Три відносини, які демонструють, що складають функцію.] — Рисунок$\PageIndex{1}$: (a) Цей зв'язок є функцією, оскільки кожен вхід пов'язаний з одним виходом. Зверніть увагу, що вхід$q$ і$r$ обидва дають вихід$n$. (б) Цей зв'язок також є функцією. При цьому кожен вхід пов'язаний з одним виходом. (c) Цей зв'язок не є функцією, оскільки вхід$q$ пов'язаний з двома різними виходами.

Функція

Функція - це відношення, в якому кожне можливе вхідне значення призводить до рівно одного вихідного значення. Ми говоримо «вихід - це функція входу».

Вхідні значення складають домен, а вихідні значення складають діапазон.

Як: Враховуючи зв'язок між двома величинами, визначте, чи є зв'язок функцією

Визначте вхідні значення.
Визначте вихідні значення.
Якщо кожне вхідне значення призводить лише до одного вихідного значення, класифікуйте зв'язок як функцію. Якщо будь-яке вхідне значення призводить до двох або більше виходів, не класифікуйте зв'язок як функцію.

Приклад$\PageIndex{1}$: Determining If Menu Price Lists Are Functions

Меню кав'ярні, представлене на малюнку,$\PageIndex{2}$ складається з позицій і їх цін.

Чи є ціна функцією елемента?
Чи є товар функцією ціни?

Меню пончиків ціни з кав'ярні, де звичайний пончик становить $1,49, а желе пончик і шоколадний пончик - $1,99. — Малюнок$\PageIndex{2}$: Меню пончиків цін з кав'ярні, де звичайний пончик становить $1.49, а желе пончик і шоколадний пончик - $1.99.

Рішення

Почнемо з розгляду введення як пунктів меню. Вихідні значення - це ціни. Див$\PageIndex{3}$. Малюнок.

Кожен пункт меню має тільки одну ціну, тому ціна є функцією елемента.

Два пункти меню мають однакову ціну. Якщо ми розглядаємо ціни як вхідні значення, а елементи - виходом, то одне і те ж вхідне значення може мати більше одного виходу, пов'язаного з ним. Див$\PageIndex{4}$. Малюнок.

[Асоціація цін на пончики.] — Малюнок$\PageIndex{4}$: Асоціація цін на пончики.

Тому товар не є функцією ціни.

Приклад$\PageIndex{2}$: Determining If Class Grade Rules Are Functions

У конкретному класі математики загальний відсоток балів відповідає середньому балу. Чи середній бал класу є функцією відсотка класу? Чи є відсотковий клас функцією середнього балу? $\PageIndex{1}$У таблиці наведено можливе правило для присвоєння балів балів.

Таблиця$\PageIndex{1}$: Класні бали.
Відсоток класу	0—56	57—61	62-66	67—71	72—77	78—86	87—91	92—100
Середній бал	0.0	1.0	1.5	2.0	2.5	3.0	3.5	4.0

Рішення

Для будь-якого відсотка заробленого класу існує асоційований середній бал, тому середня оцінка балів є функцією відсотка класу. Іншими словами, якщо ми введемо відсоток класу, виходом буде конкретний середній бал.

У наведеній системі оцінювання існує діапазон процентних оцінок, які відповідають одному і тому ж середньому балу. Наприклад, студенти, які отримують середній бал 3,0, можуть мати різні відсотки оцінок, починаючи від 78 до 86. Таким чином, відсоток класу не є функцією середнього балу.

Вправа$\PageIndex{2}$

У таблиці$\PageIndex{2}$ перераховані п'ять найбільших бейсболістів всіх часів в порядку рангу.

Таблиця$\PageIndex{2}$: П'ять найбільших бейсболістів.
Гравець	Ранг
немовля Рут	1
Віллі Мейс	2
Тай Кобб	3
Уолтер Джонсон	4
Хенк Аарон	5

Чи є ранг функцією імені гравця?
Чи є ім'я гравця функцією рангу?

Відповідь на: Так
Відповідь б: так. (Примітка: Якби два гравці були прив'язані до, скажімо, 4-го місця, то ім'я не було б функцією рангу.)

Використання позначення функцій

Після того, як ми визначимо, що зв'язок є функцією, нам потрібно відобразити та визначити функціональні відносини, щоб ми могли їх зрозуміти та використовувати, а іноді і так, щоб ми могли запрограмувати їх у комп'ютери. Існують різні способи представлення функцій. Стандартне позначення функції - це одне представлення, яке полегшує роботу з функціями.

Щоб представити «висота - це функція віку», ми починаємо з визначення описових змінних$h$ для висоти та$a$ віку. Букви$f$$g$, і часто$h$ використовуються для представлення функцій так само, як ми використовуємо$x$$y$, і$z$ для представлення чисел і$A$$B$, і$C$ для представлення множин.

\[\begin{array}{ll} h \text{ is } f \text{ of }a \;\;\;\;\;\; & \text{We name the function }f \text{; height is a function of age.} \\ h=f(a) & \text{We use parentheses to indicate the function input.} \\ f(a) & \text{We name the function }f \text{ ; the expression is read as “ }f \text{ of }a \text{.”}\end{array}\]

Пам'ятайте, що ми можемо використовувати будь-яку букву, щоб назвати функцію; позначення$h(a)$ показує нам, що$h$ залежить від$a$. Значення$a$ необхідно поставити в функцію,$h$ щоб отримати результат. Дужки вказують на те, що у функцію вводиться вік; вони не вказують на множення.

Ми також можемо дати алгебраїчний вираз як вхідні дані функції. Наприклад,$f(a+b)$ означає «спочатку додати$a$ і$b$, а результат - вхід для функції$f$.» Операції необхідно виконувати в такому порядку, щоб отримати правильний результат.

Функція позначення

Позначення$y=f(x)$ визначає функцію з іменем$f$. Це читається як «$y$є функцією»$x$. Буква$x$ представляє вхідне значення, або незалежну змінну. Буква$y$, або$f(x)$, представляє вихідне значення, або залежну змінну.

Приклад$\PageIndex{3}$: Using Function Notation for Days in a Month

Використовуйте позначення функції для представлення функції, чиї вхідні дані - ім'я місяця, а вивід - кількість днів у цьому місяці.

Рішення

Використання позначення функцій для днів у місяці

Використовуйте позначення функції для представлення функції, чиї вхідні дані - ім'я місяця, а вивід - кількість днів у цьому місяці.

Кількість днів у місяці є функцією імені місяця, тому якщо ми називаємо функцію$f$, ми пишемо$\text{days}=f(\text{month})$ або$d=f(m)$. Назва місяця - це вхід до «правила», яке пов'язує певне число (вихід) з кожним входом.

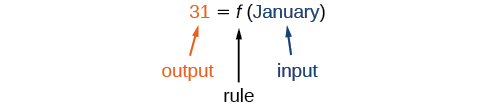
Функція 31 = f (січень), де 31 - вихід, f - правило, а січень - вхід. — Малюнок$\PageIndex{5}$: Функція,$31 = f(January)$ де 31 - вихід, f - правило, а січень - вхід.

Наприклад$f(\text{March})=31$, тому що березень має 31 день. Позначення$d=f(m)$ нагадує нам, що кількість днів,$d$ (вихідних), залежить від назви місяця,$m$ (вхідного).

Аналіз

Зауважте, що входами функції не обов'язково повинні бути числами; входами функції можуть бути імена людей, мітки геометричних об'єктів або будь-який інший елемент, який визначає якийсь вихід. Однак більшість функцій, з якими ми будемо працювати в цій книзі, матимуть числа як входи, так і виходи.

Приклад$\PageIndex{3B}$: Interpreting Function Notation

Функція$N=f(y)$ дає кількість поліцейських$N$, у місті на рік$y$. Що$f(2005)=300$ являє собою?

Рішення

Коли ми читаємо$f(2005)=300$, ми бачимо, що рік введення - 2005. Значення на виході, чисельність співробітників поліції$(N)$, становить 300. Пам'ятайте,$N=f(y)$. У$f(2005)=300$ заяві йдеться про те, що в 2005 році в місті було 300 поліцейських.

Вправа$\PageIndex{3}$

Використовуйте позначення функції, щоб висловити вагу свині в фунтах в залежності від її віку в днях$d$.

Відповідь: $w=f(d)$

Q&A

Замість позначення$y=f(x)$, наприклад, ми могли б використовувати той самий символ для виведення, що і для функції, наприклад$y=y(x)$, означає «$y$є функцією$x$?»

Так, це часто робиться, особливо в прикладних предметах, які використовують вищу математику, такі як фізика та інженерія. Однак, вивчаючи саму математику, ми любимо підтримувати відмінність між функцією$f$, такою як правило або процедура, і вихід y, який ми отримуємо, застосовуючи$f$ до певного входу$x$. Ось чому ми зазвичай використовуємо позначення, такі як$y=f(x),P=W(d)$, і так далі.

Представлення функцій за допомогою таблиць

Поширеним методом представлення функцій є у вигляді таблиці. У рядках або стовпцях таблиці відображаються відповідні вхідні та вихідні значення. У деяких випадках ці значення представляють все, що ми знаємо про відносини; в інших випадках таблиця містить кілька прикладів вибору з більш повних відносин.

У таблиці$\PageIndex{3}$ наведено вхідне число кожного місяця ($\text{January}=1$$\text{February}=2$, тощо) та вихідне значення кількості днів у цьому місяці. Ця інформація представляє все, що ми знаємо про місяці та дні для даного року (тобто не високосний рік). Зауважте, що в цій таблиці ми визначаємо функцію «дні в місяці»,$f$ де$D=f(m)$ визначають місяці цілим числом, а не за іменем.

Таблиця$\PageIndex{3}$: Місяці і кількість днів на місяць.
Номер місяця,$m$ (вхід)	1	2	3	4	5	6	7	8	9	10	11	12
Днів у місяці,$D$ (вихідний)	31	28	31	30	31	30	31	31	30	31	30	31

Таблиця$\PageIndex{4}$ визначає функцію$Q=g(n)$ Remember, це позначення говорить нам, що$g$ це ім'я функції, яка приймає вхід$n$ і дає вихід$Q$.

Таблиця$\PageIndex{4}$: Функція$Q=g(n)$
$n$	1	2	3	4	5
$Q$	8	6	7	6	8

Таблиця$\PageIndex{5}$ відображає вік дітей в роках і відповідні їм висоти. У цій таблиці відображаються лише деякі дані, доступні для зросту та віку дітей. Ми відразу бачимо, що ця таблиця не представляє функцію, тому що одне і те ж вхідне значення, 5 років, має два різних вихідних значення, 40 дюйм. і 42 дюйма.

Таблиця$\PageIndex{5}$: Вік дітей і відповідні їм зростання.
Вік в роках,$a$ (вхід)	5	5	6	7	8	9	10
Висота в дюймах,$h$ (вихід)	40	42	44	47	50	52	54

Як: За допомогою таблиці вхідних та вихідних значень визначте, чи є таблиця функцією

Визначте вхідні та вихідні значення.
Перевірте, чи кожне вхідне значення поєднується лише з одним вихідним значенням. Якщо так, то таблиця представляє функцію.

Приклад$\PageIndex{5}$: Identifying Tables that Represent Functions

Яка таблиця, Таблиця$\PageIndex{6}$$\PageIndex{7}$, Таблиця або Таблиця$\PageIndex{8}$, представляє функцію (якщо така є)?

Таблиця$\PageIndex{6}$
Вхідні дані	Вихід
2	1
5	3
8	6

Таблиця$\PageIndex{7}$
Вхідні дані	Вихід
-3	5
0	1
4	5

Таблиця$\PageIndex{8}$
Вхідні дані	Вихід
1	0
5	2
5	4

Рішення

Таблиця$\PageIndex{6}$ і Таблиця$\PageIndex{7}$ визначають функції. В обох випадках кожне вхідне значення відповідає рівно одному вихідному значенню. Таблиця$\PageIndex{8}$ не визначає функцію, оскільки вхідне значення 5 відповідає двом різним вихідним значенням.

Коли таблиця представляє функцію, відповідні вхідні та вихідні значення також можуть бути вказані за допомогою позначення функції.

Функція, представлена таблицею,$\PageIndex{6}$ може бути представлена записом

\[f(2)=1\text{, }f(5)=3\text{, and }f(8)=6 \nonumber\]

Аналогічно твердження

\[g(−3)=5\text{, }g(0)=1\text{, and }g(4)=5 \nonumber\]

представляють функцію в таблиці$\PageIndex{7}$.

Таблиця$\PageIndex{8}$ не може бути виражена подібним чином, оскільки вона не представляє функцію.

Вправа$\PageIndex{5}$

Чи$\PageIndex{9}$ представляє таблиця функцію?

Таблиця$\PageIndex{9}$
Вхідні дані	Вихід
1	10
2	100
3	1000

Відповідь: так

Пошук вхідних і вихідних значень функції

Коли ми знаємо вхідне значення і хочемо визначити відповідне вихідне значення для функції, ми оцінюємо функцію. Оцінювання завжди дасть один результат, оскільки кожне вхідне значення функції відповідає рівно одному вихідному значенню.

Коли ми знаємо вихідне значення і хочемо визначити вхідні значення, які будуть виробляти це вихідне значення, ми встановлюємо вихід рівним формулі функції і вирішуємо для входу. Рішення може спричинити більше одного рішення, оскільки різні вхідні значення можуть давати однакове вихідне значення.

Оцінка функцій в алгебраїчних формах

Коли у нас є функція у формі формули, це, як правило, проста справа, щоб оцінити функцію. Наприклад, функцію$f(x)=5−3x^2$ можна оцінити шляхом зведення вхідного значення в квадрат, множення на 3, а потім віднімання добутку з 5.

Як: Дано формулу для функції, оцініть.

Дано формулу для функції, оцінюють.

Замініть вхідну змінну у формулі наданим значенням.
Обчисліть результат.

Приклад$\PageIndex{6A}$: Evaluating Functions at Specific Values

1. Оцініть$f(x)=x^2+3x−4$ на

$2$
$a$
$a+h$
Оцініть$\frac{f(a+h)−f(a)}{h}$

Рішення

Замініть x у функції кожним вказаним значенням.

а Оскільки вхідним значенням є число, 2, ми можемо використовувати просту алгебру для спрощення.

\[\begin{align*}f(2)&=2^2+3(2)−4\\&=4+6−4\\ &=6\end{align*}\]

b У цьому випадку вхідним значенням є буква, тому ми не можемо спростити відповідь далі.

\[f(a)=a^2+3a−4\nonumber\]

c При вхідному значенні$a+h$, ми повинні використовувати розподільну властивість.

\[\begin{align*}f(a+h)&=(a+h)^2+3(a+h)−4\\&=a^2+2ah+h^2+3a+3h−4 \end{align*}\]

d В цьому випадку ми застосовуємо вхідні значення до функції не один раз, а потім виконуємо алгебраїчні операції над результатом. Ми вже з'ясували, що

\[f(a+h)=a^2+2ah+h^2+3a+3h−4\nonumber\]

і ми знаємо, що

\[f(a)=a^2+3a−4 \nonumber\]

Тепер об'єднаємо результати і спрощуємо.

\[\begin{align*}\dfrac{f(a+h)−f(a)}{h}&=\dfrac{(a^2+2ah+h^2+3a+3h−4)−(a^2+3a−4)}{h}\\ &=\dfrac{(2ah+h^2+3h)}{h} \\ &=\dfrac{h(2a+h+3)}{h} & &\text{Factor out h.}\\ &=2a+h+3 & & \text{Simplify.}\end{align*}\]

Приклад$\PageIndex{6B}$: Evaluating Functions

З огляду на функцію$h(p)=p^2+2p$, оцінюємо$h(4)$.

Рішення

Для оцінки$h(4)$ підставляємо значення 4 для вхідної змінної p в задану функцію.

\[\begin{align*}h(p)&=p^2+2p\\h(4)&=(4)^2+2(4)\\ &=16+8\\&=24\end{align*}\]

Тому для входу 4 ми маємо вихід 24.

Вправа$\PageIndex{6}$

З огляду на функцію$g(m)=\sqrt{m−4}$, оцінюємо$g(5)$.

Відповідь: $g(5)=1$

Приклад$\PageIndex{7}$: Solving Functions

З огляду на функцію$h(p)=p^2+2p$, вирішуйте для$h(p)=3$.

Рішення

\[\begin{array}{rl} h(p)=3\\p^2+2p=3 & \text{Substitute the original function}\\ p^2+2p−3=0 & \text{Subtract 3 from each side.}\\(p+3)(p−1)=0&\text{Factor.}\end{array} \nonumber \]

Якщо$(p+3)(p−1)=0$, або$(p+3)=0$ або$(p−1)=0$ (або обидва вони рівні$0$). Ми встановимо кожен коефіцієнт рівним$0$ і вирішимо для кожного$p$ випадку.

\[(p+3)=0,\; p=−3 \nonumber \]

\[(p−1)=0,\, p=1 \nonumber\]

Це дає нам два рішення. Вихід,$h(p)=3$ коли вхід є$p=1$ або$p=−3$. Ми також можемо перевірити за допомогою графіків, як на малюнку$\PageIndex{6}$. Графік перевіряє, що$h(1)=h(−3)=3$ і$h(4)=24$.

[Графік параболи з позначеними точками (-3, 3), (1, 3) та (4, 24).] — Малюнок$\PageIndex{6}$: Графік$h(p)=p^2+2p$

Вправа$\PageIndex{7}$

З огляду на функцію$g(m)=\sqrt{m−4}$, вирішувати$g(m)=2$.

Відповідь: $m=8$

Оцінка функцій, виражених у формулах

Деякі функції визначаються математичними правилами або процедурами, вираженими у формі рівняння. Якщо є можливість висловити висновок функції за допомогою формули, що включає вхідну величину, то ми можемо визначити функцію в алгебраїчній формі. Наприклад, рівняння$2n+6p=12$ виражає функціональну залежність між$n$ і$p$. Ми можемо переписати його, щоб вирішити$p$, чи є функцією$n$.

Як: Задано функцію у формі рівняння, запишіть її алгебраїчну формулу.

Вирішіть рівняння, щоб ізолювати вихідну змінну з одного боку знака рівності, а інша сторона як вираз, який включає лише вхідну змінну.
Використовуйте всі звичайні алгебраїчні методи для розв'язання рівнянь, такі як додавання або віднімання однакової величини з обох сторін або множення або ділення обох сторін рівняння на однакову величину.

Приклад$\PageIndex{8A}$: Finding an Equation of a Function

Висловіть відносини$2n+6p=12$ як функцію$p=f(n)$, якщо це можливо.

Рішення

Щоб висловити відносини в цій формі, нам потрібно вміти писати відносини де$p$ є функція$n$, що означає писати його як$p=[\text{expression involving }n]$.

\[\begin{align*}2n+6p&=12 \\ 6p&=12−2n && \text{Subtract 2n from both sides.} \\ p&=\dfrac{12−2n}{6} & &\text{Divide both sides by 6 and simplify.} \\ p&=\frac{12}{6}−\frac{2n}{6} \\ p&=2−\frac{1}{3}n\end{align*}\]

Тому$p$ як функція$n$ пишеться як

\[p=f(n)=2−\frac{1}{3}n \nonumber\]

Аналіз

Важливо відзначити, що не кожен зв'язок, виражений рівнянням, також може бути виражений у вигляді функції за допомогою формули.

Приклад$\PageIndex{8B}$: Expressing the Equation of a Circle as a Function

Чи$x^2+y^2=1$ являє рівняння функцію з$x$ як вхід і$y$ як вихід? Якщо так, висловіть відносини як функцію$y=f(x)$.

Рішення

Спочатку віднімаємо$x^2$ з обох сторін.

\[y^2=1−x^2 \nonumber\]

Зараз ми спробуємо вирішити для$y$ цього рівняння.

\[y=\pm\sqrt{1−x^2} \nonumber\]

\[\text{so, }y=\sqrt{1−x^2}\;\text{and}\;y = −\sqrt{1−x^2} \nonumber\]

Ми отримуємо два виходи, що відповідають одному і тому ж входу, тому цей зв'язок не може бути представлений у вигляді єдиної функції$y=f(x)$.

Вправа$\PageIndex{8}$

Якщо$x−8y^3=0$, висловити$y$ як функцію$x$.

Відповідь: $y=f(x)=\dfrac{\sqrt[3]{x}}{2}$

Q & A

Чи існують зв'язки, виражені рівнянням, які представляють функцію, але які все ще не можуть бути представлені алгебраїчною формулою?

Так, таке може статися. Наприклад, з огляду на рівняння$x=y+2^y$, якщо ми хочемо висловити y як функцію х, не існує простої алгебраїчної формули, що включає лише$x$ те, що дорівнює$y$. Однак кожен визначає$x$ унікальне значення для$y$, і існують математичні процедури, за допомогою яких$y$ можна знайти будь-яку бажану точність. У цьому випадку ми говоримо, що рівняння дає неявне (неявне)$y$ правило для функції$x$, хоча формула не може бути записана явно.

Оцінка функції, заданої в табличній формі

Як ми бачили вище, ми можемо представляти функції в таблицях. І навпаки, ми можемо використовувати інформацію в таблицях для написання функцій, і ми можемо оцінювати функції за допомогою таблиць. Наприклад, наскільки добре наші вихованці згадують приємні спогади, якими ми з ними ділимося? Існує міська легенда, що у золотої рибки пам'ять 3 секунди, але це всього лише міф. Золота рибка може запам'ятовувати до 3 місяців, в той час як бета-риба має пам'ять до 5 місяців. І поки тривалість пам'яті цуценя становить не більше 30 секунд, доросла собака може запам'ятати протягом 5 хвилин. Це мізерно в порівнянні з кішкою, тривалість пам'яті якої триває 16 годин.

Функція, яка пов'язує тип вихованця з тривалістю його періоду пам'яті, легше візуалізується за допомогою таблиці (Таблиця$\PageIndex{10}$).

Таблиця$\PageIndex{10}$
Пам'ять домашніх тварин	тривалість в годині
Щеня	0,008
Дорослий Собака	0.083
Кішка	3
Золота рибка	2160
Бета Риба	3600

Іноді оцінка функції в табличній формі може бути більш корисною, ніж використання рівнянь. Тут викликаємо функцію$P$. Домен функції - це тип вихованця, а діапазон - дійсне число, яке представляє кількість годин тривалості пам'яті вихованця. Ми можемо оцінити функцію$P$ за вхідним значенням «золотої рибки». Ми б написали$P(goldfish)=2160$. Зверніть увагу, що для оцінки функції в табличній формі ми ідентифікуємо вхідне значення і відповідне вихідне значення з відповідного рядка таблиці. Таблична форма для функції P здається ідеально підходить для цієї функції, більше, ніж запис її у формі абзацу або функції.

Як: За допомогою функції, представленої таблицею, визначити конкретні вихідні та вхідні значення

1. Знайдіть дані вхідні дані в рядку (або стовпці) вхідних значень.
2. Визначте відповідне вихідне значення в парі з цим вхідним значенням.
3. Знайдіть задані вихідні значення в рядку (або стовпці) вихідних значень, відзначаючи щоразу, коли з'являється вихідне значення.
4. Визначте вхідне значення (и), що відповідає заданому вихідному значенню.

Приклад$\PageIndex{9}$: Evaluating and Solving a Tabular Function

Використовуючи таблицю$\PageIndex{11}$,

а. оцінювати$g(3)$.
б. вирішувати$g(n)=6$.

Таблиця$\PageIndex{11}$
$n$	1	2	3	4	5
$g(n)$	8	6	7	6	8

Рішення

a. оцінка$g(3)$ означає визначення вихідного значення функції$g$ для вхідного значення$n=3$. Вихідне значення таблиці,$n=3$ відповідне 7, так що$g(3)=7$.
b. рішення$g(n)=6$ означає ідентифікацію вхідних значень, n, які дають вихідне значення 6. $\PageIndex{12}$У таблиці наведено два рішення: 2 і 4.

Таблиця$\PageIndex{12}$
$n$	1	2	3	4	5
$g(n)$	8	6	7	6	8

Коли ми вводимо 2 в функцію$g$, наш вихід 6. Коли ми вводимо 4 в функцію$g$, наш вихід також 6.

Вправа$\PageIndex{1}$

Використовуючи таблицю$\PageIndex{12}$, оцінюйте$g(1)$.

Відповідь: $g(1)=8$

Пошук значень функцій з графіка

Оцінка функції за допомогою графіка також вимагає знаходження відповідного вихідного значення для заданого вхідного значення, тільки в цьому випадку ми знаходимо вихідне значення, дивлячись на графік. Розв'язування рівняння функції за допомогою графіка вимагає знаходження всіх екземплярів заданого вихідного значення на графіку та спостереження за відповідним вхідним значенням (-ами).

Приклад$\PageIndex{10}$: Reading Function Values from a Graph

З огляду на графік на малюнку$\PageIndex{7}$,

Оцініть$f(2)$.
Вирішити$f(x)=4$.

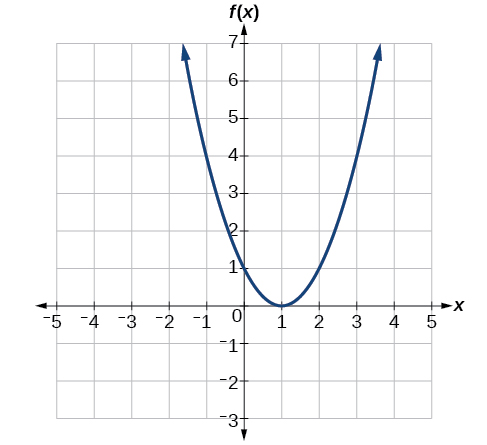
Графік додатної параболи з центром (1, 0) — Малюнок$\PageIndex{7}$: Графік додатної параболи з центром у$(1, 0)$.

Рішення

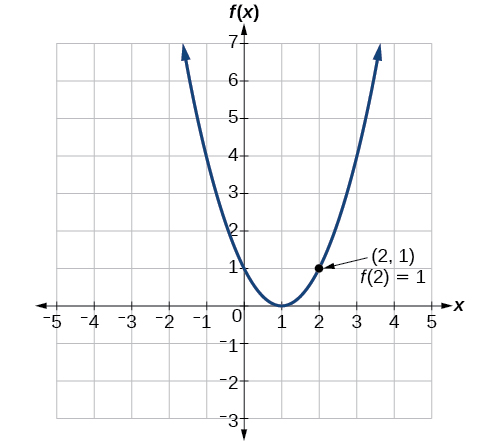
Щоб оцінити$f(2)$, знайдіть точку на кривій де$x=2$, а потім прочитайте y-координату цієї точки. Точка має координати$(2,1)$, так що$f(2)=1$. Див$\PageIndex{8}$. Малюнок.

Графік додатної параболи з центром (1, 0) з міченою точкою (2, 1), де f (2) =1. — $\PageIndex{8}$: Графік додатної параболи з центром з$(1, 0)$ міченою точкою$(2, 1)$ де$f(2) =1$.

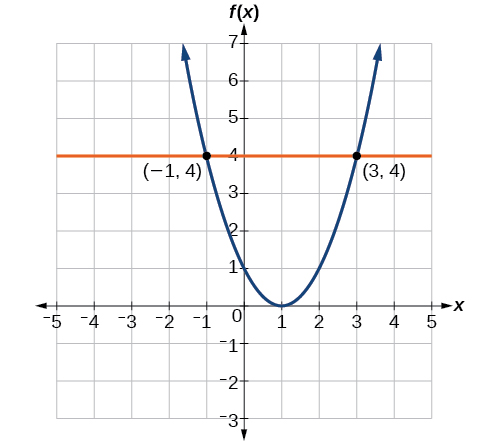
Для вирішення$f(x)=4$ знаходимо вихідне значення 4 на вертикальній осі. Рухаючись горизонтально по лінії$y=4$, знаходимо дві точки кривої з вихідним значенням 4:$(−1,4)$ і$(3,4)$. Ці пункти представляють два розв'язки$f(x)=4$: −1 або 3. Це означає, що$f(−1)=4$ і$f(3)=4$, або, якщо вхідним буде −1 або 3, вивід дорівнює 4. Див$\PageIndex{9}$. Малюнок.

Графік параболи, зверненої вгору, з вершиною в (0,1) і маркованими точками в (-1, 4) і (3,4). Лінія з y = 4 перетинає параболу в маркованих точках. — Малюнок$\PageIndex{9}$: Графік параболи, зверненої вгору, з вершиною в$(0,1)$ і з позначеними точками в$(-1, 4)$ і$(3,4)$. Лінія в$y = 4$ перетинає параболу в мічених точках.

Вправа$\PageIndex{10}$

З огляду на графік на малюнку$\PageIndex{7}$, вирішуйте$f(x)=1$.

Відповідь: $x=0$або$x=2$

Визначення того, чи є функція один-на-один

Деякі функції мають задане вихідне значення, яке відповідає двом або більше вхідним значенням. Наприклад, на графіку акцій, показаному на малюнку на початку цього розділу, ціна акцій становила 1000 доларів на п'ять різних дат, що означає, що було п'ять різних вхідних значень, які призвели до однакового вихідного значення 1000 доларів.

Однак деякі функції мають лише одне вхідне значення для кожного вихідного значення, а також мають лише один вихід для кожного входу. Ми називаємо ці функції один-на-один. Як приклад розглянемо школу, яка використовує лише літерні оцінки та десяткові еквіваленти, як зазначено в табл$\PageIndex{13}$.

Таблиця$\PageIndex{13}$: Літерні сорти та десяткові еквіваленти.
Лист Оцінка	Середній бал
A	4.0
Б	3.0
C	2.0
D	1.0

Ця система оцінювання представляє функцію «один до одного», оскільки кожне введення літер дає один певний середній результат балів, а кожне середнє значення балів відповідає одній вхідній літері.

Щоб візуалізувати цю концепцію, давайте знову подивимося на дві прості функції, намальовані на малюнках$\PageIndex{1a}$ і$\PageIndex{1b}$. Функція в частині (а) показує зв'язок, який не є функцією один до одного, оскільки входи$q$ і$r$ обидва дають вихід$n$. Функція в частині (b) показує зв'язок, який є функцією один до одного, оскільки кожен вхід пов'язаний з одним виходом.

Функції «один-на-один»

Функція один до одного - це функція, в якій кожне вихідне значення відповідає рівно одному вхідному значенню.

Приклад$\PageIndex{11}$: Determining Whether a Relationship Is a One-to-One Function

Чи є площа кола функцією його радіуса? Якщо так, чи є функція один-на-один?

Рішення

Коло радіуса$r$ має унікальну міру площі$A={\pi}r^2$, задану, тому для будь-якого входу$r$, є тільки один вихід,$A$. Площа є функцією радіуса$r$.

Якщо функція один-на-один, вихідне значення, площа, має відповідати унікальному вхідному значенню - радіусу. Будь-яка міра площі$A$ задається за формулою$A={\pi}r^2$. Оскільки області та радіуси є додатними числами, існує рівно одне рішення:$\sqrt{\frac{A}{\pi}}$. Таким чином, площа кола є один до одного функція радіуса кола.

Вправа$\PageIndex{11A}$

Чи є баланс функцією номера банківського рахунку?
Чи є номер банківського рахунку функцією балансу?
Чи є баланс функцією «один-на-один» номера банківського рахунку?

Відповідь

a. так, тому що кожен банківський рахунок має єдиний залишок в будь-який момент часу;

b. ні, тому що кілька номерів банківських рахунків можуть мати однаковий баланс;

c. ні, тому що один і той же вихід може відповідати більш ніж одному входу.

Вправа$\PageIndex{11B}$

Оцініть наступне:

Якщо кожен відсоток оцінку, зароблений на курсі, перекладається на одну букву, чи є оцінка букви функцією відсотка?
Якщо так, то чи є функція один-на-один?

Відповідь: а. так, клас літери - це функція відсотка класу;
б. Ні, це не один до одного. Є 100 різних відсотків чисел, які ми могли б отримати, але лише близько п'яти можливих класів літер, тому не може бути лише один відсоток числа, який відповідає кожному класу букв.

Використання тесту вертикальної лінії

Як ми бачили в деяких прикладах вище, ми можемо представляти функцію за допомогою графіка. Графіки відображають безліч пар введення-виведення в невеликому просторі. Візуальна інформація, яку вони надають, часто полегшує розуміння відносин. За умовністю графіки зазвичай будуються з вхідними значеннями вздовж горизонтальної осі та вихідними значеннями вздовж вертикальної осі.

Найбільш поширені графіки називають вхідне значення$x$ і вихід$y$, і ми говоримо, що$y$ це функція$x$, або$y=f(x)$ коли функція називається$f$. Графік функції - це множина всіх точок$(x,y)$ на площині, яка задовольняє рівнянню$y=f(x)$. Якщо функція визначена лише для декількох вхідних значень, то графіком функції є лише кілька точок, де координата x кожної точки є вхідним значенням, а y-координата кожної точки - відповідним вихідним значенням. Наприклад, чорні точки на графіку на малюнку$\PageIndex{10}$ говорять нам про те, що$f(0)=2$ і$f(6)=1$. Однак множина всіх точок,$y=f(x)$ що$(x,y)$ задовольняють, є кривою. Показана крива включає$(0,2)$ і$(6,1)$ тому, що крива проходить через ці точки

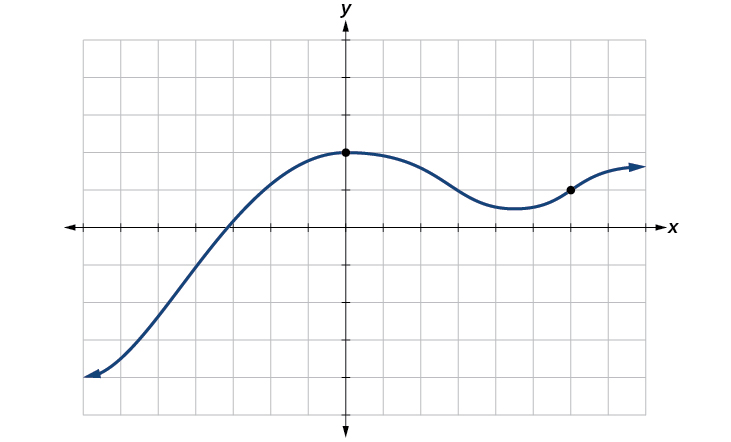
Малюнок$\PageIndex{10}$: Графік многочлена.

Тест вертикальної лінії може бути використаний для визначення того, чи відповідає графік функції. Якщо ми можемо намалювати будь-яку вертикальну лінію, яка перетинає графік більше одного разу, то графік не визначає функцію, оскільки функція має лише одне вихідне значення для кожного вхідного значення. Див$\PageIndex{11}$. Малюнок.

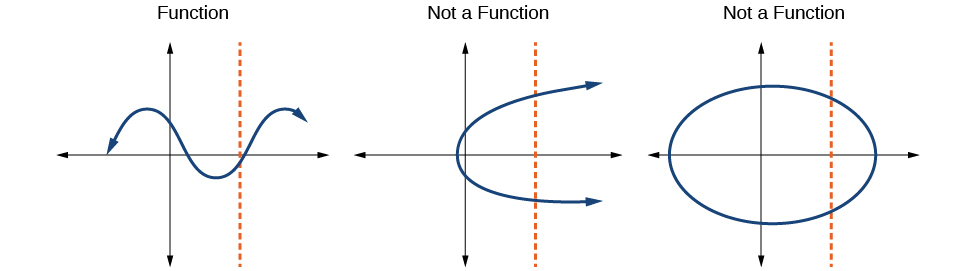
Три графіки наочно показують, що є, а що не є функцією. — Малюнок$\PageIndex{11}$: Три графіки наочно показують, що є і не є функцією.

Howto: За допомогою графіка використовуйте тест вертикальної лінії, щоб визначити, чи є графік функцією

Перевірте графік, щоб побачити, чи будь-яка намальована вертикальна лінія перетинає криву більше одного разу.
Якщо така лінія є, визначте, що графік не представляє функцію.

Приклад$\PageIndex{12}$: Applying the Vertical Line Test

Які з графіків на малюнку$\PageIndex{12}$ представляють (и) функцію$y=f(x)$?

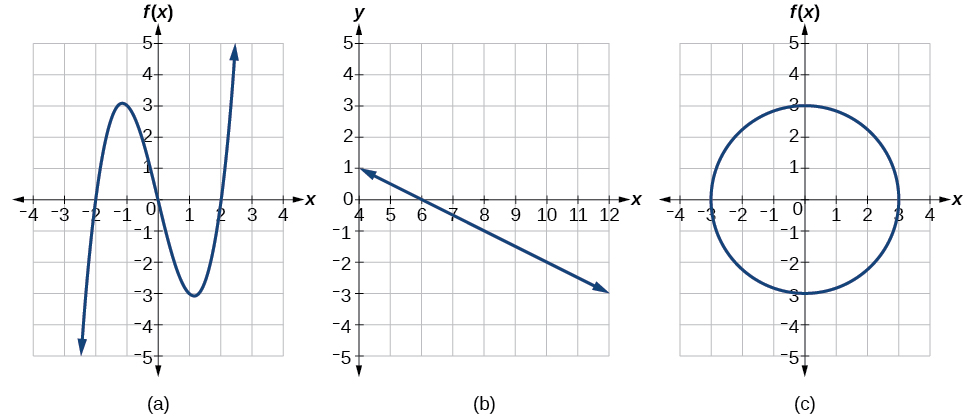
Рисунок$\PageIndex{12}$: Графік многочлена (a), похилої вниз лінії (b) та кола (c).

Рішення

Якщо будь-яка вертикальна лінія перетинає графік більше одного разу, відношення, представлене графіком, не є функцією. Зверніть увагу, що будь-яка вертикальна лінія буде проходити лише через одну точку з двох графіків, показаних у частинок (a) та (b) малюнка$\PageIndex{12}$. З цього можна зробити висновок, що ці два графіки представляють функції. Третій графік не представляє функцію, оскільки при максимальному значенні x вертикальна лінія перетинає графік у більш ніж одній точці, як показано на малюнку$\PageIndex{13}$.

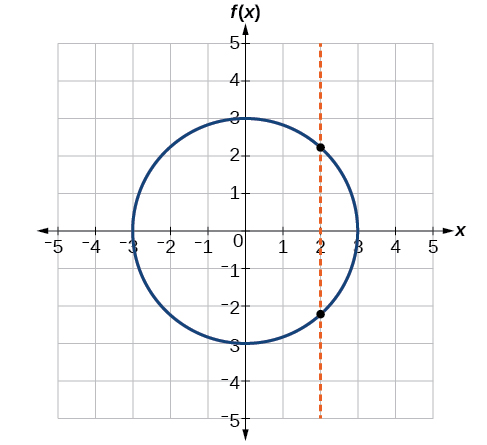
Вправа$\PageIndex{12}$

Чи є графік на$\PageIndex{14}$ малюнку функцію?

[Абсолютна функція f (x) =|x|.] — Рисунок$\PageIndex{14}$: Графік функції абсолютного значення.

Відповідь: так

Використання тесту горизонтальної лінії

Після того, як ми визначили, що графік визначає функцію, простий спосіб визначити, чи є це функція один до одного, є використання тесту горизонтальної лінії. Намалюйте горизонтальні лінії через графік. Якщо будь-яка горизонтальна лінія перетинає графік більше одного разу, то графік не представляє функцію один до одного.

Інструкція: З огляду на графік функції, скористайтеся тестом горизонтальної лінії, щоб визначити, чи є графік функцією один до одного

Перевірте графік, щоб побачити, чи будь-яка намальована горизонтальна лінія перетинає криву більше одного разу.
Якщо є якась така лінія, визначте, що функція не один-на-один.

Приклад$\PageIndex{13}$: Applying the Horizontal Line Test

Розглянемо функції, наведені на малюнку$\PageIndex{12a}$ і малюнку$\PageIndex{12b}$. Чи є будь-яка з функцій один до одного?

Рішення

Функція на малюнку не$\PageIndex{12a}$ є один-на-один. Горизонтальна лінія, показана на малюнку,$\PageIndex{15}$ перетинає графік функції в двох точках (і ми навіть можемо знайти горизонтальні лінії, які перетинають її в трьох точках.)

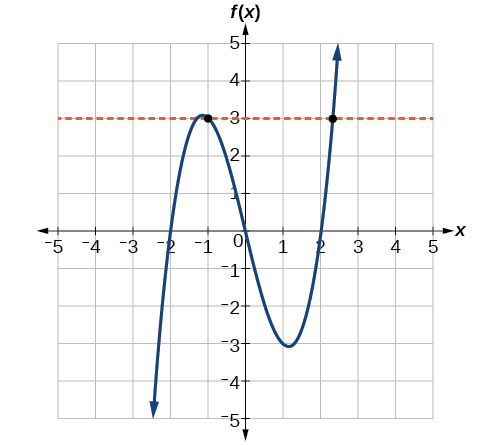
Графік многочлена з горизонтальною лінією, що перетинається через 2 точки — Малюнок$\PageIndex{15}$: Графік многочлена з горизонтальною лінією, що перетинає через 2 точки

Функція на малюнку$\PageIndex{12b}$ є один до одного. Будь-яка горизонтальна лінія буде перетинати діагональну лінію не більше одного разу.

Вправа$\PageIndex{13}$

Чи є графік, показаний на малюнку$\PageIndex{13}$ один до одного?

Відповідь: Ні, тому що вона не проходить тест горизонтальної лінії.

Визначення основних функцій інструментарію

У цьому тексті ми будемо вивчати функції - форми їх графіків, їх унікальні характеристики, їх алгебраїчні формули та способи вирішення проблем з ними. Навчаючись читати, починаємо з алфавіту. Навчаючись робити арифметику, починаємо з чисел. При роботі з функціями так само корисно мати базовий набір елементів будівельного блоку. Ми називаємо їх «функціями інструментарію», які утворюють набір основних іменованих функцій, для яких ми знаємо графік, формулу та спеціальні властивості. Деякі з цих функцій запрограмовані на окремі кнопки на багатьох калькуляторах. Для цих визначень ми будемо використовувати x як вхідну змінну і$y=f(x)$ як вихідну змінну.

Ми будемо бачити ці функції інструментарію, комбінації функцій інструментарію, їх графіки та їх перетворення часто у цій книзі. Буде дуже корисно, якщо ми зможемо швидко розпізнати ці функції інструментарію та їх функції за назвою, формулою, графіком та основними властивостями таблиці. Графіки та зразки значень таблиці включені до кожної функції, наведеної в табл$\PageIndex{14}$.

Таблиця$\PageIndex{14}$: Функції інструментарію
Ім'я	Функція	Графік
Постійна	$f(x)=c$де$c$ константа	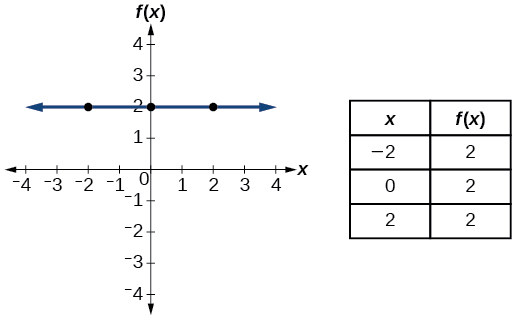$альт$
Ідентичність	$f(x)=x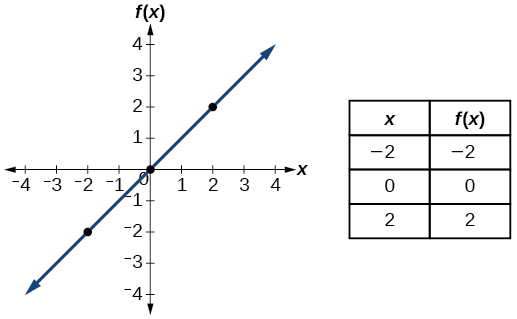$	$альт$
Абсолютна величина	$f(x)=\|x\|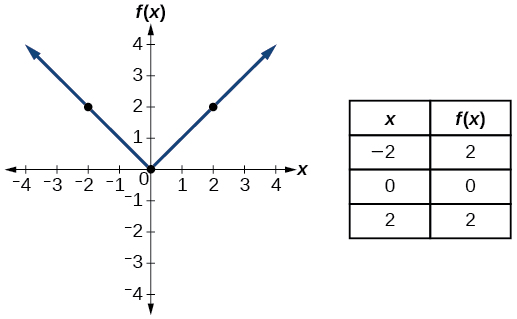$	$альт$
Квадратичний	$f(x)=x^2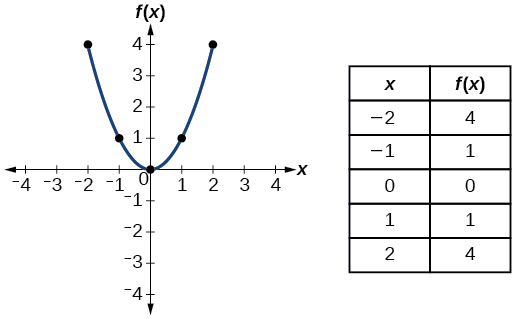$	$альт$
Кубічний	$f(x)=x^3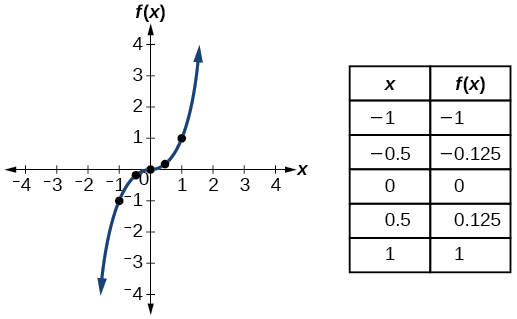$	$альт$
зворотний	$f(x)=\dfrac{1}{x}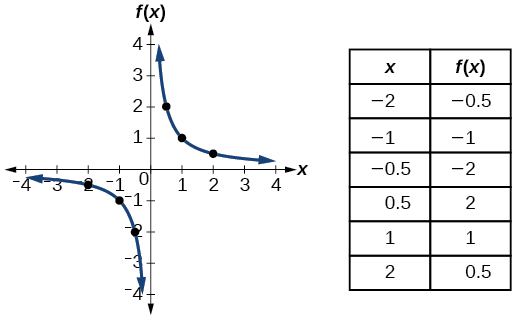$	$альт$
Зворотний квадрат	$f(x)=\dfrac{1}{x^2}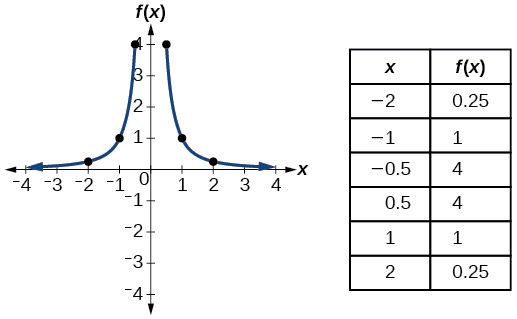$	$альт$
Квадратний корінь	$f(x)=\sqrt{x}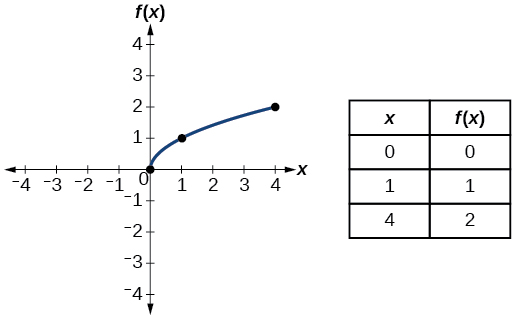$	$альт$
Кубик корінь	$f(x)=\sqrt[3]{x}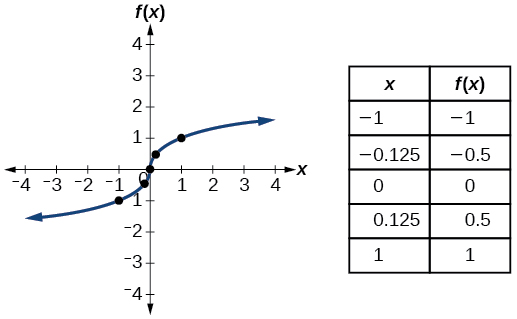$	$альт$

Ключові рівняння

Постійна функція$f(x)=c$,$c$ де константа
Функція ідентичності$f(x)=x$
Функція абсолютного значення$f(x)=|x|$
Квадратична функція$f(x)=x^2$
Кубічна функція$f(x)=x^3$
взаємна функція$f(x)=\dfrac{1}{x}$
Взаємна квадратна функція$f(x)=\frac{1}{x^2}$
Функція квадратного кореня$f(x)=\sqrt{x}$
Функція кореня куба$f(x)=3\sqrt{x}$

Ключові поняття

Відношення - це набір впорядкованих пар. Функція - це певний тип зв'язку, в якому кожне значення домену, або вхід, призводить до рівно одного значення діапазону, або виводу.
Позначення функції - це скорочений метод зв'язку вхідних даних з виходом у вигляді$y=f(x)$.
У табличній формі функція може бути представлена рядками або стовпцями, які відносяться до вхідних і вихідних значень.
Для оцінки функції визначаємо вихідне значення для відповідного вхідного значення. Алгебраїчні форми функції можуть бути оцінені шляхом заміни вхідної змінної на задане значення.
Для вирішення для конкретного значення функції визначаємо вхідні значення, які дають конкретне вихідне значення.
Алгебраїчну форму функції можна записати з рівняння.
Вхідні та вихідні значення функції можуть бути визначені з таблиці.
Співвідношення вхідних значень до вихідних значень на графіку є ще одним способом оцінки функції.
Функція є один до одного, якщо кожне вихідне значення відповідає лише одному вхідному значенню.
Графік являє собою функцію, якщо будь-яка вертикальна лінія, намальована на графіку, перетинає графік не більше ніж в одній точці.
Графік функції один до одного проходить тест горизонтальної лінії.

Виноски

1 http://www.baseball-almanac.com/lege... /лісн100.штмл. Доступ до 24.03.2014.
2 www.kgbanswers.com/як-довго-я... y-span/4221590. Доступ до 24.03.2014.

Глосарій

залежна
змінна вихідна змінна

domain
- множина всіх можливих вхідних значень для відношення

функція
- відношення, в якому кожне вхідне значення дає унікальне вихідне значення

тест
горизонтальної лінії - метод перевірки того, чи є функція один-на-один, визначаючи, чи перетинає будь-яка горизонтальна лінія графік більше одного разу

незалежна
змінна вхідна змінна

введіть кожен об'єкт або значення в області, яка відноситься до іншого об'єкта або значення за допомогою зв'язку, відомого як функція

функція
one-to-one - функція, для якої кожне значення виводу пов'язане з унікальним вхідним значенням

вивести
кожен об'єкт або значення в діапазоні, який утворюється при введенні вхідного значення у функцію

діапазон
набору вихідних значень, які є результатом вхідних значень у співвідношенні

відношення
- набір впорядкованих пар

тест вертикальної лінії
- метод перевірки того, чи є граф функцією, визначаючи, чи перетинає вертикальна лінія графік не більше одного разу.

Номер місяця,\(m\) (вхід)	1	2	3	4	5	6	7	8	9	10	11	12
Днів у місяці,\(D\) (вихідний)	31	28	31	30	31	30	31	31	30	31	30	31

Вік в роках,\(a\) (вхід)	5	5	6	7	8	9	10
Висота в дюймах,\(h\) (вихід)	40	42	44	47	50	52	54

Ім'я	Функція	Графік
Постійна	\(f(x)=c\)де\(c\) константа	$альт$
Ідентичність	\(f(x)=x\)	$альт$
Абсолютна величина	\(f(x)=\|x\|\)	$альт$
Квадратичний	\(f(x)=x^2\)	$альт$
Кубічний	\(f(x)=x^3\)	$альт$
зворотний	\(f(x)=\dfrac{1}{x}\)	$альт$
Зворотний квадрат	\(f(x)=\dfrac{1}{x^2}\)	$альт$
Квадратний корінь	\(f(x)=\sqrt{x}\)	$альт$
Кубик корінь	\(f(x)=\sqrt[3]{x}\)	$альт$

Таблиця\(\PageIndex{4}\): Функція\(Q=g(n)\)
\(n\)	1	2	3	4	5
\(Q\)	8	6	7	6	8

Таблиця\(\PageIndex{11}\)
\(n\)	1	2	3	4	5
\(g(n)\)	8	6	7	6	8

Таблиця\(\PageIndex{12}\)
\(n\)	1	2	3	4	5
\(g(n)\)	8	6	7	6	8