3.6: Трансформація функцій

Last updated
Save as PDF

Page ID: 59634

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Функції графа з використанням вертикальних і горизонтальних зсувів.
Функції графіка використовують відображення навколо осі x та осі y.
Визначте, чи є функція парною, непарною чи ні, з її графіка.
Графік функціонує за допомогою стискань і розтяжок.
Поєднуйте перетворення.

Всі ми знаємо, що плоске дзеркало дозволяє нам бачити точне зображення себе і того, що знаходиться позаду нас. Коли ми нахиляємо дзеркало, зображення, які ми бачимо, можуть зміщуватися горизонтально або вертикально. Але що відбувається, коли ми згинаємо гнучке дзеркало? Як і карнавальне дзеркало для веселощів, воно представляє нам спотворене зображення себе, розтягнуте або стиснене горизонтально чи вертикально. Подібним чином ми можемо спотворювати або трансформувати математичні функції, щоб краще адаптувати їх до опису об'єктів чи процесів у реальному світі. У цьому розділі ми розглянемо кілька видів перетворень.

альт — Малюнок$\PageIndex{1}$: (Кредит: «Місько» /Flickr)

Часто, коли задається задача, ми намагаємося змоделювати сценарій за допомогою математики у вигляді слів, таблиць, графіків і рівнянь. Один із методів, який ми можемо використовувати, - адаптувати основні графіки функцій інструментарію для побудови нових моделей для заданого сценарію. Існують систематичні способи зміни функцій для побудови відповідних моделей для проблем, які ми намагаємося вирішити.

Визначення вертикальних зрушень

Один простий вид перетворення передбачає зміщення всього графіка функції вгору, вниз, вправо або вліво. Найпростіший зсув - це вертикальний зсув, переміщення графіка вгору або вниз, оскільки це перетворення передбачає додавання позитивної або негативної константи до функції. Іншими словами, ми додаємо одну і ту ж константу до вихідного значення функції незалежно від вхідних даних. Для функції функція$g(x)=f(x)+k$$f(x)$ зсувається вертикально$k$ одиницями. Див. Рисунок$\PageIndex{2}$ для прикладу.

Вертикальний зсув на k=1 функції кореня куба f (x) =3√x. — Рисунок$\PageIndex{2}$: Вертикальний$k=1$ зсув на функцію кореня куба$f(x)=\sqrt[3]{x}$.

Щоб допомогти вам візуалізувати концепцію вертикального зсуву, врахуйте це$y=f(x)$. Тому$f(x)+k$ рівнозначний$y+k$. Кожна одиниця$y$ замінюється на$y+k$, тому$y$ -value збільшується або зменшується в залежності від значення$k$. В результаті виходить зсув вгору або вниз.

Визначення: Вертикальний зсув

Задана функція$f(x)$, нова функція$g(x)=f(x)+k$, де$k$ константа, є вертикальним зсувом функції$f(x)$. Всі вихідні значення змінюються за$k$ одиницями. Якщо$k$ позитивний, графік зміститься вгору. Якщо$k$ негативний, графік зміститься вниз.

Приклад$\PageIndex{1}$: Adding a Constant to a Function

Щоб регулювати температуру в зеленій будівлі, вентиляційні отвори для повітряного потоку біля даху відкриваються і закриваються протягом дня. $\PageIndex{3}$На малюнку показана площа відкритих вентиляційних отворів$V$ (в квадратних футах) протягом усього дня в години після півночі$t$. Протягом літа менеджер об'єктів вирішує спробувати краще регулювати температуру, збільшивши кількість відкритих вентиляційних отворів на 20 квадратних футів протягом дня і ночі. Намалюйте графік цієї нової функції.

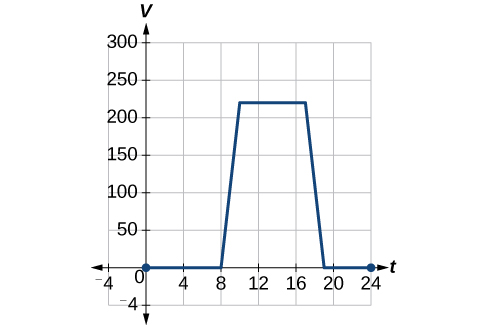
Рішення

Ми можемо намалювати графік цієї нової функції, додавши 20 до кожного з вихідних значень вихідної функції. Це матиме ефект зрушення графіка вертикально вгору, як показано на малюнку$\PageIndex{4}$.

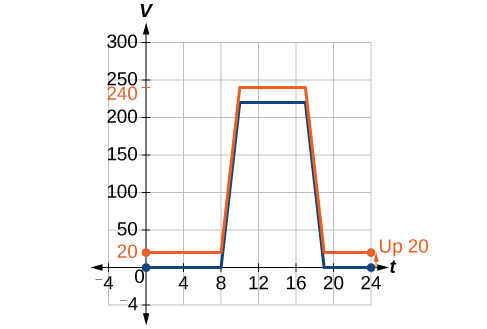
Зверніть увагу, що на малюнку$\PageIndex{4}$, для кожного вхідного значення, вихідне значення збільшилася на 20, так що, якщо ми називаємо нову функцію$S(t)$, ми могли б написати

\[S(t)=V(t)+20\]

Це позначення говорить нам, що для будь-якого значення$t$,$S(t)$ можна знайти, оцінюючи функцію$V$ на тому ж вході, а потім додаючи 20 до результату. Це визначає$S$ як перетворення функції$V$, в даному випадку вертикальний зсув вгору на 20 одиниць. Зверніть увагу, що при вертикальному зсуві вхідні значення залишаються однаковими і змінюються лише вихідні значення. Див$\PageIndex{1}$. Таблицю.

Таблиця$\PageIndex{1}$
$t$	0	8	10	17	19	24
$V(t)$	0	0	220	220	0	0
$S(t)$	20	20	240	240	20	20

Як...

Задано табличну функцію, створіть новий рядок для представлення вертикального зсуву.

Визначте вихідний рядок або стовпець.
Визначте величину зсуву.
Додайте зсув до значення в кожній вихідній комірці. Додайте додатне значення для «вгору» або від'ємне значення для «вниз».

Приклад$\PageIndex{2}$: Shifting a Tabular Function Vertically

Функція$f(x)$ наведена в табл$\PageIndex{2}$. Створіть таблицю для функції$g(x)=f(x)−3$.

Таблиця$\PageIndex{2}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

Рішення

Формула$g(x)=f(x)−3$ говорить нам, що ми можемо знайти вихідні значення,$g$ віднімаючи 3 з вихідних значень$f$. Наприклад:

\[\begin{align*} f(x)&=1 &\text{Given} \\[4pt] g(x)&=f(x)-3 &\text{Given Transformation} \\[4pt] g(2) & =f(2)−3 \\ &=1-3\\ &=-2\end{align*}\]

Віднімаючи 3 з кожного$f(x)$ значення, ми можемо заповнити таблицю значень для$g(x)$ як показано в табл$\PageIndex{3}$.

Таблиця$\PageIndex{3}$
$x$	2	4	6	8
$f(x)$	1	3	7	11
$g(x)$	-2	0	4	8

Аналіз

Як і у випадку з попереднім вертикальним зсувом, зверніть увагу, що вхідні значення залишаються незмінними, і змінюються лише вихідні значення.

Вправа$\PageIndex{1}$

Функція$h(t)=−4.9t^2+30t$ дає$h$ висоту кулі (в метрах), кинутого вгору від землі через$t$ секунди. Припустимо, куля замість цього був кинутий з вершини 10-метрової будівлі. $b(t)$Зв'яжіть цю нову функцію висоти$h(t)$, а потім знайдіть формулу для$b(t)$.

Відповідь: $b(t)=h(t)+10=−4.9t^2+30t+10$

Визначення горизонтальних зрушень

Ми щойно побачили, що вертикальний зсув - це зміна на виході, або зовні, функції. Тепер ми розглянемо, як зміни вхідних даних, на внутрішній стороні функції, змінюють її графік і значення. Зсув до вхідних даних призводить до переміщення графіка функції вліво або вправо в тому, що відомо як горизонтальний зсув, показаний на малюнку$\PageIndex{4}$.

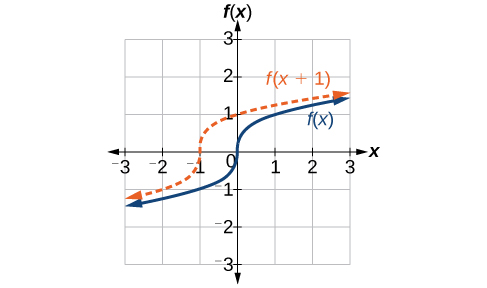
Наприклад, if$f(x)=x^2$, то$g(x)=(x−2)^2$ це нова функція. Кожен вхід зменшується на 2 перед квадратом функції. Результатом є те, що графік зміщений на 2 одиниці вправо, тому що нам потрібно буде збільшити попередній вхід на 2 одиниці, щоб отримати те саме вихідне значення, що вказано в$f$.

Визначення: Горизонтальний зсув

З огляду на функцію$f$, нова функція$g(x)=f(x−h)$, де$h$ константа, є горизонтальним зсувом функції$f$. Якщо$h$ позитивний, графік зміститься вправо. Якщо$h$ від'ємний, графік зміститься вліво.

Приклад$\PageIndex{4}$: Adding a Constant to an Input

Повертаючись до нашого прикладу повітряного потоку будівлі з малюнка$\PageIndex{2}$, припустимо, що восени менеджер об'єктів вирішує, що початковий план вентиляції починається занадто пізно, і хоче розпочати всю програму вентиляції на 2 години раніше. Намалюйте графік нової функції.

Рішення

Ми можемо встановити$V(t)$, щоб бути оригінальною програмою і$F(t)$ бути переглянутою програмою.

\[V(t)= \text{ the original venting plan} \nonumber\]

\[F(t)= \text{ starting 2 hrs sooner} \nonumber\]

На новому графіку кожен раз потік повітря такий же, як і вихідна функція$V$ була через 2 години. Наприклад, у вихідній функції$V$ потік повітря починає змінюватися о 8 годині ранку, тоді як для функції$F$ потік повітря починає змінюватися о 6 годині ранку$V(8)=F(6)$. Див$\PageIndex{5}$. Малюнок. Зверніть увагу також, що вентиляційні отвори вперше відкрилися$220 \text{ft}^2$ о 10 годині ранку за початковим планом, тоді як за новим планом вентиляційні отвори досягають$220 \text{ft}^2$ о 8 ранку, так що$V(10)=F(8)$.

В обох випадках ми бачимо це, тому що$F(t)$ починається на 2 години раніше,$h=−2$. Це означає, що однакові вихідні значення досягаються, коли$F(t)=V(t−(−2))=V(t+2)$.

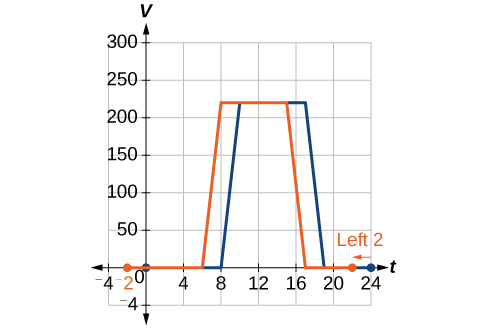
Аналіз

Зверніть увагу, що$V(t+2)$ має ефект зрушення графіка вліво.

Горизонтальні зміни або «внутрішні зміни» впливають на область функції (вхід) замість діапазону і часто здаються контрінтуїтивними. Нова функція$F(t)$ використовує ті ж виходи, що і$V(t)$, але відповідає цим виходам на входи на 2 години раніше, ніж ті з$V(t)$. Сказавши інший спосіб, ми повинні додати 2 години на вхід,$V$ щоб знайти відповідний вихід для$F:F(t)=V(t+2)$.

Як...

Задано табличну функцію, створіть новий рядок для представлення горизонтального зсуву.

Визначте вхідний рядок або стовпець.
Визначте величину зсуву.
Додайте зсув до значення в кожній вхідній комірці.

Приклад$\PageIndex{5}$: Shifting a Tabular Function Horizontally

Функція$f(x)$ наведена в табл$\PageIndex{4}$. Створіть таблицю для функції$g(x)=f(x−3)$.

Таблиця$\PageIndex{4}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

Рішення

Формула$g(x)=f(x−3)$ говорить нам, що вихідні значення$g$ збігаються з вихідним значенням,$f$ коли вхідне значення на 3 менше вихідного значення. Наприклад, ми це знаємо$f(2)=1$. Щоб отримати такий же вихід з функції$g$, нам знадобиться вхідне значення, яке на 3 більше. Ми вводимо значення, яке 3 більше для$g(x)$ тому, що функція забирає 3, перш ніж оцінювати функцію$f$.

\[\begin{align*} g(5)&=f(5-3) \\ &=f(2) \\ &=1 \end{align*}\]

Продовжуємо з іншими значеннями, щоб створити Таблицю$\PageIndex{5}$.

Таблиця$\PageIndex{5}$
$x$	5	7	9	11
$x-3$	2	4	6	8
$f(x)$	1	3	7	11
$g(x)$	1	3	7	11

Результатом є те, що функція$g(x)$ була зрушена вправо на 3. Зверніть увагу, що вихідні значення для$g(x)$ залишаються такими ж, як вихідні значення для$f(x)$, але відповідні вхідні значення$x$, зміщені вправо на 3. Зокрема, 2 змістився на 5, 4 зміщений на 7, 6 зміщений на 9, а 8 зміщений на 11.

Аналіз

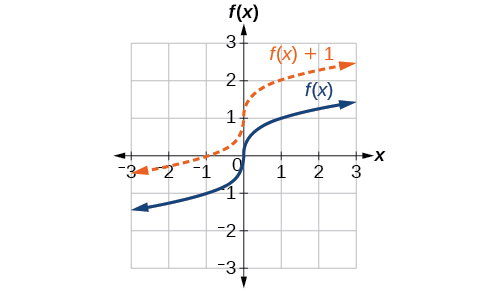
Малюнок$\PageIndex{6}$ представляє обидві функції. Ми бачимо горизонтальний зсув у кожній точці.

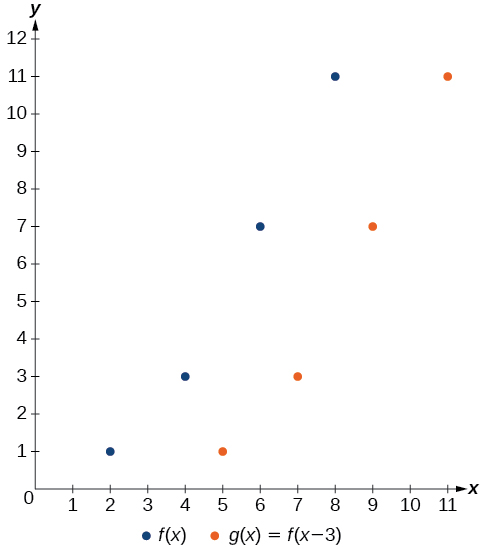
Графік точок з попередньої таблиці для f (x) та g (x) =f (x-3) — Малюнок$\PageIndex{6}$: Графік точок з попередньої таблиці для$f(x)$ і$g(x)=f(x-3)$

Приклад$\PageIndex{6}$: Identifying a Horizontal Shift of a Toolkit Function

Рисунок$\PageIndex{7}$ представляє перетворення функції інструментарію$f(x)=x^2$. Пов'язати цю нову функцію$g(x)$$f(x)$, а потім знайти формулу для$g(x)$.

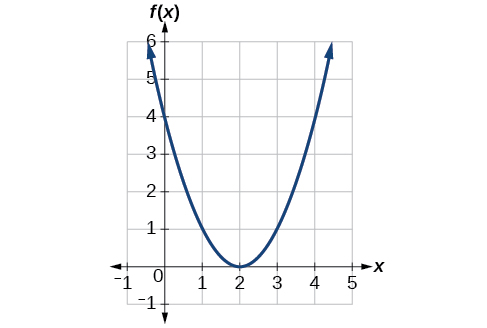
Рішення

Зверніть увагу, що графік ідентичний за формою$f(x)=x^2$ функції, але$x$ -значення зміщені вправо на 2 одиниці. Вершина колись була в$(0,0)$, але тепер вершина знаходиться в$(2,0)$. Графік являє собою основну квадратичну функцію, зміщену на 2 одиниці вправо, так що

\[g(x)=f(x−2) \nonumber\]

Зверніть увагу, як ми повинні ввести значення,$x=2$ щоб отримати вихідне значення$y=0$;$x$ значення -повинні бути на 2 одиниці більше через зсув вправо на 2 одиниці. Потім ми можемо використовувати визначення$f(x)$ функції, щоб написати формулу для$g(x)$ оцінки$f(x−2)$.

\[\begin{align*} f(x)&=x^2 \\ g(x)&=f(x-2) \\ g(x)&=f(x-2)=(x-2)^2 \end{align*}\]

Аналіз

Щоб визначити, чи є зсув$+2$ або$−2$, розглянемо одну точку відліку на графіку. Для квадратичного зручно дивитися на точку вершини. У вихідній функції,$f(0)=0$. У нашій зрушеній функції,$g(2)=0$. Для отримання вихідного значення 0 з функції нам потрібно вирішити$f$, чи буде працювати знак плюс або мінус для задоволення$g(2)=f(x−2)=f(0)=0$. Щоб це спрацювало, нам потрібно буде відняти 2 одиниці з наших вхідних значень.

Приклад$\PageIndex{7}$: Interpreting Horizontal versus Vertical Shifts

Функція$G(m)$ дає кількість галонів газу, необхідних для проїзду$m$ миль. Інтерпретувати$G(m)+10$ і$G(m+10)$

Рішення

$G(m)+10$можна інтерпретувати як додавання 10 до виходу, галонів. Це газ, необхідний для проїзду$m$ миль, плюс ще 10 галонів газу. Графік вказував би вертикальний зсув.

$G(m+10)$можна інтерпретувати як додавання 10 до входу, миль. Отже, це кількість галонів газу, необхідного для проїзду на 10 миль більше, ніж$m$ миль. Графік вказував би горизонтальний зсув.

Вправа$\PageIndex{7}$

Враховуючи функцію$f(x)=\sqrt{x}$, графуйте вихідну функцію$f(x)$ та перетворення$g(x)=f(x+2)$ на однакові осі. Це горизонтальний або вертикальний зсув? У який бік зсувається графік і на скільки одиниць?

Відповідь: Графіки$f(x)$ і$g(x)$ наведені нижче. Трансформація являє собою горизонтальний зсув. Функція зрушена вліво на 2 одиниці.

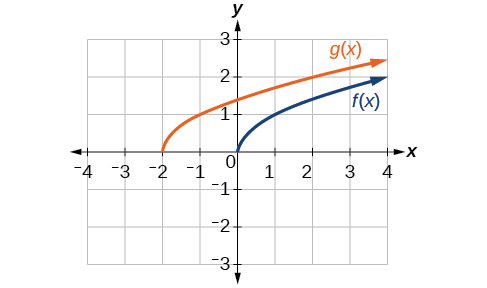
$Графік функції квадратного кореня та функції квадратного фута горизонтального зсуву.$
Малюнок$\PageIndex{8}$

Поєднання вертикальних і горизонтальних зсувів

Тепер, коли ми маємо дві трансформації, ми можемо об'єднати їх разом. Вертикальні зсуви - це зовнішні зміни, які впливають на значення вихідної$(y-)$ осі і зрушують функцію вгору або вниз. Горизонтальні зсуви - це зміни всередині, які впливають на значення вхідної$(x-)$ осі і зрушують функцію вліво або вправо. Поєднання двох типів зсувів призведе до зміни графіка функції вгору або вниз і вправо або вліво.

Як...

З огляду на функцію і вертикальний і горизонтальний зсув, намалюйте графік.

Визначте вертикальні і горизонтальні зсуви за формулою.
Вертикальний зсув є результатом константи, доданої до виводу. Перемістіть графік вгору для позитивної константи і вниз для негативної константи.
Горизонтальний зсув виникає з константи, доданої до вхідних даних. Перемістіть графік вліво для позитивної константи і вправо для негативної константи.
Застосовуйте зрушення до графіка в будь-якому порядку.

Приклад$\PageIndex{8}$: Graphing Combined Vertical and Horizontal Shifts

Дано$f(x)=|x|$, накидаємо графік$h(x)=f(x+1)−3$.

Рішення

Функція$f$ є нашим інструментарієм функції абсолютного значення. Ми знаємо, що цей графік має форму V, з точкою в початку. Графік$h$ трансформувався двома$f$ способами:$f(x+1)$ це зміна на внутрішній стороні функції, що дає горизонтальний зсув вліво на 1, а віднімання на 3 в$f(x+1)−3$ - це зміна зовнішньої частини функції, що дає вертикальний зсув вниз на 3. Трансформація графіка проілюстрована на рисунку$\PageIndex{9}$.

Простежимо за однією точкою графіка$f(x)=|x|$.

Точка$(0,0)$ трансформується спочатку зміщенням вліво на 1 одиницю:$(0,0)\rightarrow(−1,0)$
Точка$(−1,0)$ трансформується далі, зміщуючи вниз 3 одиниці:$(−1,0)\rightarrow(−1,−3)$

Графік абсолютної функції, <span translate= — Малюнок$\PageIndex{9}$: Графік абсолютної функції$y=|x|$, і як вона була перетворена в$y=|x+1|-3$

На малюнку$\PageIndex{10}$ показаний графік$h$.

Кінцева функція <span translate= — Малюнок$\PageIndex{10}$: Кінцева функція$y=|x+1|-3$.

Вправа$\PageIndex{8}$

Дано$f(x)=|x|$, накидаємо графік$h(x)=f(x−2)+4$.

Відповідь: $альт$
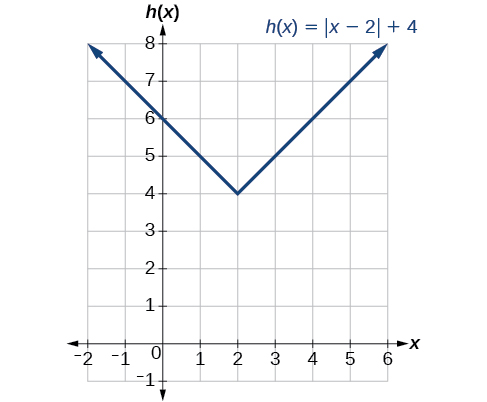
Малюнок$\PageIndex{11}$

Приклад$\PageIndex{9}$: Identifying Combined Vertical and Horizontal Shifts

Напишіть формулу для графіка, показаного на малюнку$\PageIndex{12}$, який є перетворенням інструментарію функції квадратного кореня.

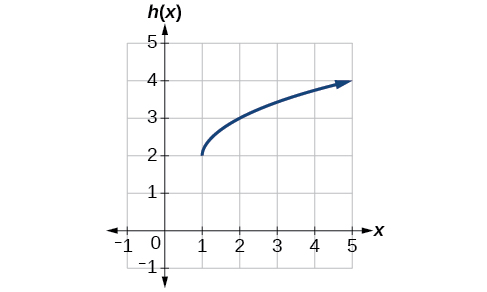
Графік функції квадратного кореня транспонований праворуч на одиницю і вгору 2. — Малюнок$\PageIndex{12}$: Графік функції квадратного кореня, перенесеної праворуч на одиницю і вгору 2.

Рішення

Графік функції інструментарію починається з початку, тому цей графік був зміщений на 1 вправо і вгору на 2. У функції позначення, ми могли б написати, що як

\[h(x)=f(x−1)+2 \nonumber\]

Використовуючи формулу для функції квадратного кореня, ми можемо записати

\[h(x)=\sqrt{x−1}+2 \nonumber\]

Аналіз

Зверніть увагу, що це перетворення змінило область і діапазон функції. Цей новий граф має домен$\left[1,\infty\right)$ і діапазон$\left[2,\infty\right)$.

Вправа$\PageIndex{9}$

Напишіть формулу перетворення реципрокної функції інструментарію$f(x)=\frac{1}{x}$, яка зміщує графік функції на одну одиницю вправо і на одну одиницю вгору.

Відповідь: \[g(x)=\dfrac{1}{x-1}+1 \nonumber \]

Графічні функції з використанням роздумів про осі

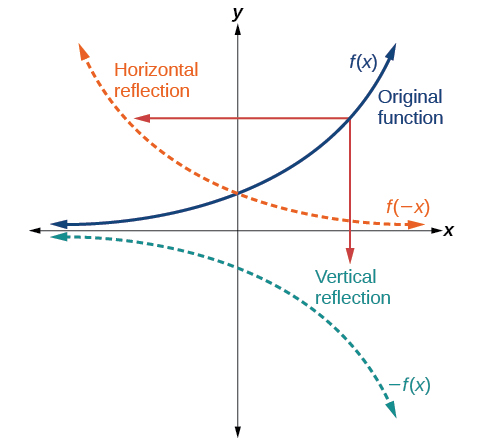
Іншим перетворенням, яке можна застосувати до функції, є відображення над віссю x або y. Вертикальне відображення відображає графік вертикально по осі x, тоді як горизонтальне відображення відображає графік горизонтально по осі Y. Відбиття наведені на рис$\PageIndex{13}$.

Рисунок$\PageIndex{13}$: Графік вертикального та горизонтального відображення функції.

Зверніть увагу, що вертикальне відображення створює новий графік, який є дзеркальним відображенням базового або вихідного графіка навколо осі x. Горизонтальне відображення створює новий графік, який є дзеркальним відображенням базового або вихідного графіка навколо осі y.

Визначення: Роздуми

З огляду на функцію$f(x)$, нова функція$g(x)=−f(x)$ є вертикальним відображенням функції$f(x)$, іноді називається відображенням про (або над, або через) вісь x.

З огляду на функцію$f(x)$, нова функція$g(x)=f(−x)$ - це горизонтальне відображення функції$f(x)$, яке іноді називають відображенням навколо осі y.

Як...

Задано функцію, відображають графік як вертикально, так і по горизонталі.

Помножте всі виходи на —1 для вертикального відображення. Новий графік є відображенням вихідного графіка навколо осі x.
Помножте всі вхідні дані на —1 для горизонтального відображення. Новий графік є відображенням вихідного графіка навколо осі y.

Приклад$\PageIndex{10}$: Reflecting a Graph Horizontally and Vertically

Відобразіть графік$s(t)=\sqrt{t}$ (а) вертикально і (b) по горизонталі.

Рішення

a Відображення графіка по вертикалі означає, що кожне вихідне значення буде відображено над горизонтальною віссю t, як показано на малюнку$\PageIndex{14}$.

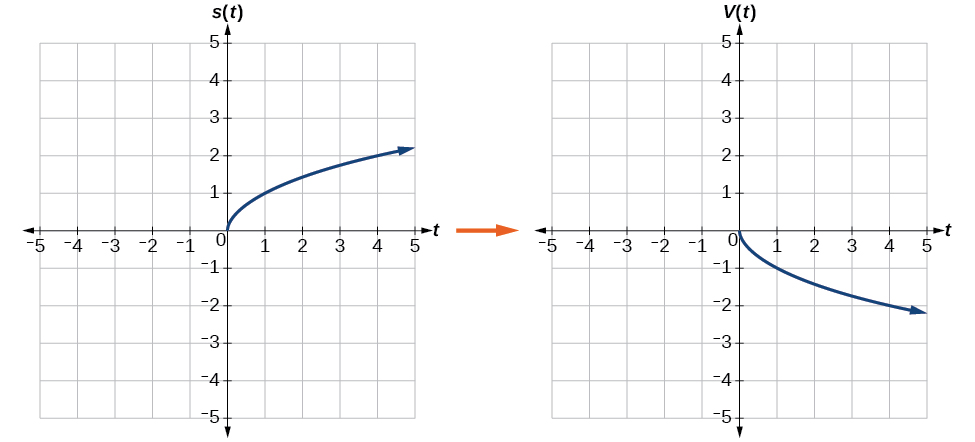
Рисунок$\PageIndex{14}$: Графік вертикального відображення функції квадратного кореня.

Оскільки кожне вихідне значення протилежне вихідному значенню, ми можемо записати

\[V(t)=−s(t) \text{ or } V(t)=−\sqrt{t} \nonumber\]

Зверніть увагу, що це зовнішня зміна, або вертикальний зсув, що впливає на вихідні$s(t)$ значення, тому негативний знак належить поза функцією.

b Відображення по горизонталі означає, що кожне вхідне значення буде відображатися над вертикальною віссю, як показано на малюнку$\PageIndex{15}$.

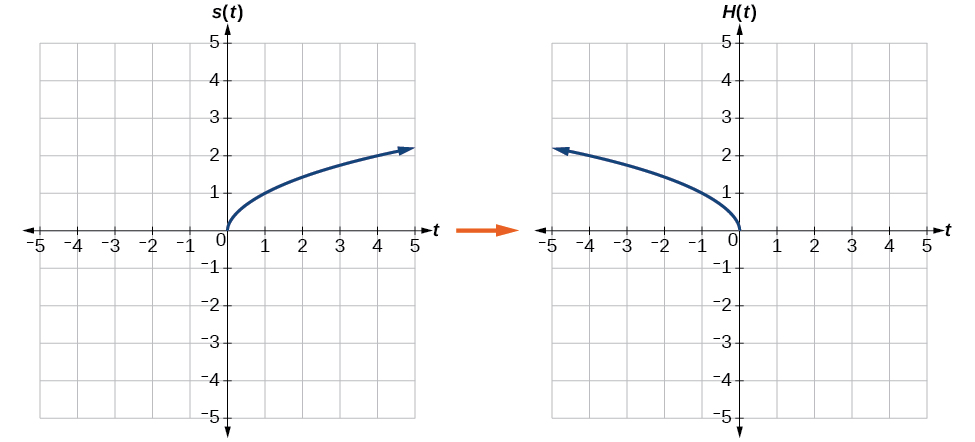
Графік горизонтального відображення функції квадратного кореня. — Малюнок$\PageIndex{15}$: Горизонтальне відображення функції квадратного кореня

Оскільки кожне вхідне значення протилежне вихідному вхідному значенню, ми можемо написати

\[H(t)=s(−t) \text{ or } H(t)=\sqrt{−t} \nonumber\]

Зверніть увагу, що це внутрішня зміна або горизонтальна зміна, яка впливає на вхідні значення, тому негативний знак знаходиться всередині функції.

Зверніть увагу, що ці перетворення можуть впливати на область і діапазон функцій. Хоча оригінальна функція квадратного кореня має область$\left[0,\infty\right)$ і діапазон$\left[0,\infty\right)$, вертикальне відображення дає$V(t)$ функції діапазон,$\left(−\infty,0\right]$ а горизонтальне відображення дає$H(t)$ функцію області$\left(−\infty, 0\right]$.

Вправа$\PageIndex{5}$

Відобразіть графік$f(x)=|x−1|$ (а) вертикально і (b) по горизонталі.

Відповідь

а.

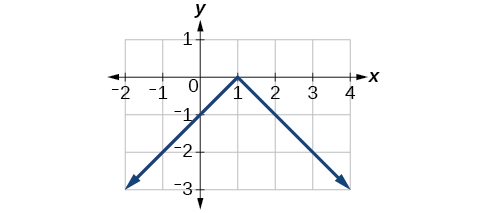
Рисунок$\PageIndex{16}$: Графік вертикально відображеної абсолютної функції.

б.

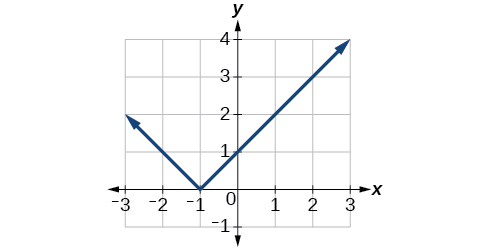
Рисунок$\PageIndex{17}$: Графік абсолютної функції перекладено на одну одиницю ліворуч.

Приклад$\PageIndex{11}$: Reflecting a Tabular Function Horizontally and Vertically

Функція$f(x)$ задається як Таблиця$\PageIndex{6}$. Створіть таблицю для функцій нижче.

а.$g(x)=−f(x)$
б.$h(x)=f(−x)$

Таблиця$\PageIndex{6}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

а Для$g(x)$, негативний знак поза функцією вказує на вертикальне відображення, тому значення x залишаються однаковими, і кожне вихідне значення буде протилежним вихідному значенню. Див$\PageIndex{7}$. Таблицю.

Таблиця$\PageIndex{7}$
$x$	2	4	6	8
$g(x)$	-1	-3	-7	-11

б Для$h(x)$, негативний знак всередині функції вказує на горизонтальне відображення, тому кожне вхідне значення буде протилежним початковому вхідному значенню, а$h(x)$ значення залишаються такими ж, як і$f(x)$ значення. Див$\PageIndex{8}$. Таблицю.

Таблиця$\PageIndex{8}$
$x$	-2	-4	-6	-8
$h(x)$	1	3	7	11

Вправа$\PageIndex{6}$

Функція$f(x)$ задається як Таблиця$\PageIndex{9}$. Створіть таблицю для функцій нижче.

а.$g(x)=−f(x)$
б.$h(x)=f(−x)$

Таблиця$\PageIndex{9}$
$x$	-2	0	2	4
$f(x)$	5	10	15	20

Відповідь

а.$g(x)=−f(x)$

Таблиця$\PageIndex{10}$
$x$	-2	0	2	4
$g(x)$	-5	-10	-15	-20

б.$h(x)=f(−x)$

Таблиця$\PageIndex{11}$
$x$	-2	0	2	-4
$h(x)$	15	10	5	20

Приклад$\PageIndex{12}$: Applying a Learning Model Equation

Загальна модель навчання має рівняння,$k$ подібне до$k(t)=−2^{−t}+1$, де відсоток майстерності, який може бути досягнутий після$t$ практичних занять. Це перетворення функції,$f(t)=2^t$ показаної на рис$\PageIndex{18}$. Намалюйте графік$k(t)$.

Графік перекладу <span = — Малюнок$\PageIndex{18}$: Графік$k(t)$

Рішення

Це рівняння об'єднує три перетворення в одне рівняння.

Горизонтальне відображення:$f(−t)=2^{−t}$
Вертикальне відображення:$−f(−t)=−2^{−t}$
Вертикальний зсув:$−f(−t)+1=−2^{−t}+1$

Ми можемо намалювати графік, застосовуючи ці перетворення по одному до вихідної функції. Давайте простежимо два пункти через кожну з трьох перетворень. Ми виберемо точки$(0, 1)$ і$(1, 2)$.

Спочатку застосовуємо горизонтальне відображення:$(0, 1) \; (–1, 2)$.
Потім наносимо вертикальне відображення:$(0, −1) \; (-1, –2)$.
Нарешті, застосовуємо вертикальний зсув:$(0, 0) \; (-1, -1)$.

Це означає, що початкові точки,$(0,1)$ і$(1,2)$ стають$(0,0)$ і$(-1,-1)$ після того, як ми застосовуємо перетворення.

На$\PageIndex{19}$ малюнку перший графік виходить з горизонтального відображення. Друге є результатом вертикального відображення. Третій виходить від вертикального зсуву вгору на 1 одиницю.

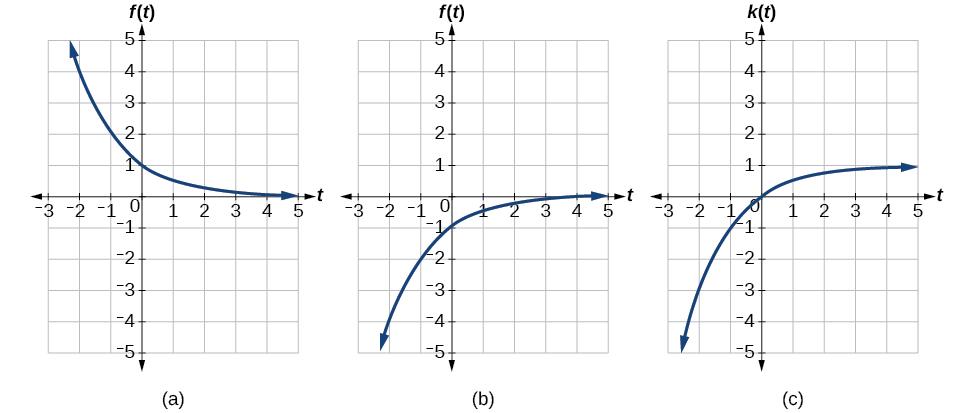
Малюнок$\PageIndex{19}$: Графіки всіх перетворень.

Аналіз

Як модель для навчання, ця функція буде обмежена областю$t\geq0$, з відповідним діапазоном$\left[0,1\right)$.

Вправа$\PageIndex{7}$

Дано функцію інструментарію$f(x)=x^2$, граф$g(x)=−f(x)$ і$h(x)=f(−x)$. Зверніть увагу на будь-яку дивовижну поведінку цих функцій.

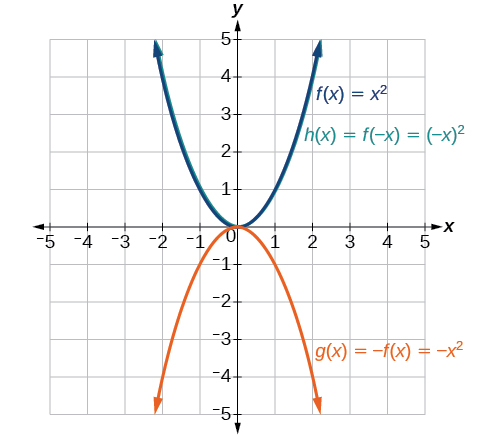
Відповідь: $Графік x^2 та його відображення.$
Малюнок$\PageIndex{20}$: Графік$x^2$ і його відображення.

Зверніть увагу:$g(x)=f(−x)$ виглядає так само, як$f(x)$.

Визначення парних і непарних функцій

Деякі функції проявляють симетрію, так що відображення призводять до вихідного графіка. Наприклад, горизонтально відображаючи функції інструментарію$f(x)=x^2$ або$f(x)=|x|$ призведе до вихідного графіка. Ми говоримо, що ці типи графіків симетричні щодо осі y. Функції, графіки яких симетричні щодо осі y, називаються парними функціями.

Якби графіки$f(x)=x^3$ або$f(x)=\frac{1}{x}$ були відображені над обома осями, результатом буде вихідний графік, як показано на малюнку$\PageIndex{21}$.

Ми говоримо, що ці графіки симетричні щодо походження. Функція з графом, симетричним щодо походження, називається непарною функцією.

Примітка: Функція не може бути ні парною, ні непарною, якщо вона не проявляє жодної симетрії. Наприклад, не$f(x)=2^x$ є ні парним, ні непарним. Також єдиною функцією, яка є і парною, і непарною, є постійна функція$f(x)=0$.

Визначення: парні та непарні функції

Функція називається парною функцією, якщо для кожного входу$x$

$f(x)=f(−x)$

Графік парної функції симетричний щодо осі y.

Функція називається непарною функцією, якщо для кожного входу$x$

$f(x)=−f(−x)$

Графік непарної функції симетричний щодо походження.

Як...

Задано формулу для функції, визначте, чи є функція парною, непарною чи ні.

Визначте, чи задовольняє функція$f(x)=f(−x)$. Якщо це так, то навіть.
Визначте, чи задовольняє функція$f(x)=−f(−x)$. Якщо це так, це непарно.
Якщо функція не задовольняє жодному правилу, вона не парна і не непарна.

Приклад$\PageIndex{13}$: Determining whether a Function Is Even, Odd, or Neither

Функція$f(x)=x^3+2x$ парна, непарна чи ні?

Рішення

Не дивлячись на графік, ми можемо визначити, чи функція парна чи непарна, знайшовши формули для відображень та визначаючи, чи повертають вони нас до вихідної функції. Почнемо з правила для парних функцій.

\[f(−x)=(−x)^3+2(−x)=−x^3−2x \nonumber\]

Це не повертає нас до початкової функції, тому ця функція навіть не є. Тепер ми можемо перевірити правило для непарних функцій.

\[−f(−x)=−(−x^3−2x)=x^3+2x \nonumber\]

Тому що$−f(−x)=f(x)$, це непарна функція.

Аналіз

Розглянемо графік$f$ на рис$\PageIndex{22}$. Зверніть увагу, що графік симетричний щодо походження. Для кожної точки$(x,y)$ на графіку відповідна точка також$(−x,−y)$ знаходиться на графіку. Наприклад,$(1, 3)$ знаходиться на графіку$f$, а відповідна точка також$(−1,−3)$ знаходиться на графіку.

Вправа$\PageIndex{8}$

Функція$f(s)=s^4+3s^2+7$ парна, непарна чи ні?

Відповідь: навіть

Графічні функції з використанням розтяжок і стиснень

Додавання константи до входів або виходів функції змінювало положення графіка щодо осей, але це не вплинуло на форму графіка. Тепер ми досліджуємо ефекти множення входів або виходів на деяку кількість.

Ми можемо перетворити всередині (вхідні значення) функції або ми можемо перетворити зовнішні (вихідні значення) функції. Кожна зміна має певний ефект, який можна побачити графічно.

Вертикальні розтяжки і стиснення

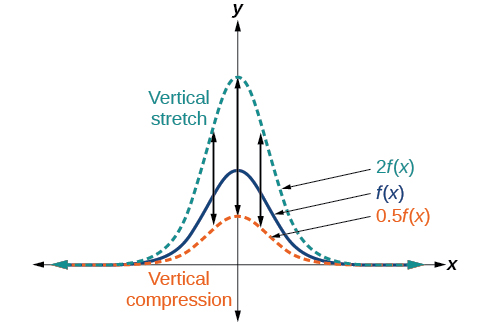
Коли ми множимо функцію на позитивну константу, ми отримуємо функцію, графік якої розтягнутий або стиснутий вертикально по відношенню до графіка вихідної функції. Якщо константа більше 1, ми отримуємо вертикальне розтягнення; якщо константа знаходиться в межах від 0 до 1, отримуємо вертикальне стиснення. $\PageIndex{23}$На малюнку показана функція, помножена на постійні коефіцієнти 2 і 0,5 і отримані вертикальні розтягування і стиснення.

Графік функції, яка показує вертикальне розтягування та стиснення. — Малюнок$\PageIndex{23}$: Вертикальне розтягування і стиснення

Визначення: Вертикальні розтяжки та стиснення

З огляду на функцію$f(x)$, нова функція$g(x)=af(x)$, де$a$ константа, є вертикальним розтягуванням або вертикальним стисненням функції$f(x)$.

Якщо$a>1$, то графік буде розтягнутий.
Якщо$0<a<1$, то графік буде стиснутий.
Якщо$a<0$, то буде поєднання вертикальної розтяжки або стиснення з вертикальним відображенням.

Як...

Дано функцію, графік її вертикального розтягування.

Визначте значення$a$.
Помножити всі значення діапазону на$a$
Якщо$a>1$, графік розтягується на коефіцієнт$a$.
Якщо$0<a<1$, графік стискається в коефіцієнт$a$.
Якщо$a<0$, графік або розтягується, або стискається, а також відбивається про вісь x.

Приклад 1.5.14: Графік вертикального розтягування

Функція$P(t)$ моделює популяцію дрозофіл. Графік наведено на малюнку$\PageIndex{24}$.

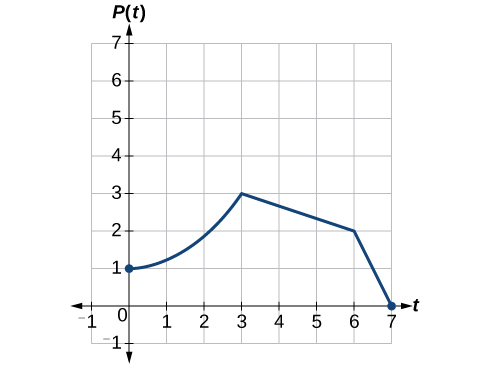
Малюнок$\PageIndex{24}$: Графік для представлення зростання популяції дрозофіл.

Вчений порівнює цю популяцію з іншою популяцією$Q$, зростання якої йде за тією ж схемою, але в два рази більше. Намалюйте графік цієї сукупності.

Рішення

Оскільки кількість населення завжди вдвічі більша, вихідні значення нової популяції завжди вдвічі перевищують вихідні значення вихідної функції. Графічно це показано на малюнку$\PageIndex{25}$.

Якщо ми виберемо чотири опорні точки$(0, 1)$,$(3, 3)$,,$(6, 2)$ і$(7, 0)$ ми помножимо всі виходи на 2.

Нижче показано, де будуть розташовані нові точки для нового графіка.

\[(0, 1)\rightarrow(0, 2)\]

\[(3, 3)\rightarrow(3, 6)\]

\[(6, 2)\rightarrow(6, 4)\]

\[(7, 0)\rightarrow(7, 0)\]

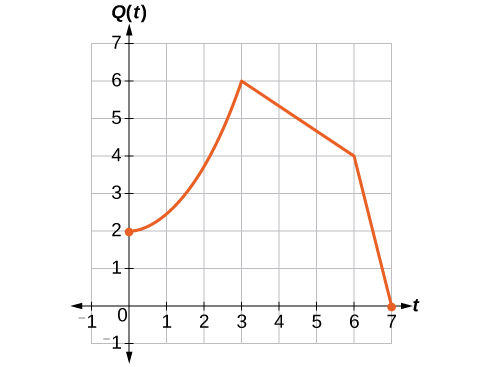
Графік функції популяції подвоївся. — Малюнок$\PageIndex{25}$: Графік функції популяції подвоюється.

Символічно відносини пишуться як

\[Q(t)=2P(t) \nonumber\]

Це означає$t$, що для будь-якого входу значення функції$Q$ в два рази перевищує значення функції$P$. Зверніть увагу, що ефект на графіку є вертикальним розтягуванням графіка, де кожна точка подвоює свою відстань від горизонтальної осі. Вхідні значення залишаються незмінними$t$, а вихідні значення вдвічі більші, ніж раніше.

Як...

З огляду на табличну функцію і припускаючи, що перетворення є вертикальним розтягуванням або стисненням, створіть таблицю для вертикального стиснення.

Визначте значення$a$.
Помножте всі вихідні значення на$a$.

Приклад$\PageIndex{15}$: Finding a Vertical Compression of a Tabular Function

Функція$f$ задається як Таблиця$\PageIndex{12}$. Створіть таблицю для функції$g(x)=\frac{1}{2}f(x)$.

Таблиця$\PageIndex{12}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

Рішення

Формула$g(x)=\frac{1}{2}f(x)$ говорить нам, що вихідні значення$g$ є половиною вихідних значень$f$ з однаковими входами. Наприклад, ми це знаємо$f(4)=3$. Тоді

\[g(4)=\frac{1}{2}f(4)=\frac{1}{2}(3)=\frac{3}{2} \nonumber\]

Ми робимо те ж саме для інших значень, щоб створити таблицю$\PageIndex{13}$.

Таблиця$\PageIndex{13}$
$x$	2	4	6	8
$g(x)$	$\dfrac{1}{2}$	$\dfrac{3}{2}$	$\dfrac{7}{2}$	$\dfrac{11}{2}$

Аналіз

Результатом є те, що функція$g(x)$ була стиснута вертикально$\frac{1}{2}$. Кожне вихідне значення ділиться навпіл, тому графік дорівнює половині початкової висоти.

Вправа$\PageIndex{9}$

Функція$f$ задається як Таблиця$\PageIndex{14}$. Створіть таблицю для функції$g(x)=\frac{3}{4}f(x)$.

Таблиця$\PageIndex{14}$
$x$	2	4	6	8
$f(x)$	12	16	20	0

Відповідь

Таблиця$\PageIndex{15}$
$x$	2	4	6	8
$g(x)$	9	12	15	0

Приклад$\PageIndex{16}$: Recognizing a Vertical Stretch

Графік на малюнку$\PageIndex{26}$ є перетворенням функції інструментарію$f(x)=x^3$. Пов'язати цю нову функцію$g(x)$$f(x)$, а потім знайти формулу для$g(x)$.

[Графік перетворення <span translate= — Малюнок$\PageIndex{26}$: Графік перетворення$f(x)=x^3$

При спробі визначити вертикальний розтяг або зсув корисно шукати точку на графіку, яка є відносно чіткою. На цьому графіку, здається, що$g(2)=2$. З основною кубічною функцією на одному вході,$f(2)=2^3=8$. Виходячи з цього, виявляється, що виходи$g$ є$\frac{1}{4}$ виходами функції,$f$ тому що$g(2)=\frac{1}{4}f(2)$. З цього можна досить сміливо зробити висновок, що$g(x)=\frac{1}{4}f(x)$.

Ми можемо написати$g$ формулу для, використовуючи визначення функції$f$.

\[g(x)=\frac{1}{4} f(x)=\frac{1}{4}x^3.\]

Вправа$\PageIndex{1}$

Запишіть формулу для функції, яку ми отримуємо, коли розтягуємо функцію інструментарію ідентичності на коефіцієнт 3, а потім зрушуємо її вниз на 2 одиниці.

Відповідь: $g(x)=3x-2$

Горизонтальні розтяжки і стиснення

Тепер ми розглянемо зміни всередині функції. Коли ми множимо вхід функції на позитивну константу, ми отримуємо функцію, графік якої розтягується або стискається горизонтально по відношенню до графіка вихідної функції. Якщо константа знаходиться в межах від 0 до 1, ми отримуємо горизонтальне розтягнення; якщо константа більше 1, отримуємо горизонтальне стиснення функції.

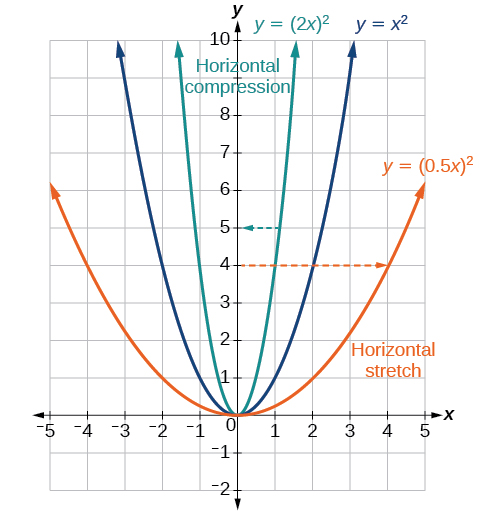
Графік вертикального розтягування та стиснення x^2. — Малюнок$\PageIndex{27}$: Графік вертикального розтягування і стиснення$x^2$.

З огляду на функцію$y=f(x)$, форма$y=f(bx)$ призводить до горизонтального розтягування або стиснення. Розглянемо функцію$y=x^2$. Дотримуйтесь Малюнок$\PageIndex{27}$. Графік$y=(0.5x)^2$ - горизонтальне розтягнення графіка функції$y=x^2$ в 2 рази. Графік$y=(2x)^2$ - це горизонтальне стиснення графіка функції$y=x^2$ в 2 рази.

Визначення: Горизонтальні розтяжки та стиснення

З огляду на функцію$f(x)$, нова функція$g(x)=f(bx)$, де$b$ константа, є горизонтальним розтягуванням або горизонтальним стисненням функції$f(x)$.

Якщо$b>1$, то графік буде стиснутий$\frac{1}{b}$.
Якщо$0<b<1$, то графік буде розтягнутий на$\frac{1}{b}$.
Якщо$b<0$, то буде поєднання горизонтального розтягування або стиснення з горизонтальним відображенням.

Як...

Давши опис функції, намалюйте горизонтальне стиснення або розтягування.

Напишіть формулу для представлення функції.
Встановіть$g(x)=f(bx)$ де$b>1$ для стиснення або$0<b<1$ для розтяжки.

Приклад$\PageIndex{17}$: Graphing a Horizontal Compression

Припустимо, вчений порівнює популяцію плодових мух з популяцією, яка прогресує протягом свого життя вдвічі швидше, ніж початкова популяція. Іншими словами, ця нова популяція буде прогресувати за 1 годину стільки ж$R$, скільки це робить вихідне населення за 2 години, а через 2 години воно буде прогресувати стільки, скільки це робить вихідне населення за 4 години. Намалюйте графік цієї сукупності.

Рішення

Символічно, ми могли б написати

$\begin{align} R(1)&=P(2), \\ R(2)&=P(4), &\text{and in general,} \\ R(t)&=P(2t).\end{align}$

Див. Рисунок$\PageIndex{28}$ для графічного порівняння вихідної сукупності та стисненої популяції.

Два пліч-о-пліч графіки. Перший граф має функцію для вихідної сукупності, область якої [0,7] і діапазон [0,3]. Максимальне значення відбувається при (3,3). Другий графік має таку ж форму, як і перший, за винятком того, що він вдвічі менше ширини. Це графік трансформованої сукупності, з доменом [0, 3,5] і діапазоном [0,3]. Максимум припадає на (1,5, 3). — Рисунок$\PageIndex{28}$: (a) Оригінальний графік популяції (b) Стиснутий графік популяції

Аналіз

Зауважте, що ефект на графіку є горизонтальним стисненням, де всі вхідні значення складають половину початкової відстані від вертикальної осі.

Приклад$\PageIndex{18}$: Finding a Horizontal Stretch for a Tabular Function

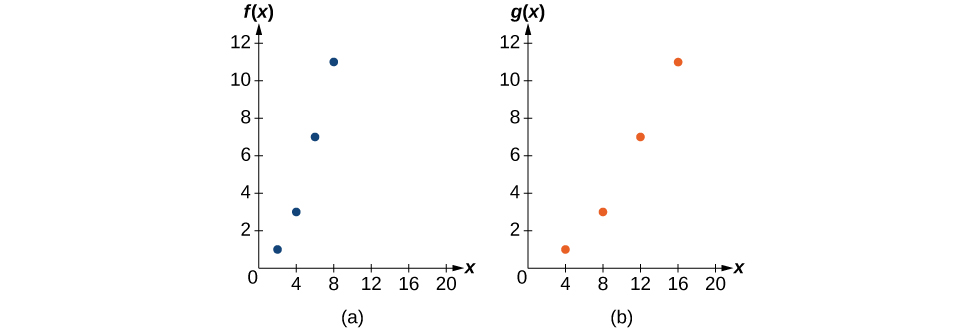
Функція$f(x)$ задається як Таблиця$\PageIndex{16}$. Створіть таблицю для функції$g(x)=f(\frac{1}{2}x)$.

Таблиця$\PageIndex{16}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

Формула$g(x)=f(\frac{1}{2}x)$ говорить нам, що вихідні значення для$g$ збігаються з вихідними значеннями для функції$f$ на вході в половину розміру. Зверніть увагу, що у нас недостатньо інформації, щоб визначити$g(2)$ тому$g(2)=f(\frac{1}{2}⋅2)=f(1)$, що, і ми не маємо значення для$f(1)$ нашої таблиці. Наші вхідні значення повинні бути в два рази більше, щоб отримати вхідні дані для$f$ того, що ми можемо оцінити.$g$ Наприклад, ми можемо визначити$g(4)$.

\[g(4)=f(\dfrac{1}{2}⋅4)=f(2)=1\]

Ми робимо те ж саме для інших значень, щоб створити таблицю$\PageIndex{17}$.

Таблиця$\PageIndex{17}$
$x$	4	8	12	16
$g(x)$	1	3	7	11

$\PageIndex{29}$На малюнку показані графіки обох цих наборів точок.

Малюнок$\PageIndex{29}$: Графік попередньої таблиці.

Аналіз

Оскільки кожне вхідне значення було подвоєно, результатом є те, що функція$g(x)$ була розтягнута горизонтально в 2 рази.

Приклад$\PageIndex{19}$: Recognizing a Horizontal Compression on a Graph

$g(x)$Пов'язати функцію з$f(x)$ малюнком$\PageIndex{30}$.

Рішення

Графік$g(x)$ виглядає як графік$f(x)$ горизонтально стиснутого. Оскільки$f(x)$ закінчується на (6,4) і$g(x)$ закінчується на (2,4), ми можемо бачити, що значення x були стиснуті$\frac{1}{3}$, тому що$6(\frac{1}{3})=2$. Ми також можемо помітити, що$g(2)=f(6)$ і$g(1)=f(3)$. У будь-якому випадку, ми можемо описати ці відносини як$g(x)=f(3x)$. Це горизонтальне стиснення по$\frac{1}{3}$.

Аналіз

Зверніть увагу, що коефіцієнт, необхідний для горизонтального розтягування або стиснення, є зворотним розтягування або стиснення. Отже, щоб розтягнути графік по горизонталі на коефіцієнт масштабу 4, нам потрібен коефіцієнт$\frac{1}{4}$ в нашій функції:$f(\frac{1}{4}x)$. Це означає, що вхідні значення повинні бути в чотири рази більше, щоб отримати той самий результат, вимагаючи, щоб вхід був більшим, викликаючи горизонтальне розтягування.

Вправа$\PageIndex{11}$

Напишіть формулу для інструментарію функції квадратного кореня горизонтально розтягнутої в 3 рази.

Відповідь: $g(x)=f(\frac{1}{3}x)$, Таким чином, використовуючи функцію квадратного кореня ми отримуємо$g(x)=\sqrt{\frac{1}{3}x}$

Виконання послідовності перетворень

При комбінуванні перетворень дуже важливо враховувати порядок перетворень. Наприклад, вертикальне зсув на 3, а потім вертикально розтягування на 2 не створює такий же графік, як вертикальне розтягування на 2, а потім вертикально зсувається на 3, тому що коли ми спочатку зрушуємо, і вихідна функція, і зрушення розтягуються, тоді як тільки вихідна функція розтягується, коли ми спочатку розтягуємо.

Коли ми бачимо такий вираз$2f(x)+3$, як, з якої трансформації ми повинні почати? Відповідь тут випливає красиво з порядку операцій. З огляду на вихідне значення$f(x)$, ми спочатку множимо на 2, викликаючи вертикальне розтягування, а потім додаємо 3, викликаючи вертикальний зсув. Іншими словами, множення перед додаванням.

Горизонтальні перетворення трохи складніше думати. Коли ми пишемо$g(x)=f(2x+3)$, наприклад, ми повинні думати про те, як входи до функції$g$ відносяться до входів до функції$f$. Припустимо, ми знаємо$f(7)=12$. Який вхід$g$ буде виробляти цей вихід? Іншими словами, яке значення$x$ дозволить$g(x)=f(2x+3)=12?$ нам знадобиться$2x+3=7$. Щоб вирішити для$x$, ми спочатку віднімаємо 3, в результаті чого горизонтальний зсув, а потім ділимо на 2, викликаючи горизонтальне стиснення.

Цей формат в кінцевому підсумку дуже важко працювати, оскільки зазвичай набагато простіше горизонтально розтягнути графік перед зміщенням. Ми можемо обійти це шляхом факторингу всередині функції.

\[f(bx+p)=f(b(x+\frac{p}{b})) \nonumber\]

Давайте попрацюємо на прикладі.

\[f(x)=(2x+4)^2 \nonumber\]

Ми можемо врахувати 2.

\[f(x)=(2(x+2))^2 \nonumber\]

Тепер ми можемо більш чітко спостерігати горизонтальний зсув вліво на 2 одиниці і горизонтальне стиснення. Факторинг таким чином дозволяє спочатку горизонтально розтягуватися, а потім зсуватися по горизонталі.

Поєднання перетворень

При об'єднанні вертикальних перетворень, написаних у формі$af(x)+k$, спочатку вертикально розтягують на,$a$ а потім по вертикалі зрушують на$k$.
При комбінуванні горизонтальних перетворень, написаних у формі$f(bx+h)$, спочатку горизонтально зрушують на,$h$ а потім горизонтально розтягують на$\frac{1}{b}$.
При комбінуванні горизонтальних перетворень, написаних у формі$f(b(x+h))$, спочатку горизонтально розтягують на,$\frac{1}{b}$ а потім горизонтально зрушують на$h$.
Горизонтальні і вертикальні перетворення незалежні. Неважливо, горизонтальні або вертикальні перетворення виконуються першими.

Приклад$\PageIndex{20}$: Finding a Triple Transformation of a Tabular Function

Дано таблицю$\PageIndex{18}$ для функції$f(x)$, створіть таблицю значень функції$g(x)=2f(3x)+1$.

Таблиця$\PageIndex{18}$
$x$	6	12	18	24
$f(x)$	10	14	15	17

Рішення

Є три кроки до цього перетворення, і ми будемо працювати зсередини назовні. Починаючи з горизонтальних перетворень,$f(3x)$ це горизонтальне стиснення на$\frac{1}{3}$, що означає множимо кожне$x$ -значення на$\frac{1}{3}$ .Див$\PageIndex{19}$. Таблицю.

Таблиця$\PageIndex{19}$
$x$	2	4	6	8
$f(3x)$	10	14	15	17

Дивлячись тепер до вертикальних перетворень, почнемо з вертикальної розтяжки, яка помножить вихідні значення на 2. Застосовуємо це до попереднього перетворення. Див$\PageIndex{20}$. Таблицю.

Таблиця$\PageIndex{20}$
$x$	2	4	6	8
$2f(3x)$	20	28	30	34

Нарешті, ми можемо застосувати вертикальний зсув, який додасть 1 до всіх вихідних значень. Див$\PageIndex{21}$. Таблицю.

Таблиця$\PageIndex{21}$
$x$	2	4	6	8
$g(x)=2f(3x)+1+1$	21	29	31	35

Приклад$\PageIndex{21}$: Finding a Triple Transformation of a Graph

Використовуйте графік на$f(x)$ малюнку$\PageIndex{31}$ для ескізу графіка$k(x)=f\Big(\frac{1}{2}x+1\Big)−3$.

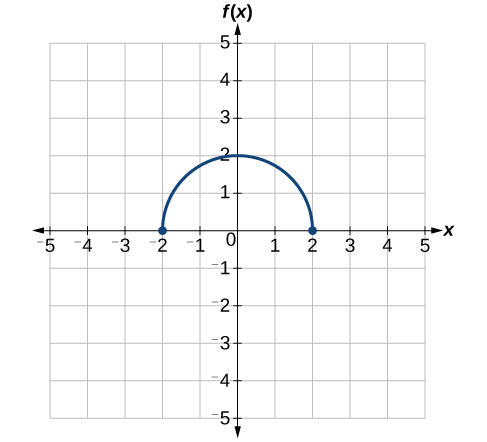
Малюнок$\PageIndex{31}$: Графік півкола.

Щоб спростити, давайте почнемо з факторингу всередині функції.

\[f\Big(\dfrac{1}{2}x+1\Big)−3=f\Big(\dfrac{1}{2}(x+2)\Big)−3\]

Враховуючи внутрішню частину, ми можемо спочатку горизонтально розтягнути на 2, як$\frac{1}{2}$ зазначено на внутрішній стороні функції. Пам'ятайте, що подвійний розмір 0 все ще дорівнює 0, тому точка$(0,2)$ залишається в той$(0,2)$ час як точка$(2,0)$ буде розтягуватися до$(4,0)$. Див$\PageIndex{32}$. Малюнок.

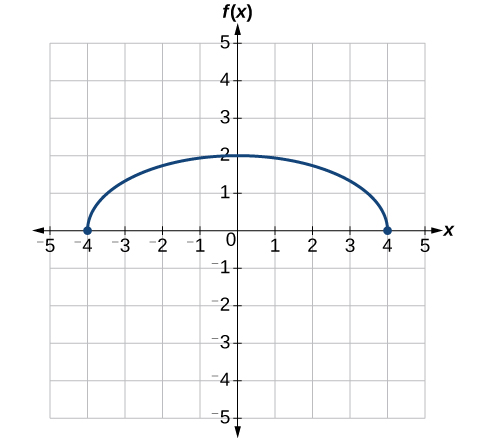
Далі горизонтально зрушуємо вліво на 2 одиниці, як зазначено$x+2$. Див$\PageIndex{33}$. Малюнок.

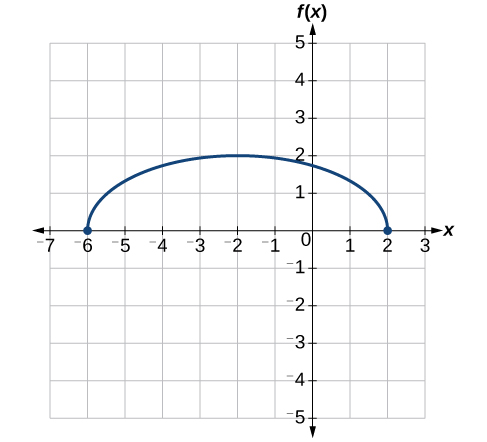
Нарешті, ми вертикально зрушуємо вниз на 3, щоб завершити наш ескіз, як вказує −3 на зовнішній стороні функції. Див$\PageIndex{34}$. Малюнок.

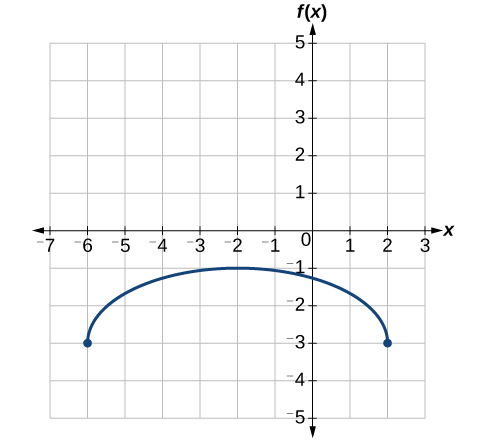
Ключові рівняння

Вертикальний зсув$g(x)=f(x)+k$ (вгору для$k>0$)
Горизонтальний зсув$g(x)=f(x−h)$ (праворуч) для$h>0$
Вертикальне відображення$g(x)=−f(x)$
Горизонтальне відображення$g(x)=f(−x)$
Вертикальна розтяжка$g(x)=af(x)$ (a> 0)
Вертикальне стиснення$g(x)=af(x)$ (0 <a<1)
горизонтальна розтяжка$g(x)=f(bx)(0<b<1)$
Горизонтальне стиснення$g(x)=f(bx)$ (b> 1)

Ключові концепції

Функцію можна зсунути вертикально, додавши константу до виводу.
Функція може бути зрушена горизонтально шляхом додавання константи до вхідних даних.
Пов'язка зсуву з контекстом задачі дає можливість порівнювати та інтерпретувати вертикальні та горизонтальні зсуви.
Вертикальні і горизонтальні зсуви часто поєднуються.
Вертикальне відображення відображає графік навколо осі x. Графік можна відобразити вертикально, множивши результат на —1.
Горизонтальне відображення відображає графік навколо осі y. Графік можна відобразити горизонтально, множивши вхідні дані на —1.
Графік може відображатися як вертикально, так і горизонтально. Порядок, в якому застосовуються відбиття, не впливає на остаточний графік.
Функція, представлена в табличній формі, також може бути відображена шляхом перемноження значень у вхідних і вихідних рядках або стовпцях відповідно.
Функцію, представлену у вигляді рівняння, можна відобразити, застосовуючи перетворення по одному.
Парні функції симетричні щодо осі y, тоді як непарні функції симетричні щодо початку.
Навіть функції задовольняють умові$f(x)=f(−x)$.
Непарні функції задовольняють умові$f(x)=−f(−x)$.
Функція може бути непарною, парною або ні.
Функція може бути стиснута або розтягнута вертикально, множивши вихід на константу.
Функція може бути стиснута або розтягнута по горизонталі шляхом множення вхідних даних на константу.
Порядок, в якому застосовуються різні перетворення, впливає на кінцеву функцію. Як вертикальні, так і горизонтальні перетворення повинні застосовуватися в заданому порядку. Однак вертикальне перетворення може поєднуватися з горизонтальним перетворенням в будь-якому порядку.

Глосарій

парна функція

функція, графік якої незмінний горизонтальним відображенням$f(x)=f(−x)$, і симетричний щодо осі y

горизонтальне стиснення - перетворення, яке стискає графік функції по горизонталі, шляхом множення вхідних даних на константу b> 1

горизонтальне відображення — перетворення, яке відображає графік функції по осі y шляхом множення вхідних даних на −1

горизонтальний зсув - перетворення, яке зміщує графік функції вліво або вправо шляхом додавання позитивної або негативної константи до вхідних даних

горизонтальне розтягування - перетворення, яке розтягує графік функції по горизонталі шляхом множення вхідних даних на константу 0 <b<1

непарна функція функція, графік якої незмінний комбінованим горизонтальним і вертикальним відображенням$f(x)=−f(−x)$, і симетричний щодо походження

вертикальне стиснення — перетворення функції, яке стискає графік функції вертикально шляхом множення вихідних даних на константу 0 <a<1

вертикальне відображення — перетворення, яке відображає графік функції по осі x шляхом множення вихідних даних на −1

вертикальний зсув - перетворення, яке зміщує графік функції вгору або вниз, додаючи позитивну або негативну константу до виводу

вертикальне розтягування - перетворення, яке розтягує графік функції по вертикалі шляхом множення вихідних даних на константу a> 1

\(x\)	2	4	6	8
\(f(x)\)	1	3	7	11
\(g(x)\)	-2	0	4	8

\(x\)	5	7	9	11
\(x-3\)	2	4	6	8
\(f(x)\)	1	3	7	11
\(g(x)\)	1	3	7	11

\(x\)	2	4	6	8
\(g(x)\)	\(\dfrac{1}{2}\)	\(\dfrac{3}{2}\)	\(\dfrac{7}{2}\)	\(\dfrac{11}{2}\)

Таблиця\(\PageIndex{8}\)
\(x\)	-2	-4	-6	-8
\(h(x)\)	1	3	7	11

Таблиця\(\PageIndex{11}\)
\(x\)	-2	0	2	-4
\(h(x)\)	15	10	5	20

Таблиця\(\PageIndex{19}\)
\(x\)	2	4	6	8
\(f(3x)\)	10	14	15	17

Таблиця\(\PageIndex{20}\)
\(x\)	2	4	6	8
\(2f(3x)\)	20	28	30	34