2.1: Графіки косинусних і синусоїдних функцій
- Page ID
- 59337
Фокусні питання
Наступні питання призначені для керівництва нашим вивченням матеріалу в цьому розділі. Вивчивши цей розділ, ми повинні зрозуміти поняття, мотивовані цими питаннями, і вміти писати точні, узгоджені відповіді на ці питання.
- Які графіки і важливі властивості графіків\(y = \cos(x)\) і\(y = \sin(x)\)?
- Які області функцій синуса і косинуса? Які діапазони функцій синуса і косинуса?
- Які періоди функцій синуса і косинуса? Що означає період?
- Що таке амплітуда? Як амплітуда впливає на графік синуса або косинуса?
Початок діяльності
Найосновнішою формою малювання графіка функції є побудова точок. Використовуйте значення в наведеній таблиці для побудови точок на графіку,\(y = \sin(x)\) а потім намалюйте графік\(y = \sin(t)\) for\(0 < t < 2\pi\). Примітка: На\(t\) -осі лінії сітки є\(\dfrac{\pi}{12}\) одиницями один від одного, а на\(y\) -осі лінії сітки - 0,1 одиниці один від одного.

| \(t\) | \(\sin(t)\) | \(\sin(t)\)(прибл.) |
|---|---|---|
| \ (t\)» style="вертикальне вирівнювання: середина; "> 0 | \ (\ sin (t)\)» style="вертикальне вирівнювання: середина; "> 0 | \ (\ sin (t)\) (приблизно)» style="вертикальне вирівнювання: середина; "> 0 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{\pi}{6}\) | \ (\ sin (t)\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{1}{2}\) | \ (\ sin (t)\) (приблизно)» style="вертикальне вирівнювання: середина; "> 0.5 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{\pi}{4}\) | \ (\ sin (t)\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{\sqrt{2}}{2}\) | \ (\ sin (t)\) (приблизно)» style="вертикальне вирівнювання: середина; "> 0.707 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{\pi}{3}\) | \ (\ sin (t)\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{\sqrt{3}}{2}\) | \ (\ sin (t)\) (приблизно)» style="вертикальне вирівнювання: середина; "> 0.866 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{\pi}{2}\) | \ (\ sin (t)\)» style="вертикальне вирівнювання: середина; "> 1 | \ (\ sin (t)\) (приблизно)» style="вертикальне вирівнювання: середина; "> 1 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{2\pi}{3}\) | \ (\ sin (t)\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{\sqrt{3}}{2}\) | \ (\ sin (t)\) (приблизно)» style="вертикальне вирівнювання: середина; "> 0.866 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{3\pi}{4}\) | \ (\ sin (t)\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{\sqrt{2}}{2}\) | \ (\ sin (t)\) (приблизно)» style="вертикальне вирівнювання: середина; "> 0.714 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{5\pi}{6}\) | \ (\ sin (t)\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{1}{2}\) | \ (\ sin (t)\) (приблизно)» style="вертикальне вирівнювання: середина; "> 0.5 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\pi\) | \ (\ sin (t)\)» style="вертикальне вирівнювання: середина; "> 0 | \ (\ sin (t)\) (приблизно)» style="вертикальне вирівнювання: середина; "> 0 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{7\pi}{6}\) | \ (\ sin (t)\)» style="вертикальне вирівнювання: середина; ">\(-\dfrac{1}{2}\) | \ (\ sin (t)\) (приблизно)» style="вертикальне вирівнювання: середина; ">-0.5 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{5\pi}{4}\) | \ (\ sin (t)\)» style="вертикальне вирівнювання: середина; ">\(-\dfrac{\sqrt{2}}{2}\) | \ (\ sin (t)\) (приблизно)» style="вертикальне вирівнювання: середина; ">-0,707 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{4\pi}{3}\) | \ (\ sin (t)\)» style="вертикальне вирівнювання: середина; ">\(-\dfrac{\sqrt{3}}{2}\) | \ (\ sin (t)\) (приблизно)» style="вертикальне вирівнювання: середина; ">-0,866 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{3\pi}{2}\) | \ (\ sin (t)\)» style="вертикальне вирівнювання: середина; ">-1 | \ (\ sin (t)\) (приблизно)» style="вертикальне вирівнювання: середина; ">-1 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{5\pi}{3}\) | \ (\ sin (t)\)» style="вертикальне вирівнювання: середина; ">\(-\dfrac{\sqrt{3}}{2}\) | \ (\ sin (t)\) (приблизно)» style="вертикальне вирівнювання: середина; ">-0,866 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{7\pi}{4}\) | \ (\ sin (t)\)» style="вертикальне вирівнювання: середина; ">\(-\dfrac{\sqrt{2}}{2}\) | \ (\ sin (t)\) (приблизно)» style="вертикальне вирівнювання: середина; ">-0,707 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{11\pi}{6}\) | \ (\ sin (t)\)» style="вертикальне вирівнювання: середина; ">\(-\dfrac{1}{2}\) | \ (\ sin (t)\) (приблизно)» style="вертикальне вирівнювання: середина; ">-0.5 |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(2\pi\) | \ (\ sin (t)\)» style="вертикальне вирівнювання: середина; "> 0 | \ (\ sin (t)\) (приблизно)» style="вертикальне вирівнювання: середина; "> 0 |
Ми також можемо використовувати графічний калькулятор або інший графічний пристрій, щоб намалювати графік функції синуса. Переконайтеся, що пристрій встановлено в режимі радіана і використовуйте його, щоб намалювати графік\(y = \sin(t)\) використання\(-2\pi \leq t \leq 4\pi\) і\(-1.2 \leq t \leq 1.2\). Примітка: Багато графічних утиліт вимагають використання в\(x\) якості незалежної змінної. Для таких пристроїв нам потрібно використовувати\(y = \sin(x)\). Це не матиме ніякої різниці в графіку функції.
- Порівняйте це з графіком з частини (1). У чому подібність? Які відмінності?
- Знайти чотири окремих значення,\(t\) де графік синусоїдальної функції перетинає\(t\) -вісь. Такі значення називаються\(t\) - перехоплення синусоїдальної функції (або коренів або нулів).
- Виходячи з графіків, що, здається, є максимальним значенням\(\sin(t)\). Визначте два різних значення\(t\), які дають це максимальне значення\(\sin(t)\).
- Виходячи з графіків, що, здається, є мінімальним значенням\(\sin(t)\). Визначте два різних значення\(t\), які дають це мінімальне значення\(\sin(t)\).
Періоди синусоїдних і косинусних функцій
Одна річ, яку ми можемо спостерігати з графіків синусоїдальної функції на початку діяльності, полягає в тому, що графік, здається, має форму «хвилі» і що ця «хвиля» повторюється, коли ми рухаємося вздовж горизонтальної осі. Ми бачимо, що частина графіка між 0 і\(2\pi\) здається ідентичною частині графіка між\(2\pi\) і\(4\pi\) і до частини графіка між\(-2\pi\) і 0. Графік синусоїдної функції демонструє те, що відоме як періодична властивість. На малюнку 2.1 показаний графік\(y = \sin(t)\) для трьох циклів.
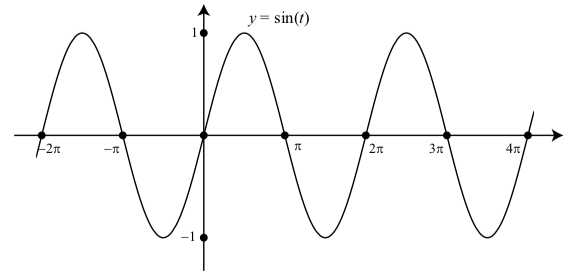
Малюнок\(\PageIndex{1}\): Графік\(y = \sin(t)\) з\(-2\pi \leq t \leq 4\pi\)
Ми говоримо, що функція синуса є періодичною функцією. Такі функції часто використовуються для моделювання повторюваних явищ, таких як маятник, що гойдається вперед і назад, вага, прикріплений до пружини, і вібраційна гітарна струна.
Причина того, що графік\(y = \sin(t)\) повторів полягає в тому, що значення\(\sin(t)\) є y-координатою точки, коли вона рухається навколо одиничного кола. Оскільки окружність одиничного кола є\(2\pi\) одиницями, дуга довжини\((t + 2\pi)\) матиме ту саму кінцеву точку, що і дуга довжини t Оскільки\(\sin(t)\) y-координата цієї точки, ми бачимо, що\(\sin(t + 2\pi) = \sin(t)\). Це означає, що період синусоїдальної функції дорівнює\(2\pi\). Далі наведено більш формальне визначення періодичної функції.
Визначення
Визначення. Функція\(f\) є періодичною з періодом\(p\) якщо\(f(t + p) = f(t)\) для всіх\(t\) в області\(f\) і\(p\) є найменшим додатним числом, яке має цю властивість.
Зверніть увагу, що якщо\(f\) періодична функція з періодом\(p\), то якщо ми додамо 2\(p\) до\(t\), ми отримуємо\[f(t + 2p) = f((t+p)+p) = f(t + p) =f(t).\]
Ми можемо продовжувати повторювати цей процес і бачити, що для будь-якого цілого числа\(k\),\[f(t + kp) =f(t).\]
Поки ми обговорювали лише функцію синуса, але ми отримуємо подібну поведінку з функцією косинуса. Нагадаємо, що функція обгортання обертає числову лінію навколо одиничного кола таким чином, що повторюється в відрізках довжини\(2\pi\). Це періодична поведінка і призводить до періодичної поведінки як синусоїдних, так і косинусних функцій, оскільки значенням синусоїдальної функції є\(y\) -координата точки на одиничному колі, а значенням функції косинуса є\(x\) -координата тієї ж точки на одиничному колі, синус і функції косинуса повторюються кожен раз, коли ми робимо одне обтікання навколо одиничного кола. Тобто,\[\cos(t + 2\pi) = \cos(t) \space and \space \sin(t + 2\pi) = \sin(t).\]
Важливо визнати, що\(2\pi\) це найменша кількість, яка робить це станеться. Тому функції косинуса і синуса періодичні з періодом\(2\pi\).
Вправа\(\PageIndex{1}\)
Ми можемо, звичайно, використовувати графічну утиліту, щоб намалювати графік функції косинуса. Однак це допомагає зрозуміти графік, якщо ми насправді малюємо графік вручну, як ми робили для функції синуса на початку діяльності. Використовуйте значення в наведеній таблиці для побудови точок на графіку,\(y = \cos(t)\) а потім намалюйте графік\(y = \cos(t)\) for\(0 \leq t \leq 2\pi\).

| \(t\) | \(\cos(t)\) | \(\cos(t)\)(приблизно) |
|---|---|---|
| \ (t\) ">\(0\) | \ (\ cos (t)\) ">\(1\) | \ (\ cos (t)\) (приблизно) ">\(1\) |
| \ (t\) ">\(\dfrac{\pi}{6}\) | \ (\ cos (t)\) ">\(\dfrac{\sqrt{3}}{2}\) | \ (\ cos (t)\) (приблизно) ">\(0.866\) |
| \ (t\) ">\(\dfrac{\pi}{4}\) | \ (\ cos (t)\) ">\(\dfrac{\sqrt{2}}{2}\) | \ (\ cos (t)\) (приблизно) ">\(0.707\) |
| \ (t\) ">\(\dfrac{\pi}{3}\) | \ (\ cos (t)\) ">\(\dfrac{1}{2}\) | \ (\ cos (t)\) (приблизно) ">\(0.5\) |
| \ (t\) ">\(\dfrac{\pi}{2}\) | \ (\ cos (t)\) ">\(0\) | \ (\ cos (t)\) (приблизно) ">\(0\) |
| \ (t\) ">\(\dfrac{2\pi}{3}\) | \ (\ cos (t)\) ">\(-\dfrac{1}{2}\) | \ (\ cos (t)\) (приблизно) ">\(-0.5\) |
| \ (t\) ">\(\dfrac{3\pi}{4}\) | \ (\ cos (t)\) ">\(-\dfrac{\sqrt{2}}{2}\) | \ (\ cos (t)\) (приблизно) ">\(-0.714\) |
| \ (t\) ">\(\dfrac{5\pi}{6}\) | \ (\ cos (t)\) ">\(-\dfrac{\sqrt{3}}{2}\) | \ (\ cos (t)\) (приблизно) ">\(-0.866\) |
| \ (t\) ">\(\pi\) | \ (\ cos (t)\) ">\(-1\) | \ (\ cos (t)\) (приблизно) ">\(-1\) |
| \ (t\) ">\(\dfrac{7\pi}{6}\) | \ (\ cos (t)\) ">\(-\dfrac{\sqrt{3}}{2}\) | \ (\ cos (t)\) (приблизно) ">\(-0.866\) |
| \ (t\) ">\(\dfrac{5\pi}{4}\) | \ (\ cos (t)\) ">\(-\dfrac{\sqrt{2}}{2}\) | \ (\ cos (t)\) (приблизно) ">\(-0.714\) |
| \ (t\) ">\(\dfrac{4\pi}{3}\) | \ (\ cos (t)\) ">\(-\dfrac{1}{2}\) | \ (\ cos (t)\) (приблизно) ">\(-0.5\) |
| \ (t\) ">\(\dfrac{3\pi}{2}\) | \ (\ cos (t)\) ">\(0\) | \ (\ cos (t)\) (приблизно) ">\(-1\) |
| \ (t\) ">\(\dfrac{5\pi}{3}\) | \ (\ cos (t)\) ">\(\dfrac{1}{2}\) | \ (\ cos (t)\) (приблизно) ">\(0.5\) |
| \ (t\) ">\(\dfrac{7\pi}{4}\) | \ (\ cos (t)\) ">\(-\dfrac{\sqrt{2}}{2}\) | \ (\ cos (t)\) (приблизно) ">\(0.707\) |
| \ (t\) ">\(\dfrac{11\pi}{6}\) | \ (\ cos (t)\) ">\(\dfrac{\sqrt{3}}{2}\) | \ (\ cos (t)\) (приблизно) ">\(-0.866\) |
| \ (t\) ">\(2\pi\) | \ (\ cos (t)\) ">\(1\) | \ (\ cos (t)\) (приблизно) ">\(1\) |
- Відповідь
-
Не всі точки побудовані, але нижче наведено графік одного повного періоду\(y = \cos(t)\) for\(0 \leq t \leq 2\pi\).
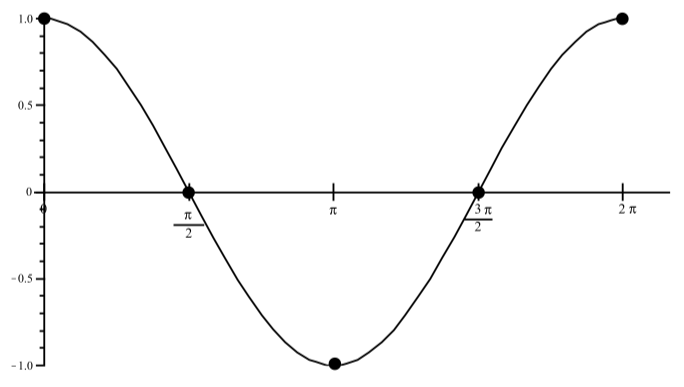
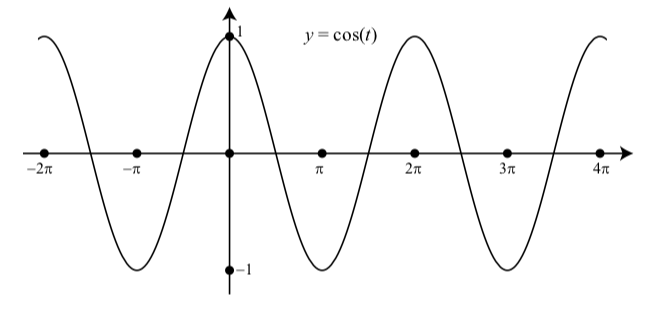
Малюнок\(\PageIndex{2}\): Графік\(y = \cos(t)\) з\(-2\pi \leq t \leq 4\pi\)
Вправа\(\PageIndex{2}\)
- Порівняйте графік на малюнку\(\PageIndex{2}\) з графіком з вправи\(\PageIndex{1}\). У чому подібність? Які відмінності?
- Знайти чотири окремих значення того,\(t\) де графік косинусної функції перетинає\(t\) -вісь. Такі значення називаються\(t\) - перехоплення функції косинуса (або коренів або нулів).
- Виходячи з графіків, що, здається, є максимальним значенням\(\cos(t)\). Визначте два різних значення\(t\), які дають це максимальне значення\(\cos(t)\).
- Виходячи з графіків, що, здається, є мінімальним значенням\(\cos(t)\). Визначте два різних значення\(t\), які дають це мінімальне значення\(\cos(t)\).
- Відповідь
-
- Різниця полягає в тому, що графік на малюнку\(\PageIndex{2}\) показує три повних періоди\(y = \cos(t)\) над інтервалом\([-2\pi, 4\pi]\).
- Графік\(y = \cos(t)\) has\(t\) -перехоплює в\(t = -\dfrac{3\pi}{2}, t = -\dfrac{\pi}{2}, t = \dfrac{\pi}{2}, t = \dfrac{3\pi}{2}, t = \dfrac{5\pi}{2}\), і\(t = \dfrac{7\pi}{2}\)
- Максимальне значення\(y = \cos(t)\) дорівнює\(1\). Графік досягає цього максимуму при\(t = -2\pi, t = 0, t = 2\pi\), і\(t = 4\pi\).
- Мінімальне значення\(y = \cos(t)\) є\(-1\). Графік досягає цього мінімуму при\(t = -\pi, t = \pi\), і\(t = 3\pi\)
Діяльність 2.3 (Графіки синусоїдних і косинусних функцій).
Тепер ми побудували графік синусоїдних і косинусних функцій шляхом побудови точок і за допомогою графічної утиліти. Ми можемо краще зрозуміти ці графіки, якщо побачимо, як ці графіки пов'язані з визначеннями одиничного кола\(\sin(t)\) і\(\cos(t)\). Ми будемо використовувати два аплети Geogebra, щоб допомогти нам зробити це.
Перший аплет називається Генератор синусоїдальних графів. Веб-адреса - gvsu.edu/s/ly
Для початку просто перемістіть повзунок до тих пір,\(t\) поки не отримаєте\(t = 1\) і спостерігайте за отриманим зображенням. Зліва буде копія одиничного кола з намальованою дугою, яка має довжину\(1\). Також буде відображена\(y\) координата кінцевої точки цієї дуги (\(0.84\)округлена до найближчої сотої). Горизонтальна лінія буде з'єднана з точкою\((1, 0.84)\) на графіку\(y = \sin(t)\). Оскільки значення\(t\) змінюються повзунком, більше точок буде намальовано таким чином на графіку\(y = \sin(t)\).
Інший аплет називається генератором косинусних графів, і він працює подібно до генератора синусоїдних графів. Веб-адреса для цього аплету http://gvsu.edu/s/Lz
Властивості графів синусоїдних і косинусних функцій
Графіки\(y = \sin(t)\) і\(y = \cos(t)\) називаються синусоїдальними хвилями, а синусоїдальні і косинусні функції називаються синусоїдальними функціями. Обидві ці конкретні синусоїдальні хвилі мають період\(2\pi\). Графік за один період називається циклом графіка. Як і у випадку з іншими функціями в нашому попередньому дослідженні алгебри, ще однією важливою властивістю графіків є їх перехоплення, зокрема, горизонтальні перехоплення або точки, де графік перетинає горизонтальну вісь. Одна велика відмінність від алгебри полягає в тому, що функції синуса і косинуса мають нескінченно багато горизонтальних перехоплень.
У\(\PageIndex{2}\) Вправі ми використовували Figure\(\PageIndex{2}\) і\(-\dfrac{\pi}{2}, \dfrac{\pi}{2}, \dfrac{3\pi}{2}, \dfrac{5\pi}{2}, \dfrac{7\pi}{2}\) визначили, що є\(t\) -перехоплення на графіку\(y = \cos(t)\). Зокрема, в\([0, 2\pi]\) інтервалі єдиними\(t\) -перехопленнями\(y = \cos(t)\) є\(t = \dfrac{\pi}{2}\) і\(t = \dfrac{3\pi}{2}\).
Є, звичайно, і інші\(t\) -перехоплення, і саме тут\(2\pi\) корисний період. Ми можемо генерувати будь-який інший\(t\) -перехоплення\(y = \cos(t)\) шляхом додавання цілих кратних періоду\(2\pi\) до цих двох значень. Наприклад, якщо додати\(6\pi\) до кожного з них, ми побачимо, що\(t = \dfrac{13\pi}{2}\) і\(t = \dfrac{15\pi}{2}\) є\(t\) перехопленнями\(y = \cos(t)\).
Вправа\(\PageIndex{3}\)
Використовуйте графік, щоб визначити\(t\) -перехоплення\(y = \sin(t)\) в інтервалі\([0, 2\pi]\). Потім використовуйте властивість періоду функції синуса для визначення\(t\) -перехоплення\(y = \sin(t)\) в інтервалі\([-2\pi, 4\pi]\). Порівняйте цей результат з графіком на малюнку 2.1. Нарешті, визначте два\(t\) -перехоплення\(y = \sin(t)\), які не знаходяться в інтервалі\([-2\pi, 4\pi]\).
- Відповідь
-
Графік\(y = \sin(t)\) has\(t\) -перехоплення\(t = 0, t = \pi\), і\(t = 2\pi\) в інтервалі\([0, 2\pi]\).
Якщо додати період\(2\pi\) до кожного з цих\(t\) -перехоплень і відняти період\(2\pi\) від кожного з цих\(t\) -перехоплень, ми бачимо, що графік\(y = \sin(t)\) має\(t\) -перехоплення\(t = -2\pi, t = -\pi, t = 0, t = \pi, t = 2\pi, t = 3\pi\), і\(t = 4\pi\) в інтервалі\([-2\pi, 4\pi]\).Ми можемо визначити інші\(t\) -перехоплення\(y = \sin(t)\) шляхом багаторазового додавання або віднімання періоду\(2\pi\). Наприклад, існує\(t\) -перехоплення за адресою:
- \(t = 3\pi + 2\pi = 5\pi\)
- \(t = 5\pi + 2\pi = 7\pi\)
Однак, якщо ми більш уважно подивимося на графік, то побачимо\(y = \sin(t)\), що\(t\) -перехоплення рознесені\(\pi\) одиниці один від одного. Це означає, що ми можемо сказати\(t = 0 + k\pi\), що, де\(k\) деяке ціле число, це\(t\) -перехоплення\(y = \sin(t)\).
Діяльність 2.5 (Вивчення графіків синусоїдних функцій)
Виконайте одну з наступних дій:
- Намалюйте графіки\(y = \sin(t)\),\(y = \dfrac{1}{2}\sin(t)\) і\(y = 2\sin(t)\),\(y = -\sin(t)\), і\(y = 2\sin(t)\) на однакових осях. Переконайтеся, що ваша графічна утиліта знаходиться в режимі радіана і використовувати\(-2\pi \leq x \leq 2\pi\) і\(-2.5 \leq x \leq 2.5\).
- Скористайтеся аплетом Geogebra амплітуда синусоїди за наступною веб-адресою: http://gvsu.edu/s/LM
Вираз для\(g(t)\) можна змінити, але залиште його встановленим у значення\(g(t) = \sin(t)\). Повзунок можна пересунути, щоб змінити значення A, і графік\(y = A\sin(t)\) буде намальований. Дослідіть ці графіки, змінюючи значення A, переконавшись, що використовуються від'ємні значення A, а також позитивні значення A (Це можна змінити на\(g(t) = \cos(t)\) і вивчити графіки\(y = A\sin(t)\).
Амплітуда синусоїдних і косинусних функцій
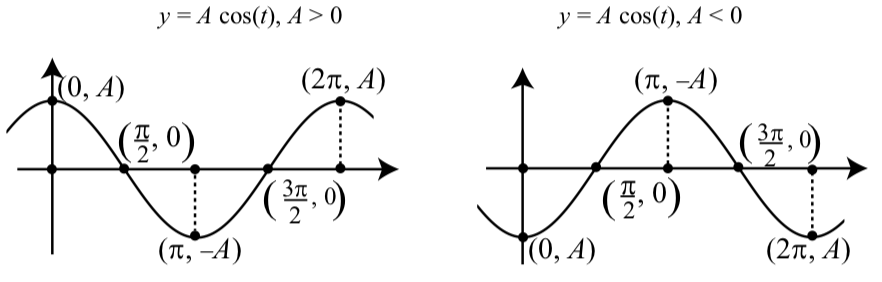
Графіки функцій з Activity 2.5 повинні були виглядати як один з графіків на малюнку 2.3. Обидва графіки є графіками\(y = A\sin(t)\), але той, що зліва - для,\(A > 0\) а той, що праворуч - для\(A < 0\). Зверніть увагу, що коли\(A < 0\),\(-A > 0\). Ще одна важлива характеристика синусоїдальної хвилі - амплітуда. Амплітуда кожного з графіків на малюнку 2.3 представлена довжиною пунктирних ліній, і ми бачимо, що ця довжина дорівнює\(|A|\).
Визначення: амплітуда
Амплітуда синусоїдальної хвилі дорівнює половині відстані між максимальним і мінімальним функціональними значеннями.
\[\text{Amplitude} = \dfrac{1}{2}|(\text{ max y-coordinate}) - (\text{min y-coordinate})|\]
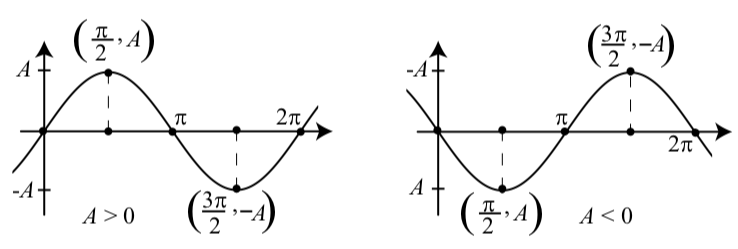
Малюнок\(\PageIndex{3}\): Графіки\(y = A\sin(t)\)
Вправа\(\PageIndex{4}\)
Намалюйте графіки\(y = A\cos(t)\) для\(A > 0\) та для\(A < 0\) аналогічних графікам на\(y = A\sin(t)\) малюнку\(\PageIndex{3}\).
- Відповідь
-
Використання утиліти графіків
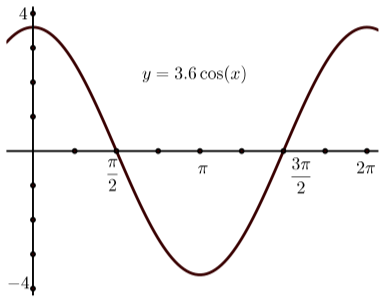
Ми часто будемо використовувати графічну утиліту, щоб намалювати графік синусоїдальної функції. При цьому рекомендується використовувати амплітуду, щоб допомогти встановити відповідне вікно перегляду. Основна ідея полягає в тому, щоб екран на графічній утиліті показував трохи більше одного періоду синусоїди. Наприклад, якщо ми намагаємося намалювати графік\(y = 3.6\cos(t)\), ми могли б використовувати наступне вікно перегляду. \[-0.5 \leq x \leq 6.5 \space and \space -4 \leq y \leq 4.\]Якщо це можливо, встановіть позначки\(x\) -tickmarks як кожні\(\dfrac{\pi}{4}\) або\(\dfrac{\pi}{2}\) одиниці.
Вправа\(\PageIndex{5}\)
- Використовуйте утиліту графіків, щоб намалювати графік\(y = 3.6\cos(t)\) використання вікна перегляду, зазначеного перед цим тестом прогресу.
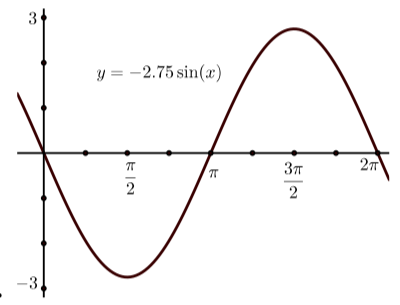
- Використовуйте утиліту графіки, щоб намалювати графік\(y = -2.75\sin(t)\).
- Відповідь
-
1.
2.
Симетрія та негативні ідентичності
Вивчіть графік,\(y = \cos(t)\) показаний на малюнку 2.2. Якщо ми зосередимось на цій частині графіка між\(-2\pi\) і\(2\pi\), ми можемо помітити, що ліва сторона графіка є «дзеркальним відображенням» правої частини графіка. Щоб побачити це краще, скористайтеся аплетом Geogebra симетрія графіка\(y = \cos(t)\) за наступним посиланням: http://gvsu.edu/s/Ot
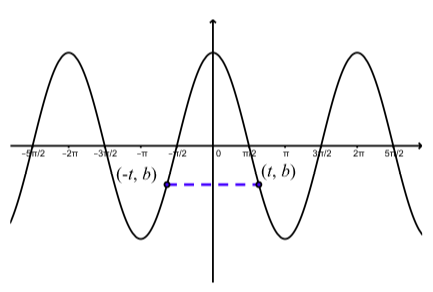
Малюнок\(\PageIndex{4}\): Графік, що показує симетрію\(y = \cos(t)\)
\(\PageIndex{4}\)На малюнку показано типове зображення з цього аплету. Оскільки друга координата точки на графіку є значенням функції в першій координаті, ця цифра (і аплет) вказує на те, що\(b = \cos(t)\) і\(b = \cos(-t)\). Тобто це ілюструє той факт, що\(\cos(-t) = \cos(t)\). Наступна діяльність дає пояснення, чому це правда.
Діяльність 2.8: Позитивні та негативні дуги
Для цієї діяльності ми будемо використовувати аплет Geogebra під назвою Малювання позитивної дуги та негативної дуги на одиничному колі. Посилання на цей аплет http://gvsu.edu/s/Ol
Оскільки повзунок для\(t\) в аплеті використовується, дуга довжини t буде намальована синім кольором, а дуга довжини\(-t\) буде намальована червоним кольором. Крім того,\(-t\) будуть відображатися координати кінцевих точок обох дуг\(t\) і. Вивчіть координати цих двох точок для різних значень\(t\). Що ви спостерігаєте? Маючи на увазі, що координати цих точок також можуть бути представлені у вигляді\[(\cos(t), \sin(t))\space and \space (\cos(-t), \sin(-t)),\]
що це, здається, вказує на відносини між\(\cos(-t)\) і\(\cos(t)\)? А як щодо відносин між\(\sin(-t)\) і\(\sin(t)\)?
\(\PageIndex{5}\)На малюнку показана типова ситуація, проілюстрована в діяльності 2.8. Дуга та відповідна їй негативна дуга були намальовані на одиничному колі. Що ми бачили
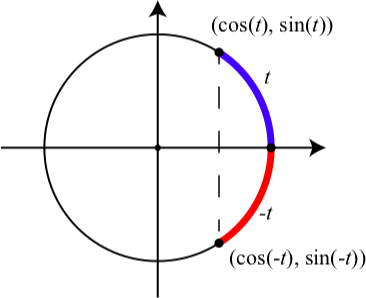
Малюнок\(\PageIndex{5}\): Дуга і негативна дуга на одиничному колі
полягає в тому, що якщо кінцева точка дуги\(t\) є\((a, b)\), то по симетрії кола, ми бачимо, що кінцева точка дуги\(-t\) є\((a, -b)\). Отже, діаграма ілюструє наступні результати, які іноді називають негативними тотожностями дуги.
Визначення: Негативні дугові ідентичності
Для кожного дійсного числа\(t\)\[\sin(-t) = -\sin(t) \space \cos(-t) = \cos(t).\]
Для подальшої перевірки від'ємних тотожностей дуги для синуса та косинуса скористайтеся утилітою графіків, щоб:
- Намалюйте графік\(y = \cos(-x)\) використання\(0 \leq x \leq 2\pi\). Графік повинен бути ідентичним графіку\(y = \cos(x)\).
- Намалюйте графік\(y = \sin(-x)\) використання\(0 \leq x \leq 2\pi\). Графік повинен бути ідентичним графіку\(y = \sin(x)\).
Ці так звані негативні дугові ідентичності дають нам можливість подивитися на симетрію графіків косинусних і синусоїдних функцій. Симетрію функції косинуса ми вже проілюстрували на рис\(\PageIndex{4}\). Через це, ми говоримо, що графік симетричний щодо осі Y.\(y = \cos(t)\)
А як щодо симетрії в графіку синусоїдальної функції? Малюнок\(\PageIndex{6}\) ілюструє, що\(\sin(-t) = \sin(t)\) означає негативна ідентичність щодо симетрії\(y = \sin(t)\). У цьому випадку ми говоримо,\(y = \sin(t)\) що графік симетричний щодо походження.
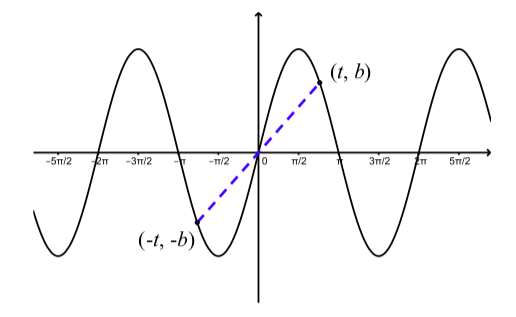
Малюнок\(\PageIndex{6}\): Графік, що показує симетрію\(y = \sin(t)\).
Щоб краще побачити симетрію графіка синусоїдальної функції, скористайтеся аплетом Geogebra Симетрія графа\(y = \sin(t)\) за наступним посиланням: http://gvsu.edu/s/Ou
Резюме
У цьому розділі ми вивчили наступні важливі поняття та ідеї:
- Важливі характеристики синусоїдальних функцій мають форму\(y = A\sin(t)\) або\(y = A\cos(t)\) наведені в таблиці 2.1.
- Інформація в таблиці 2.1 може здатися, що багато запам'ятовується, і насправді в наступних розділах ми отримаємо набагато більше інформації про синусоїдальні хвилі. Тому замість того, щоб намагатися запам'ятати все в таблиці 2.1, краще запам'ятати основні форми графіків, як показано на малюнку\(\PageIndex{7}\) та малюнку\(\PageIndex{8}\).
| \(y = A\sin(t)\) | \(y = A\cos(t)\) | |
|---|---|---|
| \ (y = A\ sin (t)\) ">Усі дійсні числа | домен | \ (y = A\ cos (t)\) ">Усі дійсні числа |
| \ (y = A\ sin (t)\) ">\(2\pi\) | період | \ (y = А\ cos (t)\) ">\(2\pi\) |
| \ (y = A\ sin (t)\) ">\(|A|\) | амплітуда | \ (y = А\ cos (t)\) ">\(|A|\) |
| \ (y = A\ sin (t)\) ">\((0, 0)\) | \(y\)-перехопити | \ (y = А\ cos (t)\) ">\((0, A)\) |
| \ (y = A\ sin (t)\) ">\(t = 0\) і\(t = \pi\) | \(t\)-перехоплення в\([0, 2\pi)\) | \ (y = А\ cos (t)\) ">\(t = \dfrac{\pi}{2}\) і\(t = \dfrac{3\pi}{2}\) |
| \ (y = A\ sin (t)\) ">\(|A|\) | максимальне значення | \ (y = А\ cos (t)\) ">\(|A|\) |
| \ (y = A\ sin (t)\) ">\(-|A|\) | мінімальне значення | \ (y = А\ cos (t)\) ">\(-|A|\) |
| \ (y = A\ sin (t)\) ">Інтервал\([-|A|, |A|]\) | діапазон | \ (y = A\ cos (t)\) ">Інтервал\([-|A|, |A|]\) |
| \ (y = A\ sin (t)\) ">\(t = \dfrac{\pi}{2}\) | коли\(A > 0\), максимум відбувається при | \ (y = А\ cos (t)\) ">\(t = 0\) |
| \ (y = A\ sin (t)\) ">\(t = \dfrac{3\pi}{2}\) | коли\(A > 0\), максимум відбувається при | \ (y = А\ cos (t)\) ">\(t = \pi\) |
| \ (y = A\ sin (t)\) ">\(t = \dfrac{3\pi}{2}\) | коли\(A < 0\), максимум відбувається при | \ (y = А\ cos (t)\) ">\(t = \pi\) |
| \ (y = A\ sin (t)\) ">\(t = \dfrac{\pi}{2}\) | коли\(A < 0\), максимум відбувається при | \ (y = А\ cos (t)\) ">\(t = 0\) |
| \ (y = A\ sin (t)\) ">походження | симетрія щодо | \ (y = A\ cos (t)\) "\(y\)>-вісь |
- Один із способів запам'ятати розташування галочок на\(t\) осі -це запам'ятати інтервал для цих галочок становить одну чверть періоду, а період -\(2\pi\). Отже, інтервал\(\dfrac{2\pi}{4} = \dfrac{\pi}{2}\).
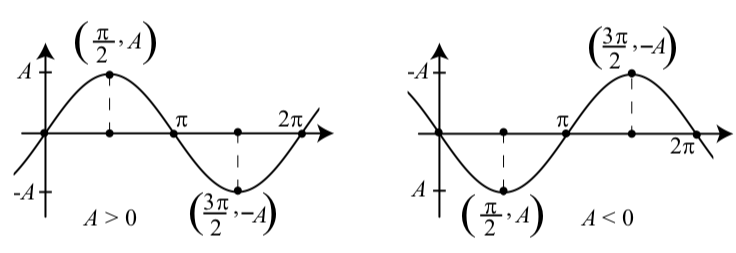
Малюнок\(\PageIndex{7}\): Графіки\(y = A\sin(t)\).
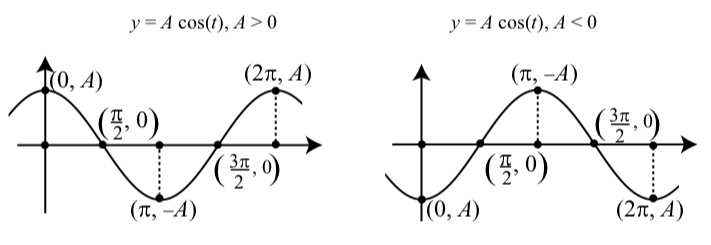
Малюнок\(\PageIndex{8}\): Графіки\(y = A\cos(t)\).
Додатковий матеріал - парні та непарні функції
Існує більш загальний математичний контекст для цих типів симетрії, і це пов'язано з тим, що називаються парними функціями та непарними функціями.
Визначення: парні та непарні функції
- Функція\(f\) є парною функцією, якщо\(f(-x) = f(x)\) для всіх\(x\) в області\(f\).
- Функція\(f\) є непарною функцією, якщо\(f(-x) = -f(x)\) для всіх\(x\) в області\(f\).
Таким чином, з цими визначеннями, ми можемо сказати, що функція косинус парна функція і синус функція непарна функція. Чому ми використовуємо ці терміни? Одне з пояснень полягає в тому, що поняття парних і непарних функцій використовуються для опису функцій\(f\) виду\(f(x) = x^n\) для деякого позитивного цілого числа\(n\), а графіки цих функцій демонструють різні типи симетрії, коли\(n\) парна, а коли\(n\) непарна.
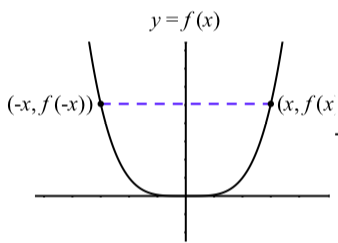
Малюнок\(\PageIndex{9}\):\(f(x) = x^n\) n парні і\(f(-x) = f(x)\)
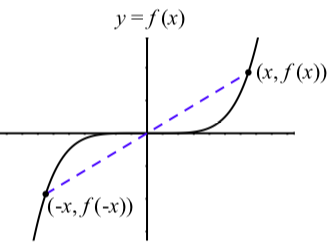
Малюнок\(\PageIndex{10}\):\(f(x) = x^n\),\(n\) непарні і\(f(-x) = -f(x)\).
На малюнку ми бачимо\(\PageIndex{9}\), що коли\(n\) рівний,\(f(-x) = f(x)\) так як\((-x)^n = x^n\). Таким чином, графік симетричний щодо\(y\) -осі. Коли\(n\) непарний, як на малюнку\(\PageIndex{10}\),\(f(-x) = -f(x)\) так як\((-x)^n = -x^n\). Таким чином, графік симетричний щодо походження. Ось чому ми використовуємо термін парні функції для тих функцій,\(f\) для яких\(f(-x) = f(x)\), і ми використовуємо термін непарні функції для тих функцій, для яких\(f(-x) = -f(x)\).
