11.5: Додатки

П'ятиступінчастий метод

При вирішенні практичних завдань часто зручніше вводити дві змінні, а не тільки одну. Дві змінні слід вводити лише тоді, коли в задачі можна знайти дві зв'язки. Кожне співвідношення дасть рівняння, і система з двох рівнянь у двох змінних призведе.

Для вирішення цих проблем ми будемо використовувати п'ятикроковий метод.

1. Введіть дві змінні, по одній для кожної невідомої кількості.
2. Шукайте два відносини всередині проблеми. Переведіть словесні фрази в математичні вирази, щоб сформувати два рівняння.
3. Вирішити отриману систему рівнянь.
4. Перевірте розчин.
5. Напишіть висновок.

Набір зразків A (Числові проблеми)

Приклад$\PageIndex{1}$

Сума двох чисел дорівнює$37$. Одне число$5$ більше іншого. Які бувають цифри?

Крок 1:

Нехай$x =$ менше число.

Нехай$y =$ більше число.

Крок 2: Є два відносини.

а) Сума дорівнює$37$

$x + y = 37$

б) Одна$5$ більша за іншу.

Крок 3:

\ (\ лівий\ {\ begin {масив} {r}
x + y = 37\\
y = x + 5
\ end {масив}\ вправо.\)

Ми можемо легко вирішити цю систему шляхом підміни. $x + 5$Замінюємо$y$ в рівнянні 1.

\ (\ почати {вирівняний}
х + (х + 5) & = 37\\
x + x + 5 &= 37\\
2x + 5 &= 37\\
2x &= 32\\
x &= 16 &\ текст {Потім,} y = 16 + 5 = 21\\
x &= 16
\ кінець {вирівняний}

Крок 4: Сума, якщо$37$.

\ (\ begin {вирівняний}
x + y &= 37\\
16 + 21 &= 37\ текст {Це правильно? }\\
37 &= 37\ текст {Так, це правильно.}
\ end {вирівняний}\)

Один$5$ більший за інший.

\ (\ begin {
вирівняний} y &= x + 5\\
21 &= 16 + 5\\
21 &= 21\ текст {Так, це правильно.}
\ end {вирівняний}\)

Крок 5: Два числа$16$ і$21$.

Практика Набір A

Завдання практики$\PageIndex{1}$

Різниця двох чисел дорівнює 9, а сума тих же двох чисел - 19. Які два числа?

Крок 1:


Крок 2:


Крок 3:


Крок 4:


Крок 5:

Відповідь

Два числа - 14 і 5.

Проблеми вартості та курсу: Проблеми з монетами та проблеми із сумішшю

Проблеми в наборах зразків B і C є задачами значення. Вони називаються задачами вартості, оскільки одне з рівнянь системи, що використовується при їх вирішенні, генерується шляхом розгляду значення, або швидкості, або кількості разів на кількість.

Набір зразків B (Проблеми з монетами)

Приклад$\PageIndex{2}$

Паркувальний лічильник містить 27 монет, що складаються тільки з копійок і чвертей. Якщо лічильник містить $4.35, скільки з кожного типу монет є?

Крок 1:

Нехай$D =$ кількість копійок.

Нехай$Q =$ кількість чвертей.

Крок 2: Є два відносини.

а) Є 27 монет. $D + Q = 27$.

б) Внесок у розмірі копійок =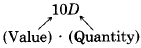

Внесок за кварталами =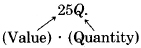

$10D + 25Q = 435$

Крок 3:

\ (\ ліворуч\ {\ почати {масив} {r}
D + Q = 27\\
10D + 25Q = 435
\ кінець {масив}\ вправо.\)

Ми можемо вирішити цю систему, використовуючи ліквідацію шляхом додавання. Помножте обидві сторони рівняння (1) на$-10$ і додайте.

\ (\ почати {масив} {c}
-10 Д-10 Q = -270\\
10 D+25 Q = 435\
\ hline 15 Q = 165\\
Q = 11
\ кінець {масив}\)

Потім,\ (D + 11 = 27\\
D = 16\)

$D = 16, Q = 11$

Крок 4:16 копійок і 11 чвертей - 27 монет.

\ (\ begin {вирівняний}
10 (16) + 11 (25) &= 435\ текст {Це правильно? }\\
160 + 275 &= 435\ текст {Це правильно? }\\
435 &= 435\ текст {Так, це правильно.}
\ end {вирівняний}\)

Рішення перевіряє.

Крок 5: Є 11 чвертей і 16 копійок.

Практика Set B

Завдання практики$\PageIndex{2}$

Мішок містить тільки нікелі і копійки. Вартість колекції становить 2 долари. Якщо є 26 монет у всіх, скільки з кожної монети є?

Відповідь

Є 14 копійок і 12 нікелів.

Набір зразків C (проблеми із сумішшю)

Приклад$\PageIndex{3}$

Студенту-хіміку потрібно 40 мілілітрів (мл) 14% розчину кислоти. Вона мала два кислотні розчини, А і В, щоб змішати разом, утворюючи 40 мл кислотного розчину. Кислотний розчин А - 10% кислота, а розчин кислоти В - 20% кислота. Скільки кожного розчину потрібно використовувати?

Крок 1:

Нехай$x =$ кількість мл - це розчин А.

Нехай$y =$ кількість мл розчину B.

Крок 2: Є два відносини

а) Сума кількості мл двох розчинів дорівнює 40.

$x + y = 40$.

б) Для визначення другого рівняння намалюйте картину ситуації

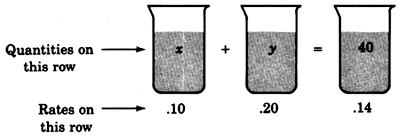
Рівняння випливає безпосередньо з креслення, якщо ми використовуємо ідею кількості разів на кількість.

Крок 3:$.10x + .20y = .14(40)$

\ (\ лівий\ {\ begin {масив} {r}
x + y = 40\\
.10x + .20y = .14 (40)
\ end {масив}\ вправо.\)

\ (\ лівий\ {\ begin {масив} {r}
x + y = 40\\
.10x + .20y = .14 (40)
\ end {масив}\ вправо.\)

Вирішити цю систему шляхом додавання. По-перше, усуньте десяткові числа в рівнянні 2, помноживши обидві сторони на 100.

\ (\ ліворуч\ {\ begin {масив} {r}
х + y = 40\\
10x + 20y = 14 (40)
\ end {масив}\ вправо.\)

Усунути$x$ шляхом множення рівняння 1 на,$-10$ а потім додавання.

\ (\ begin {масив} {c}
-10 x-10 y=-400\
10 x+20 y=560
\\ hline 10 y=160\
y=16
\ end {масив}\)

Потім,\ (х + 16 = 40\\
х = 24\)

$x = 24, y = 16$

Крок 4:24 мл і 16 мл додати до 40 мл.

\ (\ begin {вирівняний}
10 (24) + 20 (16) &= 560\ текст {Це правильно? }\\
240 + 320 &= 560\ текст {Це правильно? }\\
560 &= 560\ текст {Так, це правильно.}
\ end {вирівняний}\)

Рішення перевіряє.

Крок 5: Студент повинен використовувати 24 мл кислотного розчину А і 16 мл розчину кислоти В.

Практика Set C

Завдання практики$\PageIndex{3}$

Студенту-хіміку потрібно 60 мл 26% розчину солі. У нього є два сольові розчини, А і В, щоб змішати разом, утворюючи 60 мл розчину. Сольовий розчин А - 30% солі, а розчин солі В - 20% солі. Скільки кожного розчину потрібно використовувати?

Відповідь

Учень повинен використовувати 36 мл розчину солі А і 24 мл розчину солі В.

вправи

Вправа$\PageIndex{1}$

Сума двох чисел дорівнює 22. Одне число на 6 більше іншого. Які бувають цифри?

Відповідь

Два числа - 14 і 8.

Вправа$\PageIndex{2}$

Сума двох чисел дорівнює 32. Одне число на 8 більше іншого. Які бувають цифри?

Вправа$\PageIndex{3}$

Різниця двох чисел дорівнює 12 і одне число в три рази більше іншого. Які цифри?

Відповідь

Два числа - 18 і 6.

Вправа$\PageIndex{4}$

Різниця двох чисел дорівнює 9 і одного числа в 10 разів більше іншого. Які цифри?

Вправа$\PageIndex{5}$

Половина суми двох чисел дорівнює 14, а половина різниці дорівнює 2. Які бувають цифри?

Відповідь

Цифри - 16 і 12.

Вправа$\PageIndex{6}$

Третина від суми двох чисел дорівнює 6, а п'ята частина різниці дорівнює 2. Які бувають цифри?

Вправа$\PageIndex{7}$

14-фунтова суміш винограду продається за 3,10 долара. Виноград типу 1 продається за 25 центів за фунт, а виноград типу 2 продається за 20 центів за фунт. Скільки фунтів кожного виду винограду було використано?

Відповідь

6 фунтів типу 1 і 8 фунтів типу 2.

Вправа$\PageIndex{8}$

Вартість 80 літрів змішаного миючого розчину становить 28 доларів. Рішення типу 1 коштує 20¢ літр, а рішення типу 2 коштує 40 центів на літр. Скільки літрів кожного розчину було використано для формування змішаного розчину?

Вправа$\PageIndex{9}$

Вартість 42 грам певної хімічної сполуки становить 14,40$. Хімічні витрати типу 1 45¢ на грам, а хімічні витрати типу 2 30¢ за грам. Скільки грамів кожної хімічної речовини було використано для утворення з'єднання?

Відповідь

12 грам типу 1 і 30 грам типу 2.

Вправа$\PageIndex{10}$

У виставі взяли участь 342 людини, деякі дорослі і деякі діти. Вхід для дорослих становив $1.50, а для дітей 75¢. Скільки дорослих і скільки дітей відвідало виставу?

Вправа$\PageIndex{11}$

200 квитків було продано на щорічний музичний спектакль коледжу. Квитки для студентів становили $2.50, а для нестудентів - $3.50. Загальна зібрана сума склала 537 доларів. Скільки нестуденти придбали квитки на виставу?

Відповідь

37 нестудентських квитків.

Вправа$\PageIndex{12}$

Студенту хімії потрібно 22 мл 38% розчину кислоти. У неї є два кислотні розчини, А і В, щоб змішати разом, утворюючи розчин. Кислотний розчин А - це 40% кислота, а розчин кислоти В - 30% кислоти. Скільки кожного розчину потрібно використовувати?

Вправа$\PageIndex{13}$

Студенту-хіміку потрібно 50 мл 72% розчину солі. У нього є два сольові розчини, А і В, щоб змішати разом, щоб утворився розчин. Сольовий розчин А становить 60% солі, а розчин солі В - 80% солі. Скільки кожного розчину потрібно використовувати?

Відповідь

30 мл 80% розчину; 20 мл 60% розчину.

Вправа$\PageIndex{14}$

Хіміку потрібно 2 літри 18% розчину кислоти. Він має два розчини, А і В, щоб змішати разом, щоб утворити розчин. Кислотний розчин А - 10% кислота, а розчин кислоти В - 15% кислоти. Чи може хімік сформувати необхідний 18% розчин кислоти? (Перевірити розрахунком.) Якщо хімік знайде 20% розчин кислоти, скільки доведеться змішувати з 10% -ним розчином, щоб отримати необхідний 2-літровий 18% розчин?

Вправа$\PageIndex{15}$

Хіміку потрібно 3 літри 12% розчину кислоти. У неї є два кислотні розчини, А і В, щоб змішати разом, утворюючи розчин. Кислотний розчин А становить 14% кислоти, а розчин кислоти В - 20% кислоти. Чи може хімік сформувати необхідний 12% розчин? (Перевірити розрахунком.) Якщо хімік знайде 4% розчин кислоти, скільки доведеться змішувати з 14% -ним розчином кислоти, щоб отримати необхідний 3-літровий 12% розчин?

Відповідь

а) не може утворювати 12% розчин;

б)$\dfrac{3}{5}$ літр 4% розчину.

Вправа$\PageIndex{16}$

Студенту хімії потрібно 100 мл 16% -ного розчину кислоти. У нього є флакон з 20% -ним розчином кислоти. Скільки чистої води і скільки 20% розчину потрібно змішати, щоб розвести 20% розчин кислоти до 16% -ного розчину кислоти?

Вправа$\PageIndex{17}$

Студенту-хіміку потрібен 1 літр 78% розчину солі. У неї є пляшка 80% розчину солі. Скільки чистої води і скільки 80% розчину солі потрібно змішати, щоб розвести 80% розчин солі до 78% розчину солі?

Відповідь

25 мл чистої води; 975 мл 80% розчину солі.

Вправа$\PageIndex{18}$

25 мл чистої води; 975 мл 80% розчину солі.

Вправа$\PageIndex{19}$

Дитячий банк містить 78 монет. Монети тільки копійки і нікелі. Якщо вартість монет становить $1,50, скільки з кожної монети є?

Відповідь

18 нікелів; 60 копійок.

Вправи для огляду

Вправа$\PageIndex{20}$

Спростити$\dfrac{x^{n + 6}}{x^2}$

Вправа$\PageIndex{21}$

Знайдіть товар:$(3x - 5)^2$

Відповідь

$9x^2 - 30x + 25$

Вправа$\PageIndex{22}$

Знайдіть різницю:$\dfrac{2x - 1}{x^2 + x - 6} - \dfrac{x + 2}{x^2 + 5x + 6}$

Вправа$\PageIndex{23}$

Використовуйте метод заміщення для вирішення

\ (\ лівий\ {\ begin {масив} {r}
4x - y = 3\\
2x - 5 = 15
\ end {масив}\ вправо.\)

Відповідь

$(0,−3)$

Вправа$\PageIndex{24}$

Використовуйте метод додавання для вирішення

\ (\ ліворуч\ {\ begin {масив} {r}
3x + 4y = -7\\
4x - 5y = 1
\ end {масив}\ вправо.\)