8.10: Ділильні многочлени

Ділення многочлена на мономіал

Наступні приклади ілюструють, як розділити многочлен на мономіал. Процес поділу досить простий і заснований на додаванні раціональних виразів.

$\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a+b}{c}$

Повертаючи це рівняння, ми отримуємо

$\dfrac{a+b}{c} = \dfrac{a}{c} + \dfrac{b}{c}$

Тепер просто$c$ ділимо на$a$, і$c$ на$b$. Це повинно підказати правило.

Ділення многочлена на мономіал

Щоб розділити многочлен на мономіал, розділіть кожен член многочлена на мономіал.

Набір зразків A

Приклад$\PageIndex{1}$

$\dfrac{3x^2 + x - 11}{x}$. Розділіть кожен термін$3x^2 + x - 11$ на$x$.

$\dfrac{3x^2}{x} + \dfrac{x}{x} - \dfrac{11}{x} = 3x + 1 - \dfrac{11}{x}$

Приклад$\PageIndex{2}$

$\dfrac{8x^3 + 4a^2 - 16a + 9}{2a^2}. Divide every term of \(8a^3 + 4a^2 - 16a + 9$по$2a^2$.

Приклад$\PageIndex{3}$

$\dfrac{4b^6 - 9b^4 - 2b + 5}{-4b^2}$. Розділіть кожен термін$4b^6 - 9b^4 - 2b + 5$ на$-4b^2$.

$\dfrac{4b^6}{-4b^2} - \dfrac{9b^4}{-4b^2} - \dfrac{2b}{-4b^2} + \dfrac{5}{-4b^2} = -b^4 + \dfrac{9}{4}b^2 + \dfrac{1}{2b} - \dfrac{5}{4b^2}$

Практика Set A

Виконайте наступні поділи.

Завдання практики$\PageIndex{1}$

$\dfrac{2x^2 + x - 1}{x}$

Відповідь

$2x + 1 - \dfrac{1}{x}$

Завдання практики$\PageIndex{2}$

$\dfrac{3x^3 + 4x^2 + 10x - 4}{x^2}$

Відповідь

$3x + 4 + \dfrac{10}{x} - \dfrac{4}{x^2}$

Завдання практики$\PageIndex{3}$

$\dfrac{a^2b + 3ab^2 + 2b}{ab}$

Відповідь

$a + 3b + \dfrac{2}{a}$

Завдання практики$\PageIndex{4}$

$\dfrac{14x^2y^2 - 7xy}{7xy}$

Відповідь

$2xy−1$

Завдання практики$\PageIndex{5}$

$\dfrac{10m^3n^2 + 15m^2n^3 - 20mn}{-5m}$

Відповідь

$-2m^2n^2 - 3mn^3 + 4n$

Процес поділу

У розділі 8.3 ми вивчали метод зменшення раціональних виразів. Наприклад, ми спостерігали, як зменшити такий вираз, як

$\dfrac{x^2 - 2x - 8}{x^2 - 3x - 4}$

Наш метод полягав у тому, щоб розрахувати як чисельник, так і знаменник, а потім розділити загальні фактори.

$\dfrac{(x-4)(x+2)}{(x-4)(x+1)}$

$\dfrac{\cancel{(x-4)}(x+2)}{\cancel{(x-4)}(x+1)}$

$\dfrac{x+2}{x+1}$

Коли чисельник та знаменник не мають спільних факторів, поділ все одно може відбуватися, але процес трохи більше задіяний, ніж просто факторинг. Спосіб ділення одного многочлена на інший набагато такий же, як і при діленні одного числа на інше. Для початку розглянемо етапи ділення чисел.

$\dfrac{35}{8}$. Ми маємо розділити 35 на 8.

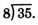Ми намагаємося 4, так як 32 ділиться на 8 дорівнює 4.

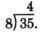Помножте 4 і 8

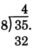Відняти 32 з 35

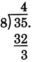Так як залишок 3 менше дільника 8, ми робимо з діленням 32.

$4\dfrac{3}{8}$. Коефіцієнт виражається у вигляді мішаного числа.

Процес полягав у поділі, множенні та відніманні.

Огляд віднімання многочленів

Дуже важливим етапом в процесі ділення одного многочлена на інший є віднімання многочленів. Розглянемо процес віднімання, спостерігаючи кілька прикладів.

1. Відняти$x -2$ від$x-5$; тобто знайти$(x-5) - (x-2)$.

Так як$x-2$ передує знак мінус, зніміть дужки, поміняйте знак кожного члена, потім додайте.

\ (\ begin {масив} {Flushleft}
x-5 & x-5\\
- (x-2) &&-x+2
\\ текст {_______} & = &\ текст {_______}\\
&&-3
\ кінець {масив}\)

Результат$-3$

2. Відняти$x^3 + 3x^2$ від$x^3 + 4x^2 + x - 1$.

Так як$x^3 + 3x^2$ передує знак мінус, зніміть дужки, поміняйте знак кожного члена, потім додайте.

\ (\ почати {масив} {Flushleft}
x^3 + 4x^2 + x - 1 &&x ^ 3 + 4x^2 + x
- 1\\ - (x^3 + 3x^2) &-x^3 - 3x^2
\\ текст {_______________}\\ текст {_______________}\
&&x^2 + х 1
\\ кінець масиву}\)

Результат$x^2 + x - 1$

3. Відняти$x^2 + 3x$ від$x^2 + 1$

Ми можемо писати$x^2 + 1$ як$x^2 + 0x + 1$.

\ (\ begin {масив} {Flushleft}
x^2 + 1 &x ^ 2+ 0x + 1 &x ^ 2 + 0x + 1\\
- (x^2+ 3x) && - (x^2+ 3x) &-x^2 - 3x
\\ текст {____________} & =\ текст {____________} & =\ текст {____________}
&&& -3x + 1
\ end {масив}\)

Ділення многочлена на многочлен

Зараз ми розглянемо кілька прикладів ділення одного многочлена на інший. Процес такий же, як процес, який використовується з цілими числами: ділити, помножити, віднімати, ділити, помножити, віднімати,...

Ділення, множення та віднімання відбуваються по одному члену за раз. Процес завершується, коли залишок полінома має менший ступінь, ніж поліноміальний дільник.

Набір зразків B

Виконуємо поділ.

Приклад$\PageIndex{4}$

$\dfrac{x-5}{x-2}$. Ми повинні розділити$x-5$ на$x-2$.

$1 - \dfrac{3}{x-2}$

Таким чином,

$\dfrac{x-5}{x-2} = 1 - \dfrac{3}{x-2}$

Приклад$\PageIndex{5}$

$\dfrac{x^3 + 4x^2 + x - 1}{x + 3}$. Ми повинні розділити$x^3 + 4x^2 + x - 1$ на$x + 3$.

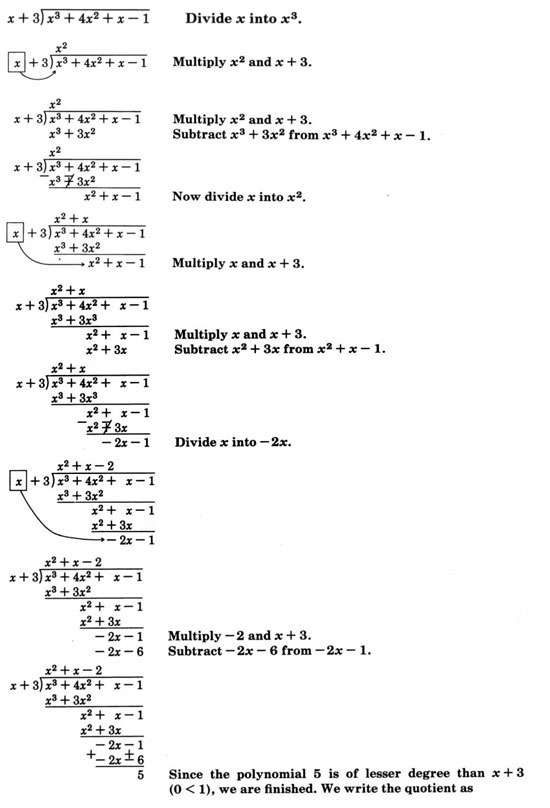
$x^2 + x - 2 + \dfrac{5}{x+3}$

Таким чином,

$\dfrac{x^3 + 4x^2 + x - 1}{x + 3} = x^2 + x - 2 + \dfrac{5}{x+3}$

Практика Set B

Виконайте наступні поділи.

Завдання практики$\PageIndex{6}$

$\dfrac{x+6}{x-1}$

Відповідь

$1 + \dfrac{7}{x-1}$

Завдання практики$\PageIndex{7}$

$\dfrac{x^2 + 2x + 5}{x + 3}$

Відповідь

$x - 1 + \dfrac{8}{x+3}$

Завдання практики$\PageIndex{8}$

$\dfrac{x^3 + x^2 - x - 2}{x + 8}$

Відповідь

$x^2 - 7x + 55 - \dfrac{442}{x+8}$

Завдання практики$\PageIndex{9}$

$\dfrac{x^3 + x^2 - 3x + 1}{x^2 + 4x - 5}$

Відповідь

$x - 3 + \dfrac{14x - 14}{x^2 + 4x - 5} = x - 3 + \dfrac{14}{x+5}$

Набір зразків C

Приклад$\PageIndex{6}$

Розділити$2x^3 - 4x + 1$ на$x + 6$

$\dfrac{2x^3 - 4x + 1}{x + 6}$Зверніть увагу, що$x^2$ термін в чисельнику відсутній. Ми можемо уникнути будь-якої плутанини, написавши

$\dfrac{2x^3 + 0x^2 - 4x + 1}{x+6}$Ділити, помножити і відняти.

$\dfrac{2x^3 - 4x + 1}{x + 6} = 2x^3 - 12x + 68 - \dfrac{407}{x + 6}$

Практика Set C

Виконайте наступні поділи.

Завдання практики$\PageIndex{10}$

$\dfrac{x^2 - 3}{x+2}$

Відповідь

$x - 2 + \dfrac{1}{x+2}$

Завдання практики$\PageIndex{11}$

$\dfrac{4x^2 - 1}{x-3}$

Відповідь

$4x + 12 + \dfrac{35}{x-3}$

Завдання практики$\PageIndex{12}$

$\dfrac{x^3 + 2x + 2}{x-2}$

Відповідь

$x^2 + 2x + 6 + \dfrac{14}{x-2}$

Завдання практики$\PageIndex{13}$

$\dfrac{6x^3 + 5x^2 - 1}{2x + 3}$

Відповідь

$3x^2 - 2x + 3 - \dfrac{10}{2x + 3}$

вправи

Для наступних завдань виконайте поділи.

Вправа$\PageIndex{1}$

$\dfrac{6a + 12}{2}$

Відповідь

$3a+6$

Вправа$\PageIndex{2}$

$\dfrac{12b - 6}{3}$

Вправа$\PageIndex{3}$

$\dfrac{8y - 4}{-4}$

Відповідь

$−2y+1$

Вправа$\PageIndex{4}$

$\dfrac{21a - 9}{-3}$

Вправа$\PageIndex{5}$

$\dfrac{3x^2 - 6x}{-3}$

Відповідь

$−x(x−2)$

Вправа$\PageIndex{6}$

$\dfrac{4y^2 - 2y}{2y}$

Вправа$\PageIndex{7}$

$\dfrac{9a^2 + 3a}{2a}$

Відповідь

$3a+1$

Вправа$\PageIndex{8}$

$\dfrac{20x^2 + 10x}{5x}$

Вправа$\PageIndex{9}$

$\dfrac{6x^3 + 2x^2 + 8x}{2x}$

Відповідь

$3x^2 + x + 4$

Вправа$\PageIndex{10}$

$\dfrac{26y^3 + 13y^2 + 39y}{13y}$

Вправа$\PageIndex{11}$

$\dfrac{a^2b^2 + 4a^2b + 6ab^2 - 10ab}{ab}$

Відповідь

$ab+4a+6b−10$

Вправа$\PageIndex{12}$

$\dfrac{7x^3y + 8x^2y^3 + 3xy^4 - 4xy}{xy}$

Вправа$\PageIndex{13}$

$\dfrac{5x^3y^3 - 15x^2y^2 + 20xy}{-5xy}$

Відповідь

$-x^2y^2 + 3xy - 4$

Вправа$\PageIndex{14}$

$\dfrac{4a^2b^3 - 8ab^4 + 12ab^2}{-2ab^2}$

Вправа$\PageIndex{15}$

$\dfrac{6a^2y^2 + 12a^2y + 18a^2}{24a^2}$

Відповідь

$\dfrac{1}{4}y^2 + \dfrac{1}{2}y + \dfrac{3}{4}$

Вправа$\PageIndex{16}$

$\dfrac{3c^3y^3 + 99c^3y^4 - 12c^3y^5}{3x^3y^3}$

Вправа$\PageIndex{17}$

$\dfrac{16ax^2 - 20ax^3 + 24ax^4}{6a^4}$

Відповідь

$\dfrac{8x^2 - 10x^3 + 12x^4}{3a^3}$або$\dfrac{12x^4 - 10x^3 + 8x^2}{3a^2}$

Вправа$\PageIndex{18}$

$\dfrac{21ay^3 - 18ay^2 - 15ay}{6ay^2}$

Вправа$\PageIndex{19}$

$\dfrac{-14b^2c^2 + 21b^3 - 28c^3}{-7a^2c^3}$

Відповідь

$\dfrac{2b^2 - 3b^3c + 4c}{a^2c}$

Вправа$\PageIndex{20}$

$\dfrac{-30a^2b^4 - 35a^2b^3 - 25a^2}{-5b^3}$

Вправа$\PageIndex{21}$

$\dfrac{x+6}{x-2}$

Відповідь

$1 + \dfrac{8}{x-2}$

Вправа$\PageIndex{22}$

$\dfrac{y + 7}{y + 1}$

Вправа$\PageIndex{23}$

$\dfrac{x^2 - x + 4}{x + 2}$

Відповідь

$x - 3 + \dfrac{10}{x+2}$

Вправа$\PageIndex{24}$

$\dfrac{x^2 + 2x - 1}{x + 1}$

Вправа$\PageIndex{25}$

$\dfrac{x^2 - x + 3}{x + 1}$

Відповідь

$x - 2 + \dfrac{5}{x + 1}$

Вправа$\PageIndex{26}$

$\dfrac{x^2 + 5x + 5}{x + 5}$

Вправа$\PageIndex{27}$

$\dfrac{x^2 - 2}{x + 1}$

Відповідь

$x - 1 - \dfrac{1}{x+1}$

Вправа$\PageIndex{28}$

$\dfrac{a^2 - 6}{a + 2}$

Вправа$\PageIndex{29}$

$\dfrac{y^2 + 4}{y + 2}$

Відповідь

$y - 2 + \dfrac{8}{y + 2}$

Вправа$\PageIndex{30}$

$\dfrac{x^2 + 36}{x + 6}$

Вправа$\PageIndex{31}$

$\dfrac{x^3 - 1}{x + 1}$

Відповідь

$x^2 - x + 1 - \dfrac{2}{x + 1}$

Вправа$\PageIndex{32}$

$\dfrac{a^3 - 8}{a + 2}$

Вправа$\PageIndex{33}$

$\dfrac{x^3 + 3x^2 + x - 2}{x-2}$

Відповідь

$x^2 + 5x + 11 + \dfrac{20}{x-2}$

Вправа$\PageIndex{34}$

$\dfrac{a^3 + 2a^2 - a + 1}{a - 3}$

Вправа$\PageIndex{35}$

$\dfrac{x^3 + 2x + 1}{x - 3}$

Вправа$\PageIndex{36}$

$\dfrac{y^3 + 2y^2 + 4}{y + 2}$

Відповідь

$y^2 + y - 2 + \dfrac{8}{y + 2}$

Вправа$\PageIndex{37}$

$\dfrac{y^3 + 5y^2 - 3}{y - 1}$

Вправа$\PageIndex{38}$

$\dfrac{x^3 + 3x^2}{x + 3}$

Відповідь

$x^2$

Вправа$\PageIndex{39}$

$\dfrac{a^2 + 2a}{a + 2}$

Вправа$\PageIndex{40}$

$\dfrac{x^2 - x - 6}{x^2 - 2x - 3}$

Відповідь

$1 + \dfrac{1}{x + 1}$

Вправа$\PageIndex{41}$

$\dfrac{a^2 + 5a + 4}{a^2 - a - 2}$

Вправа$\PageIndex{42}$

$\dfrac{2y^2 + 5y + 3}{y^2 - 3y - 4}$

Відповідь

$2 + \dfrac{11}{y-4}$

Вправа$\PageIndex{43}$

$\dfrac{3a^2 + 4a + 2}{3a + 4}$

Вправа$\PageIndex{44}$

$\dfrac{6x^2 + 8x - 1}{3x + 4}$

Відповідь

$2x - \dfrac{1}{3x + 4}$

Вправа$\PageIndex{45}$

$\dfrac{20y^2 + 15y - 4}{4y + 3}$

Вправа$\PageIndex{46}$

$\dfrac{4x^3 + 4x^2 - 3x - 2}{2x - 1}$

Відповідь

$2x^2 + 3x - \dfrac{2}{2x - 1}$

Вправа$\PageIndex{47}$

$\dfrac{9a^3 - 18a^2 8a - 1}{3a - 2}$

Вправа$\PageIndex{48}$

$\dfrac{4x^4 - 4x^3 + 2x^2 - 2x - 1}{x-1}$

Відповідь

$4x^3 + 2x - \dfrac{1}{x-1}$

Вправа$\PageIndex{49}$

$\dfrac{3y^4 + 9y^3 - 2y^2 - 6y + 4}{y + 3}$

Вправа$\PageIndex{50}$

$\dfrac{3y^2 + 3y + 5}{y^2 + y + 1}$

Відповідь

$3 + \dfrac{2}{y^2 + y + 1}$

Вправа$\PageIndex{51}$

$\dfrac{2a^2 + 4a + 1}{a^2 + 2a + 3}$

Вправа$\PageIndex{52}$

$\dfrac{8z^6 - 4z^5 - 8z^4 + 8z^3 + 3z^2 - 14z}{2z - 3}$

Відповідь

$4z^5 + 4z^4 + 2z^3 + 7z^2 + 12z + 11 + \dfrac{33}{2z - 3}$

Вправа$\PageIndex{53}$

$\dfrac{9 a^{7}+15 a^{6}+4 a^{5}-3 a^{4}-a^{3}+12 a^{2}+a-5}{3 a+1}$

Вправа$\PageIndex{54}$

$(2x^5 + 5x^4 -1) \div (2x + 5)$

Відповідь

$x^4 - \dfrac{1}{2x + 5}$

Вправа$\PageIndex{55}$

$(6a^4 - 2a^3 - 3a^2 + a + 4) \div (3a - 1)$

Вправи для огляду

Вправа$\PageIndex{56}$

Знайдіть товар. $\dfrac{x^2 + 2x - 8}{x^2 - 9} \cdot \dfrac{2x + 6}{4x - 8}$

Відповідь

$\dfrac{x + 4}{2(x-3)}$

Вправа$\PageIndex{57}$

Знайти суму. $\dfrac{x-7}{x + 5} + \dfrac{x + 4}{x - 2}$

Вправа$\PageIndex{58}$

Розв'яжіть рівняння$\dfrac{1}{x + 3} + \dfrac{1}{x - 3} = \dfrac{1}{x^2 - 9}$

Відповідь

$x = \dfrac{1}{2}$

Вправа$\PageIndex{59}$

Коли одне і те ж число віднімається як з чисельника, так і від знаменника$dfrac{3}{10}$, результат буде$\dfrac{1}{8}$. Що таке число, яке віднімається?

Вправа$\PageIndex{60}$

Спростити$\dfrac{\frac{1}{x+5}}{\frac{4}{x^{2}-25}}$

Відповідь

$\dfrac{x-5}{4}$