21.3: Геометричні конструкції

Last updated
Save as PDF

Page ID: 64228

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У Стародавній Греції ставилися три класичні проблеми. Ці проблеми мають геометричний характер і передбачають прямолінійно-компасні конструкції з того, що зараз є геометрією середньої школи; тобто нам дозволено використовувати лише прямокутник і компас для їх вирішення. Проблеми можна констатувати наступним чином.

Враховуючи довільний кут, чи можна трисекти кут на три рівні підкути, використовуючи лише прямокутник та компас?
З огляду на довільне коло, чи можна побудувати квадрат з однаковою площею, використовуючи лише прямокутник і циркуль?
За умови куба, чи можна побудувати ребро іншого куба, що має вдвічі більший об'єм оригіналу? Знову ж таки, нам дозволяється використовувати лише прямий край і компас для виконання будівництва.

Після того, як математиків спантеличували більше двох тисяч років, кожна з цих конструкцій нарешті виявилася неможливою. Ми будемо використовувати теорію полів, щоб надати доказ того, що рішень не існує. Досить примітно, що давно шукане рішення кожної з цих трьох геометричних задач прийшло з абстрактної алгебри.

Для початку визначимося більш конкретно, що ми маємо на увазі під прямокутником і компасом, а також розглянемо природу цих проблем в трохи більшій глибині. Почнемо з того, що прямолінійка - це не лінійка. Ми не можемо виміряти довільні довжини з прямолінійним краєм. Це всього лише інструмент для малювання лінії через дві точки. Твердження про те, що трисекція довільного кута неможлива, означає, що існує хоча б один кут, який неможливо перетнути за допомогою прямолінійно-циркулярної конструкції. Звичайно, можна перетинати кут в особливих випадках. Ми можемо побудувати$30^\circ$ кут; отже, можна перетнути$90^\circ$ кут. Однак покажемо, що побудувати$20^\circ$ кут неможливо. Тому ми не можемо перетинати$60^\circ$ кут.

Побудовані числа

$\alpha$Дійсне число є конструктивним, якщо ми можемо побудувати відрізок лінії довжини$| \alpha |$ в скінченній кількості кроків від відрізка одиниці довжини за допомогою прямолінійного краю і компаса.

Теорема$21.37$

Безліч всіх конструктивних дійсних чисел утворює підполе$F$ поля дійсних чисел.

Доказ: $\beta$Дозволяти$\alpha$ і бути конструктивними числами. Ми повинні показати, що$\alpha + \beta\text{,}$$\alpha - \beta\text{,}$$\alpha \beta\text{,}$ і$\alpha / \beta$ ($\beta \neq 0$) також є конструктивними числами. Можна припустити, що обидва$\alpha$ і$\beta$ є позитивними з$\alpha \gt \beta\text{.}$ Цілком очевидно, як побудувати$\alpha + \beta$ і$\alpha - \beta\text{.}$ Щоб знайти відрізок лінії з довжиною,$\alpha \beta\text{,}$ ми припускаємо, що$\beta \gt 1$ і побудувати трикутник на малюнку$21.38$ такий, що трикутники$\triangle ABC$ і $\triangle ADE$схожі. Оскільки$\alpha / 1 = x / \beta\text{,}$ відрізок лінії$x$ має довжину$\alpha \beta\text{.}$ Аналогічна конструкція може бути зроблена, якщо$\beta \lt 1\text{.}$ Ми залишимо це як вправу, щоб показати, що той самий трикутник може бути використаний для побудови$\alpha / \beta$ для$\beta \neq 0\text{.}$

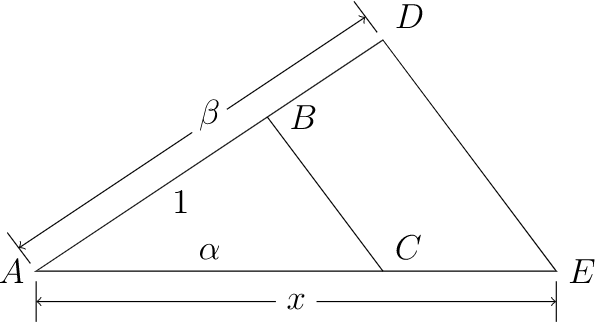
$clipboard_eeed5c17bb29eea88db6fa03dae25709c.png$

$Figure \text { } 21.38.$конструювання виробів

Лемма$21.39$

Якщо$\alpha$ є конструктивним числом, то$\sqrt{\alpha}$ є конструктивним числом.

Доказ: На$21.40$ малюнку трикутники$\triangle ABD\text{,}$$\triangle BCD\text{,}$ і$\triangle ABC$ схожі; отже,$1 /x = x / \alpha\text{,}$ або$x^2 = \alpha\text{.}$

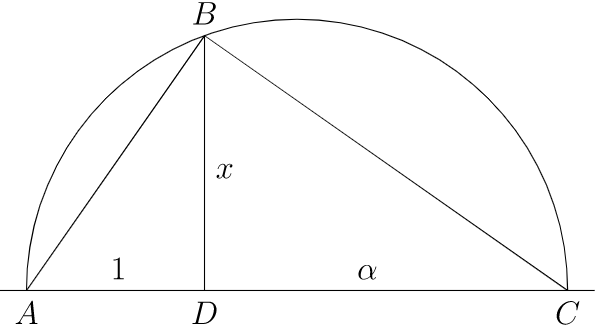
$clipboard_ec73c4c9dbab4977931645adcf26aa5a8.png$

$Figure \text { } 21.40.$спорудження коренів

За теоремою$21.37$, ми можемо знайти в площині будь-яку точку,$P =( p, q)$ яка має раціональні координати$p$ і$q\text{.}$ Ми повинні знати, які ще точки можна побудувати за допомогою компаса і випрямляти від точок з раціональними координатами.

Лемма$21.41$

$F$Дозволяти бути підполем${\mathbb R}\text{.}$

Якщо рядок містить дві точки,$F\text{,}$ то вона має рівняння$a x + by + c = 0\text{,}$ де$a\text{,}$$b\text{,}$ і$c$ знаходяться в$F\text{.}$
Якщо коло має центр у точці з координатами в$F$ і радіусом, який також знаходиться в,$F\text{,}$ то воно має рівняння$x^2 + y^2 + d x + e y + f = 0\text{,}$ де$d\text{,}$$e\text{,}$ і$f$ знаходяться в$F\text{.}$

Доказ

Дозволяти$(x_1, y_1)$ і$(x_2, y_2)$ бути точки на лінії, координати якої знаходяться в$F\text{.}$ Якщо$x_1 = x_2\text{,}$ тоді рівняння прямої через дві точки,$x - x_1 = 0\text{,}$ яка має вигляд$a x + by + c = 0\text{.}$ Якщо$x_1 \neq x_2\text{,}$ тоді рівняння прямої через дві точки задається

\[ y - y_1 = \left( \frac{y_2 - y_1}{x_2 - x_1} \right) (x - x_1)\text{,} \nonumber \]

які також можна поставити в належний вигляд.

Щоб довести другу частину леми, припустимо, що$(x_1, y_1)$ це центр кола радіуса$r\text{.}$ Тоді коло має рівняння

\[ (x - x_1)^2 + (y - y_1)^2 - r^2 = 0\text{.} \nonumber \]

Це рівняння легко можна вивести у відповідну форму.

Починаючи з поля конструктивних чисел,$F\text{,}$ ми маємо три можливі способи побудови додаткових точок${\mathbb R}$ у циркулі та прямолінійці.

Щоб знайти можливі нові точки,${\mathbb R}\text{,}$ ми можемо взяти перетин двох ліній, кожна з яких проходить через дві відомі точки з координатами в$F\text{.}$
Перетин лінії, яка проходить через дві точки, які мають координати в$F$ і коло, центр якого має координати в$F$ з радіусом довжини в$F$ дасть нові точки в${\mathbb R}\text{.}$
Ми можемо отримати нові точки${\mathbb R}$, перетинаючи два кола, центри яких мають координати в$F$ і радіуси яких мають довжину в$F\text{.}$

Перший випадок не дає нових точок,${\mathbb R}\text{,}$ оскільки розв'язання двох рівнянь виду,$a x + by + c = 0$ що мають коефіцієнти в завжди$F$ буде в$F\text{.}$ третьому випадку можна звести до другого випадку. Нехай

\ почати {збирати*} x^2 + y^2 + d_1 х + e_1 y + f_1 = 0\\ x^2 + y^2 + д_2 х + e_2 y + f_2 y + f_2 = 0\ end {збирати*}

бути рівняння двох кіл, де$d_i\text{,}$$e_i\text{,}$ і$f_i$ знаходяться в$F$ для$i = 1, 2\text{.}$ Ці кола мають таке ж перетин, як і коло

\[ x^2 + y^2 + d_1 x +e_1 x + f_1 = 0 \nonumber \]

і лінія

\[ (d_1 - d_2) x + b(e_2 - e_1)y + (f_2 - f_1) = 0\text{.} \nonumber \]

Останнє рівняння - це хорда, що проходить через точки перетину двох кіл. Значить, перетин двох кіл можна звести до випадку перетину прямої з колом.

Розглядаючи випадок перетину прямої і окружності, треба визначити характер розв'язків рівнянь

\ begin {вирівнювати*} а х + за допомогою + c & = 0\\ x^2 + y^2 + d x + e y + f & = 0\ текст {.} \ end {вирівнювати*}

Якщо виключити$y$ з цих рівнянь, то отримаємо рівняння виду$Ax^2 + B x + C = 0\text{,}$ де$A\text{,}$$B\text{,}$ і$C$ знаходяться в$F\text{.}$$x$ Координата точок перетину задається

\[ x = \frac{- B \pm \sqrt{B^2 - 4 A C} }{2 A} \nonumber \]

і знаходиться$F( \sqrt{\alpha}\, )\text{,}$ там, де$\alpha = B^2 - 4 A C \gt 0\text{.}$ Ми довели наступну лему.

Лемма$21.42$

$F$Дозволяти поле з конструктивних чисел. Тоді точки, що визначаються перетинами ліній і кіл в$F$ лежать в полі$F( \sqrt{\alpha}\, )$ для деяких$\alpha$ в$F\text{.}$

Теорема$21.43$

Справжнє число$\alpha$ є конструктивним числом тоді і тільки тоді, коли існує послідовність полів.

\[ {\mathbb Q} = F_0 \subset F_1 \subset \cdots \subset F_k \nonumber \]

такі, що$F_i = F_{i-1}( \sqrt{ \alpha_i}\, )$ з$\alpha_i \in F_i$ і$\alpha \in F_k\text{.}$ Зокрема, існує ціле число$k \gt 0$ таке, що$[{\mathbb Q}(\alpha) : {\mathbb Q} ] = 2^k\text{.}$

Доказ: Існування і$F_i$ те є прямим наслідком Лемми 21.42 і того факту, що$\alpha_i$

\[ [F_k: {\mathbb Q}] = [F_k : F_{k - 1}][F_{k - 1} : F_{k - 2}] \cdots [F_1: {\mathbb Q} ] = 2^k\text{.} \nonumber \]

Слідство$21.44$

Поле всіх конструктивних чисел є алгебраїчним розширенням\ ({\ mathbb Q}\ text { . }\

Як ми бачимо з поля конструктивних чисел, не кожне алгебраїчне розширення поля є кінцевим розширенням.

Подвоєння куба і квадратичне коло

Тепер ми готові досліджувати класичні задачі подвоєння куба і квадратизації кола. Ми можемо використовувати поле конструктивних чисел, щоб точно показати, коли конкретна геометрична конструкція може бути виконана.

Подвоїти куб неможливо.

З огляду на ребро куба, неможливо побудувати за допомогою прямокутника і циркуля ребро куба, що має подвоєний обсяг вихідного куба. Нехай оригінальний куб має ребро довжини$1$ і, отже, об'єм$1\text{.}$ Якби ми могли побудувати куб, що має об'єм$2\text{,}$ тоді цей новий куб буде мати ребро довжини$\sqrt[3]{2}\text{.}$ Однак,$\sqrt[3]{2}$ є нулем від незведеного многочлена$x^3 -2$,${\mathbb Q}\text{;}$ отже,

\[ [{\mathbb Q}(\sqrt[3]{2}\, ) : {\mathbb Q}] = 3 \nonumber \]

Це неможливо, оскільки не$3$ є силою$2\text{.}$

Квадратування кола.

Припустимо, що у нас є радіус$1\text{.}$ Площа кола,$\pi\text{;}$ отже, ми повинні бути в змозі побудувати квадрат зі стороною$\sqrt{\pi}\text{.}$ Це неможливо, оскільки$\pi$ і, отже$\sqrt{\pi}$, обидва трансцендентні. Тому, використовуючи прямокутник і циркуль, не представляється можливим побудувати квадрат з тією ж площею, що і коло.

Перетин кута

Перетин довільного кута неможливо. Ми покажемо, що побудувати$20^\circ$ кут неможливо. Отже,$60^{\circ}$ кут не може бути пересічений. Для початку потрібно обчислити формулу потрійного кута для косинуса:

\ begin {align*}\ cos 3\ тета & =\ cos (2\ тета +\ тета)\\ & =\ cos 2\ theta\ cos\ theta\ theta -\ sin\ sin\ sin\ тета\\ & = (2\ cos^2\ тета - 2\ sin^2\ theta - 2\ sin^2\ theta\ cos\ cos\ theta\\ & = (2\ cos ^ 2\ theta - 1 cos)\\ тета - 2 (1-\ cos^2\ тета)\ cos\ тета\\ & = 4\ cos^3\ тета - 3\ cos\ тета\ текст {.} \ end {вирівнювати*}

Кут$\theta$ може бути побудований, якщо і тільки в тому випадку, якщо$\alpha = \cos \theta$ є конструктивним. Нехай$\theta = 20^{\circ}\text{.}$ Тоді$\cos 3 \theta = \cos 60^\circ = 1/2\text{.}$ За формулою потрійного кута для косинуса,

\[ 4 \alpha^3 - 3 \alpha = \frac{1}{2}\text{.} \nonumber \]

Отже,$\alpha$ є нулем$8 x^3 - 6 x -1\text{.}$ Цей многочлен не має чинників${\mathbb Z}[x]\text{,}$ і, отже, є нескоротним над${\mathbb Q}[x]\text{.}$ Таким чином,$[{\mathbb Q}( \alpha ) : {\mathbb Q }] = 3\text{.}$ отже,$\alpha$ не може бути конструктивним числом.

Історична записка

Алгебраїчна теорія чисел використовує інструменти алгебри для вирішення задач теорії чисел. Сучасна алгебраїчна теорія чисел почалася з П'єра де Ферма (1601—1665). Звичайно, ми можемо знайти багато позитивних цілих чисел, які задовольняють рівнянню$x^2 + y^2 = z^2\text{;}$ Ферма, припустив, що рівняння не$x^n + y^n = z^n$ має позитивних цілих розв'язків для$n \geq 3\text{.}$ Він заявив на порах своєї копії латинського перекладу Арифметики Діофанта, що він знайшов чудове доказ цієї теореми, але що край книги був занадто вузьким, щоб її містити. Спираючись на роботу інших математиків, саме Ендрю Уайлз нарешті вдалося довести останню теорему Ферма в 1990-х роках. Про досягнення Уайлса повідомили на першій сторінці газети New York Times.

Спроби довести останню теорему Ферма призвели до важливого внеску в алгебраїчну теорію чисел таких відомих математиків, як Леонхард Ейлер (1707—1783). Значних успіхів у розумінні останньої теореми Ферма зробив Ернст Куммер (1810—1893). Учень Куммера Леопольд Кронекер (1823—1891) став одним з провідних алгебраїстів дев'ятнадцятого століття. Теорія ідеалів Кронекера та його вивчення алгебраїчної теорії чисел додали багато в розуміння полів.

Девід Гільберт (1862—1943) та Герман Мінковський (1864—1909) були серед математиків, які вели шлях у цій темі на початку ХХ століття. Гільберт і Мінковський обидва були математиками в Геттінгенському університеті в Німеччині. Геттінген був справді одним з найважливіших центрів математичних досліджень протягом останніх двох століть. Велика кількість виняткових математиків, які навчалися там, включали Гаусса, Діріхле, Рімана, Дедекінда, Нетера та Вейля.

Андре Вайль відповів на запитання з теорії чисел, використовуючи алгебраїчну геометрію, область математики, яка вивчає геометрію шляхом вивчення комутативних кілець. Приблизно з 1955 по 1970 рік Олександр Гротендік домінував в області алгебраїчної геометрії. П'єр Делін, студент Гротендіка, вирішив кілька теоретико-числових домислів Вейля. Одним з останніх внесків до алгебри та теорії чисел є доказ Герда Фальтінга гіпотези Морделла-Вейля. Ця здогадка Морделла і Вейля по суті говорить про те, що певні поліноми$p(x, y)$ в${\mathbb Z}[x,y]$ мають лише кінцеве число інтегральних розв'язків.